适用于宽带宽输入的TIADC时间误差校准算法
2021-09-30张宇航孙康康万祝娟尹勇生
张宇航, 孙康康, 李 琨, 万祝娟, 尹勇生
(1.合肥工业大学 微电子设计研究所,安徽 合肥 230601; 2.合肥工业大学 教育部IC设计网上合作研究中心,安徽 合肥 230601)
在通信系统,宽带卫星接收机、有线电视调谐器和软件定义无线电等设备都对模数转换器(analog-to-digital converters,ADC)的采样率、分辨率和低功耗等性能有着越来越高的要求[1]。时间交织模数转换器(time-interleaved ADC,TIADC)通过将几个转换速度慢但分辨率高的ADC并行组合,再将各ADC的数据复合输出即可实现提高量化速度的目的,TIADC工作原理如图1所示。图1中:S/H表示采样保持电路;Max表示复合模块。然而,这种并行的ADC复合工作后又会产生相应的通道失配误差,包括失调失配误差、增益失配误差和时间失配误差。失配误差的产生显著降低TIADC的信噪比(signal-to-noise ratio,SNR)和无杂散动态范围(spurious-free dynamic range,SFDR),影响ADC的性能。因时序失配对TIADC性能的影响随输入频率的增加而增大,而失调失配与增益失配的影响则与输入信号的频率无关[2]。基于此,本文着重解决时序失配问题。

图1 TIADC原理
传统TIADC中的时序失配可以通过使用模拟/数字混合信号校准技术来进行误差的校准[3-5]。但由于工艺的影响,模拟校准的方法限制了整个ADC的校准效果,因此全数字化校准技术成为当前主流的校准方式。目前集中在全数字域的大多数校准算法都将输入信号的带宽限制在奈奎斯特频域内[6-7],即位于第一奈奎斯特范围内。为了实现宽带宽输入的TIADC时间失配误差校准,文献[8]提出利用希尔伯特滤波器可以解决任意奈奎斯特频域内的校准问题,但是要用到几十阶的乘法器,资源消耗很大;文献[9]提出了一种利用一个低阶滤波器以判断输入信号频率所属频带,再根据频带调整校准方向的校准方法,这种方式过程繁琐,不利于硬件实现;文献[10]提出一种复合后求导和复合前求导相与来判断校准符号的方法以提升校准效果,这样虽然能取得较好的校准效果,但是却会使算法多出一个Mux以及需要一个工作速度较快的除法器,进而增加了算法的复杂度以及电路的功耗。
针对上述问题,本文提出了一种适用于宽带宽输入的TIADC时间失配误差校准算法。误差提取采用一种带有符号判断的相邻通道相乘互相关误差提取算法,结构简单且易于实现;误差补偿模块使用改进的泰勒补偿算法,硬件资源消耗较小。校准结果表明,本文方法能够以较小的硬件资源消耗实现宽带宽输入的TIADC时间失配误差校准。
1 时间失配误差校准算法
本文使用全数字化的校准技术来对TIADC的时间失配误差进行校准。算法由误差提取模块和误差补偿模块组成闭环自适应结构,能够实时进行误差校准。本文的校准算法整体框图如图2所示。

图2 校准算法系统框图
图2中,模拟输入信号x(t)经过采样保持电路S/H后,由各通道子ADC转换为含有误差信号的输出y0[k]、y1[k]、y2[k]、y3[k]。经过误差补偿后由Mux复合模块复合后输出。
1.1 基于通道相乘互相关的误差提取
本文的误差提取模块采用基于相邻通道相乘互相关原理的误差提取算法[9],引入误差符号判断模块实现任意输入带宽的时间误差提取,其具体原理如下。
若输入信号为正弦信号,针对时间误差的提取,假设系统不存在失调和增益失配误差,则TIADC的采样输出可以表示为:
ym[k]=Asin[ωin(kM+m+Δtm)+β]
(1)
其中:ωin=2πfin/fs,fin为输入频率,fs为采样频率;M为TIADC通道总数;Δtm为第m通道的时序偏移误差;A为各通道增益;β为初始相位。此时相邻两通道乘积的输出为:
Cm+1,m[k]=ym+1[k]ym[k]=
Δtm+Δtm+1)+2β]
(2)
设采样点数为N个,计算Cm+1,m[k]期望值,当N足够大时,Cm+1,m[k]的期望值为:
E[Cm+1,m[k]]=(1/2)A2cos[ωin(1+Δtm+1-Δtm)]
(3)
同理Cm,m-1[k]的期望值为:
E[Cm,m-1[k]]=(1/2)A2cos[ωin(1+Δtm-Δtm-1)]
(4)
当第m-1个通道ADC和第m+1个通道ADC的时间误差为0,第m个通道ADC时间误差为Δtm时,2个期望绝对值的差可以表示为:
Γm=|E[Cm+1,m[k]]|-|E[Cm,m-1[k]]|=

(5)
由(5)式可知,Γm为时间误差Δtm的函数。因此可以让Γm通过一个最小均方(least mean square,LMS)算法自适应滤波器结构与后面的补偿模块共同构成一个反馈迭代模式,通过让其不断迭代调整自适应滤波器的系数,最终迭代出误差值Δtm,其工作原理如图3所示。

图3 第m通道误差提取原理图
图3中:Acc、Avg为指数平均器;LMS为最小均方算法自适应滤波器。
1.2 误差符号判断
在实际的校准过程中发现,随着输入信号频率的变化,在采样和提取的过程中时间误差的方向会发生相应变化[11]。为实现正确补偿,图3中加法器的正、负号随输入频率的变化需要作出相应的改变,通过大量实验分析,可以得到时间失配误差的符号变化规律如下。
首先在采样过程中,对于不同的输入信号频率fin,经过采样后的第m通道ADC的时间误差Δtm′与未经采样的第m通道ADC的时间误差Δtm的关系如下:

以四通道TIADC为例,通过分析得到,第二子奈奎斯特与第一子奈奎斯特相反,输入频率继续增大后,误差估计值的符号变化是以第一、第二子奈奎斯特为周期的变化。用“+”表示采样前、后时间误差的方向相同,“-”表示采样前后时间误差的方向相反。采样过程中输入信号频率与误差符号的关系见表1所列。

表1 采样过程中输入信号频率与误差符号的关系
其次在误差提取的过程中,由于Δtm≪1,将ωin=πfin/(2fsub)代入(5)式可得:
(6)
当(fin/fsub)∈[(4n,4n+1)∪(4n+2,4n+3)]时,n∈Z,由(6)式可知,Γm与误差Δtm同向,提取的误差方向没有发生错误,在整个校准过程中可以得到有效的提取和补偿。
当(fin/fsub)∈[(4n+1,4n+2)∪(4n+3,4n+4)]时,n∈Z,由(6)式可知,Γm与误差Δtm方向相反,即得到的误差为-Δtm,提取的误差方向发生错误,这会导致提取过程出现错误,进而无法进行有效的补偿,导致迭代无法收敛。
由此可知,在误差提取过程中,提取出的误差相关量Γm的方向会随着输入频率的变化而变化,进而导致提取出的时间误差值会随着信号频率变化而发生变化,最小变化周期为2fsub,即(1/2)fs,提取过程中输入信号频率与误差符号的关系见表2所列。

表2 提取过程中输入信号频率与误差符号的关系
综上所述,最终提取出的时间误差符号与真实时间误差之间的关系会随着输入频率在正、负之间进行周期性变化,并且最小周期为(1/2)fs。由此可得总的符号变化规律,见表3所列。

表3 系统输入信号频率与误差符号的关系
针对时间误差方向随输入信号频率变化的问题,本文提出了一种误差符号的判别模块,具体原理如下。对于(1)式,第1通道和第3通道相乘所得结果为:
(7)
对(7)式求期望,当采样点数N足够大时,(7)式中第2项的值为0,则有:
(8)
由于Δt2≪1,将ωin=2πfin/fs代入(8)式可得:
R0,2=E[y0[k]y2[k]]=
(9)
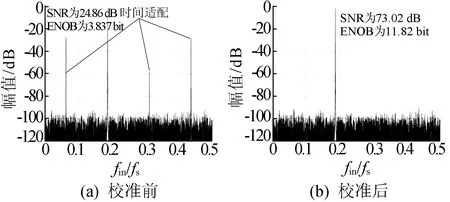
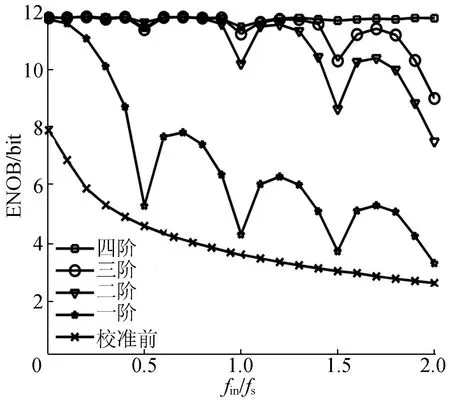
在第一奈奎斯特范围内,当0 图4 带符号判断的误差提取原理图 基于泰勒级数展开的时间失配误差补偿方案,是通过对第m通道子ADC的输出进行泰勒展开,消除误差多项式即可得到理想的采样输出[12]。对于第m个子通道,具有时间失配误差的输出泰勒级数展开式为: (10) 从(10)式可以看出,更高阶项的补偿意味着更高的精度,但也意味着更高的硬件复杂度和功耗,本节以三阶补偿为例,(10)式可以表示为: ym≈xm(t)+Δtmxm′(t)+ (11) 其中,xm′(t)、xm″(t)、xm‴(t)分别为理想采样信号的一阶、二阶、三阶导数。由于第m通道的理想输出xm(t)未知,因此使用ym代替xm(t),补偿后的输出可以表示为: (12) ym′、ym″、ym‴可由(11)式计算得到,代入(12)式可得: (13) (13)式中仅消除了误差的一阶项,文献[13]中提出了一种消除二阶和三阶误差项的有效方法,其中引入了级联结构以逐步补偿输出,其补偿结构如图5所示。 图5 高阶级联补偿结构 补偿后的输出可以表示为: (14) 从(14)式可以看出,经过补偿,只剩下四阶的误差项。在这种补偿结构中,由于出现误差估计值的高次方项,极大增加了算法的复杂度。为此本文采用一种改进的泰勒补偿算法,具体原理如下。 (15) (16) 根据(16)式搭建的时间失配误差校准原理图,如图6所示。图6中,z-1为延时哭。 图6 时序误差补偿原理图 改进后的泰勒补偿算法与文献[12-13]中泰勒补偿算法硬件消耗对比见表4所列。 从表4可以看出,改进的泰勒补偿算法有效地减少了硬件消耗。 表4 泰勒展开三阶硬件消耗对比 单位:个 当输入信号频率过大时,由于信号的欠采样和混叠带来的影响,需要相应地增加补偿公式中泰勒展开式的级数。 本文利用Matlab搭建了一个四通道12 bit TIADC的时间失配误差校准模型来验证本方法的正确性和有效性。假设输入归一化频率fin/fs为0.447、0.794、1.321,分别在不同阶数泰勒展开下进行校准,各通道采样时序误差Δtm=(0,0.01,0.03,0.02)Ts,Ts为采样时间。校准前后的FFT分析频谱如图7~图9所示。从图7~图9可以看出,校准后TIADC的有效位数(effective number of bits,ENOB)提升到11.82 bit以上,SNR提高了43 dB以上。 图7 fin/fs=0.046,二阶泰勒展开校准前、后频谱图 图8 fin/fs=0.813,三阶泰勒展开校准前、后频谱图 图9 fin/fs=1.321,四阶泰勒展开校准前、后频谱图 本文算法在泰勒展开前4阶的校准结果比较如图10所示,从图10可以看出,随着泰勒展开级数的增加,算法所能校准的输入带宽范围也增长,在泰勒展开四阶时已经能够较好地实现在第四奈奎斯特频域的校准。 图10 泰勒展开前4阶校准比较 本文提出了一种适用于宽带宽输入的TIADC时间失配误差校准算法。该算法利用闭环自适应的全数字校准方法对采样时序误差进行校准,在误差估计模块加入误差符号判别,误差补偿模块采用一种改进的泰勒补偿算法。与其他已有算法相比,本文算法结构简单,硬件消耗较少,没有输入带宽的限制,能够实现任意奈奎斯特频带下的校准,且仿真结果良好。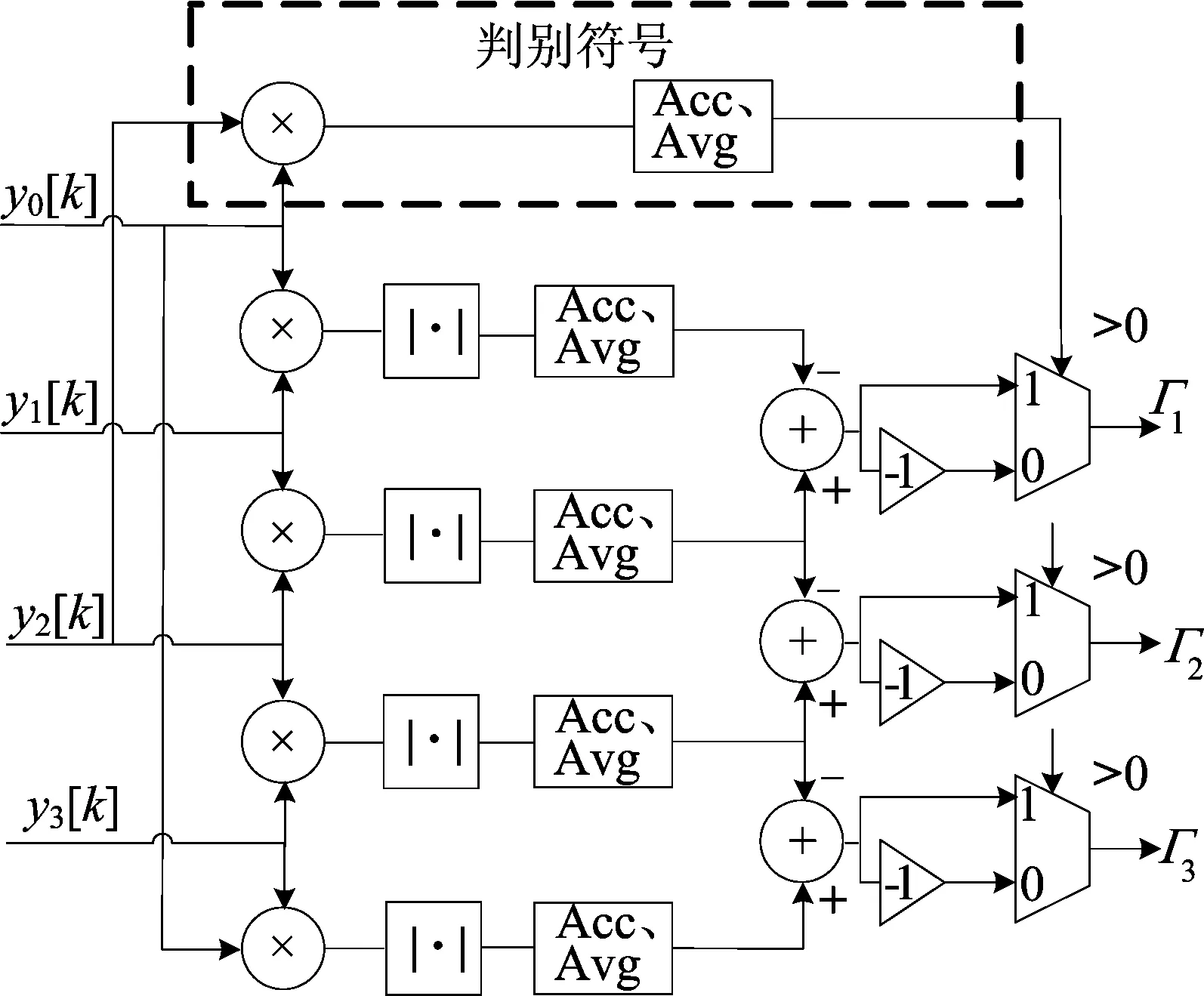
1.3 误差补偿
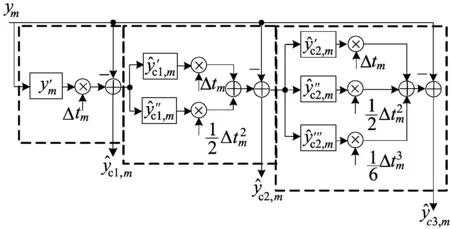
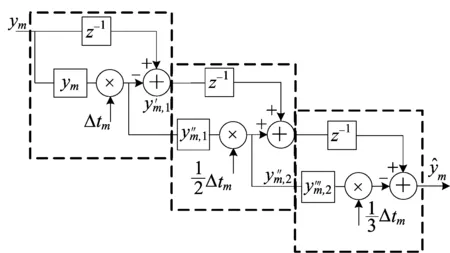

2 仿真结果


3 结 论
