新型隔振器的性能分析

周子博, 申永军,2, 杨绍普,2

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043)

0 引言

随着振动与噪声污染问题日益严重，对隔振器的要求也越来越高。双层隔振及浮筏隔振具有较好的隔振性能，在舰船动力机械设备中得到了实际应用。但是较大的中间隔振质量会带来较多弊端，如增大装置的结构尺寸和质量，增加振动控制的成本[1]，因此提高单层隔振性能具有实际意义。目前应用最广泛的隔振评定参数主要有力传递率、插入损失、振级落差和功率流传递率[2]。严济宽等[3]发现以往的隔振理论中都建立在刚性基础假设上，并没有考虑基座阻抗特性的影响，为此重新推导了柔性基础的插入损失与振级落差设计公式。后来学者们[4-5]对柔性基础下的经典评定参数进行了补充。王家林等[6]针对振级落差和插入损失的对应关系进行了研究，并指出了两指标的适用范围。Goyder et al[7]最早提出功率流概念，经过对简单无限均质梁的分析，认为传递到基座的功率流可以作为一种改进的性能指标。类似于传统的性能指标，研究者们[8-13]相继提出功率流的有效比、功率流传递率作为隔振系统的评价指标，其中，Pan et al[8]和Gadronio et al[9]提出功率流的有效比改进了隔振指标的准确性。霍睿等[13]对功率流传递率在隔振设计中的有效性进行了论证。

杠杆作为力放大机构已经用于隔振领域，并表现出良好的隔振性能。Flannelly[28]提出了动力反共振隔振器(dynamic anti-resonant vibration isolation, DAVI)，研究发现杠杆元件可以放大质量产生的惯性来抵消弹簧力，扩大隔振器的低频适用范围。文献[29]～文献[31]研究在大跨度桥、建筑等领域引入杠杆元件后，可以有效减小地震、风致振动等危害。文献[32]提出一种杠杆式非线性能量阱，在振动抑制方面比传统吸振器具有显著的优势，并研究了支点位置对系统稳定性的影响。

鉴于惯容与杠杆元件在振动控制领域中的良好性能，在基于柔性基础的单层隔振系统中引入两放大机构，得到了一种新型隔振器。经研究表明，两放大机构的加入，可以有效降低传递能量，证明了本文模型具有较好的隔振性能。

1 隔振模型

含有两放大机构的隔振模型如图1所示。m1表示主系统(被隔振设备质量)，k1表示隔振器的刚度，m2表示柔性基座的质量，并将弹簧k2、杠杆元件、惯容三元件串联于主系统与柔性基座，c′、k′表示基座的阻尼及刚度。x1、x2、x3分别表示主系统位移、杠杆元件与惯容分割点的位移、柔性基座的位移。同时忽略运动中的摩擦损失，惯容系数理想化为b，讨论模型在受到简谐激励F0cos(ωt)下的垂向隔振性能。

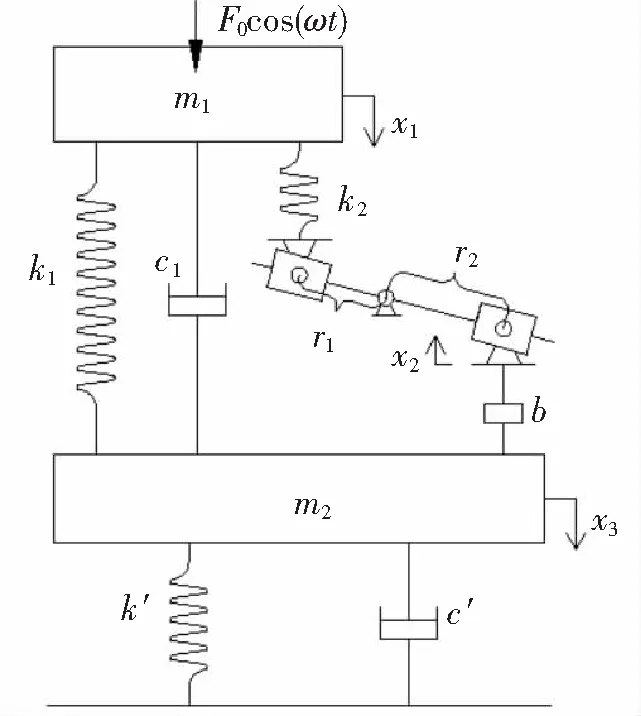
图1 隔振模型

根据牛顿第二定律，得到该振动系统的动力学方程

(1)

可以得到矩阵形式

(2)

式中，M为质量矩阵；C为阻尼矩阵；K为刚度矩阵，整理为

(3)

通过拉氏变换，将解和激励设为

(4)

将式(4)代入式(3)中，可以整理为矩阵ZX=F，Z代表阻抗矩阵

(5)

对式(5)求解，可得

(6)

式中

(7)

2 隔振指标

分析隔振器的隔振性能，经典的分析方法中利用力传递率、插入损失、振级落差等来评判传递到基座的力或振幅。但是传统的性能指标仅是涉及速度或力而不涉及两者之间的相位差，当减振目标是降低结构的声振幅或振动能量时，尤其在船舶领域，这些指标不再准确地反映隔振性能[7]。功率流作为评价隔振性能的重要参数，同时考虑力和速度的量值，使系统振动输出有了绝对度量。因此本文不仅考虑隔振系统的力传递率、振级落差等经典隔振指标，还考虑功率流传递率的情况。

2.1 力传递率

力传递是加入隔振器后传递到基座的动态力有效值与输入的动态激振力有效值的比值

(8)

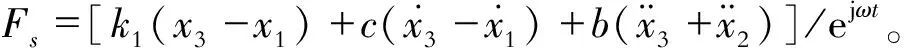
力传递率表示为极差(dB)形式

(9)

2.2 插入损失

插入损失表示加入隔振器后基座的响应有效值与加入隔振器前基座的响应有效值的比值

(10)

式中，x′为无隔振器时，柔性基础在相同力激励下的响应

(11)

式中，Q44=-ω2(m1+m2)+iωc′+k′。

将式(11)代入式(10)中，由于位移插入损失、速度插入损失、加速度插入损失相同(上下求导抵消)，可以得到插入损失率

(12)

2.3 振级落差

振级落差作为经典隔振指标，在我国国家标准和军标中有明确规定。参考舰船上各类隔振装置的隔振效果评价指标[13]，振级落差指被隔振系统的响应有效值与隔振后的基座振动响应有效值的比值

(13)

观察式(6)和式(13)可知，位移振级落差、速度振级落差、加速度振级落差相等。可以得到

(14)

2.4 功率流

在本文隔振系统中，力和速度都是简谐变化的，在一段时间内的平均功率更能反映传入系统的能量强度。功率流可表示为频率ω的函数，另外T=2π/ω，可以得到

(15)

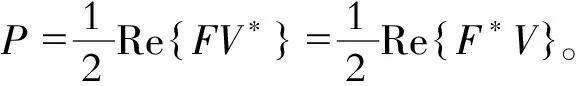
(16)

(17)

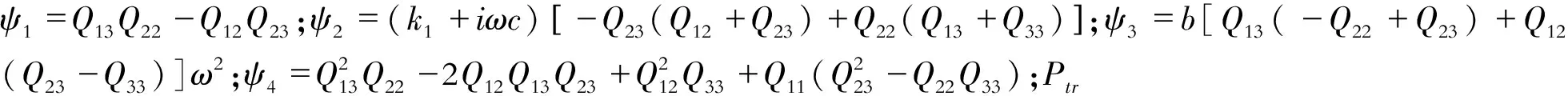
至此，已经推导出所有隔振指标设计公式。下文主要分析此模型的力传递率、振级落差、功率流传递率。

3 固有频率及反共振频率分析

当外界激励频率等于系统固有频率时会发生共振，故需要避免激振频率与固有频率相等的情况。而反共振指系统在某些特定频率的简谐激励作用下，系统某些部位出现简谐响应为零的情况，即在一定频率下系统某些部位的动柔度为零[33]，因此控制激振频率在反共振频率附近可以有效抑制振动。根据图1隔振模型，忽略阻尼的作用，可以得出

(18)

将式(4)代入式(18)，得到系统特征矩阵

(19)

令特征矩阵的行列式为零

|M-ω2K|=0

(20)

可以得到

Aω6-Bω4+Cω2-k1k2k3=0

(21)

利用盛金公式得出系统的3个固有频率

(22)

式中

(23)

令特征矩阵的行列式不为零，则复频响应函数为

(24)

记Δ=det|D|，整理为

(25)

式中，H11(ω)、H12(ω)、H13(ω)分别为各阶振幅与力的比值。式(25)分子等于零代表各阶产生反共振现象，主要考虑传递到基座的力及能量的变化，故令H13(ω)=0，整理得到基座的反共振频率

(26)

(27)

4 性能分析

本文采用某隔振试验系统，应用文献[34]中的参数。参数如表1所示。

表1 参数值

图2与图3给出了不同惯容值与放大比对隔振系统力传递率的影响。可以清楚地看出，随着惯容值以及杠杆放大比的增大，隔振系统的第一、二阶固有频率向坐标轴左移，数值减小。同样可以得出，系统反共振频率位于力传递率的峰谷位置，意味着系统隔振效率最好。值得一提的是，由于惯容和杠杆元件的放大作用，促使反共振频率向低频移动，提高了隔振系统在低频的隔振效率。

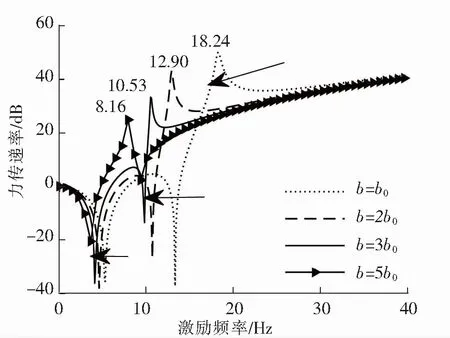
图2 不同惯容值下力传递率与频率的关系

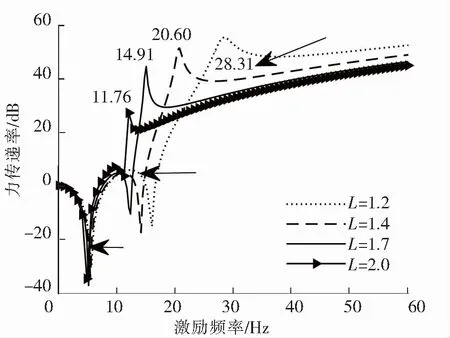
图3 不同放大比下力传递率与频率的关系

另外，隔振系统的振级落差由图4和图5给出，传递功率流率如图6和图7所示。同时为了更直观地了解惯容值和放大比对固有频率和反共振频率的影响，图8和图9分别给出了固有频率和反共振频率与惯容值和放大比的关系。

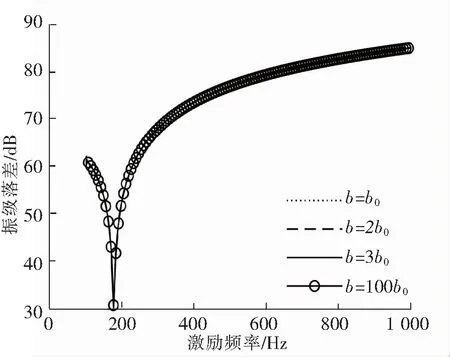
图4 不同惯容值下振级落差与频率的关系

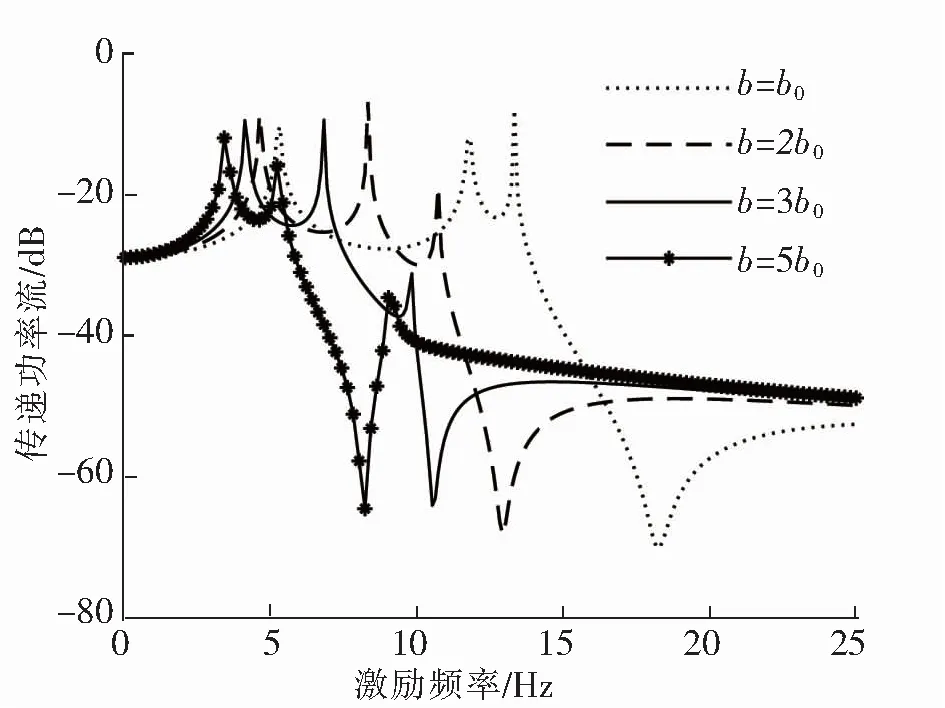
图6 不同惯容值下传递功率流与频率的关系

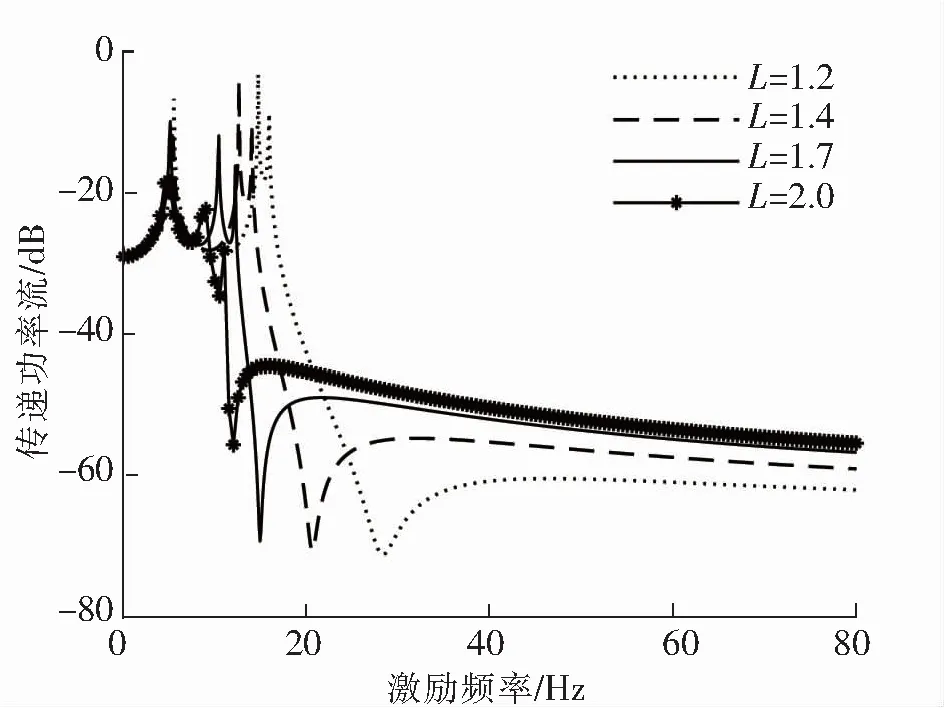
图7 不同放大比下传递功率流与频率的关系

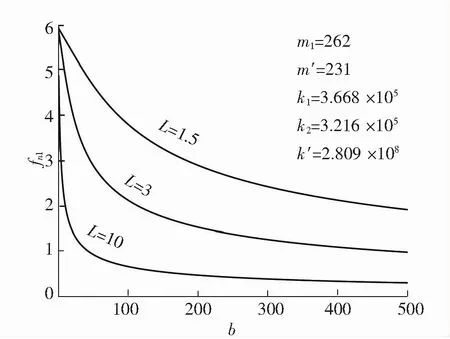
图8 不同放大比下第一阶固有频率与惯容值的关系

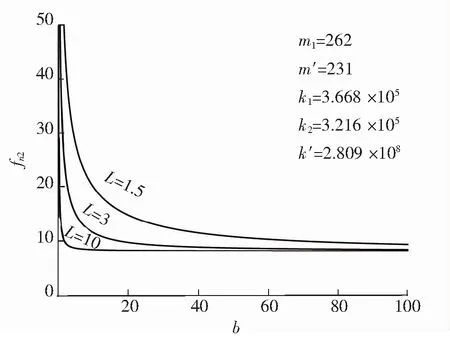
图9 不同放大比下第二阶固有频率与惯容值的关系

振级落差在低频区域与力传递率表现类似，故截取高频区展开分析。如图4所示，第三阶固有频率不变，因此惯容值的变化并不会影响高频下隔振系统的振级落差，但随着频率的增加隔振性能越好。由图5可知，在激振频率为1 000 Hz时振级落差会趋于相等，激振频率等于第三阶固有频率时，系统发生共振，振级落差达到最低点，隔振性能最差。并且在高频区随着放大比的增大，隔振性能有所下降。

图6和图7给出了隔振系统的低频传递功率流特性。从图6和图7可知，随着频率的增加，隔振系统的传递功率流总体减小，隔振效率越好；随着惯容值和放大比的增大，会出现共振频率及间距减小的现象，有利于摆脱共振频带。另外在反共振频率附近，隔振效率最高。需要指出的是，在二阶固有频率附近有2个较小的波峰，说明传递功率流综合考虑了力和速度的幅值和相位的关系。

图8～图11清晰地显示了隔振系统的三阶固有频率以及反共振频率与控制变量(惯容值与放大比)的关系。可以看出第一、二阶固有频率及反共振频率随惯容值的增大而减小，相同惯容值的情况下，放大比越大固有频率及反共振频率亦随之减小。从图10可以直观地看出，第三阶固有频率值独立于惯容值与放大比的变化，保持在175.7 Hz。当惯容值及放大比趋于无穷时，第一阶固有频率与反共振频率趋于0，第二阶固有频率趋于8 Hz。

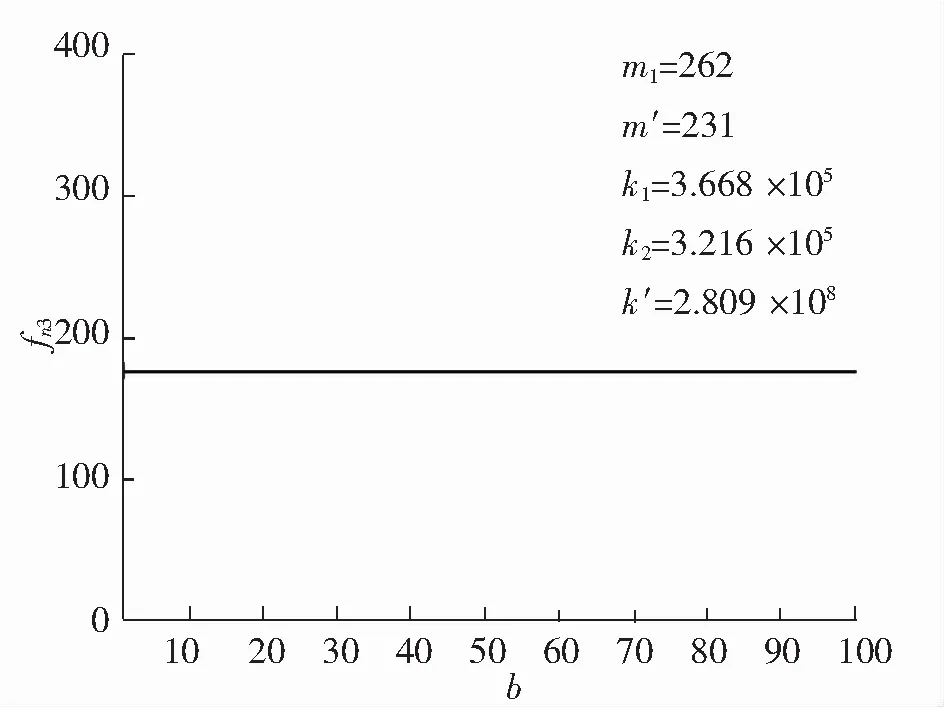
图10 不同放大比下第三阶固有频率与惯容值的关系

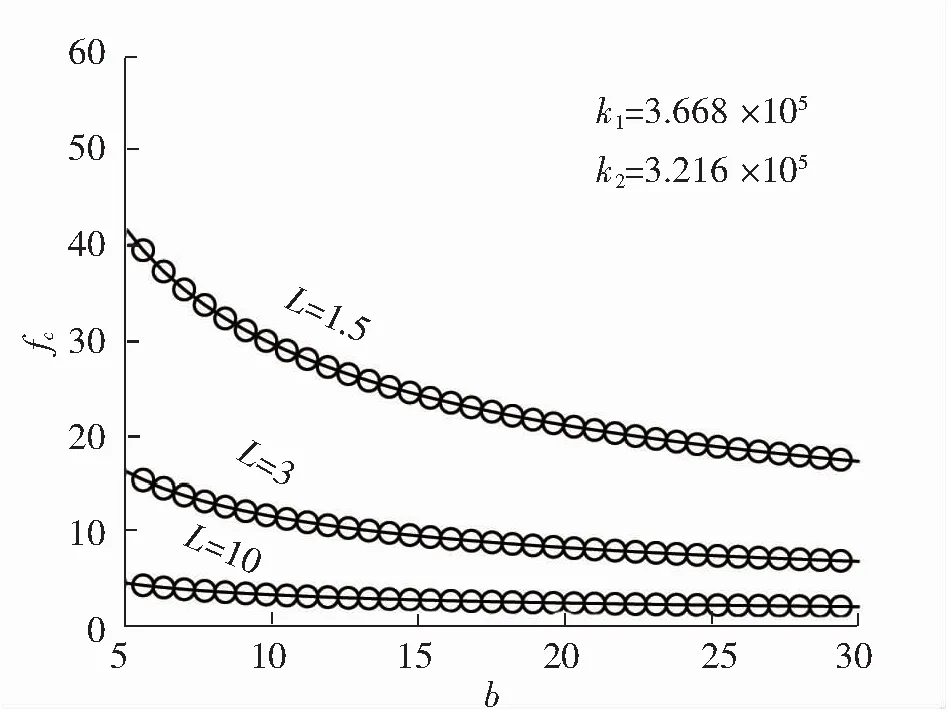
图11 不同放大比下反共振频率与惯容值的关系

5 模型对比

为了证明含两放大机构的新型单层隔振系统的优势，将本文模型与参数相同的普通单层隔振模型、含惯容的单层隔振模型进行了比较。据表1中的参数，另取放大比L=3L0和惯容值b=b0，模型对比见图12。

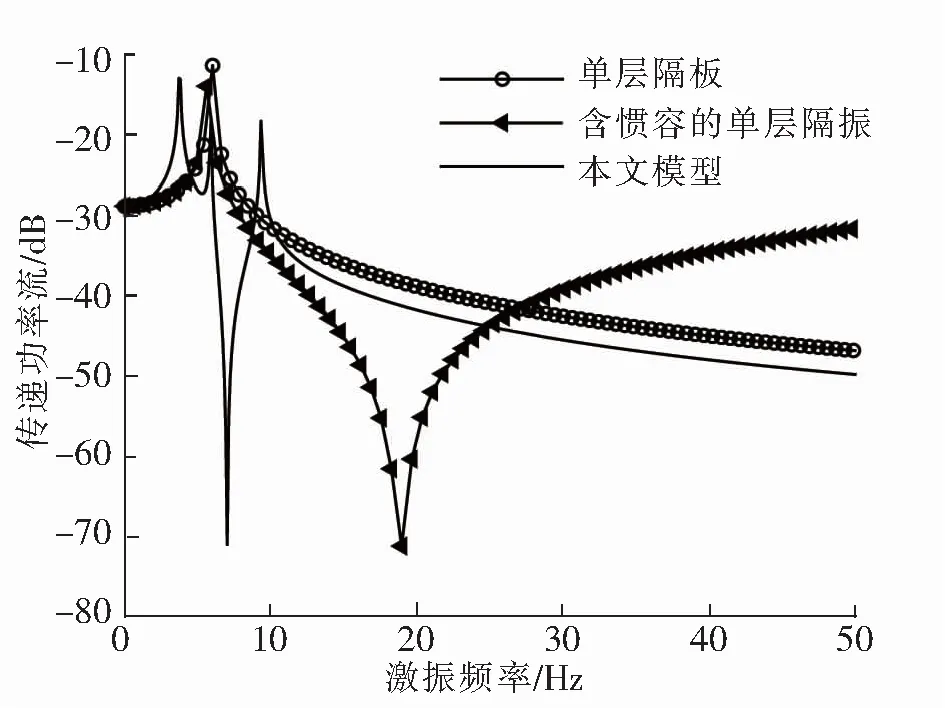
图12 模型对比

从图12可以看出，含有惯容的单层隔振系统存在反共振频率，在20 Hz附近要比单层隔振系统性能更优，但在高于30 Hz后会失去优势；本文隔振系统却避免了单层隔振系统与含惯容的单层隔振系统的缺陷，在高频与低频都有较好的表现。另外可以通过改变放大比或者惯容值来改变共振频率，适应不同隔振需求，因此从能量角度也验证了含有惯容与杠杆元件的隔振系统的优势。

6 结论

研究了一种含有惯容和杠杆元件的柔性基础单层三自由度隔振模型，通过解析计算得到模型传递到基座的力传递率、振级落差、插入损失以及功率流的设计公式。通过对参数的研究，发现两放大机构可以不同程度缩小共振频率，减小共振区频带。通过与单层隔振系统以及含惯容的单层隔振系统的比较得出，本文模型在低频与高频区都改善了隔振性能，还可以通过改变两放大元件参数适应不同工程需求。