足球运动中不同旋转球的运动轨迹及力学分析

牛曼兰

(安徽新华学院 通识教育部, 合肥 230088)

足球运动中的旋转球指的是足球运动员运用不同的脚法，踢出球并使球在空中向前作弧线运行的过程[1]。根据脚法的不同，可以将足球旋转分为内旋球与外旋球。对不同旋转球进行力学分析，能够为日常的足球训练提供科学的训练数据，帮助足球运动员提高自身技术[2]。分析不同旋转球的运动轨迹，能够科学规划足球运动过程中旋转球的方向，帮助足球运动员取得好成绩，为此研究足球运动过程中不同旋转球的运动轨迹及力学分析是很有必要的。

国外研究旋转球的运动轨迹及力学分析起步较早，已经形成成熟的分析研究体系，并已成熟地运用于足球运动员的日常训练中[3]。国内针对该方面的研究起步较晚，各个专业研究机构对于足球运动中旋转球的研究成果及文献资料较少，仍需不断改进学习。提出足球运动中不同旋转球的运动轨迹并对其进行力学分析，建立旋转球坐标系分析旋转球运动过程，对不同旋转球进行轨迹追踪，通过非线性变换得到轨迹状态向量，确定运动轨迹起始点，采集运动过程的轨迹状态向量，得到旋转球的运动轨迹。

1 足球运动中不同旋转球的运动轨迹及力学分析

1.1 旋转球受力分析

对旋转球进行受力分析时，首先定义足球的旋转轴，以足球停滞在实际轨迹中的某个状态为研究目标，结合空气在足球旋转过程中的流速[4]，建立坐标系如图1所示。以旋转状态的足球旋转轴为坐标系的Z轴，得到力坐标系：

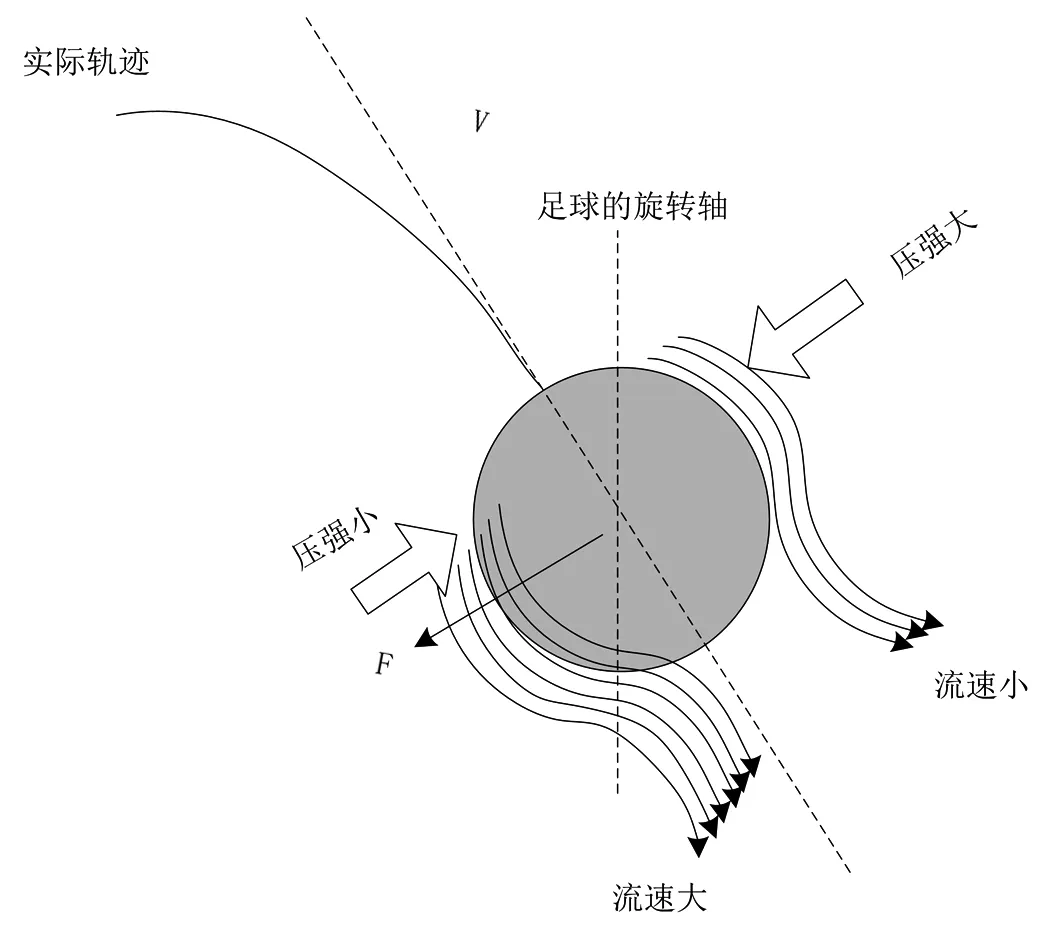
图1 建立的旋转球坐标系

由旋转球坐标系可知，将旋转球的流速方向作为x轴，旋转球受到压强的方向为y轴。根据坐标系的方向分析可得到足球旋转球在空气中主要受到重力Fg，空气阻力Fa以及马格努斯力Fm的作用。定义上图1旋转球的时刻t下，旋转球的运动速度为：

v(t)=[vx(t),vy(t),vz(t)]T，

(1)

式(1)中，T表示旋转球的飞行时间，vx(t),vy(t),vz(t)分别表示不同轴向的运动速度。进而计算得到旋转球的旋转角速度，计算公式为：

W=[ωx,ωy,ωz]T，

(2)

式(2)中，ωx,ωy,ωz分别表示旋转球不同轴向的角速度。综合上述角速度及旋转速度的数值，计算得到该时刻旋转球的重力、空气阻力以及马格努力的数值：

(3)

式(3)中，m为足球的重量，g表示重力加速度，Cd表示空气阻力系数，Cm表示马格努斯力系数，ρ表示标准气压下的空气密度，A表示足球的横截面积，r表示足球的半径，其余参数含义不变。由上述计算公式可知，空气阻力大小与旋转球的飞行速度平方成正比。当足球一侧运动速度和旋转速度方向不平行时，旋转球的一侧在空气的作用下，飞行速度与旋转速度叠加变大，旋转球的另外一侧速度与空气作用相抵消，此时旋转球两侧存在压力差，形成旋转球[5]。根据流体力学原理，该部分压力差为马格努斯力，综合上述计算公式(3)中的力，得到旋转球的运动过程，表达式为：

(4)

式(4)中，CD表示足球表面的粗糙程度，V(t)表示足球的加速度。根据计算出的数值，采用高速摄影机对足球旋转运动过程进行采样[6]，设置采样帧率为120 fps，在一个采样周期内，保持足球的加速度和速度不变，在一个旋转状态内，旋转球的离散运动就可表示为：

(5)

式(5)中，k表示迭代周期，kd与km分别表示旋转球的不同受力的迭代系数。其余参数含义保持不变。轨迹跟踪上述受力分析得到的旋转球的运动过程，最终完成对不同旋转球的运动轨迹及力学分析。

1.2 不同旋转球的轨迹追踪

在上述分析得到的旋转球运动表达式下，定义旋转球停止旋转过程表示迭代过程结束，计算迭代过程产生的噪声，计算公式为：

(6)

式(6)中，Cn表示升力系数，D表示足球的直径，其余参数含义不变。在上述噪声值的影响下，预测旋转球的状态向量，将上述计算得到的噪声值作为先验估计值，状态向量就可表示为；

(7)

式(7)中，X(k|k-1)表示旋转球状态变量的先验估计值，P(k|k-1)表示状态变量协方差的先验估计值，Ak表示运动过程函数F对状态变量的偏导，Qk表示噪声向量。根据上述状态向量数值，划分得到不同旋转球的状态数据数量，如表1所示。

表1 不同旋转状态的数据矢量

追踪表1三种旋转球的旋转属性时，利用非线性变换处理上述三种旋转属性的输出数据矢量，非线性变换过程如图2所示。

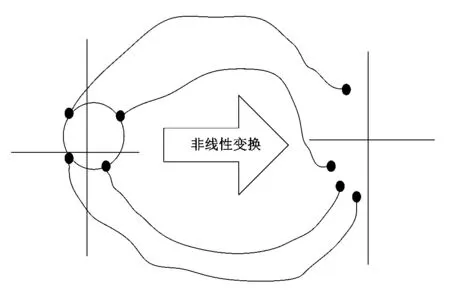
图2 非线性变化过程

由图2所示的非线性变化过程可知，设定输出数据矢量的采样点，计算非线性变换后输出数据采样点的方差及权重，根据方差值的分布距离，确定变换过程中的比例系数，完成对不同旋转球的状态追踪，追踪完毕后，形成旋转球的运动轨迹。

1.3 运动轨迹获取

根据上述非线性变换过的轨迹状态向量确定运动轨迹起始点，为了简化轨迹跟踪过程中的计算过程，将分布距离看作常数，不同旋转球的坐标采样点就可表示为：

(8)

式(8)中，κ(k)表示连续采样运动过程中第k类的层级参数。根据上述采集点的追踪结果，得到采样点旋转球的坐标，汇总采集点的坐标数值，如表2所示。

表2 轨迹采集点坐标

将表2所示的旋转球在三项坐标作为轨迹数据集，采用非线性滤波处理表2中坐标数值，对旋转球运动轨迹不断更新，更新表达式如下：

(9)

式(9)中，Kn表示轨迹更新过程，n表示旋转球的采集点，Qx，Qy，Qz分别表示三个轴向的数值，α表示旋转球实际运动轨迹与三个轴的夹角，Fn表示旋转球的合力数值。根据上述整合形成的采样点计算公式，在一个三维坐标下模拟得到旋转球的运动轨迹，如图3所示。

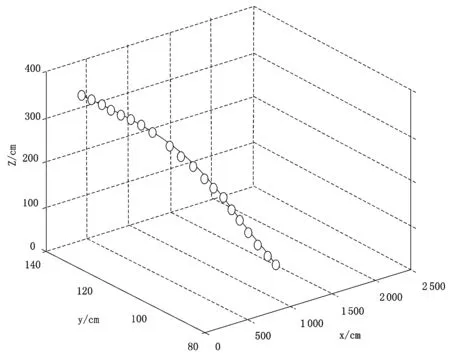
图3 旋转球飞行轨迹

由图3所示的旋转球飞行轨迹，最终在力学分析前提下，完成对足球运动中不同旋转球运动轨迹的研究。

2 仿真实验

2.1 实验准备

采用一个塑料颗粒模拟足球运动中的旋转球，控制该塑料颗粒直径为0.4 cm，密度为1 g/cm3，质量为0.1 g。选用高速摄像机、秒表、水平尺作为实验仪器。采用的高速摄像机和镜头的硬件参数如表3所示。

表3 实验仪器硬件参数

采用如表3所示的各项参数控制下的实验器材，选用三个形状不同的内筒作为塑料球的运动轨道，模拟不同旋转球的轨迹情况。设定固体颗粒在内筒内的速度，如表4所示。

表4 设定的固体颗粒速度值

在表4所设定的速度值下进行实验，不同的转速与角速度对应着不同旋转球的状态，分析小球在设定的内筒内的轨迹及受力情况。

2.2 实验结果及分析

基于上述实验准备，采用高速摄像机得到颗粒小球在不同转速下的运动轨迹，如图4所示。

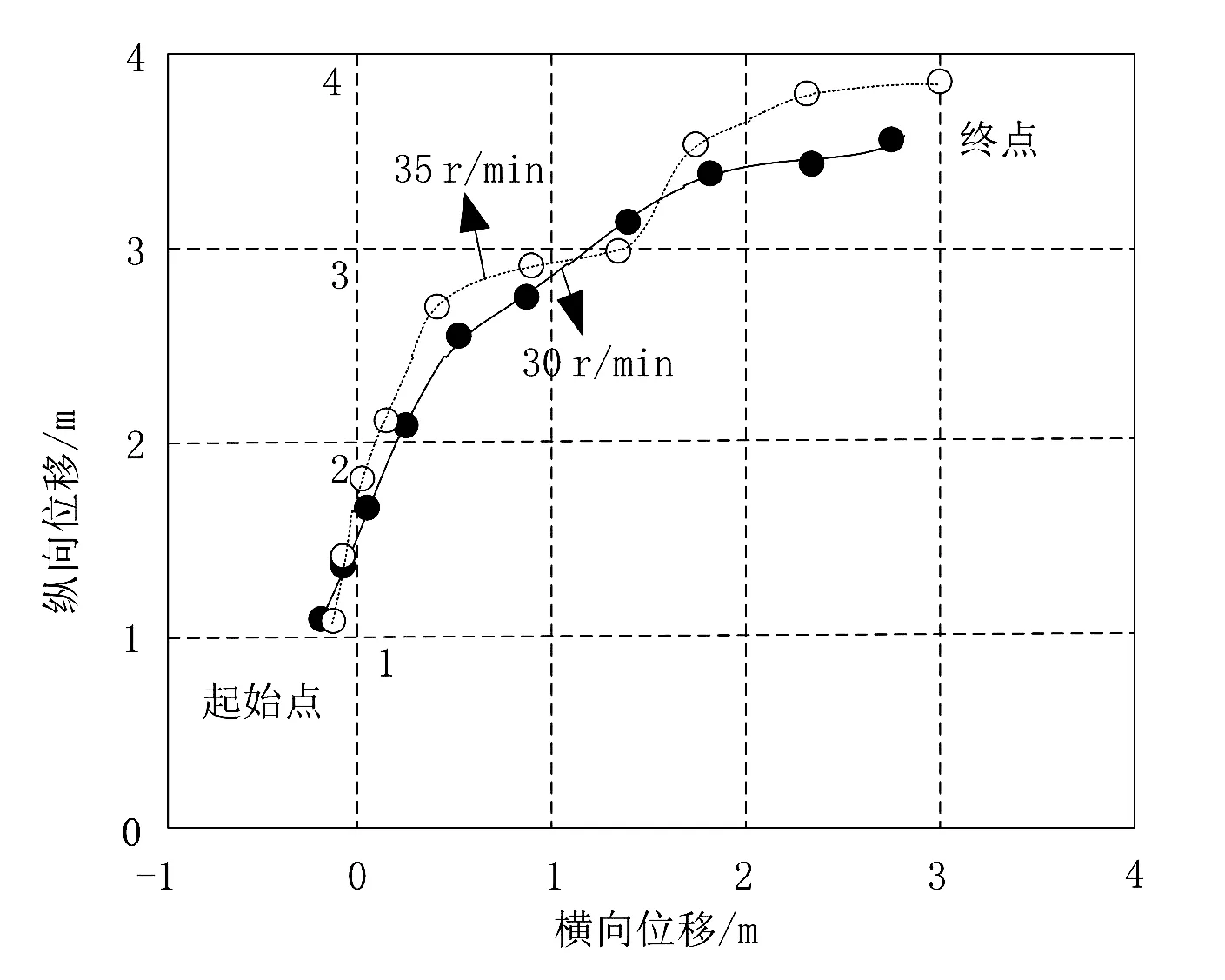
图4 不同转速下小球的运行轨迹

由图4所示的运行轨迹可知，在30 r/min转速下，小球受到的离心力与差异性旋转惯性力的作用方向相反，旋转惯性力的数值大于其离心力的数值，小球做向心运动。在35 r/min转速下，小球主要受到离心力与差异旋转惯性力的作用，且该两种力的方向相同，小球做离心运动。

保持上述实验环境不变，以转速为30 r/min的小球作为实验对象。在实验准备的内筒中灌入水，控制水流的速度为匀速，来模拟足球在旋转运动过程中受到的空气压力，采用文中研究的力学分析方法进行实验。以水平尺显示的刻度作为划分对象，平均地将内筒长度划分为七个刻度，标定内筒七个测点，七个测点小球的基本参数如表5所示。

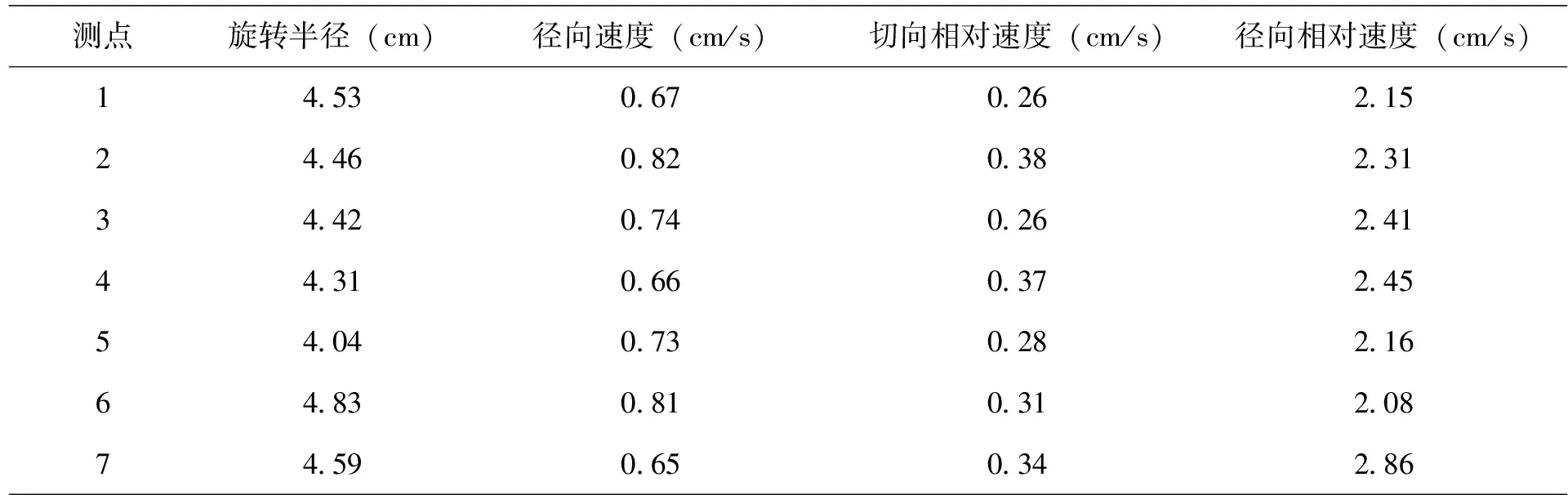
表5 小球经过测点速度基本参数

在表5所示的参数控制下，考虑到小球在内管中径向受力数值的不同，分析得到该转速的小球的受力情况如图5所示。

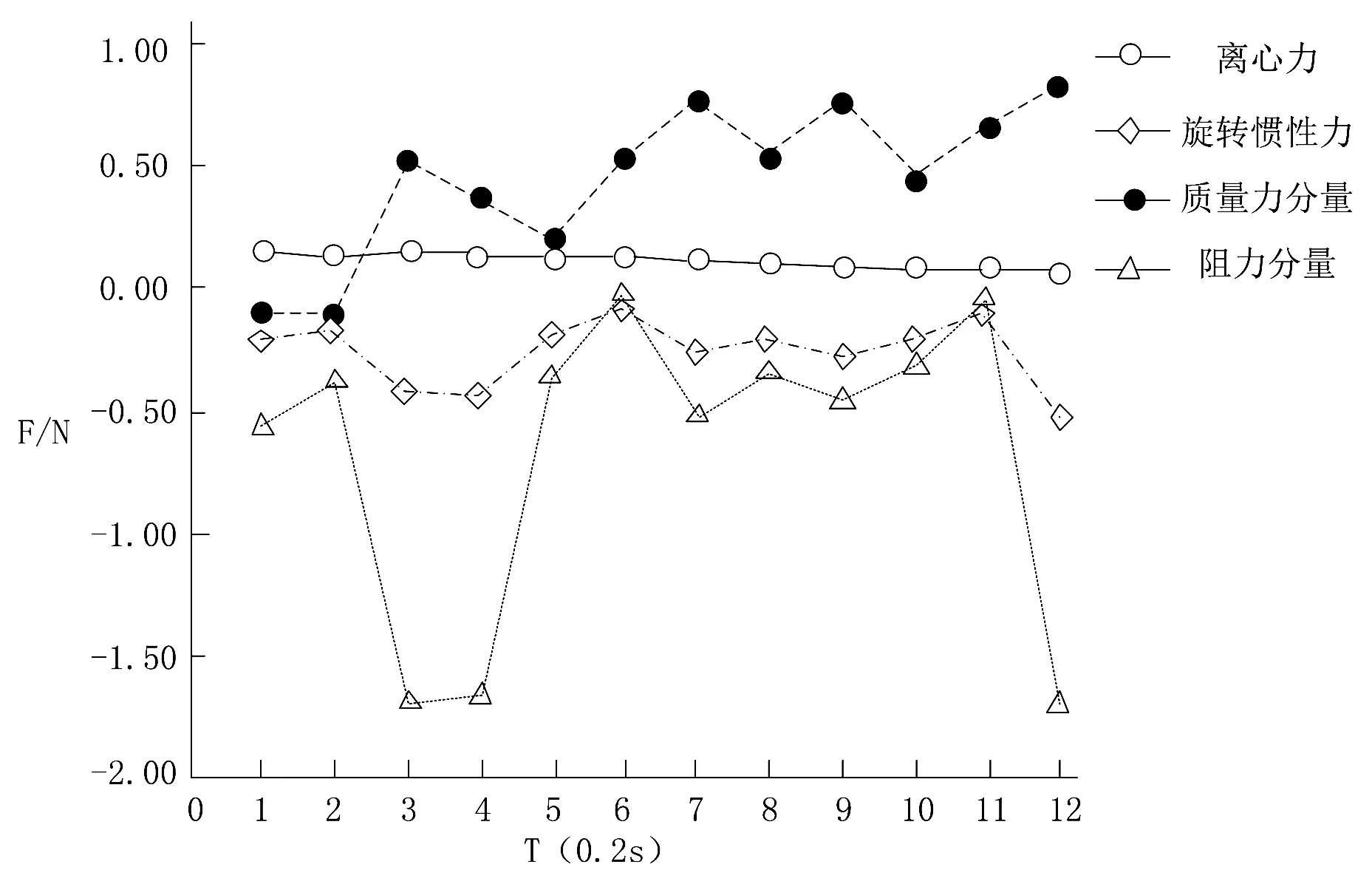
图5 小球的受力情况

由图5所示的小球受力情况可知，在模拟过程中小球共受到4个作用力的影响，由不同作用力的数值可知，小球在内筒中受到几乎为零数值的离心力。随着时间不断增加，质量力分量不断增大且为正方向，质量力分量随着时间不断增加，平均值保持在-0.2 N左右。而阻力分量表现不稳定，在0.6 s到0.8 s之间与2.4 s时受到力的负方向1.7 N的力，表明在模拟的旋转球环境中，在不同的轨迹点中，存在着多种阻力分量。

综合上述实验准备及分析，完成对文中设计的运动轨迹及力学分析方法的验证。实验结果表明，在30 r/min转速下，模拟旋转球做向心运动，在35 r/min转速下，小球做离心运动。小球受离心力、旋转惯性力、质量力分量及阻力分量4个力的共同作用，形成旋转球。

3 结语

足球运动一直是体育运动研究领域的重点，基于旋转球的运动轨迹较为复杂，国内对其运动及受力研究较少，因此，提出不同旋转球的运动轨迹及力学分析，并采用塑料颗粒模拟足球运动中的旋转球，通过实际操作验证了研究方法的有效性。

研究足球运动中不同旋转球的运动轨迹及力学分析，能够更加科学地掌握足球的旋转过程及运动轨迹，为我国足球运动提供更加科学的训练方案，帮助我国足球运动不断发展。