基于柔性衬底的双端固支梁RF MEMS开关相位特性研究*

隋东辰，陈立军，韩 磊*

(1.东南大学电子科学与工程学院，江苏 南京 211189；2.东南大学MEMS教育部重点实验室，江苏 南京 210096)

相比于传统的刚性器件，柔性器件由于自身特殊的可弯曲性，在复杂的非平面条件下具有不可替代的优势。同时由于高效的制造工艺、较低的成本，柔性器件逐渐被应用于通信、显示、医疗、传感等领域[1-3]，具体包括柔性传感器/执行器、可穿戴医疗设备等。RF MEMS柔性器件具有可弯曲、体积小、重量轻和成本低的优点，在雷达/物联网领域具有广泛的应用前景。RF MEMS开关是构成射频系统的最基本器件，其凭借着自身的超高微波性能和近零功耗的优势正在逐步取代传统射频开关，成为了国内外近年的研究热点[4]。针对双端固支梁RF MEMS开关，在结构方面，文献[5]提出了一种在LCP基底上的双端固支梁结构，在40GHz频率下相比于使用硅基底有更低的功率损耗。针对模型建立方面，文献[6]建立了一种RF MEMS双端固支梁结构并对其动态特性进行了研究。文献[7]针对双端固支梁结构RF MEMS开关进行建模，并从力学性能和微波性能方面对模型进行了实际测试验证。然而，目前对双端固支梁RF MEMS开关的研究大多数在吸合电压与吸合时间[8-10]、微波性能[11-13]及工艺[14-15]方面，针对双端固支梁RF MEMS开关弯曲条件下对微波信号相位影响的研究尚属于空白。但是，由于柔性衬底弯曲导致射频信号相位偏移会显著影响功率合成效率、移相精度等射频电路关键指标，因此研究不同弯曲曲率下RF MEMS开关相位的变化是非常有必要的。

本文提出了一种柔性双端固支梁RF MEMS开关相位特性模型，通过模型计算和软件仿真分析了不同衬底弯曲曲率条件下双端固支梁RF MEMS开关的相位偏移量，并基于LCP柔性衬底对开关进行了制备表征。实测结果显示，当柔性衬底弯曲曲率从0增大到33 m-1时，RF MEMS开关的相位偏移量绝对值不断增大，中心频率10 GHz处相位偏移由0°变化到-2.72°，8~12GHz频率范围内实测值和仿真值误差小于9.5%，实测值和模型计算值误差小于10.9%，测试结果与模型及仿真结果吻合较好，验证了模型的正确性和有效性，为后续柔性双端固支梁RF MEMS开关电路的相位特性分析设计提供了理论基础。

1 相位特性模型

本文采用的双端固支梁RF MEMS开关由双端固支梁、共面波导信号线、共面波导地线、驱动块以及锚区组成，如图1所示。当驱动块没有施加驱动电压时，双端固支梁位于共面波导信号线上方，微波信号从信号线通过，RF MEMS开关处于开态。当驱动块施加较大驱动电压时，驱动块和梁之间的静电力迫使梁向下运动，直至梁与共面波导信号线吸合，此时信号线处于接地状态，微波信号被全反射，RF MEMS开关处于关态[16]。

图1 双端固支梁RF MEMS开关结构示意图

本文针对双端固支梁RF MEMS开关开态时的相位特性进行研究。在理想情况下，双端固支梁膜桥可以看作一平直结构，如图2所示。当柔性衬底弯曲时，衬底与双端固支梁膜桥的距离减小。双端固支梁的长度为L，衬底曲率半径为R，可以得到弯曲半角(弧度制)为:

膜桥与衬底的实际距离为:

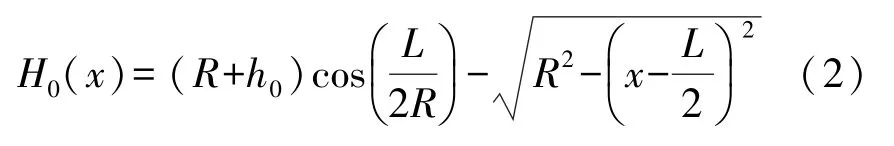
式中:h0为膜桥与衬底的初始间距，x为膜桥上该点到梁左端的水平距离。在实际情况中，由于加工工艺产生桥内应力的影响，膜桥形状不再是平直的梁，而是有一定的形状变化，如图2点实线所示。形状变化后的膜桥用正弦函数曲线进行近似，近似后膜桥与衬底的实际距离为:

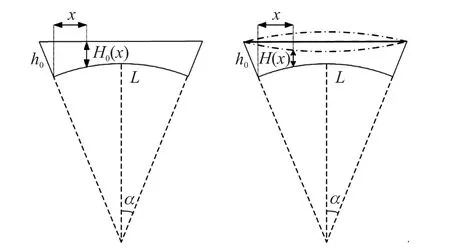
图2 理想模型与近似后模型

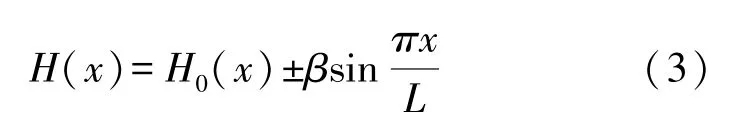
式中:β为膜桥弯曲的比例系数，可以表征制造出的梁弯曲程度的大小，上式中取“＋”为膜桥凸起，取“-”为膜桥凹陷。

典型的双端固支梁RF MEMS开关的等效电路如图3所示。

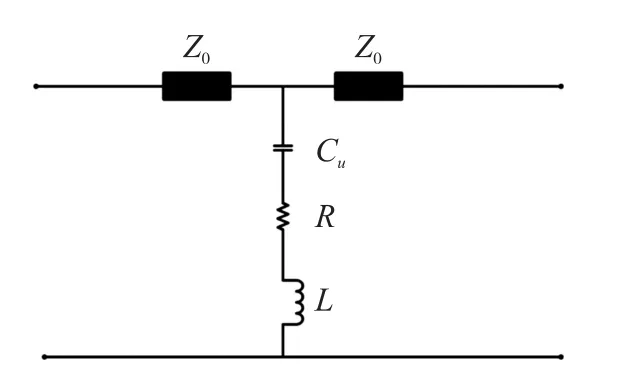
图3 双端固支梁RF MEMS开关开态等效电路模型

当双端固支梁RF MEMS开关处于开态时，根据等效电路可以计算得到[17]:

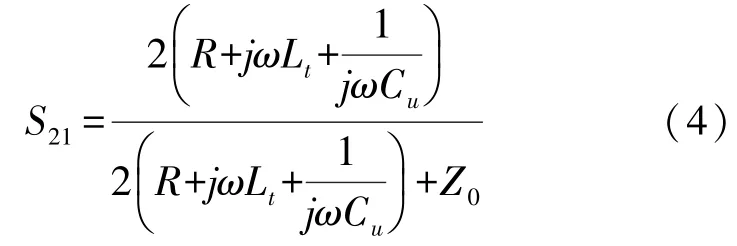
式中:Z0为CPW传输线的特征阻抗，Cu为双端固支梁RF MEMS开关开态时的等效电容，R为双端固支梁开关的等效电阻，Lt为双端固支梁开关等效电感，ω为通过微波的角频率。忽略电阻对传输性能的影响，化简得到:

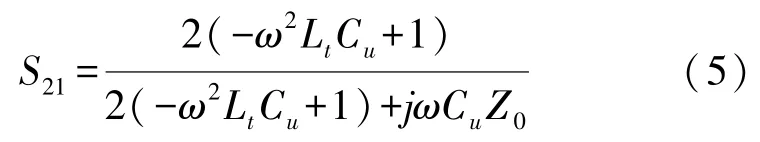
根据上式，可进一步求得相位为:

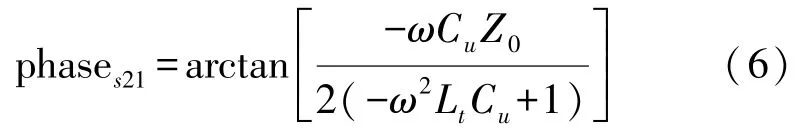
式中:总电感Lt等于弹簧等效电感Ls与平板等效电感Lf之和。弹簧等效电感可由以下公式计算:

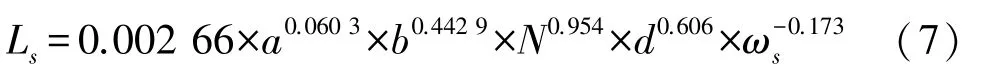
式中:N是交叉梁的数量，a和b是靠近锚区的交叉梁和枢轴梁的长度，d是交叉梁之间的距离，ωs是弹簧等效电感的宽度。平板等效电感可由以下公式计算:

式中:D和W分别是平板等效电感的长度和宽度。

当衬底弯曲时，信号线与桥梁之间距离变小。使用修正后的模型对电容进行计算。同时考虑边缘电容的影响，得到RF MEMS开关开态电容为:

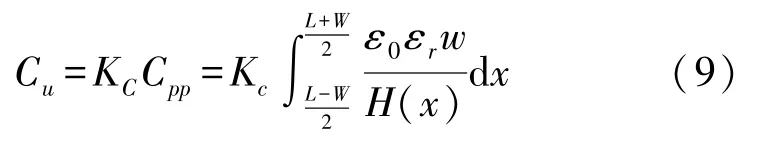
式中:Cpp为平行平板电容，w为梁宽，H(x)为式(3)中计算得到的高度，Kc是边缘电容比率，可由以下公式计算:

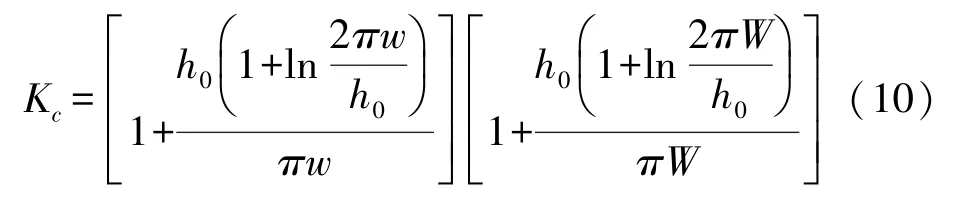
从上述公式可以看出，当曲率半径R减小时，衬底与梁的距离变小，导致了电容Cu的增大。计算出电容Cu与电感Lt后，代入式(6)，就可以计算出不同曲率下RF MEMS开关的相位值。

进一步，可以得到弯曲曲率为m时RF MEMS开关相位值相对于衬底未弯曲时(曲率为0)RF MEMS开关的相位偏移量:

相位偏移量的大小可以表征衬底弯曲对RF MEMS开关相位值的影响。

2 设计与仿真

2.1 HFSS仿真模型建立

本文采用Ansoft HFSS软件对双端固支梁RF MEMS开关进行相位特性的分析。为保证一致性，本文仿真以及理论计算均采用实际器件尺寸的测量值，各项参数如表1所示。

表1 双端固支梁RF MEMS开关模型尺寸

模型中膜桥为凹陷形状，且采用CPW传输线的G/S/G宽度为20μm/210μm/20μm，特征阻抗是50Ω，衬底曲率分别选取平直不弯曲、曲率半径为50 000μm、45 000μm、40 000μm、35 000μm，即曲率分别为0、20.0 m-1、22.2 m-1、25.0 m-1、28.6 m-1，HFSS模型如图4所示。

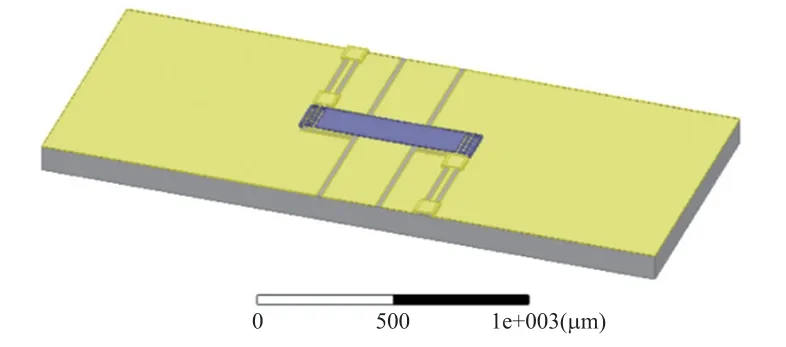
图4 双端固支梁RF MEMS开关的HFSS模型

在仿真时，工作频段为8 GHz~12 GHz，在双端固支梁RF MEMS开关的信号线两端施加激励，并变换不同的衬底弯曲曲率，得到不同情况下RF MEMS开关的相位值。

2.2 仿真结果

在HFSS模型建立的基础之上，得到了模型的仿真结果，并与理论模型计算值进行对比，如图5所示。以未弯曲时的开关相位为基准值(0°)，计算出不同弯曲曲率下双端固支梁RF MEMS开关相位的偏移量。图5(a)代表10 GHz下不同曲率开关相位偏移量的模型计算值与仿真值结果，图5(b)代表8 GHz~12 GHz不同频率下的开关相位偏移量的理论模型计算值与仿真值结果。

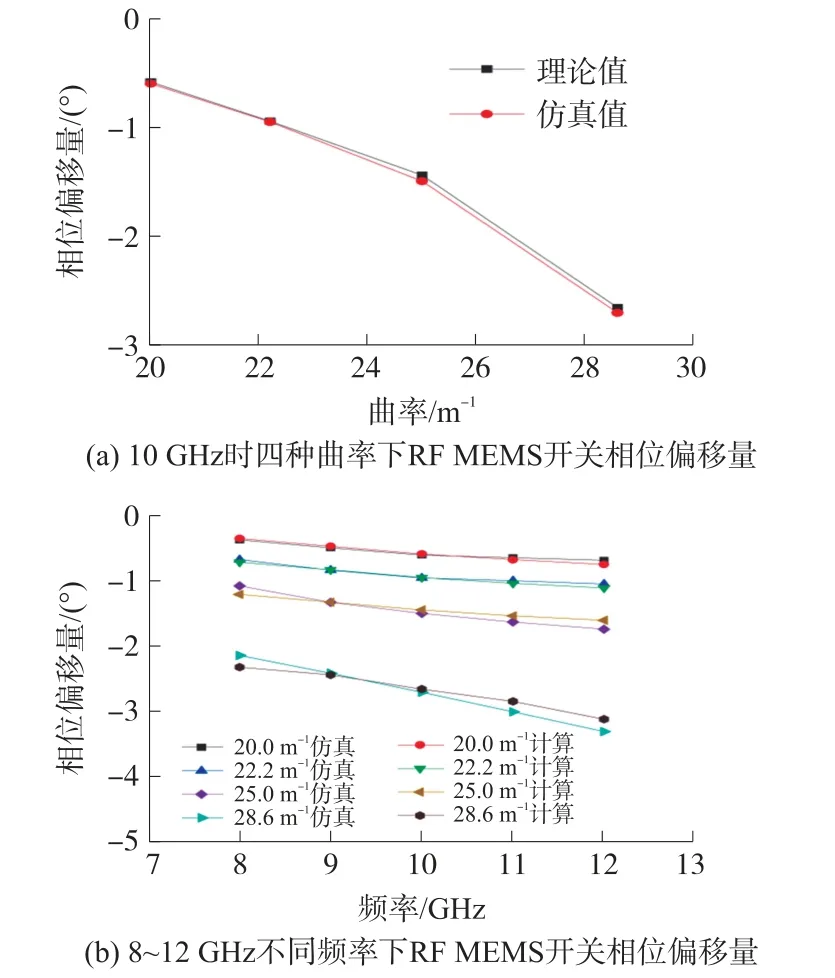
图5 衬底弯曲对开关相位偏移量影响的计算值与仿真值

由图5(a)可以看出，在10 GHz信号条件下，RF MEMS开关从平坦情况增加到曲率为28.6 m-1时，开关相位偏移量仿真值由0°变化到-2.70°，且随着曲率的逐渐增大，其相位偏移量绝对值相应增大。在10 GHz频率下，仿真值与模型计算值贴合较好，最大相对误差小于3.6%。由图5(b)可以看出，随着频率的增大，开关相位偏移量绝对值增大，仿真值与模型计算值变化规律相符，最大误差小于8.0%。

由理论模型计算和仿真分析结果可知，当衬底曲率变大时，其翘曲程度相应变大，导致信号线与梁的距离变小。由相位特性模型的电容公式可以推出双端固支梁和信号线之间的等效电容变大，导致相位偏移量绝对值增大。仿真结果与理论模型计算结果符合良好。

3 工艺制备

3.1 工艺步骤

本文采用的双端固支梁RF MEMS开关是以LCP柔性基板为衬底，利用微电子表面加工工艺制造出的器件。制造过程中采用了溅射、光刻、刻蚀和电镀等工艺，具体的工艺步骤为:

①LCP衬底准备，溅射一层金种子层，如图6(a)所示。

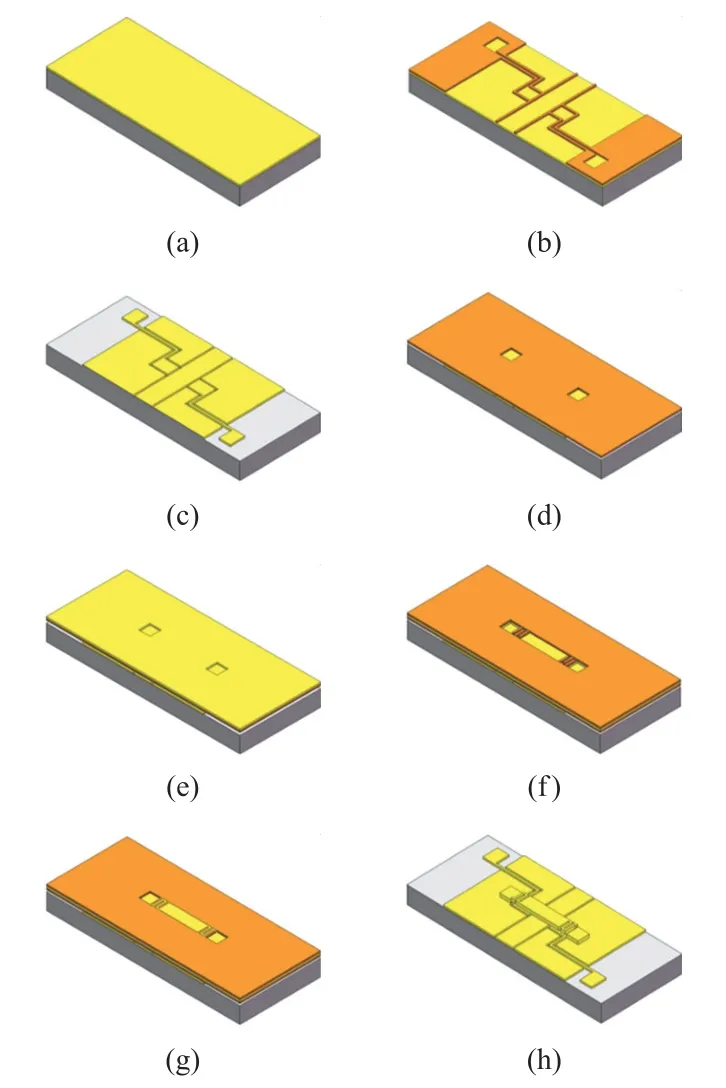
图6 双端固支梁RF MEMS开关制造工艺流程图

②涂覆光刻胶、光刻显影共面波导传输线、驱动块图案，如图6(b)所示。

③电镀金并去除未被电镀的金种子层，如图6(c)所示。

④涂覆光刻胶、光刻显影锚区图案，如图6(d)所示。

⑤溅射一层金种子层，如图6(e)所示。

⑥涂覆光刻胶，形成弹簧结构和膜桥图案，如图6(f)所示。

⑦电镀金，形成锚区和双端固支弹簧梁，如图6(g)所示。

⑧去除牺牲层，释放RF MEMS双端固支梁结构，如图6(h)所示。

加工工艺流程示意图如图6所示。

3.2 制备结果

基于3.1中的表面微机械加工工艺步骤，制备了双端固支梁结构RF MEMS开关，其SEM图如图7所示。

图7 双端固支梁结构RF MEMS开关SEM图

4 实验表征

对制备出的双端固支梁RF MEMS开关进行测试，以验证理论模型计算及仿真结果的正确性。由三维轮廓仪测得制备出的开关结构参数如表1所示。

开关相位特性的测试电路如图8(a)所示，所需要的测试仪器有:探针台和安捷伦N5244A PNA-X矢量网络分析仪，测试平台如图8(b)所示。

图8 RF MEMS开关微波特性测试电路与测试平台图

测试过程中，将制造出的RF MEMS开关分别紧贴在曲率为0(平坦)、20 m-1、22.2 m-1、25 m-1、28.6 m-1的模具上，使其产生弯曲，从而得到在不同弯曲曲率下开关的相位值，再进行数据处理，得到不同弯曲曲率下开关相位相对于平坦时开关相位偏移量，并将其与模型计算值和仿真值做对比。

图9是RF MEMS开关相位偏移实测值与仿真值和模型计算值的对比。图9(a)是在10 GHz频率下，衬底从平坦增加到曲率为28.6 m-1时开关相位偏移量的变化。在10 GHz频率下，随着曲率的增加，开关相位偏移量从0°变化到-2.72°，实测值与模型计算值的最大误差不超过7.0%，实测值与仿真值的最大误差不超过7.7%。图9(b)是在8 GHz~12 GHz频段下开关的相位偏移量，由结果可见，随着频率的增加，开关的相位偏移量绝对值不断增大，实测值与仿真值的最大误差不超过9.5%，实测值与模型计算值的最大误差不超过10.9%。误差产生原因是由于在理论模型计算过程中为了模型的简化，只考虑了平板电容、平板电感和弹簧电感，没有全面计算其他的寄生参数，导致在大曲率下的相位偏移量曲线产生偏差。同时由于制备过程中工艺的影响，双端固支梁的凹陷形状并不是一个标准的正弦曲线，但采用正弦曲线近似后的梁模型与实测情况贴合较好且误差较小，证明其可以使用正弦曲线来近似逼近实际梁的形状。

图9 衬底弯曲对RF MEMS开关相位偏移影响的实测值、仿真值与模型计算值

由实测结果分析可得，随着双端固支梁RF MEMS开关衬底曲率增加，其翘曲程度逐渐变大，导致共面波导信号线与双端固支梁之间的距离变小。由于电容与距离成负相关的关系，导致相位特性模型中等效电容变大，相位偏移量绝对值增大。同时，随着频率的增加，共面波导信号线在长度不变的情况下，微波波长减小，电长度增大，也会导致相应开关的相位偏移量绝对值增大。实测结果与软件仿真和理论模型计算结果完全一致，验证了理论模型的正确性和有效性。

5 结论

本文从理论模型、软件仿真和实际测试三个方面对不同衬底弯曲曲率下双端固支梁RF MEMS开关的相位偏移进行了深入研究，建立了柔性RF MEMS开关的相位特性模型，并对开关进行工艺制备和实际测试。模型计算值、仿真值与实测值得到的开关相位偏移趋势结果一致，证实了随着衬底曲率的增大，RF MEMS开关的相位偏移量绝对值不断增大，中心频率10 GHz处相位偏移量由0°变化到-2.72°，同时8 GHz~12 GHz频率范围内实测值和仿真值误差小于9.5%，实测值和模型计算值误差小于10.9%，三者在误差允许范围内符合的很好，验证了双端固支梁RF MEMS开关相位特性模型的正确性。