电力供应量智能分析系统总体框架设计

杜俊贤

(烟台汽车工程职业学院 电子工程系， 山东 烟台 265500)

0 引言

电力系统在经济发展中作用重大，迅速发展的经济促使各产业的发展水平及国民生活水平得到快速提升，日常生产生活对用电量的需求随之不断提高，激增的用电量需求促使电力系统整体规模不断扩大，一些新增发电项目在保障和促进经济稳步发展中发挥着重要作用。为了促进电力系统的运行稳定性，必须要保证电网供需平衡。而目前调度计划的制定需基于电力供应量及电力负荷的有效预测，准确的负荷预测是提升制定调度计划准确度的重要手段，使由预测不准确带来的弃电损失问题被有效避免。

1 需求分析

电力供应在日常生产生活中起到重要作用，随着国民经济发展对用电需求的不断提升，对稳定的电力供应提出了更高的要求，仍然存在不同程度的供需矛盾，因此需对电力供求进行科学合理的规划，并结合实际情况作出合理决策，促进经济的稳定发展。基于统计学习理论的支持向量机属于一种小样本学习算法，分类与回归分析的应用非常广泛，支持向量机回归因而在众多领域(包括粮食产量、股市、气象、电力负荷等方面的预测)得以广泛应用。电力供应量的影响因素通常表现出较大的不确定性和复杂性，在统计电力产量时通常以季度或年作为时间标度，预测电力供应量属于典型小样本的非线性问题，但是支持向量机很难对样本的特征属性进行评价，所以在对模型进行训练和检验过程中易受到一些次要属性的干扰和影响，进而影响到最终的预测精度，因此对支持向量机的优化和完善仍然是研究重点，例如，通过对输入样本的权重或特征属性进行优化处理，实现预测精准度的有效提高，在获取样本数据属性的本质关系具有较大的优势，对于知识的不确定性、信息的冗余程度具有较强的包容性，只要找到最小预测规则集即可[1]。因此本文在支持向量机回归的基础上结合运用粗糙集属性约简方法对数据样本进行预处理和预测，针对电力相关历史数据(包括产量及其主要影响因素)样本建立回归分析模型。

2 基于粗集属性约简的电力供应量智能预测

电网供需平衡是确保电力系统稳定运行的基础，目前相关超大容量电能存储技术仍处于研究阶段，随着用电需求和电力负荷的影响及制约因素的增加(如电价高低、区域经济、气候等关联影响因素)，电力系统的稳定运行需通过相应发电调度计划的有效实施实现，电力供应量及负荷预测在电力系统中起到非常重要的支持作用，电力规划及日常生产运行等工作均离不开电力供应量及负荷预测(主要是对年最大负荷及用电量进行预测)，不断增加的用电量对预测电力负荷的精准度提出了更高的要求，受到有限历史数据的限制，电力负荷受不确定因素的影响较大，通过准确的电力负荷预测可以为社会效益的稳定发展提供保障。

2.1 支持向量机回归应用原理

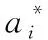
(1)

约束条件为式(2)。

(2)

针对非线性支持向量回归问题，往往会将数据通过某一非线性映射的引入实现到更高维Hilbert空间的映射，线性回归(对应原空间的非线性回归)在此空间完成。为使高维空间内点积运算的复杂程度得到有效降低，针对低维空间输入完成到高维特征空间的点积(通过核函数技术)，即K(xi，xj)=<Φ(xi)，Φ(xj)>。

对于非线性回归，其最优超平面解析的表达式[2],如式(3)。

(3)

常用核函数包括p阶多项式核函数 、高斯径向基核函数、Sigmoid核函数，对应表达式如式(4)—式(6)。

K(xi，xj)=(<(xi，xj>+c)p(p∈N，c≥0)

(4)

K(xi，xj)=exp {-‖xi，xj‖2/2σ2}

(5)

K(xi，xj)=tanh(θ+υ)

(6)

2.2 粗集和属性集相对约简在电力供应量智能预测中的应用

实际在对样本数据采用粗集理论进行分析时，通常以决策表作为处理对象。

(1) 决策表的定义：由知识表达系统构成决策表，其信息表具体由四元组构成表达式为S=(U，A，V，f)，U(非空有限对象集) 表示论域；V的集合由属性a∈A的值域构成;A(非空有限属性集)取值为C∪D;C表示条件属性集;D(非空集) 表示决策属性集;f表示信息函数各对象在指定论域U中各属性的取值(U×A→V)。在D仅有一个决策属性{d}的情况下则为单一决策表。

(2) 上 、下近似集的定义：对任意XU及其上由B表示的等价关系，X在此关系下的上 、下近似集定义表达式如式(7)、式(8)。

B-(X)={x|x∈U∧ [x]B∩X≠Ø}

(7)

B-(X)={x|x∈U∧ [x]B⊆X}

(8)

X在B-(X)同B-(X)取值不同的情况下称为一个B粗集。

(3) 正域的定义：由P、Q表示U上的两个等价关系，定义Q的P正域表达式如式(9)(即以U|P的信息为依据能够完成到Q的等价类中开集的集合的准确划分)。

POSP(Q)=UX∈U|QP-(X)

(9)

(4) 约简的定义：设论域U上的两个等价关系簇由P、Q表示，∀r∈S、POSS(Q) =POSP(Q)且POSS /{r}(Q) 同POSS(Q)的取值不同则S⊂P是P的Q独立子集，满足S是P的Q约简的条件[2]。

各属性在决策表信息系统中均与某个等价关系相对应，对于论域样本上的论域通过使用条件属性集和决策属性集完成划分及对应分类知识 的形成，对于条件属性集则通过运用属性约简实现部分必要属性的获取，这部分必要属性的分类能力不同于决策属性同全部条件属性相同。假设，S=(U，A，V，f)表示决策表;U表示论域取值为{x1，x2， …，xn}；A=C∪ {d}，[ mina，maxa]表示属性a(aA是一个连续属性) 的值域。粗集理论的处理对象适用于离散属性，在决策表含有连续属性的情况下需进行离散化处理，本文使用凝聚层次聚类法完成离散化处理过程使负荷预测的精准度得到显著提高，根据定义(4)完成C(条件属性集合) 的约简的获取，由Cred表示C的相对约简即C的最大独立子集(相对于决策属性{d})[3]。

3 电力供应量数据准备与预处理

电力供应量会受到生活水平、经济水平等多种因素的影响，本文选择电力产量(亿千瓦小时)、国内生产总值(亿元)、第一产业、第二产业、第三产业(亿元)、人均国内生产总值(元 / 人)、原油产量、生铁 产量、铁路货运量(万吨)、原煤产量(亿吨)因素作为代表，分别由d、a1、a2、a3、a4、a5、a6、a7、a8、a9表示[4]。

根据实际需要选取某一时间段的电力供应量的历史数据进行处理，主要步骤如下。

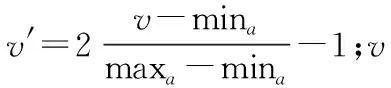
4 支持向量机回归结果与分析

通用MATLABSVMToolbox的使用完成对支持向量机回归的处理过程，核函数为K(xi，xj)=exp{-‖xi，xj‖2/2σ2}； 以线性ε-insensitive 函数作为损失函数，表达式为L(f(x)，y)=max(0， |f(x)-y|-ε)[6]。通过交叉验证确定参数C，σ，ε的选择。将原样本上述步骤(4)和(5)进行处理以便后续比较。两种回归的相关参数和结果,如表1—表3所示。

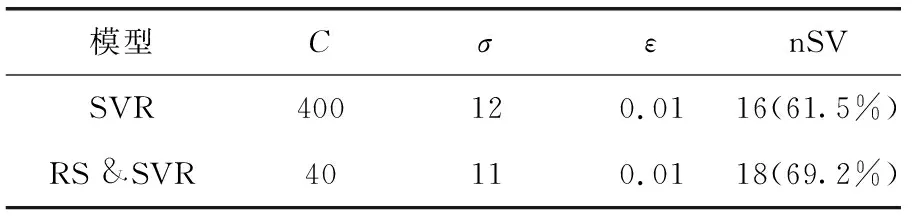
表1 参数值和支持向量个数

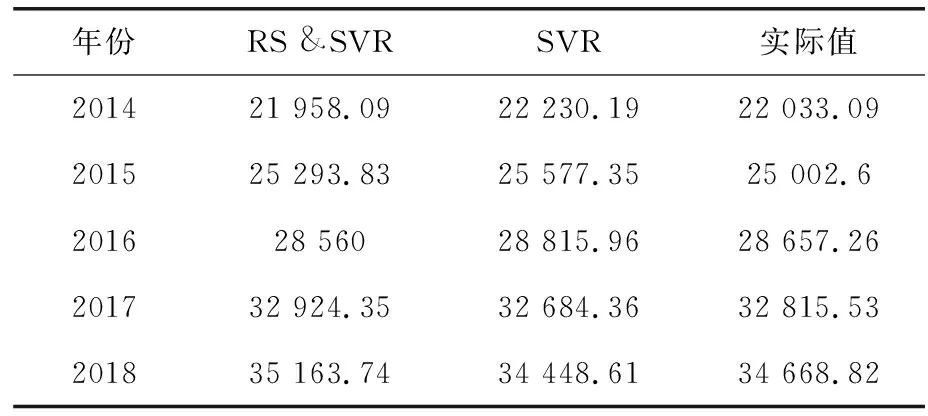
表2 电力产量预测值与实际值

表3 模型预测精度比较

其中,RMSE为式(10)。

(10)

THEIL_IC为式(11)。

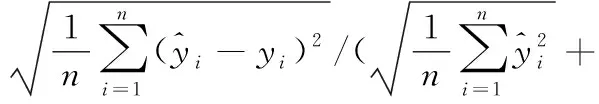
(11)

取值范围通常在 0—1之间的希尔不等系数同预测精度成反比，即希尔不等系数越小精度越高，如式(12)。

(12)

通常在MAPE的值不超过10 的情况下表示预测精度较高，如式(13)。

(13)

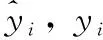
本文的RS &SVR 模型在支持向量个数方面类似于SVR模型，仅多了两个支持向量。由表2—表3可知， RS &SVR 模型的希尔不等系数以及均方根误差更小，预测值更加接近实际值，说明拟合效果及预测效果良好，充分证明了本文所构建模型应用于电力供应量回归预测过程的有效性，在满足用电需求、降低发电成本及确保电网安全稳定运行中具有较高的实用性[7]。

5 总结

在对电力供应量进行分析过程中采用支持向量机回归能够构建起较为理想的预测模型，而在对不确定的、冗余的信息进行处理时粗糙集理论表现出了强大的优势，通过在数据预处理过程中使用属性约简方法可使电力相关数据样本的特征维得到有效简化。结合运用支持向量机回归同粗糙集理论间构建的RS&SVR模型使电力供应量智能预测效果得到显著提升，使用属性约简算法完成约简处理，将电力供应量的预测结果同实际情况进行实验对比，本文基于属性约简方法构建的预测模型能够对较少的主要预测因子的信息进行充分利用， 预测结果的精准度得到显著提高。