不同工况下圆形隧道开挖模拟研究
2021-09-28薛丹丹
薛丹丹
(山西工程职业学院,山西 太原 030009)
随着社会经济发展水平不断地提高,隧道工程建设也在不断地发展,与此同时相关的问题也在不断出现。隧道开挖是一个在时间和空间上不断变化的复杂过程[1],国内外诸多学者都对其工程及围岩的稳定性进行过研究。
秦康、袁伟泽、徐干成[1]等采用理论分析和数值计算的方法对不同跨度下隧道的围岩变形、应力分布以及塑性区范围等指标进行了对比分析,得到了隧道拱顶沉降、水平收敛的拟合公式。吴波等人[2]依托深圳某隧道区间,用有效应力分析来建模,模拟隧道实际的动态开挖过程,获得了地表沉降值曲线的动态变化;中南大学的李曙光[3]依托南京地铁某区间隧道开挖,使用3D数值模拟的方法,讨论了不同的埋深、支护压力等原因对地表沉降产生的变化。
本文将理论分析和数值模拟这两种方法有机结合起来,分析隧道在仅受自重、开挖和支护三种工况下的塑性区分布、围岩变形及应力集中情况,得出隧道在不同工况下的变形规律。
1 建立模型
1.1 模型参数
1.1.1 几何参数
如图1所示,某圆形隧道内径为5.8 m,外径为5.8 m,衬砌厚度为0.28 m,埋深为12 m。按照原有的计算经验及隧道开挖的影响范围,本文选取隧道外径的3倍作为其左右边界,即17.4 m;取隧道外径的1.5倍为隧道底部至模型下边界的距离,即8.7 m。因此整个计算模型宽40.6 m,高26.5 m[4]。
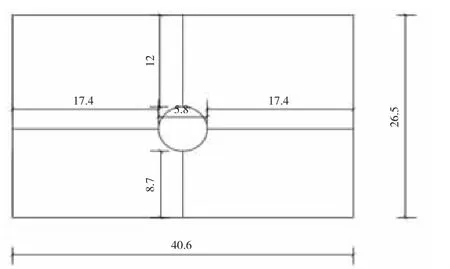
图1 圆形隧道示意图(m)
1.1.2 材料参数
隧道材料选用摩尔-库伦模型(Mohr-Coulomb Model),该模型一般适用于普通土壤和岩石的力学行为(如边坡稳定和地下开挖等)的隧道围岩;圆形隧道开挖部分选用空模型(Null Mode),该模型适用于后阶段的开挖或孔;隧道衬砌结构采用C30混凝土。
在FLAC3D中需要的材料参数有两组,一组为弹性变形参数,即所需的材料参数有:密度ρ、弹性模量E、泊松比v、体积模量K及剪切模量G;另一组为强度参数,即所需的材料参数有:内聚力c、内摩擦角φ、抗拉强度σt,如表1所示[5]。

表1 材料物理力学参数
在FLAC3D中,常用常量K和G,而不用弹性模量E和泊松比ν。它们之间的关系如下[6]:

1.2 边界条件
对模型的四个侧面(X和Y方向)进行法向位移约束,底面全约束,以保证竖直方向自由沉降。即约束X=20 m、X=-20 m、Y=0 m、Y=1 m、Z=-12 m面上所有点的位移和应力。隧道开挖后无边界条件的约束,允许其变形。
2 模拟结果与分析
2.1 隧道仅受自重的影响分析
由图2可知,隧道在仅受自重时,围岩下方塑性区面积较大,字母“n”的单元体表示现在正在被破坏;字母“p”表示的区域内其中隧道附近中心区域发生剪切破坏,紫色塑性区部分表示过去受到张拉破坏。

图2 隧道仅受自重时的塑性区分布
由图3和图4可以看出,在自重应力场下,由于隧道附近区域单元大小不一,故竖向位移和应力分布有轻微变化,其余部分的竖向位移和应力(分布较均匀)呈水平条状分布。由于未进行开挖,全部单元均处于弹性状态,围岩出现初始沉降现象。

图3 隧道仅受自重时的竖向位移(m)分布

图4 仅受自重时的竖向应力(Pa)分布
2.2 隧道开挖数值模拟分析
由图5可知,隧道开挖后,附近围岩受到不同程度的破坏。拱顶和隧道底部区域主要显示为“tension-p”状态,主要表现为过去受到张拉破坏,左右拱脚区域有受拉和剪切塑性区出现。

图5 开挖后的塑性区分布
由图6可知,最大主应力出现在隧道顶部,大小为9.98×103Pa,方向向上,受到拉应力。此时隧道开挖打破了隧道主应力的均匀分布状态,拱顶周边出现了较大的应力集中现象。隧道开挖部分的拱顶、侧墙、拱脚及底板是应力集中程度较大的位置,拱顶及其附近表现为拉应力,不利于围岩的稳定性;拱脚和侧墙区域表现为压应力。如果隧道围岩自身具有较大裂缝或由于爆破产生较大裂缝,就会导致不稳定体发生冒落,引起整个隧洞的损坏。

图6 开挖后的最大主应力(Pa)分布
由图7可知,隧道开挖后最大竖向位移发生在拱顶处,为-1.05×10-2m,负号表示方向向下,主要由于该处受到上部土体的自重作用,故发生下沉;隧道底部中心区域竖直位移为9.56×10-3m,方向为正,表现为向上隆起。

图7 开挖后竖向位移(m)分布
由图8可知,最大水平位移发生在左右拱脚处,均为6.33 mm,方向相反。在这里水平位移分布沿着周边逐渐衰减,且沿深度发生一定扩展,左边显示为红色区域,方向为正,右边显示为蓝色区域,方向为负,即隧道水平方向整体指向隧道中心。

图8 开挖后水平位移(m)分布
综合以上分析可知,沿隧道轴线方向的分布,水平方向的变形要比竖直方向均匀的多,即表示水平变形小于竖向变形。隧道开挖前后,由于周边应力解除,范围内的部分岩体发生变形,并向隧道内移动,继而使得岩体中的初始应力也发生相应变化,且应力得到重分布。
2.3 隧道支护的竖直模拟分析
由图9和图10可知,隧道支护后周围无剪切破坏和张拉破坏,即拱顶和底部显示蓝色区域,表示为tension-p状态,即过去受到张拉破坏;侧墙和拱脚处显示仅过去受到剪切破坏和张拉破坏,即隧道此时不受破坏,处于稳定状态。最大主应力仍发生在拱顶区域,为1.24×104Pa,方向为正,表示受到拉应力。

图9 支护后的塑性区分布图

图10 支护后的最大主应力(Pa)分布图
由图11可知,隧道支护后,竖向最大位移发生在拱顶处,为1.17×10-2m,方向向下。由于围岩的局部发生失稳和破坏现象,使得隧道的边界条件发生变化,二次应力得到重分布,二次强度重新变化,继而使得新的区域发生局部失稳和破坏现象。即变化过程一般为破坏—变化—平衡—再破坏—再变化—平衡,因此在工作中要及时进行人为支护,确保其处于稳定状态,并采取一定的安全措施,以防围岩应力发生重分布现象。

图11 支护后的竖向位移(m)分布图
由图12可知,隧道支护后,水平最大位移发生在左右拱脚区域,为6.21×10-3m,表明开挖后及时对隧道支护,可以有效防止变形。隧道支护后,周围岩体的能量部分被释放、部分转移到支护上、部分转换到深部区域的围岩上,使得围岩变形受到一定程度的约束,即变形速度逐渐减慢。又因为对衬砌的混凝土进行了柔性支护,支护刚度得到提高,因此也允许围岩有一定变形的发生。

图12 支护后的水平位移(m)分布图
3 不同工况条件下的隧道结果分析
在本文研究条件下,选取隧道仅受自重、开挖及支护三种不同工况作为研究对象,在这里由于隧道未开挖时处于稳定状态,故仅选取隧道开挖及支护两种工况,进行分析。具体数值结果如表2所示。

表2 不同工况下隧道的变化值
计算结果显示:隧道开挖后及时支护,有利于提高隧道围岩的稳定性。但仅仅依靠初期支护不足以达到对围岩稳定性的要求,而极有可能引发隧道发生局部冒顶和片帮现象,致使隧道局部发生破坏,继而对施工人员的人身和财产安全造成威胁,甚至会不利于隧道整体的稳定性,因此在后期,仍要持续观察,对其不断进行加固和支护,确保长期的稳定安全。
4 结论
本文采用FLAC3D有限元软件较好地模拟了隧道开挖及支护的全过程,分别对隧道开挖前仅受自重、隧道开挖及支护这三种工况,进行了分析计算,得到了开挖前后及支护状态下的塑性区、最大主应力、竖向位移与水平位移的分布规律。具体结果如下:
1)从隧道开挖前后的水平方向及竖直方向位移变化可以看出,水平方向相对于竖直方向要稳定许多。
2)隧道开挖对竖直方向的变形影响较大,随着隧道地不断开挖,可能会影响到地表稳定性,在隧道拱顶和拱肩部区域会出现应力明显集中的现象,但是对拱脚和侧墙的影响较小。
3)根据隧道开挖前后的最大主应力分布可以得出,隧道在开挖后及时进行支护可以有效预防冒顶或片帮现象的发生,从而保证施工人员的安全及隧道的整体稳定性。
