基于社交媒体数据的贝叶斯A/B 检验
2021-09-28李薛莎付英姿夏思琴
李薛莎,付英姿,薛 茜,夏思琴
(昆明理工大学 理学院,云南 昆明 650093)
0 引言
A/B 检验主要用于考察相对于原方案A,改进方案B 是否更优。其基本思想是从包含实验组和对照组的平行实验中收集数据,并利用检验手段评估两个方案中哪一组成功率更高,从而帮助决策者作出科学判断。目前,A/B 检验已被广泛应用于生物医学、药学、心理学、社会行为学等多个领域。例如,医药公司常常利用A/B 检验考察所研发的新药相较于传统药物,在疗效方面是否更显著。此外,A/B检验还可用来衡量心理干预是否能够加快促进病人痊愈。在大数据背景下,社交媒体数据蕴含着巨大的商业价值,A/B 检验已被成功地运用到商业网站点击率预测以及精准营销方案的投放等多个应用场景,然而从国内外相关研究成果看,大多数研究还处于起步状态。由此可见,对A/B 检验问题的研究有着巨大的探索空间和价值。
在经典的假设检验问题中,A/B 检验可以理解为关于零假设的显著性检验(Null Hypothesis Significance Testing,NHST),其相应的p值表示样本在原假设下出现极端事件的概率,即观测到的显著性水平。当p值小于规定的显著性水平α时,则拒绝原假设;否则,接受原假设。随着研究的深入,人们发现经典的检验方法存在诸多局限性,例如,Wagenmakers[1]研究表明,基于p值的假设检验存在逻辑和统计限制,它易受主观意图的影响,不能很好地量化统计证据;Gallistel 等[2]、Rouder 等[3]进一步指出,基于p值的经典检验方法依赖于未观察到的数据,难以对原假设提供足够的支持。为此,Malek 等[4]对基于p值的经典检验方法作出改进,使其能够随着数据的增加而自动进行校正,更多相关研究成果可参见文献[5-7]。
众所周知,贝叶斯方法的优势在于它能够借助于优良的先验信息以提高检验精度,同时对样本量没有过多的限制。从贝叶斯的角度看,贝叶斯A/B 检验的关键是比较两种方案下后验概率的大小,其本质是通过引入贝叶斯因子以实现模型间的比较和选择。早在1935 年,Jeffreys[8-9]率先提出用于标准假设检验问题的贝叶斯因子,这为贝叶斯A/B 检验奠定了基础。随后,Kass 等[10-11]改进了Jeffreys 所提出的近似贝叶斯因子的方法,并将其应用于两个二项式比例相等性的检验问题上;Alexander 等[12]研究了两个常见的基于贝叶斯因子假设检验的应用场景,即检验正态均值的零度(即贝叶斯t检验)和检验相关性的零度问题,并将其应用于心理学实验。然而,从现有研究成果看,目前大多数研究仅考虑了两个方案下成功概率是否相等的问题,还难以确定出最优方案。为此,本文拟考虑如下3 类假设检验问题,即:①H0:P1=P2,H1:P1≠P2(两个方案是否相等);②H0:P1=P2,H+:P1
网页改版能否带来更多点击率,从而为公司带来更大利润一直都是网络公司关注的核心问题。为此,本文以硅谷前沿科技教育平台优达学城(Udacity)提供的新旧版本网页点击转换率数据为例,建立了基于贝叶斯因子的A/B检验并挑选出最优方案。具体地,首先建立贝叶斯框架下的二元Logistic 回归模型以刻画网页改版前后的点击率;在后验概率的比较方面,其关键在于贝叶斯因子的计算,注意到贝叶斯因子是不同假设下边际似然函数的比值,问题就进一步归结为边际似然的计算。为此,采用拉普拉斯近似方法解决上述问题,特别地,对于单边假设(II)和(III)而言,本文在拉普拉斯近似的基础上增加了重要性抽样技术以更好地拟合尖峰厚尾分布。研究结果表明,对网页的改版并不能有效地增加用户点击率。
1 模型与方法
1.1 假设检验问题提出
假设有两个方案A 和B,方案A 表示原方案,方案B 则是对A 作出某些改进或调整后形成的新方案。令p1为方案A 的成功率,p2为方案B 的成功率。A/B 检验的目的是考察新方案对于原方案而言,在成功率上是否有所提高,与之对应的假设检验问题为:原假设H0:P1=P2,备择假设H1:P1≠P2。若接受原假设,则认为A、B 方案没有区别;否则,认为两个方案有区别。注意到,上述假设检验问题仅关注了A、B 方案是否等价,而无法确定哪一个方案更优。为此,本文在经典检验问题的基础上又引出如下两个单边检验问题,分别为:H+:P1
1.2 二项分布与Logistic 回归
在具体实施过程中,A/B 检验从包含实验组(A)和对照组(B)的平行实验中收集数据,并根据样本计算出不同方案下的成功率以确定最优方案。假设Y1为方案A 下的成功次数。显然,Y1服从成功率为P1的二项分布,即其中N1表示方案A 的实验总次数。同理,假设Y2为方案B 下的成功次数,即其中N2表示方案B 的实验总次数。对于二项分布而言,Logistic 回归是刻画二项分布中成功概率P的通用选择。为此,本文考虑如下典则联系函数
经典的假设检验问题需要比较两个方案在成功率上是否相等,即需要考察假设检验问题H0:P1=P2,H1:P1≠P2,注意到:
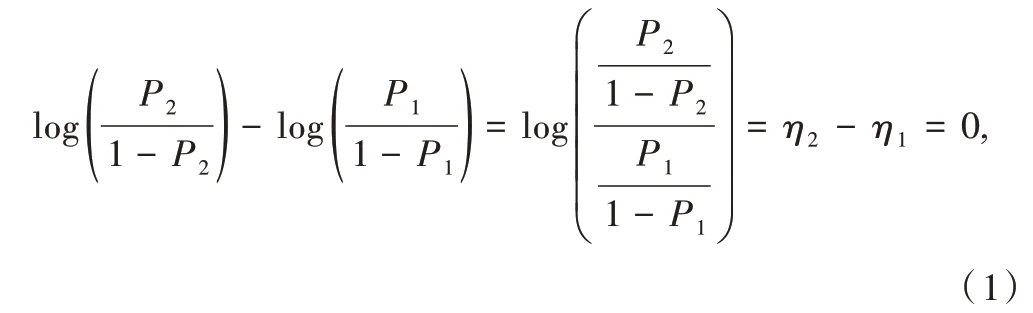
可见,原假设检验问题与检验H0:η2-η1=0,H1:η2-η1≠0 是等价的。进一步地,若令ψ=η2-η1,原假设检验就退化为检验ψ是否为0 的问题。为了检验两个二项式比例是否相等[11],可构建二元Logistic 回归模型如下:
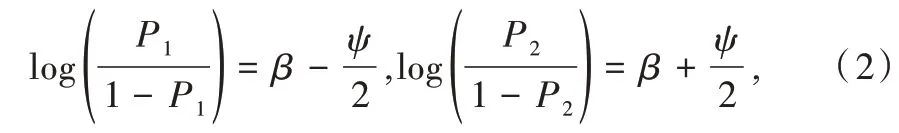
结合式(1)、式(2)则有:
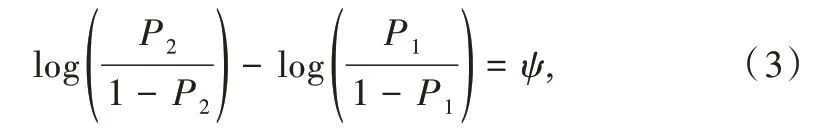
①H0:P1=P2,H1:P1≠P2→H0:ψ=0,H1:ψ≠0;
②H0:P1=P2,H+:P1
③H0:P1=P1,H-:P1>P2→H0:ψ=0,H-:ψ<0。
1.3 基于贝叶斯 检验的后验推断
1.3.1 贝叶斯因子及边际似然计算
在贝叶斯框架下,贝叶斯因子[13](Bayes Factor)量化了数据对原模型和备选模型的支持程度,是模型比较和选择的重要统计量。其定义为:对于两个模型H0、H1,其中H0表示原模型,H1表示竞争模型,假设数据集Y来自于H0、H1中的其中一个,分别对应于边际似然函数:和则有:
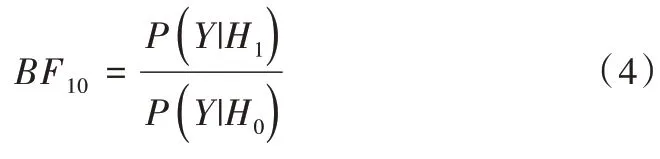
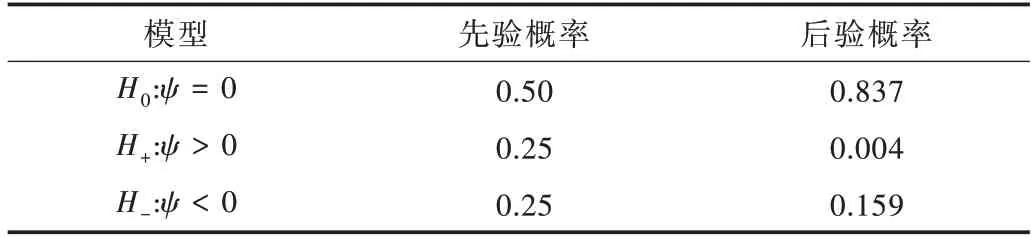
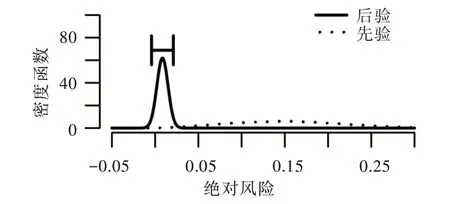
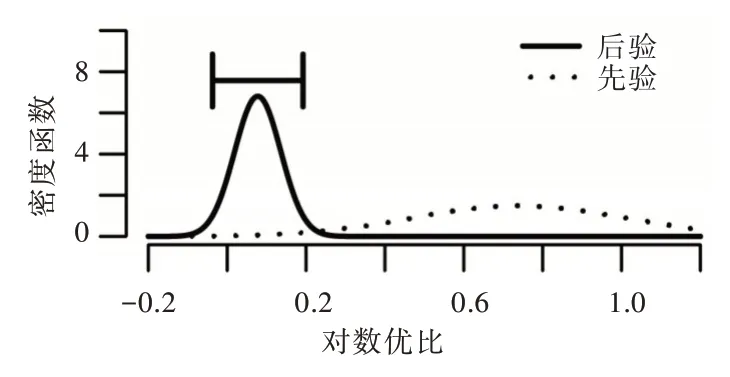
其被称为用于比较原模型H0和备择模型H1的贝叶斯因子。对于贝叶斯因子的解释,一般认为,当BF10<1 时,表明有证据支持原模型,即H0优于H1;当1 针对本文考虑的3 类假设检验问题:①H0:ψ=0,H1:ψ≠0;②H0:ψ=0,H+:ψ>0;③H0:ψ=0,H-:ψ<0。其 对应的贝叶斯因子分别为: 如上所述,A/B 检验关注的是新方案相对于原方案是否有所改进。从贝叶斯的角度看,问题归结于考察上述3类假设检验的后验概率是否有所提升的问题。由贝叶斯定理可知,后验概率比即后验似然比与贝叶斯因子之间存在如下关系: 其中,P(Y|H0)表示原模型的边际似然函数,表示备择模型的边际似然函数。 本文分别给出了3 类假设检验问题下贝叶斯因子的具体表达式: (1)考虑H0:ψ=0,H1:ψ≠0,贝叶斯因子为: (2)考虑H0:ψ=0,H+:ψ>0,贝叶斯因子为: (3)考虑H0:ψ=0,H-:ψ<0,贝叶斯因子为: 1.3.2 拉普拉斯近似 由式(5)可知,后验似然比由贝叶斯因子和先验似然比两部分构成,而先验似然比通常事先指定,于是问题的关键就归结为如何计算贝叶斯因子。由式(6)—式(8)可知,贝叶斯因子定义为两个竞争模型的边际似然函数的比值,其计算涉及难以处理的复杂积分。为此,本文将采用拉普拉斯近似[14-15](Laplace Approximation)的方法解决复杂积分求解问题。 拉普拉斯近似的基本思想是将难以求解的积分问题转换为正态分布形式,以降低复杂积分求解难度。这种近似方法适用于被积函数是单峰时的情形,以确保拉普拉斯近似逼近收敛到唯一一个最大值。众所周知,泰勒展开可以通过一个点对函数进行观察,基于此,拉普拉斯近似通过对被积函数在众数点(mode)的邻域内进行二阶泰勒展开以近似积分,更多拉普拉斯近似的相关细节可参考附录。 针对情形(1),考虑假设H0:ψ=0,由于在H0下模型只含有参数β,根据拉普拉斯近似有: 考虑备择假设H1:ψ≠0,此时模型中含有两个参数待估参数β和ψ,类似地,根据拉普拉斯近似有: 基于式(9)、式(10),可计算得到贝叶斯因子BF10,接下来将考虑BF+0和BF-0的计算问题。 1.3.3 重要性抽样 显然,单边假设H+是下界为0 的截尾正态分布,H-是上界为0 的截尾正态分布,此时若继续使用拉普拉斯近似方法,将会导致有偏甚至无效的统计推断结论。为此,本文引入重要性抽样[16-17]近似表示H+和H-下的边际似然函数。 重要性抽样突显了被积函数中重要区域的贡献,是蒙特卡洛方法(Monte Carlo,MCMC)中最有效的方差缩减技术。其主要思想是利用一个分布较简单的函数(重要性密度函数)中大量样本点的加权平均以近似积分过程。在模型H+、H-下分别令经验表明,当多元t分布的自由度为5 时,对于尖峰厚尾的分布具有良好的拟合效果。因此,本文选取自由度为5 的多元t分布作为重要性密度函数。 针对情形(2),由于模型H0边际似然函数在式(10)已计算出,因此只需计算模型H+的边际似然函数,其近似结果为: 本文利用重要性重抽样(SIR)方法获取后验样本,基本思想是在重要性抽样函数中抽取样本,通过加权修正抽样概率,使样本中的每个观测点依据概率再次抽样,从而获得后验样本。具体步骤如下: (1)产生样本。从给定参数的多元t分布函数tin中抽取N个独立同分布的样本β(n)、γ(n),其中n=1...N。 (2)计算重要性权重: (4)重采样及算法监控。使每一个观测点以概率vn出现在N个样本中,同时有放回地重新抽取样本,直至的分布收敛到目标后验分布。在收敛性方面,本文采用EPSR(Estimates Potential Scale Reduction)值以监控算法收敛情况。 针对情形(3),由于模型H0边际似然函数在式(10)已给出,只需计算模型H-下的边际似然函数,其近似结果为: 模型H+和H-对应的边际似然函数近似计算结果如式(11)、式(13)所示,结合模型H0的边际似然函数近似结果,可分别计算出贝叶斯因子BF+0和BF-0。 1.3.4 先验设置 如上所述,当β和ψ为零正交参数时,β不同的先验设置对贝叶斯因子影响很小。然而,ψ反映出备择假设与零假设之间的差异,因此对ψ的先验设置至关重要。本文对参数β和ψ均考虑正态先验,对于参数β,其先验设定为标准正态分布,即β~N(0,1) 。对于模型H+:ψ>0,参数ψ的分布是一个下界为0 的截尾正态分布,而对于模型H-:ψ<0,ψ的分布是一个上界为0 的截尾正态分布。因此,本文考虑为了得到超参数μψ和σψ的具体取值,考虑如下最小二乘法(Least-squares minimization)以估计参数μψ、σψ。 其中,qi,i=1,...I表示分位数,pi,i=1,...I表示分位数对应的概率值表示参数ψ的先验累计分布函数,更多计算细节可参考文献[18]。 基于贝叶斯因子,结合先验概率比,可计算出后验概率比。由于贝叶斯方法具有内在一致性,即上一步的后验可作为下一步的先验,通过考察不同先验设置下后验概率的变化情况,可以量化数据对不同竞争模型的支持程度,从而进行模型与方案之间的选择。 本文利用硅谷前沿科技教育平台优达学城(Udacity)提供的新旧版本网页点击转换率数据为例,说明本方法的适用性。该公司在旧版网页的基础上开发了一款新的网页,将新版网页投放到客户端,尝试增加用户点击率,期望让更多的用户愿意为产品付款,同时帮助公司了解实施新方案能否增加公司效益。该数据集共包含10 000 个样本点,涉及旧版网页(Old Page)点击转换率、新版网页(New Page)点击转换率,记方案A 表示公司采用旧版网页,方案B 表示公司采用新版网页,并将用户成功跳转网页并付款的事件记为“1”,反之记为“0”。 本文选取5 000 个实验组使用旧版网页,5 000 个对照组使用新版网页,记录每组中用户的页面使用情况。公司感兴趣的是网页改版能否增加点击率,从而给公司带来利润。假设公司预期使用新版网页点击率提高15%,这里的15%对应着绝对风险的先验中位数,其置信水平为95%的置信区间为[0.025,0.275]。本文为参数β、ψ分配正态分布先验。如上所述,参数β先验的改变对贝叶斯检验结果影响不大,因此考虑将其设置为标准正态分布,即β~N(0,1),而参数ψ反映出备择假设与零假设之间的差异,故ψ的先验设置至关重要。Howard 等[19]表明当成功概率P1非常(小)大时,成功概率P2也会非常(小)大,且二者具有相互依赖的关系。在此基础上,本文同样考虑,并使用最小二乘法估计超参数μψ、σψ,考虑取q=(0.025,0.15,0.275),则对应的概率值p=(0.025,0.5,0.975),结合式(14)利用最小二乘估计计算出先验设置结果如表1 所示。 Table 1 Results of prior setting表1 先验设置结果 由上述分析可知,方案A 与B 相等、方案B 优于A、方案B 劣于A 分别对应于假设检验问题H0:ψ=0、H+:ψ>0、H-:ψ<0。不失一般性,将先验概率的初值赋为贝叶斯因子的计算结果分别为BF10=0.011,BF+0=0.01,BF-0=0.379,均小于1,表明有证据支持零假设,即P1=P2。根据计算出的贝叶斯因子,在给定先验概率的情形下,计算出不同假设模型下的后验概率,结果如表2 所示。 Table 2 Posterior probabilities of different models表2 不同模型下的后验概率 通过表2 可以发现,模型H0:ψ=0(p1=p2)的后验概率较先验概率提升较明显,概率由0.5 增长到0.837,模型H+:ψ>0(p1 观察表3 可以看出,P1的估计值为0.120,P2的估计值为0.129,二者差距不明显,数据表明支持零假设H0:ψ=0,即P1=P2。因此,有理由认为改进后的网页并不能给公司增加预期点击率及利润回馈,但实际上存在这样一种可能,即新版网页确实能够增加网页点击率,但是改善效果并没有公司预期高。为了评估这种可能,本文利用贝叶斯绝对风险度量这种可能性,结果如图1 所示。 Table 3 Results of parameter estimation表3 参数估计结果 Fig.1 Absolute risk图1 绝对风险 其中,后验中值为0.008,95%的置信区间为[-0.004,0.021]。从图1 可以看出,在两个成功概率的差值不完全为0 的情况下,绝对风险的后验中值小于先验中值。因此,可以认为对网页进行改版确实可以增加网页点击率,但是改善的效果远低于公司预期。 由此可知,参数ψ表示对数优比,它可以反映出其他假设与零假设H0之间的差异程度。为了进一步证实改版网页对增加点击率是否有效,本文绘制出关于参数ψ(对数比值比)的先验分布与后验分布图像,如图2 所示。 Fig.2 Log odds ratio图2 对数优比 其中,后验中值为0.078,95% 的置信区间[-0.038,0.195]。从图2 可以看出,对数优比的后验分布中值小于先验分布中值。可以看出,Udacity 平台推出新网页后,对网页点击率有一定促进作用,但是低于公司预期。因此,公司可以考虑不对网页进行更换。 本文以硅谷前沿科技教育平台优达学城(Udacity)提供的新旧版本网页点击转换数据为例,通过构建完整贝叶斯框架下的二元Logistic 回归模型与后验模拟算法对新旧版本网页点击率进行A/B 检验。研究结果显示,公司改版后的网页对于增加点击率从而增加公司收益的作用并不明显,因此对于网页更换可以酌情考虑。针对不同的领域,该方法可以应用于医疗行业、心理学行业等,以帮助解决实际问题。本文主要研究了贝叶斯框架下A/B 检验在商业方面的应用及推广,其研究成果对于企业网页改版具有重要参考价值及指导意义。然而,本文仅考虑了基于两组方案数据(A 组和B 组)的贝叶斯A/B 检验,事实上,为了考虑更多的可能性,通常需要比较两个以上的方案,从而选择其中最优的一个方案。例如,当实验方案组别增加至3组时(A 组、B 组、C 组),可以使用贝叶斯损失函数衡量不同方案成功概率的大小,从而选择最优方案[20]。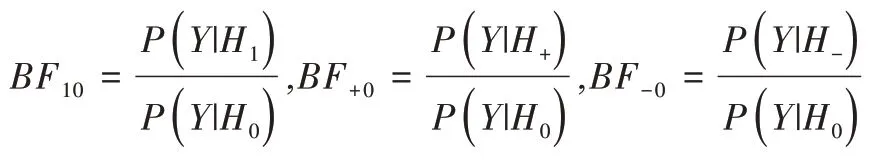

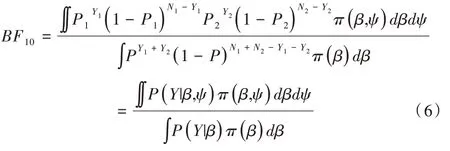
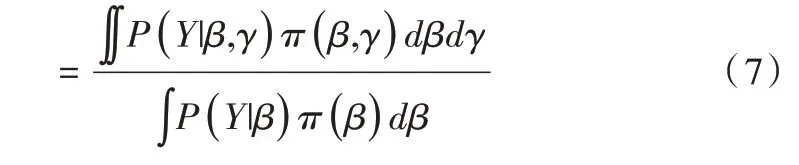
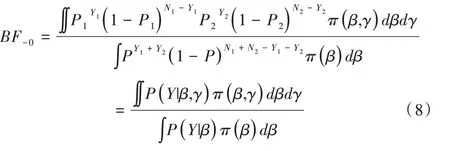



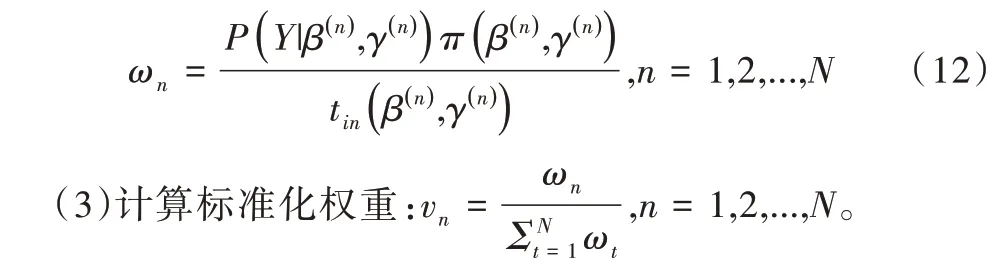
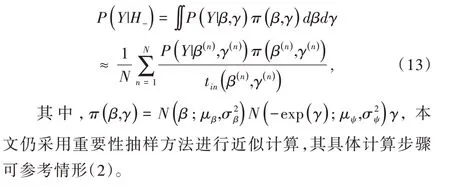
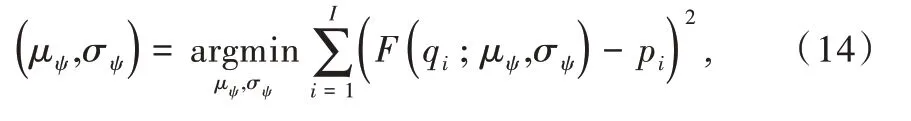
2 实例分析

3 结语
