一种分组模式下的土壤重金属含量预测模型

吕鑫涛，张 聪，曹文琪

（武汉轻工大学数学与计算机学院，湖北武汉 430023）

0 引言

土壤是人类生活、社会发展和自然进化的重要资源。要改善地球生态环境和人类生活环境，对土壤进行整治必不可少，但土壤中的重金属是非常棘手的一种污染物，难以被微生物降解，影响农作物生长，导致农作物产量下降；通过人体接触或食用最终进入人体，影响健康［1-5］。因此，对土壤重金属进行研究成为环境污染研究的重要内容之一。

土壤重金属含量预测研究提出了多种预测模型，对土壤属性作了相关分析，如陈飞香等［6］以广东增城市为例，采用随机采样方法对土壤中Cr 的含量进行分析，通过RBF 网络对Cr 含量插值进行预测误差分析，证实RBF 网络插值方法克服了克里格插值的平滑效应，有更好的预测效果；Ser⁃geev 等［7］提出一种人工神经网络（ANN），模拟非线性大规模趋势，用统计方法对残差建模预测土壤重金属，证实神经网络预测重金属空间分布的可行性；张钰等［8］将新疆克拉玛依人工碳汇林作为采样区域，通过BP 神经网络和GIS技术建模，对土壤中Cu、Zn、Fe 等5 种金属含量的分布进行分析，证实双隐层BP 神经网络能够满足预测精度并能分析土壤中重金属含量的空间分布；杨勇等［9］用时空克里格模型对武汉市青山区土壤中重金属含量在时间和空间进行了建模预测，在土壤污染防控治理问题上具有参考作用；吕杰等［10］以陕西金堆城矿区尾矿库为例，通过实验室化学分析和小波神经网络对土壤中Cu 的含量进行了分析，利用ASD 光谱仪的遥感数据对土壤重金属做出评价，证实小波神经网络反演土壤Cu 元素含量的有效性；Cao 等［11-12］以小波神经网络和径向基神经网络为主分别提出了协同复合神经网络模型和深度复合模型，通过对神经网络的初始权值与阈值进行优化，并且对土壤重金属含量进行预测分析，提升了模型的预测精度；Eid 等［13］运用污水污泥（sew⁃age sludge）改良过的土壤种植作物，可以提高模型预测的准确性。黄赵麟等［14］构建了源汇模型（BP-S）、空间分异模型（BP-K）和改进的多因素综合模型（BP-SK）模拟预测了5 种重金属Cd、Pb、Cr、Cu 和Zn 含量，证实了BP-SK 模型在人为干扰大的区域中重金属空间分布预测比BP-K 模型更实用；Zahida 等［15］对卡拉奇城市土壤进行污染评价，利用累积频率分布（CDF）曲线估算了重金属地球化学基准浓度；Pandit 等［16］通过偏最小二乘法（PLSR）建立模型反映土壤重金属含量与高光谱反射率之间的关系，证实光谱反射率在反演Pd 等重金属浓度时有着较高的预测精度，也说明光谱反射技术能够绘制重金属的空间分布；Vinod 等［17］用了回归建模，主成分分析（PCA）和积累营养成分（ANE）方法对综合工业废水灌溉土壤重金属进行分析，提出了以土壤pH 值和重金属含量作为自变量的模型。上述对土壤重金属环境污染进行评估，以及对土壤时间和空间特征分布的研究都取得了不错的预测效果。本文提出一种基于分组教学优化算法［18］（Group Teaching Optimization Algorithm，GTOA）和BP 神经网络预测模型，能够有效避免BP 神经网络在训练时收敛过慢问题，提升预测精度。

1 基础理论

1.1 分组教学优化算法

分组教学优化算法相较于传统的智能优化算法，最显著的特点是需要调整的参数很少，只有种群大小以及迭代次数两个参数，这种少量参数设置能极大发挥算法的优化性能。算法流程主要分为能力分组阶段、教师教学阶段、学生学习阶段、教师分配阶段。

（1）能力分组阶段。对于一个班级的知识分布，不失一般性可以假设其服从正态分布。教学不仅要提高班级的平均水平，还要考虑怎么减少标准差，使整个班级的知识分布更加合理且优秀。要实现这一教学目标，教师就需要针对不同的学生制定相应的教学计划。将学生分成两个小组，接受知识能力强的称为优秀学生，接受知识能力弱的称为一般学生。

（2）教师教学阶段。对于出色学生组，通过下面方式获取知识：

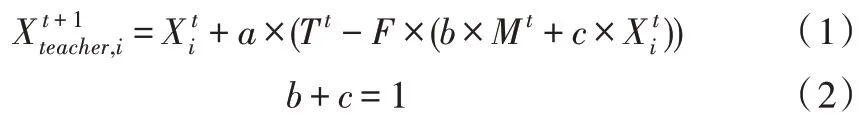
其中，t是当前的迭代次数，是i学生在t时刻时的知识，Tt是时刻t时教师所拥有的知识，Mt是在t时刻小组的平均水平知识，F是决定教师教学成果的教学因素，F值可以是1 或2，a,b,c都是［0，1］之间的随机数。

对于一般学生，获取知识的方式如下：

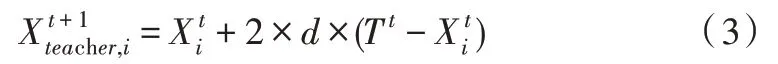
其中，d是［0，1］之间的随机数。

（3）学生学习阶段。学生学习阶段又可分成两个阶段，除开教师教学时间，学生可以在课余时间通过自学以及与其他优秀同学交流来获取知识，这一过程用下式来概括：

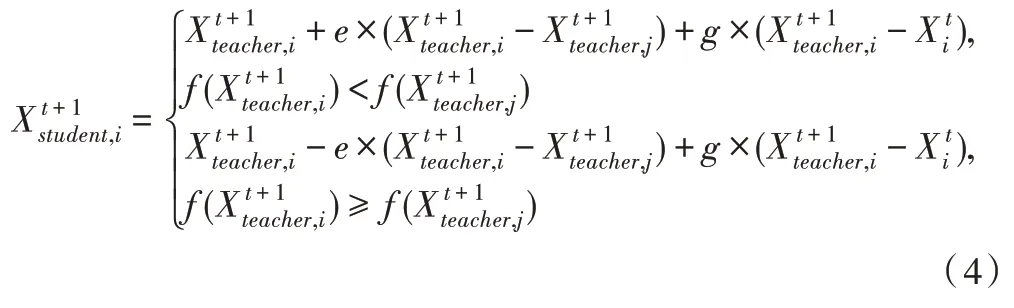
其中,e和g是［0，1］之间的随机数表示在t时刻时学生j在学习阶段学到的知识，学生j∈{1,2,…,i-1,i+1,…,N}是随机的。向其他学生交流学习和自学阶段学习分别是式（4）中的第2 项和第3 项。

（4）教师分配阶段。为保证算法的收敛速度，优秀学生组和一般学生组共用一位教师，而对教师的选择则受到灰狼优化算法（Grey Wolf Optimizer，GWO）中保留3 个最优的思想影响。具体的教师分配可根据下式选择：

GTOA 算法步骤如下：①初始化相关参数，随机产生含有N 个个体的学生种群；②计算个体的适应度值，选出最优解，并且更新函数迭代次数；③判断是否达到最大迭代次数，达到了即终止循环并输出最优解，否则跳转至第④步；④拿到3 个最优解，根据公式（5）选出教师；⑤基于个体的适应度值大小分组，将适应度值大的一半个体组成优秀学生组，将适应度值小的另一半个体组成一般学生组，两组学生共用一位教师；⑥对于优秀学生组根据式（1）、式（2）和式（4）更新种群；对于一般学生组，根据式（3）和式（4）分别执行教师教学阶段和学生学习阶段；⑦将两个新的种群合并组成一个新的种群，计算种群的适应度值，选取最优解，并且更新迭代次数，然后返回到第③步。

1.2 BP 神经网络

BP 神经网络是在人工神经网络基础上加入反向传播算法的多层前馈神经网络。BP 神经网络特点是信号正向传播，通过隐藏层和输出层的计算得到误差值，然后将误差一层一层地反向传播，更新网络中的权值和阈值，达到最优的期望值［19-20］。BP 神经网络（以一层隐含层为例）结构如图1 所示。

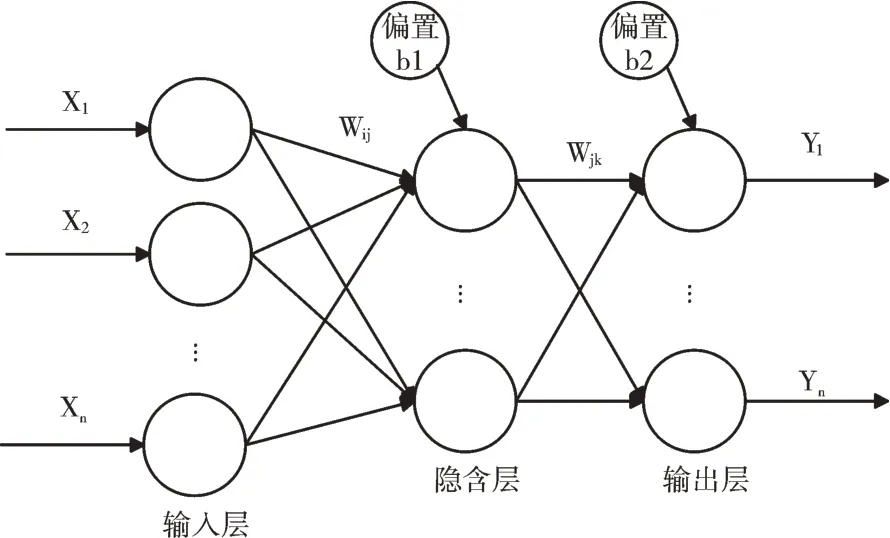
Fig.1 Three layer BP neural network structure图1 三层BP 神经网络结构

X1,…,Xn是网络的输入参数，Y1,…,Yn是网络的输出参数。初始化输入层个数n，隐藏层个数l，输出层个数m，输入参数经过输入层到达隐藏层公式如下：

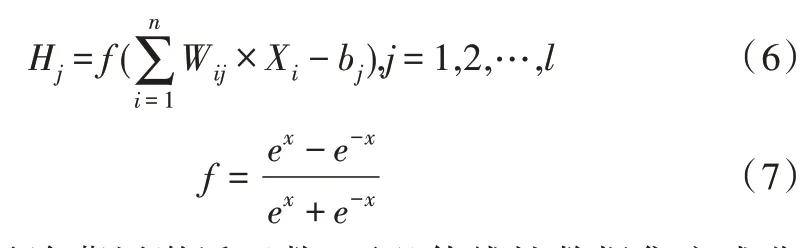
其中，f是隐藏层激活函数，可以使线性数据集变成非线性数据集。Wij和bj分别是输入层到隐藏层之间的权值和阈值。由隐藏层到输出层的计算公式如下：

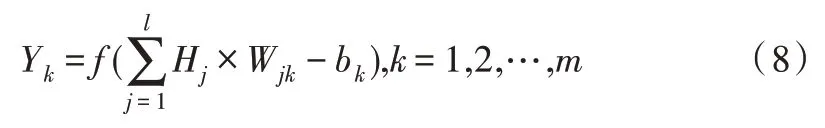
其中,f是输出层的激活函数，与隐藏层是同一个函数。Wjk和bk分别是隐藏层到输出层之间的权值和阈值。Yk是网络的预测输出值。得到输出值后计算误差，公式如下：

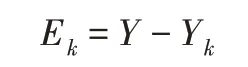
将误差反向传播到隐藏层，对隐藏层和输出层之间的权值和阈值进行更新，公式如下：

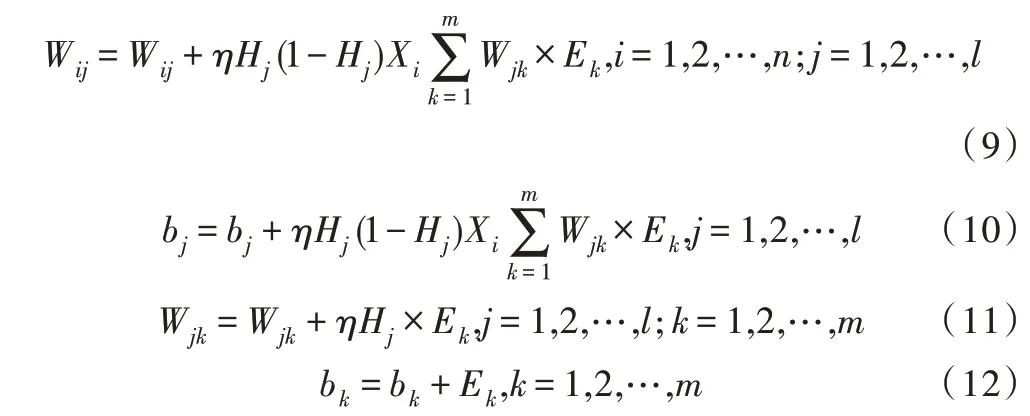
为使误差变小，再将误差传播至输入层，如此反复迭代训练，判断网络是否达到最大迭代次数或者达到最小误差条件。若没有结束，则继续使用更新后的权值与阈值进入网络循环，直至满足网络结束条件。

1.3 分组模式模型（GTOA-BP）

文献［18］提出的GTOA 算法在约束工程设计优化问题的广义求解方法中有着很好的结果，比如焊接梁设计问题、管柱设计问题、压力容器设计问题以及减速机设计问题，GTOA 优秀的全局搜索能力能使BP 神经网络中的性能函数实现快速收敛，得到GTOA-BP 中的最优权值与阈值，从而减少神经网络训练过程中产生的误差，提高预测精度。GTOA 算法由学生个体组成的种群与网络中的权值相对应，适应度函数是网络训练常用的性能函数均方误差（MSE）。模型具体步骤如下：

（1）对数据中农作物按照类型进行编号，然后将数据中样本的经度、纬度、海拔以及农作物编号4 个特征值作为神经网络输入参数，以重金属As（mg/kg）含量作为输出参数，对输入参数和输出参数最大、最小作归一化处理。

（2）确定BP 神经网络中隐藏层个数、激活函数、学习率、性能函数、网络训练次数以及GTOA 算法中种群大小和教学因素参数。

（3）初始化由权值与阈值个体组成的种群：

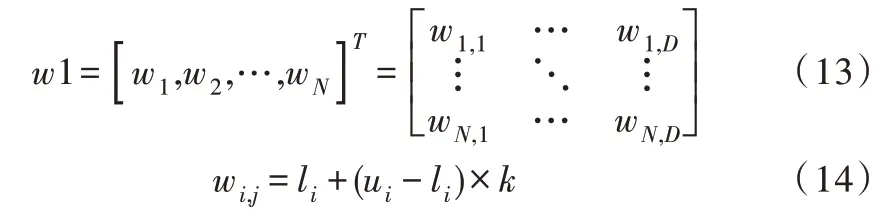
其中,N是生成种群大小，D是输入层个数，即维度，u和l分别是权值和阈值的上下界，k是［0，1］之间的随机数。

（4）计算种群适应度值，按照适应度值大小将种群分成优秀种群和一般种群。

（5）从分组的种群中按式（5）的种群选取教师。

（6）更新种群位置。优秀学生通过式（1）、式（2）、式（4），一般学生通过式（3）、式（4）完成教师教学阶段和学生学习阶段更新种群。

（7）重复步骤（4）-（6）直到满足结束条件，得到最优的权值和阈值。

具体流程如图2 所示。

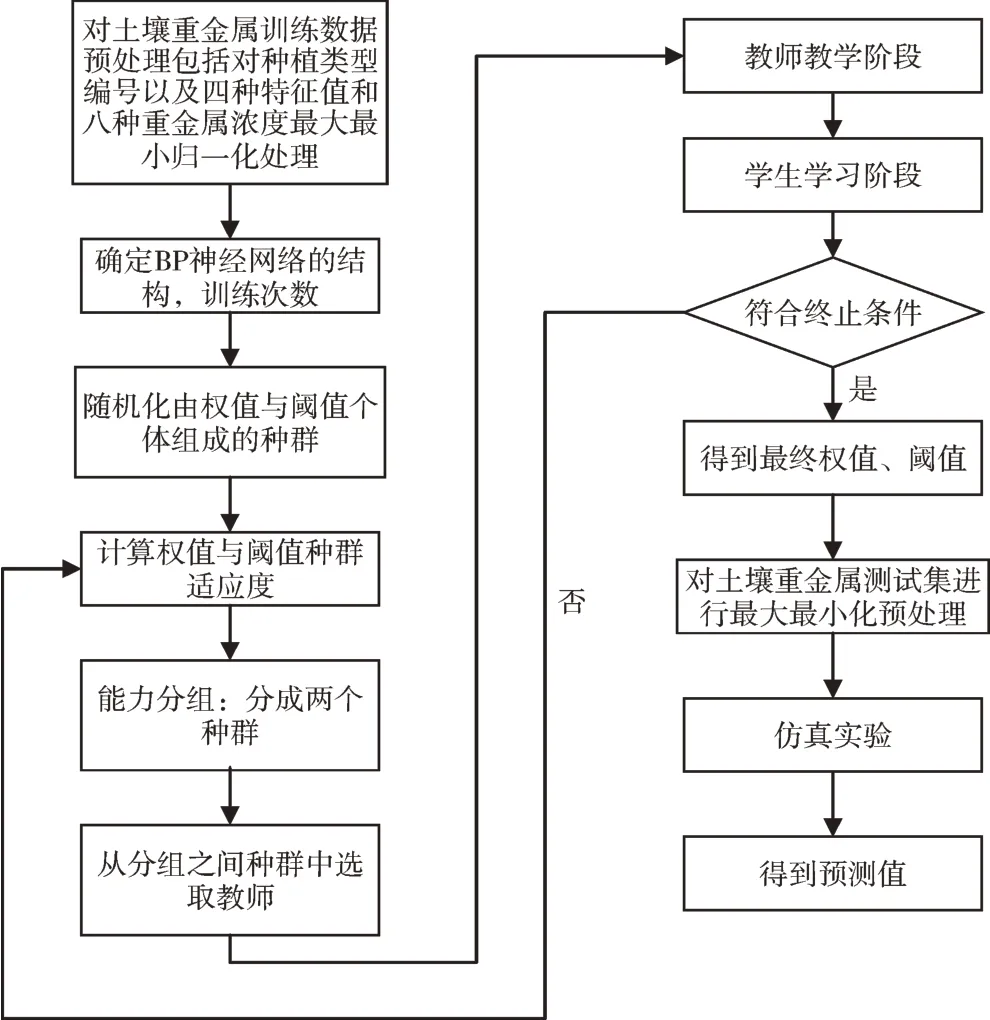
Fig.2 GTOA-BP model flow图2 GTOA-BP 模型流程

2 实验与结果分析

2.1 数据来源

本实验数据来自武汉市农科院环安所。依据《土壤环境监测技术规范》（HJ/T166-2004）和《土壤环境质量农业农用地土壤环境污染管控》（GB15618-2018）的要求，对武汉市6 个新城区的周边土壤中8 种重金属进行检测，包括砷（As）、铜（Cd）、铬（Cr）、铜（Cu）、镍（Ni）、铅（Pb）、锌（Zn）和汞（Hg），通过GPS 定位仪得到采样点的经度、纬度和海拔，记录了1161 个采样点的种植物类型。本研究的所有实验均在处理器为2.4 GHz 的四核Intel Core i5 以及操作系统为Windows 的电脑上进行，编程语言为Python，编程软件为PyCharm 2019 专业版。将数据中的农作物按照类型进行编号，把经度、纬度和高度的特征值作为模型输入参数，将8 种元素中的As 含量（mg/kg）作为实验模型输出参数，采用数据集中的500 组数据作为训练集，30 组数据作为测试集。

对数据进行预处理公式如下：

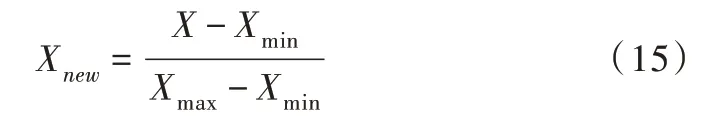
其中，X是原始数据，Xmax和Xmin分别是原始数据中的最大值和最小值。

2.2 实验结果分析

为了检验预测模型可行性，将GTOA-BP 模型分别与BP 神经网络模型和径向基神经网络模型（Radial Basis Function Neyral Network，RBFNN）进行对比，实验中BP 模型和RBF 模型迭代次数为600，激活函数采用tanh 函数，隐藏层节点数为8，学习率为0.02。GTOA-BP 预测模型种群大小为30，教学因素F为2，3 种模型训练下的As 含量真实值与预测值对比如图3-图5 所示。

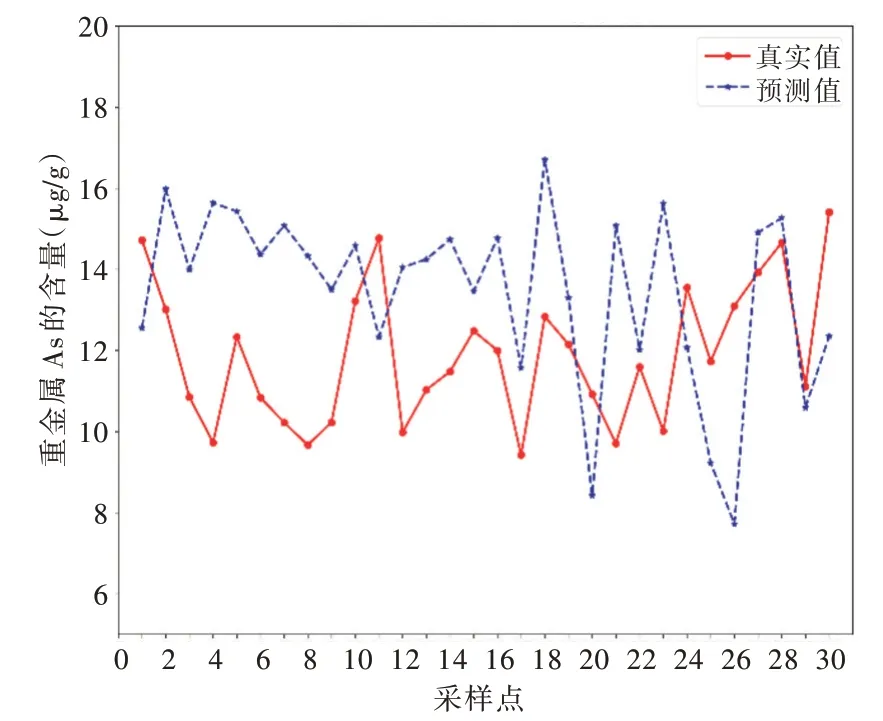
Fig.3 Comparison of As content in BP model图3 BP 模型As 含量对比

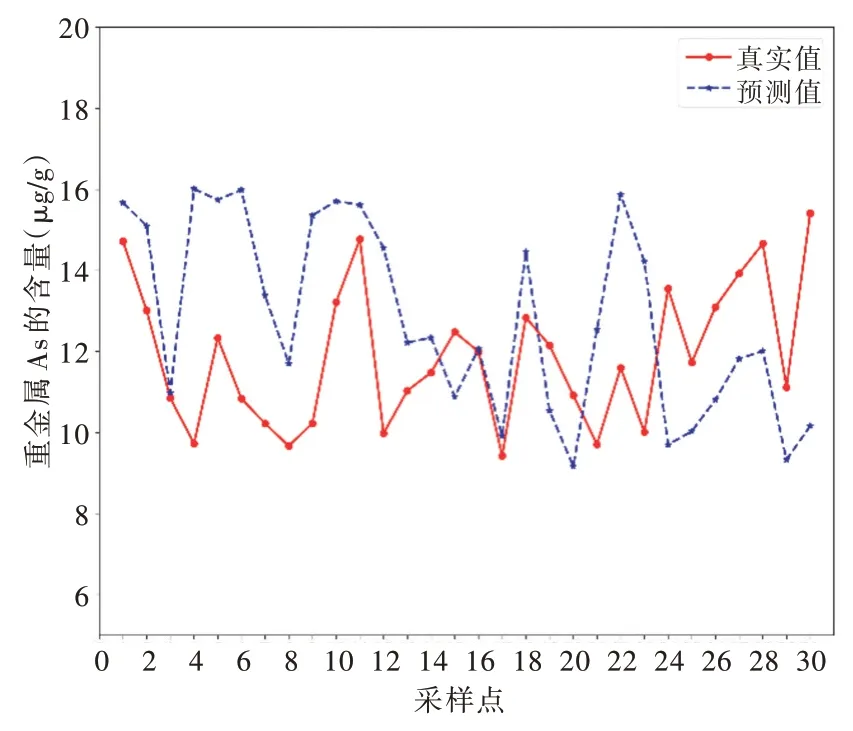
Fig.4 Comparison of As content in RBF model图4 RBF 模型As 含量对比

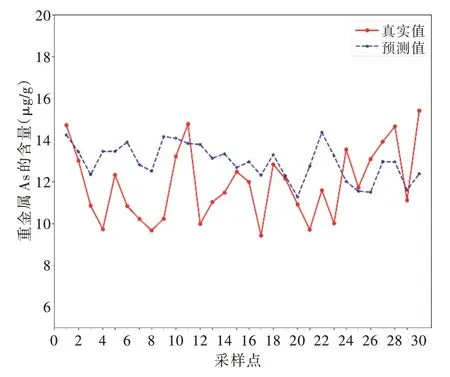
Fig.5 Comparison of As content in GTOA-BP model图5 GTOA-BP 模型As 含量对比

将预测得到的值与真实值作差值运算，然后得到差值与对应点的真实值比值大小，得到30 个测试点的分布，如表1 所示。

Table 1 Distribution of ratio of prediction points表1 预测点比值大小分布情况

平均绝对误差（MAE）、均方误差（MSE）、平均绝对百分比误差（MAPE）和对称平均绝对百分比误差（SMAPE）是4种可以评判预测效果的误差指标公式。计算公式如下：

结合图3、图4、图5 以及表1 和 表2 的数据可知，GTOA-BP 模型预测的数据相较于BP 模型和RBF 模型更加贴合真实数据，预测数据与真实数据差距较小。从表1 可以看出，GTOA-BP 模型得到的数值比其他两种模型可信度高，在比值小于10%时，GTOA-BP 有比其他两种模型一倍的预测点。由表2 可以看出，BPNN 模型和RBFNN 模型的4种误差指标数值均高于GTOA-BP 模型的误差指标，说明GTOA-BP 模型在3 种模型中预测效果最好。

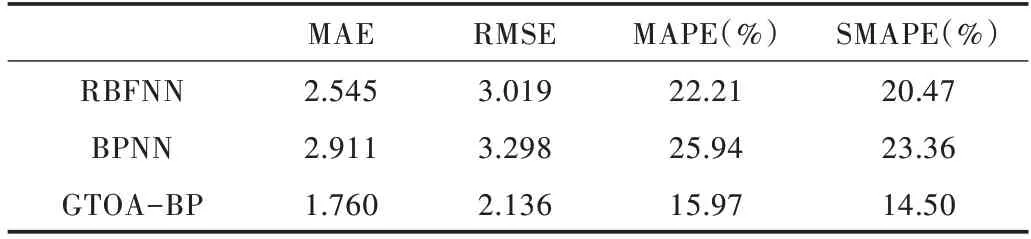
Table 2 Comparison of prediction errors表2 预测误差对比

3 结语

本文提出的GTOA-BP 预测模型通过GTOA 对BP 神经网络中的权值与阈值进行优化，相较于BPNN 和RBFNN 模型在土壤重金属含量预测效果方面有着更好的表现。通过分组模型对土壤中残留物进行预测，以此为基础对土壤重金属开展风险评估工作，为开展土地预防治理提供技术支撑。后续可以尝试将GTOA 运用到其他不同神经网络中，如日常生活中。但GTOA 算法还未运用于实际问题，算法还需进行优化以加快算法收敛速度。