基于GA-BPNN 的PM2.5 浓度预测模型

郑俊褒，华思洁

（浙江理工大学 信息学院，浙江杭州 310016）

0 引言

随着当前社会工业化水平的提升和自然灾害发生频率的增加，空气质量成为越来越值得重视的问题。PM2.5浓度是衡量空气质量的一项重要指标，它指环境空气中空气动力学当量直径小于等于2.5 微米的颗粒物，对人体健康危害极大，PM2.5 所吸附的重金属、苯并芘等致癌物、持久性有机污染物等，会经过呼吸系统进入人体，直接影响到肺，对人体造成重金属中毒、患癌几率上升、生殖生育危害等问题［1］。提前预测未来PM2.5 浓度可以为人们出行提供健康有效的信息［2］。

基于机器学习算法的PM2.5 浓度预测模型近年来发展迅速，张怡文等［3］利用PCA 的方法对数据进行降维，在提高预测准确率的同时，降低了时间复杂度，并将降维后的数据赋给BP 神经网络模型以完成预测；陈志文等［4］采用openstack 云计算组件，部署大数据平台以完善BP 神经网络，通过自我学习提高预测准确率；Luo 等［5］基于图像的方法，采用深度学习和机器学习扩展对PM2.5 的感知能力，构建卷积神经网络和梯度增强机，组成端到端模型进行预测；刘林波等［6］采用遗传算法优化后的BP 神经网络建立PM2.5浓度预测模型，验证其比BP 神经网络具有更好的精度。

作为传统经典算法，BP 神经网络在PM2.5 浓度预测领域也有着丰富的成果［7-9］，而由于其存在随机初始权值和阈值、隐含层神经元节点数选择具有主观性、易陷入局部最优等缺陷，模型精度还有较大提升空间［10-11］。神经网络的权值和阈值一般通过初始化为［-0.5，0.5］区间的随机数而确定，该初始化参数对网络训练影响很大，但是又无法准确获得［12］，对于相同的初始权重值和阈值，网络训练结果一样。本文引入遗传算法就是为了优化出最优的初始权值和阈值［13］，隐含层神经元节点数采用Kolmogorov 定理，设置为2n+1（n为输入层节点数），并在一层隐含层的结构基础上设置三层隐含层，提高特征学习能力，进一步提升PM2.5 浓度预测准确率［14-16］。

1 基于GA 的BPNN 优化算法

1.1 BP 神经网络

20 世纪80 年代，Rumelhart&McClelland 等学者提出了一种按照误差逆向传播算法训练的多层前馈神经网络，即为目前应用最广泛的BP 神经网络，BP 神经网络的基本思想是梯度下降法，利用梯度搜索技术，使得网络的实际输出值和期望输出值的误差均方差最小。

一个BP 神经网络模型通常由一个输入层、一个或多个隐含层、一个输出层组成，如何设计各层之间的权重值是构建BP 网络的重点。

近年来，BP 神经网络以其强大的非线性映射能力和泛化性、独特的适应性，在函数逼近、模式识别、分类问题、数据压缩等领域均取得了丰富的成果。但同时，它也存在收敛速度慢、易陷入局部最优、网络层数和神经元个数容易受主观影响等问题［17-18］。

1.2 算法流程

遗传算法是根据大自然中生物体进化规律而提出，是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。针对BP 神经网络易陷入局部最优的缺陷，本文利用遗传算法的全局搜索能力优化BP 网络的初始权重值和阈值，使优化后的预测模型能够更好地进行训练和测试。基于遗传算法优化BP 神经网络流程如图1 所示。

Fig.1 Algorithm process图1 算法流程

1.3 遗传算法实现

使用遗传算法优化BP 神经网络权值和阈值的主要步骤为种群初始化、适应度函数计算、选择、交叉重组、变异、子代重插入到父代得到新种群、代计数器增加、记录每代最优值。

（1）种群初始化。本文的网络结构是10-21-21-21-1，权值和阈值个数如表1 所示。

Table1 Number of weights and thresholds表1 权值、阈值个数

个体编码采用二进制编码，每个个体均为一个二进制串，由输入层与第一隐含层连接权值、第一隐含层阈值、第一隐含层与第二隐含层连接权值、第二隐含层阈值、第二隐含层与第三隐含层连接权值、第三隐含层阈值、第三隐含层与输出层连接权值、输出层阈值8 个部分组成。假定编码为10 位二进制数，则个体二进制编码长度为11 770。其中，1～2 100 位为输入层与第一隐含层的连接权值编码；2 101～2 310 位为第一隐含层阈值，依此类推。

（2）适应度函数。本文所用的适应度分配函数为：FitV=ranking（obj），obj 为目标函数的输出。为了使预测值与实际值的残差尽可能小，目标函数的输出设置为测试样本的预测值与实际值的误差矩阵的范数。

（3）选择、交叉重组、变异。其中，选择算子使用随机遍历抽样（sus），交叉算子使用单点交叉算子，变异是以一定概率的随机方法选出变异基因，将其二进制编码进行0-1交换。

2 模型构建与实验

2.1 数据预处理

2.1.1 数据缺失值及特征化处理

本文数据预处理包括缺失值处理、特征化处理、卡方检验确定影响因子以及归一化处理。

本次实验的数据来自中国环境监测总站的全国城市空气质量实时发布平台，以杭州市为例，选取2020 年5 月1日至2020 年6 月20 日、时间间隔为一小时的共1 223 组数据，数据集包括PM2.5、PM10、SO2、NO2、O3、CO 浓度，其中缺失2 组，以等间距牛顿插值法补全，如式（1）所示。

其中，h为节点间距，x1、x2分别为缺失值的前后两个数据。

天气相关数据来自www.k780.com 网站，它提供了包括温度、湿度、风向、风级以及天气状况在内的以小时为单位采集的数据，同样收集2020 年5 月1 日至2020 年6 月20 日之间的数据。

神经网络无法识别文本数据，因此将数据中的风向（东北、东、东南、南、西南、西、西北、北）分别用1-8 代替，天气状况（晴、多云、阴、雨）分别用1-4 代替。

2.1.2 卡方检验确定影响因子

为确定天气数据中哪些为PM2.5 浓度的影响因子，本文采用卡方检验方法得到这些数据。其中，温度、湿度、风级和天气状况会影响PM2.5 的浓度。以湿度为例，进行卡方检验具体步骤如下：

（1）H0假设湿度与PM2.5 浓度（单位：μg/m3）无关，平均湿度（采用四舍五入，单位：%单位湿度）与PM2.5 浓度的频数如表2 所示。

Table 2 Frequency relationship between average humidity and PM2.5 concentration表2 平均湿度与PM2.5 浓度的频数关系

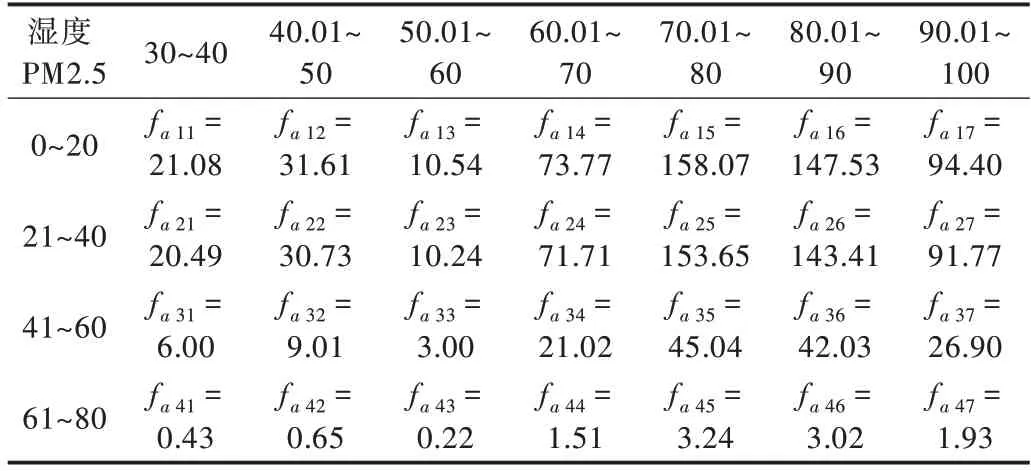
Table 3 Expected frequency of average humidity and PM2.5 concentration表3 平均湿度与PM2.5 浓度的期望频数

（3）确定自由度（7-1）*（4-1）=18，取显著性水平0.005，根据CHIINV（0.005，18）得到临界值P=37.2。

（4）因为x2>P，则拒绝原假设，即湿度与PM2.5浓度有关。

2.1.3 数据归一化处理

由于PM2.5 浓度的各影响因子数据范围不同，可能会影响神经网络的训练速度和表达能力，为提升模型效果，先对数据集进行归一化处理，本文采用max-min 数据归一化方法，将所有数据缩放到0-1 范围内。

其中，x为原始值，xmax、xmin分别为该变量的最大值和最小值，xn为归一化处理后的值。

2.2 模型构建

2.2.1 模型结构

在BP 神经网络模型建立过程中，输入、输出数据的选择会直接影响到模型性能。本文预测杭州市PM2.5 浓度变化，输入数据层为前一时刻的PM2.5、PM10、SO2、NO2、O3、CO 浓度，以及温度、湿度、风级和天气状况，输出层为后一时刻的PM2.5 浓度。训练数据集为前1 023 组，测试数据集为后200 组。

考虑到PM2.5 浓度预测是一个涉及时间序列的较为复杂的非线性函数，一层隐含层的拟合效果不一定能很好地达到预期效果，因此本文神经网络模型的隐含层层数设置为三层，模型结构如图2 所示。

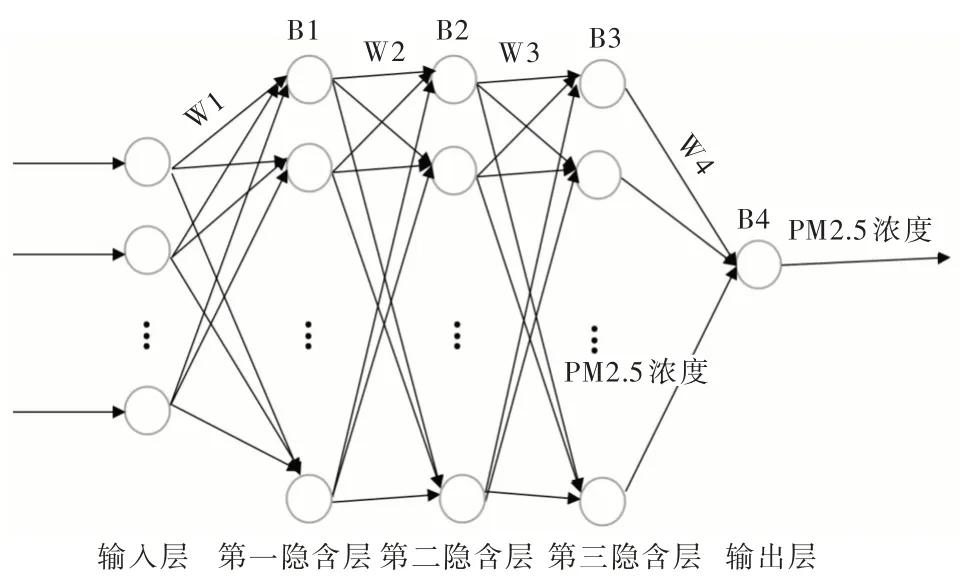
Fig.2 Neural network topology图2 神经网络拓扑结构

其中，wi为各层之间权重值，Bi为各隐含层与输出层的阈值。

为了将多个线性输入转换为非线性关系，需要在隐含层与输出层的输入与输出之间添加激励函数，激励函数取双曲正切函数：

训练函数取L-M 优化算法，即trainlm 函数，该算法对于中等规模的BP 神经网络有着最快的收敛速度。

2.2.2 模型建立

为验证GA-BP 神经网络模型在PM2.5 浓度预测问题上的可操作性和有效性，在配置为64 位、内存为8GB 的Mac OS X操作系统与MATLABR2017b平台上进行仿真实验。

本文将遗传算法与BP 神经网络结合，构成GA-BPNN模型，用遗传算法概率化的寻优方法，自适应地调整搜索方向，确定输入层与第一隐含层、各隐含层之间、第三隐含层与输出层的最优权重值，以及各隐含层与输出层的最优阈值，使得原BP 神经网络模型在预测效果上得到提升。实验相关参数如表4、表5 所示。

Table 4 Genetic algorithm parameter setting表4 遗传算法参数设置

Table 5 GA-BP model parameter setting表5 GA-BP 模型参数设置

3 实验结果及分析

3.1 评价指标

本文采用的模型预测精度评价指标主要包括均方根误差（RMSE）、平均绝对误差（MAE）、一致性指数（IA）。均方根误差和平均绝对误差是衡量预测值与实际值之间的偏差，其值越小越好，一致性指数则是预测值和实际值趋势变化的体现，越接近于1 说明变化的一致性越高。

其中，N为预测样本个数，T_sim为模型预测值，T_test为样本实际值，为样本实际值的平均值。

3.2 GA-BPNN 模型与比较模型预测结果分析

为验证本文算法的可行性，使用训练数据集分别训练随机权值和阈值的传统BPNN 模型、传统LSTM 模型、基于GA 优化后的权值和阈值的BPNN 一层隐含层模型和三层隐含层模型，预测结果如图3—图6 所示，4 种模型的相对误差比较如图7 所示。

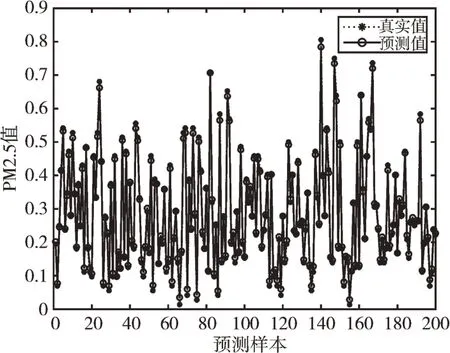
Fig.3 BPNN prediction effect图3 BPNN 预测效果

Fig.4 Traditional LSTM model prediction effect图4 传统LSTM 模型预测效果

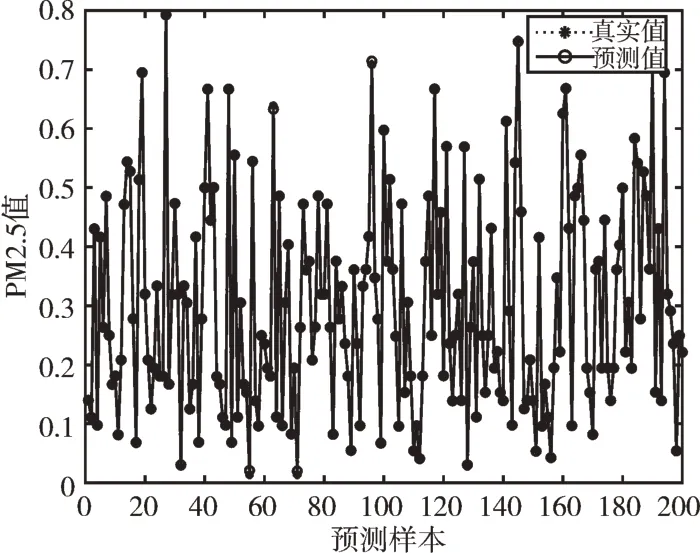
Fig.5 Prediction effect of one hidden layer of GA-BPNN图5 GA-BPNN 一层隐含层预测效果

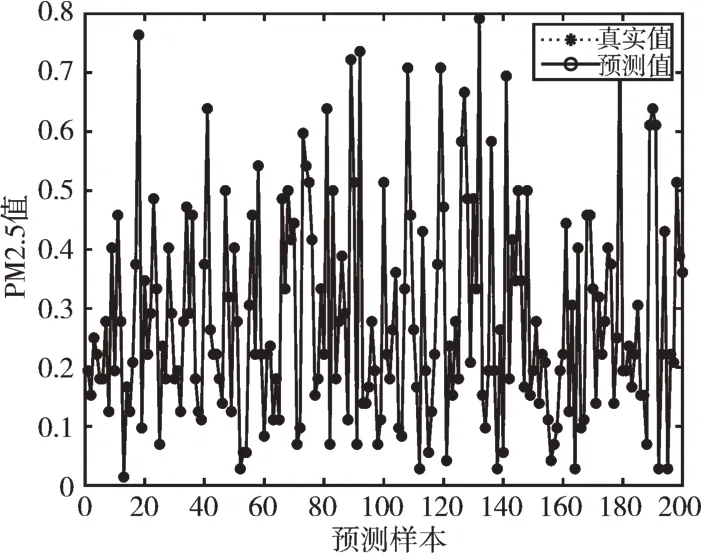
Fig.6 Prediction effect of three hidden layers of GA-BPNN图6 BPNN 三层隐含层预测效果

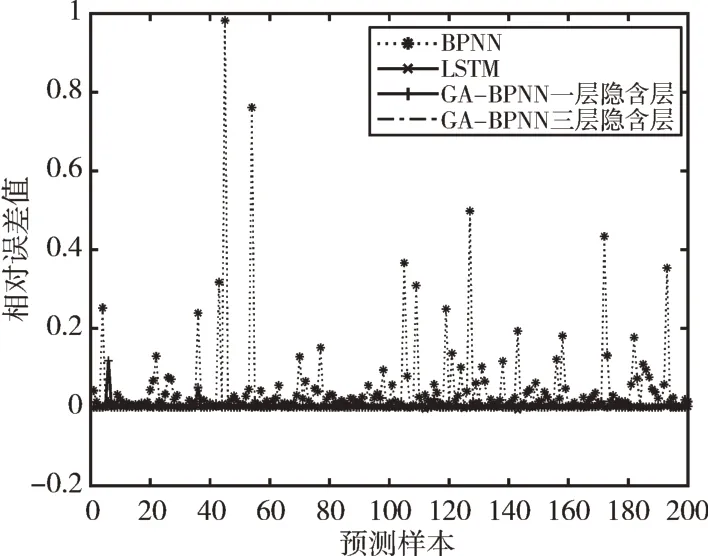
Fig.7 Comparison of the relative errors of the four models图7 4 种模型相对误差比较

由图3—图6 可以看出，GA-BPNN 模型的预测曲线比传统BPNN 模型更为贴合，而三层隐含层的效果比一层隐含层拟合度更高，预测精度更好；由图7 可以看出，GABPNN 模型的相对误差值相对BPNN 模型和LSTM 模型明显下降，说明预测效果得到提升。4 种模型的预测评价指标如表6 所示。

Table 6 Model evaluation index comparison表6 模型评价指标比较

可以看出，相较于传统BPNN 模型和传统LSTM 模型，本文GA-BPNN 模型相对于传统BPNN 在误差上降低了较大幅度，拟合度也得到了16.4%的提升，使用GA-BPNN 算法在运行时间上虽稍有增加，但仍在合理范围内，说明GA-BPNN 模型针对PM2.5 浓度预测准确性较高，同时有较快的收敛速度及较好的稳定性，是一种应用前景良好的预测模型。

4 结语

PM2.5 浓度的变化会受到土壤扬尘、植物花粉、细菌、自然灾害等自然源和工业燃料燃烧、交通工具尾气排放、不完全燃烧的烟草产品等人为源因素的影响，具有很强的实时性与复杂的非线性。本文为解决BPNN 存在的易陷入局部最优的问题，将具有良好全局寻优能力的遗传算法与强大的非线性映射能力的BPNN 相结合，提出了基于GABPNN 模型的PM2.5 浓度预测模型，用得到的最优权值及阈值进行训练，将优化后的模型用于预测，并与传统BPNN 模型作比较。实验结果表明，本文算法在预测精度上有所提升，均方根误差和平均绝对误差降低，拟合结果更优，可以为PM2.5 浓度提供更完善的预测信息。在遗传算法训练过程中，迭代次数相对较高是目前存在的问题，如何提高算法收敛速度是下一步研究方向。