基于强化学习的随机振动主动控制策略

周嘉明，董龙雷，孟 超，孙海亮

(1.西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室，西安 710049；2.北京宇航系统工程研究所，北京 100076)

振动控制方法主要有3种：被动控制、主动控制和半主动控制。被动控制不需要外界施加能量，只需一些无源的弹性元件或阻尼元件，如金属弹簧、橡胶阻尼垫等。被动控制的优势在于结构简单、可靠性高，但是对低频振动和宽频随机振动的抑制效果较差。随着控制理论、作动传感技术和计算机科学的不断发展，振动主动控制技术已经在航空航天、车辆和土木工程等领域取得了诸多成功的应用[1-4]。振动主动控制系统主要由作动器、传感器、控制策略和被控对象组成。与被动控制相比，主动控制具有较强的灵活性和环境适应性，但是用于主动控制的作动器通常价格昂贵、能耗大、可控力较小，如压电作动器[5]、音圈电机等，因此学者们提出了振动半主动控制技术。半主动控制是一种物理参数控制技术，主要通过调节系统的刚度或阻尼来实现，比如利用形状记忆合金或磁流变弹性体调节刚度[6-7]、利用电/磁流变液调节阻尼[8]。

影响振动主动/半主动控制效果的关键因素之一是控制策略。比例积分微分(proportional-integral-derivative，PID)控制是一种使用最为广泛的控制策略，目前已经在很多系统上取得了成熟的应用，比如离散系统[9]、连续体系系统[10-11]等。PID控制很难处理高维反馈信号和控制信号，这在一定程度上限制了它的应用。随着高维控制问题的出现，基于状态空间的现代控制理论得到了快速地发展，这些方法也被引入到振动主动控制领域，其中最常见的算法包括线性二次调节器(linear quadratic regulator,LQR)[12-13]和线性二次高斯控制(linear quadratic gaussian,LQG)[14]。控制器设计的前提往往需要建立被控系统精确的数学模型，但是实际系统往往存在不确定性、非线性等复杂特征，这使得数学模型的精度较差，甚至无法得到数学模型。为此，学者们提出了一些智能控制策略，主要包括自适应控制[15-18]、模糊控制[19-21]以及神经网络控制[22-25]等。

现有智能控制策略的设计仍然依赖专家经验的参与，且需花费大量的时间。强化学习(reinforcement learning,RL)是与有监督学习和无监督学习并列的第三种机器学习范式，旨在通过智能体和环境的互动来最大化累积奖励的期望，其中智能体指强化学习算法；环境指被控对象的数学模型；奖励指智能体采取动作(控制信号)后获得的回报，这是强化学习算法能够学习的关键。强化学习的核心是强化学习算法，常见的算法有Q-Learning、DQN[26]、REINFORCE、A3C[27]以及深度确定性策略梯度(deep deterministic policy gradient，DDPG)等。DDPG是一种基于确定性策略梯度的Actor-Critic算法，优势在于可以适用于连续控制问题，将作为本文设计振动控制器的强化学习算法。

挑战现有控制策略的两大因素主要是被动对象参数的不确定性和非线性。为此，本文提出了一种基于强化学习的随机振动主动控制策略，这种由强化学习算法设计的控制器称为RL-NN(neural network controller designed by reinforcement learning)控制器。RL-NN控制器是基于数据驱动设计完成的，不依赖系统精确数学模型的参数和大量的领域知识，在一定概率分布范围内产生大量数据供强化学习算法学习即可；另外，神经网络具有强大的非线性表示能力，可以很好地近似被控对象中的非线性动力学行为。最后，通过两个数值算例对RL-NN控制器的性能进行验证：①考虑不确定性的单自由度系统主动控制；②考虑不确定性和非线性的车辆1/4磁流变悬架系统半主动控制。

1 RL-NN控制器设计方法

1.1 RL-NN控制框架

RL-NN控制器是一个多层神经网络，将传感器测量的反馈信号(如位移、速度、加速度等)直接输入给神经网络，经过正向运算后将输出的控制信号(如电压、电流等)直接施加在作动器上，从而实现系统闭环振动主动/半主动控制。RL-NN控制框架示意图，如图1所示。

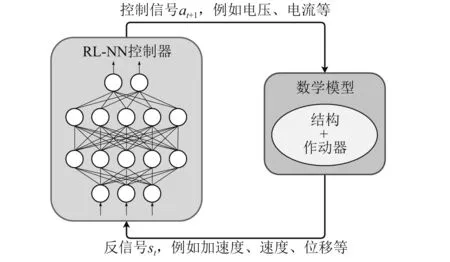
图1 RL-NN控制框架示意图Fig.1 Schematic diagram of the RL-NN control framework

不同于一些自适应控制算法，RL-NN控制器的参数是固定的，在控制过程中不需要实时更新；其次，该控制器的模型规模小，方便硬件部署，可以非常快速地计算出反馈信号，一定程度上缓解了控制器的时滞性。另外，RL-NN控制器允许高维输入和高维输出，可以很容易地解决多输入多输出控制问题。

RL-NN控制器的参数(神经网络各层的权重和偏置)通过强化学习算法与数据自主交互学习后确定，该过程不依赖于振动控制领域知识。

1.2 强化学习算法

DDPG是一种基于Actor-Critic的强化学习算法，如图2所示。DDPG算法中包含4个神经网络，分别是策略网络、目标策略网络、价值网络和目标价值网络。策略网络和价值网络与其对应目标网络的架构是完全相同的，仅存在网络参数的差异性。策略网络和价值网络会不断将自身参数通过一种软更新的方式拷贝给各自的目标网络，其目的主要是为了减少目标计算与当前值的相关性，从而使学习过程更加稳定、易于收敛。

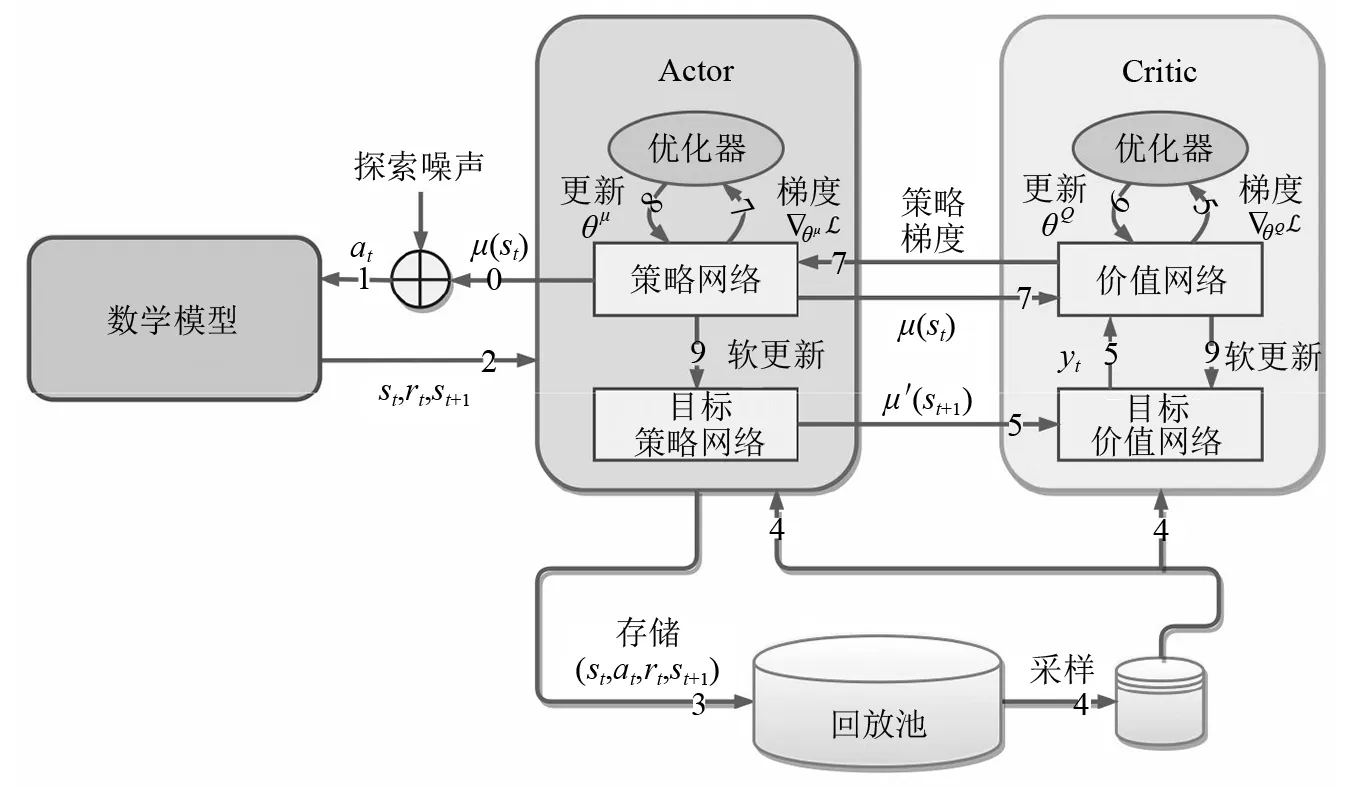
图2 DDPG算法示意图Fig.2 Schematic diagram of DDPG algorithm

由于采用软更新方法，DDPG算法只需要计算出策略网络和价值网络的梯度，然后通过反向传播算法更新网络的参数即可。策略网络和价值网络损失函数的表达式为

yi=ri+γQ′(si+1,μ′(si+1|θu′)|θQ′)

(1)

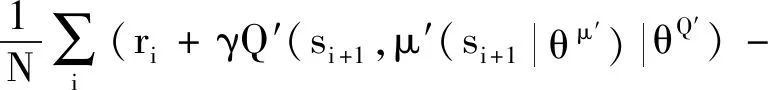
Q(si,ai|θQ))2

(2)

(3)

式中：Lμ和LQ为策略网络和价值网络的损失函数；θμ，θμ′，θQ和θQ′为策略网络、目标策略网络、价值网络和目标价值网络的参数；μ(·)，μ′(·)，Q(·)和Q′(·)为策略网络、目标策略网络、价值网络和目标价值网络的前向计算函数；s，a和r分别为反馈信号、控制信号和回报信号；γ为回报信号的衰减系数；N为学习样本数目，i=1,2,…,N。

目标网络参数的更新采用

θQ′←τθQ+(1-τ)θQ′,

θμ′←τθμ+(1-τ)θμ′

(4)

式中，τ为目标网络参数的更新系数，一般τ<<1。

DDPG算法采用了经验回放机制，即通过引入回放池，将计算得到的元组数据(si,ai,ri,si+1)不断储存到回放池中，然后通过随机采样的方式选取样本供算法学习，经验回放机制可以有效地降低学习样本的时序相关性，提升DDPG算法的学习能力。对于反馈信号中不同物理量量级存在差异的问题，比如加速度、速度和位移信号一般存在数量级的差异，本文采用批归一化的方式进行处理，这样可以使神经网络很好地处理不同数值范围的输入，同时缓解神经网络中间层输出“漂移”、梯度发散等问题[28]。在训练的过程中，对策略网络的输出添加一定的高斯噪声，这样可以使算法探索潜在的更优策略，噪声的量级随着训练逐渐递减，从而保证“探索”和“开发”之间的平衡。

1.3 RL-NN控制器设计流程

本文设计RL-NN控制器的步骤主要包括以下3个部分。

1.3.1 建立被控对象的数学模型

建立可以反映被控系统动力学特性的数学模型，模型的参数满足特定的概率分布，从而体现被控系统的不确定性。建立数学模型的目的主要有两方面：一是计算控制信号at参与后的反馈信号st+1；二是计算控制信号at参与后的回报信号rt。本文的回报信号均采用位移信号，即强化学习的目标是最小化控制位置处的振动位移。微分方程的数值解均采用四阶龙格-库塔法获得。

1.3.2 控制策略的自主学习

DDPG算法与被动对象的数学模型进行数据交互，如图2所示。通过1.2节中的式(1)～式(4)对4个网络的参数进行更新，从而实现控制策略的自主学习。本文使用的策略网络和价值网络均包括两个隐含层，每层有32个神经元，隐含层的激活函数均采用ReLU。策略网络输出层的激活函数采用tanh，而价值网络输出层采用线性激活函数。使用ADAM优化器更新策略网络和价值网络的参数，学习率分别设置为1-5和1-4。其他参数设置为：回放池的存储空间为1×105，随机采样个数为N=256，回报信号的衰减系数为γ=0.99，目标网络参数的更新系数为τ=0.001。

1.3.3 获取RL-NN控制器

记录并观察回报信号的变化情况，当回报信号达到收敛平稳趋势时终止学习，保存策略网络的架构和参数，最终得到的策略神经网络便是强化学习算法设计的RL-NN控制器。将RL-NN控制器部署在软件或硬件平台上，将传感器采集到的反馈信号作为神经网络的输入，通过神经网络的正向计算后输出控制信号，从而完成系统振动主动/半主动控制的闭环过程。

2 单自由度系统主动控制

2.1 问题描述

用于振动主动控制的单自由度系统的动力学模型，如图3所示，其动力学控制方程为

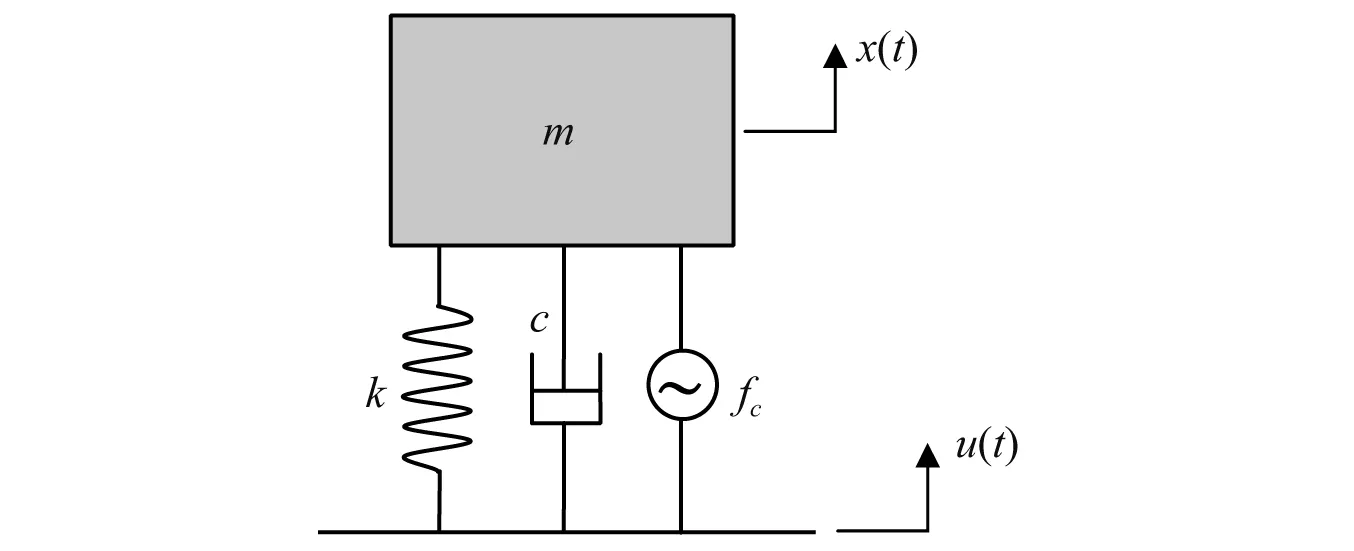
图3 单自由度系统的动力学模型Fig.3 Dynamic model of single-degree-of-freedom system

(5)

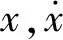
主要考虑m，c，k参数的不确定性，假设这3个参数都满足均匀分布，不确定性范围设置为20%，即m∈[0.8m0,1.2m0]，c∈[0.8c0,1.2c0]，k∈[0.8k0,1.2k0]，其中m0=1 kg，c0=3 Ns/m，k0=100 N/m。m，c，k参数的不确定性空间，如图4所示。将大量具有不同参数的单自由度系统计算得到的数据提供给强化学习算法，让强化学习算法学习隐藏在数据中的不确定性，从而使得RL-NN控制器可以很好地适应系统的不确定性。

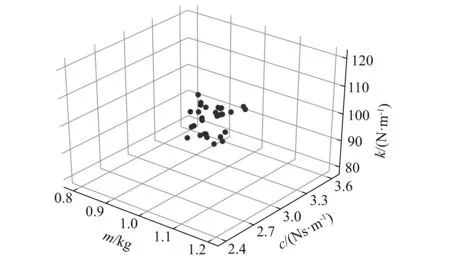
图4 单自由度系统参数不确定性空间Fig.4 Parameter-uncertainty space of single-degree-of-freedom system

2.2 控制结果

单自由度系统的位移控制曲线和控制电压，如图5所示。通过1 000次Monte Carlo模拟来验证RL-NN控制器的性能，位移均方根(root mean square，RMS)值的计算结果，如表1所示。可以看出在系统参数具有20%的不确定性时，RL-NN控制器可以实现97.55%的控制效果，且标准差仅有0.001 8%，这表明强化学习算法学习到的主动控制策略可以很好地适应系统参数的不确定性，且控制性能优异、稳定性高。

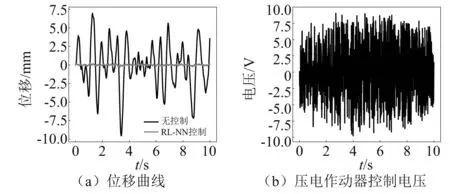
图5 单自由度系统振动主动控制结果(m=0.8 kg,c=2.6 Ns/m,k=117.6 N/m)Fig.5 Active vibration control results of the single-degree-of-freedom system(m=0.8 kg,c=2.6 Ns/m,k=117.6 N/m)

神经网络在进行数据外推时会出现性能恶化的问题，即泛化能力下降。为此，通过1 000次Monte Carlo模拟来验证系统具有30%，40%，50%以及60%不确定性时RL-NN控制器的性能，计算结果如表1所示。可以看出随着不确定性的增加，RL-NN控制器的性能出现略微的下降。在60%不确定性情况下，RL-NN控制器可以实现96.59%的控制效果，方差仅有0.035%，相对于20%的不确定性，控制效果下降的幅度不足1%。结果表明在系统参数不确定性估计保守的条件下，RL-NN控制器仍具有良好的泛化性能，控制效果优异且稳定。

表1 单自由度系统位移控制结果Tab.1 Displacement control result of single-degree-of-freedom system

3 车辆1/4悬架半主动控制

3.1 问题描述

用于振动半主动控制的车辆1/4悬架系统的动力学模型，如图6所示，其动力学控制方程的表达式为

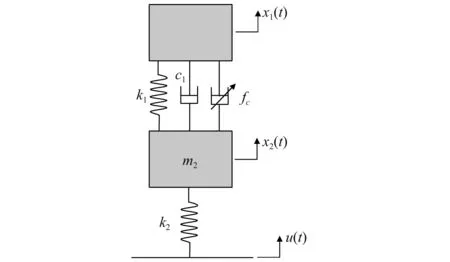
图6 车辆1/4悬架系统的动力学模型Fig.6 Dynamics model of quarter-suspension system of vehicle

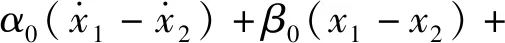
(6)

式中：m1和m2分别为簧载质量和非簧载质量；k1和k2分别为弹簧刚度和轮胎刚度；c1为不可控阻尼系数；fc为磁流变阻尼器的可控阻尼力；α0,β0,γ,α1和β1为描述控制电流与可控阻尼力关系的参数；i为控制电流，i∈[0,3 A]。本文采用的磁流变阻尼器模型和相关动力学参数均引用文献[29]。本算例中,半主动元件磁流变阻尼器具有典型的强非线性特性，这对振动半主动控制器的设计带来了很大的困难。

3.2 控制结果

车辆1/4悬架系统簧载质量m1的位移主动控制曲线和控制电流，如图7所示。为了更好地表明本文所提方法的优异性，引入sky-hook控制策略作为对比。sky-hook控制策略是车辆悬架半主动控制领域应用最为广泛的控制策略，可以描述为[30]

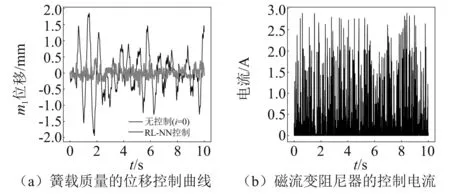
图7 车辆1/4悬架系统振动半主动控制结果Fig.7 Semi-active vibration control results of the vehicle 1/4 suspension system

(7)

考虑20%不确定性，对比被动控制(磁流变阻尼器的控制电流为0)和RL-NN控制下簧载质量块m1和非簧载质量块m2的位移RMS值，结果如表2所示。对于簧载质量，sky-hook的控制效果为46.80%，标准差为1.55%，而RL-NN控制器可以实现74.39%的控制效果，且标准差仅有0.24%，结果表明本文所提的方法比sky-hook的控制效果至少高出25%，且控制效果更加稳定。对于非簧载质量，sky-hook的控制效果比RL-NN控制高出约1%，这主要是因为RL-NN控制器在学习过程中回报信号未考虑非簧载质量造成的，后续仍有一定的提升空间。

表2 车辆1/4悬架系统位移控制结果Tab.2 Displacement control result of quarter-suspension system

sky-hook是一种模糊控制策略，可以很好地适应系统的不确定性和非线性，是人类专家多年来在理解物理模型的基础上结合反复迭代经验总结出的控制策略。RL-NN控制器仅需要在普通计算平台上学习数小时便可以超越人类专家水平，这在一定程度上体现了通过强化学习来设计控制策略的潜力，为复杂系统振动主动/半主动控制器的设计提供新的实现途径。

4 结 论

本文提出了一种基于强化学习的振动主动控制策略，即利用强化学习算法DDPG设计多层神经网络控制器。通过单自由度系统振动主动控制计算表明，RL-NN控制器可以适应系统参数的不确定性，其控制效果可以达到97%，且稳定性优异；另外，RL-NN控制器具有良好的泛化性能，在系统参数不确定性达到60%时控制效果下降不足1%。通过车辆1/4悬架振动半主动控制计算表明，RL-NN控制器可以适应系统参数的不确定性和非线性，其控制效果达到74%，比sky-hook高出至少25%，且控制稳定性更加突出。基于强化学习方法的控制策略可以大幅度缩短控制器设计的时间，仅需要在普通计算平台上学习数小时便可以达到甚至超越人类专家水平，这为不确定性和非线性系统的振动主动/半主动控制器的设计提供了新的实现途径。