高延性混凝土加固震损混凝土短柱轴压性能试验及承载能力研究

寇佳亮，李 豹，徐 炎，景国强，周 恒

(1.西安理工大学 土木建筑工程学院，西安 710048；2.西安理工大学 省部共建西北旱区生态水利国家重点实验室，西安 710048；3.中国电建集团 西北勘测设计研究院有限公司，西安 710065)

已建成的混凝土结构因自然灾害、结构老化、钢筋锈蚀等因素导致结构承载力不足、变形和裂缝过大，影响建筑结构的使用功能与安全要求。拆除受损结构势必会造成不必要的损失与浪费。因此，对受损混凝土结构进行加固、提高其使用年限就显得尤为有意义。

目前对于钢筋混凝土结构的加固方法[1]常用的有增大截面法、置换混凝土加固法、粘贴纤维复合材加固法等，但是由于并没有从本质上改变混凝土脆性易开裂的特性以及施工、造价等问题，受损钢筋混凝土结构的加固与修复效果并不是十分理想。

Li等[2]提出了一种新材料:工程水泥基复合材料(engineered cementitious composite,ECC)，它是以微观力学和断裂力学为原理，对复合材料进行优化设计，在各种荷载作用下表现出良好的高延展性，具有假应变硬化特征和多裂缝开展的特性[3-5]。基于ECC材料良好的裂缝宽度控制能力，结合陕西地方材料，课题组配制出了高延性混凝土(high ductile concrete，HDC)。在掺加定量纤维(体积分数≤2%)下，HDC仍具有超高的延展性和多裂缝开展的的特性，并且与混凝土具有良好的黏结能力。

利用HDC良好的裂缝宽度控制能力和黏结能力，用于加固受损混凝土结构显得十分可行。目前国内已有很多学者研究了ECC加固，邓明科等[6]采用ECC面层加固受损的砖砌体墙并进行了抗震性能研究，结果表明ECC面层的加固能够很好约束砖砌墙，提高墙体的稳定性，同时大幅度改善了砖砌墙脆性破坏的特性，提高其变形能力。张远淼等[7]采用ECC修复了震损剪力墙并进行了拟静力试验研究，研究结果表明采用ECC修复的剪力墙，其承载力基本得到恢复，墙体耗能提高，延性也有很大程度提高，剪力墙由脆性破坏转为延性破坏。徐世烺等[8]采用RUHTCC材料加固梁的受弯试验，结果表明RUHTCC梁具有很高的承载力与变形能力，延性与多裂缝控制能力也较普通混凝土高很多。李易越[9]通过ECC钢筋网加固了钢筋混凝土(reinforced concrete，RC)方柱，轴压试验表明，一次受力下的加固柱比RC方柱具有更高的峰值应变，峰值荷载提高幅度可达71%，对柱身裂缝开展的抑制作用也非常明显。课题组前期通过13根HDC加固受损混凝土短柱的轴压试验[10]，研究了HDC对受损混凝土的承载能力和变形能力的影响程度。

基于上述研究，课题组为了进一步研究HDC加固受损混凝土短柱轴压试验，通过增大加固柱的截面尺寸和高度，继续研究相对于前期试验，增大柱截面尺寸和高度下HDC加固受损混凝土短柱的变形和承载能力，为HDC加固技术在混凝土短柱受损后的修复与加固提供更加详实的理论基础和试验依据。

1 试验概况

1.1 试验设计与处理

本次试验一共有9根相同的钢筋混凝土柱，并编号ZZ-1～ZZ-9。考虑到本次试验为轴压试验，为避免在轴压试验下短柱截面应力分布不均的情况，本次试验采用短柱。研究表明[11]，当混凝土柱在长细比力l/b>2时，柱体抗压强度的降低幅值已变化很小，故取短柱长细比为5，保证试件破坏为强度破坏。试件的尺寸为240 mm×240 mm×1 200 mm，纵筋采用配筋率为0.6%的4根直径长为12 mm的HRB335级热轧钢筋，箍筋采用HPB300级钢筋，直径为8 mm。原混凝土强度等级为C35。本试验混凝土柱截面尺寸及配筋图，如图1所示。钢筋的测试强度，如表1所示。

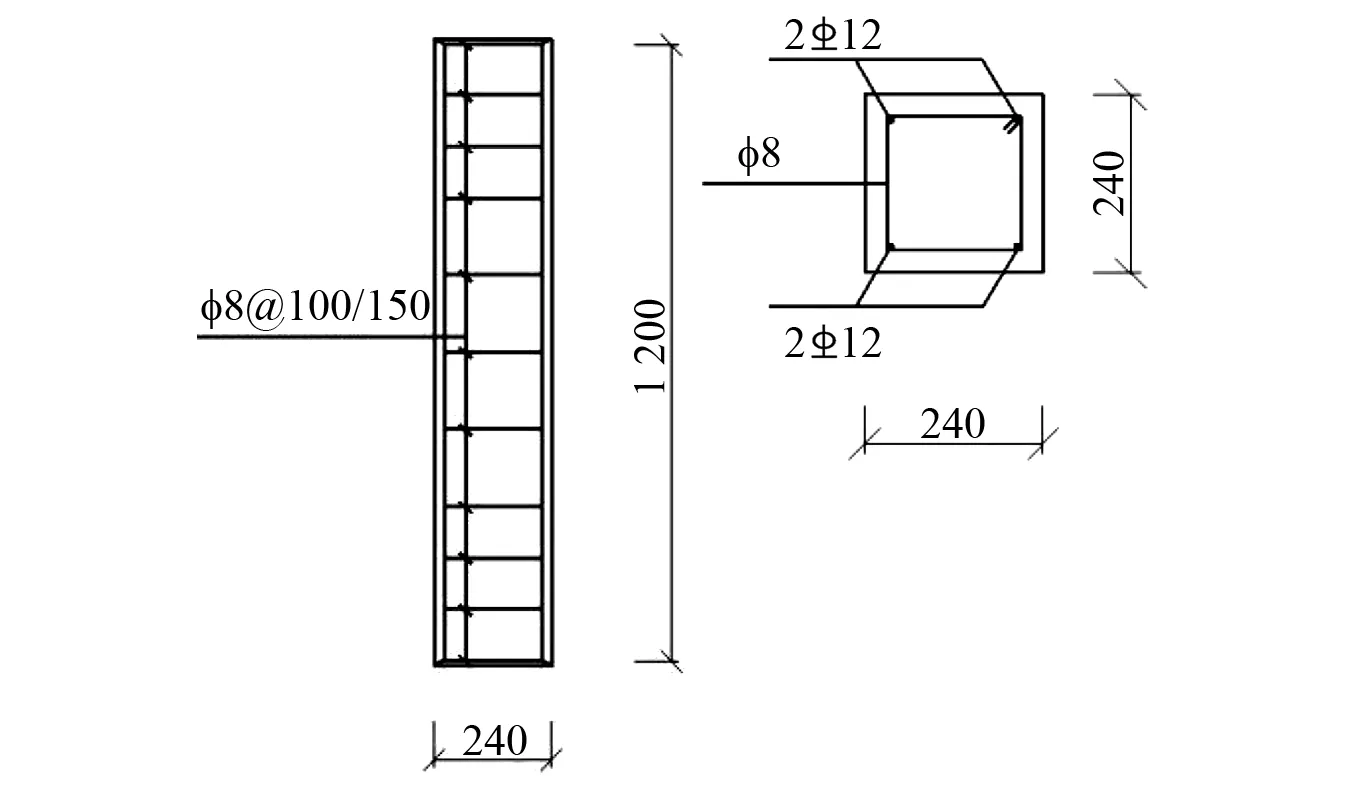
图1 原试件几何尺寸及配筋(mm)Fig.1 Dimensions and reinforced details of original specimen(mm)

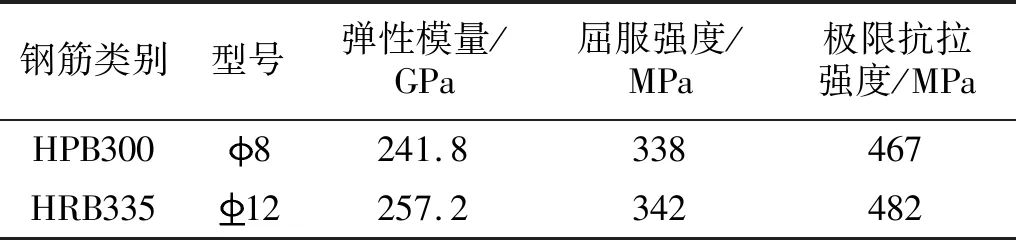
表1 钢筋基本参数指标Tab.1 Basic mechanical properties of steel bars

为研究受损混凝土短柱的HDC加固效果，课题组先后进行了两次试验。第一次试验先对9个未受损的混凝土短柱进行轴压试验，试验结果表明随着荷载的逐渐增加，试件从出现裂缝到完全破坏的时间很短，混凝土的延性很差，混凝土被压碎大块脱落，破坏属于典型的脆性破坏。第二次试验开始前，先将第一次试验受损的混凝土短柱进行表面处理。首先用铁锤、凿子将受损柱损伤部位进行凿毛处理，露出混凝土的粗骨料，为保证混凝土与HDC的黏结，混凝土柱身表面也需进行凿毛处理。再用气枪将构件表面的尘土碎屑清除，最后用高压水枪冲洗混凝土柱身表面。处理完受损构件后，采用HDC进行加固，加固层厚度为20 mm。

1.2 材性试验

课题组采用HDC作为试验的加固材料，其配合比砂∶水泥∶粉煤灰∶水∶减水剂 =0.72∶1∶1∶0.58∶0.03。在本次试验所用的HDC中，砂子为陕西灞河河砂，最大粒径为1.18 mm，水泥为铜川某公司的P.O 42.5R普通硅酸盐水泥，粉煤灰级别为一级，产自陕西大唐某发电厂，减水剂采用聚羧酸系高效减水剂。HDC中所掺加的聚乙烯醇(Polyvinyl Alcohol,PVA)纤维为日本可乐丽公司生产的KURARAY K-II纤维，掺量所占体积分数为2%，其性能指标如表2所示。试验前对HDC材料进行了力学性能测试加载装置详见图2。其中，抗压试块为100 mm×100 mm×100 mm的立方体试块，抗压强度如表3所示。抗拉试块为哑铃型，抗拉强度如表4所示。

表2 PVA纤维性能指标Tab.2 Performance indicators of PVA fibers

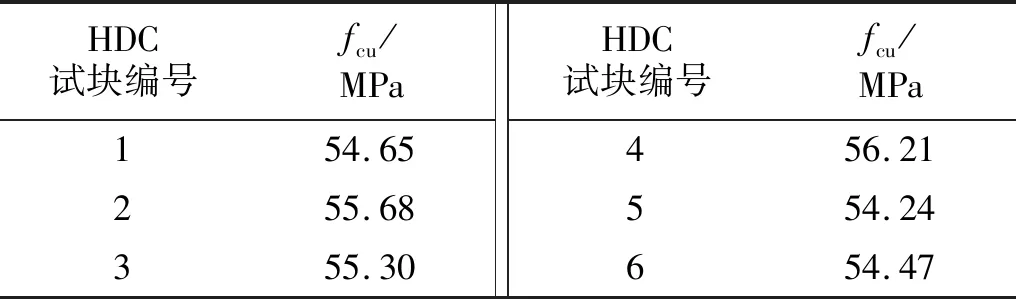
表3 HDC试块抗压强度测试Tab.3 Test results of compressive strength of HDC

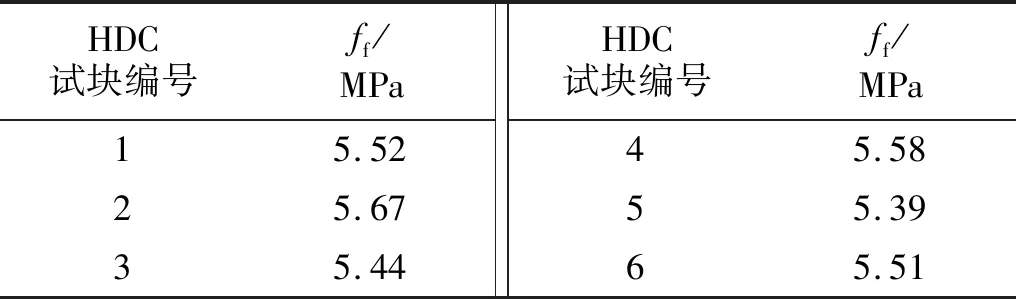
表4 HDC试块抗拉强度测试Tab.4 Test results of tensile strength of HDC

图2 HDC试块抗压试验Fig.2 HDC test block compression test

1.3 加载方案和加载装置

试验在液压伺服试验机上进行，型号为YAW-5000F。加载装置图参如图3所示。本次试验所有构件均为轴心受压试验。在加载初期先进行50 kN的预加载，当试件荷载达到50 kN后，再采用等位移进行连续加载，加载速度变为0.1 mm/min，当试件达到最大荷载Fmax后，加载速度改为0.2 mm/min，当荷载下降至0.6Fmax时，停止加载。试验过程中试件的轴向荷载由压力传感器测量，数据采集仪系统自动采集变形数据，为了测量试件的纵向变形，在液压伺服试验机下部底座上安装一个位移计，同时在每个试件相邻的侧面中间部位各装置一个位移计，用以测量试件的横向变形。

图3 试验加载装置Fig.3 Test setup

2 试验现象及结果分析

2.1 试验现象和破坏形态

对于未受损混凝土短柱，在荷载加载初期，柱身表面没有较明显变化。随着荷载的不断增加，柱子每个侧面均出现了竖向发展的细微裂缝，裂缝较多集中于柱子顶部。随着荷载的持续增加，柱顶部的细微裂缝慢慢扩大且向柱身中部顺延，与此同时柱身混凝土也开始出现侧向膨胀。在此阶段裂缝细而少，当接近峰值荷载2 000 kN时，裂缝开始迅速发展，竖向裂缝扩大且不断增多，并有清脆的断裂声，继续持荷会发现大的裂缝之间有相互贯通的现象，混凝土随着裂缝的不断开裂开始大块脱落，伴随着较大的声响，混凝土短柱被压坏。从开始持荷到柱子被压坏的时间较短，这是典型的混凝土脆性破坏。

对于加固柱，为了便于分析HDC的加固效果，将柱身的4个侧面分为东南西北4个面(每个柱取其相应的东南西北，不固定)。现取ZZ-1具体分析：当持荷到699 kN时，加固柱西面顶端开始出现第一条长为3 cm的竖向细微裂缝，此时短柱的纵向位移为2 mm，横向位移并没有较明显的变化，由于核心混凝土的横向变形较小，HDC的约束作用还未完全体现出来。随着荷载的持续增加；当持荷到850～900 kN时，在柱子南面和北面也相继出现细微裂缝，出现的裂缝都较为集中在柱子顶端与中上部；当持荷到2 015 kN时，东面的第一条裂缝周围出现多条横向细微裂缝，随之南面也出现横向裂缝，随着荷载的增加，加固面层表面的竖向裂缝或者斜向裂缝和横向裂缝明显开始延伸和增多；当持荷到峰值荷载2 565 kN附近时，加固柱北面底部开始出现裂缝，最长一条长达23 cm，此时，加固柱的纤维持续撕裂，并且发出“沙沙”的声响，达到峰荷载后，承载力开始逐渐下降；当荷载下降到2 250 kN时，东面的裂缝开始贯通，形成一条长约67 cm的竖向裂缝，裂缝宽度为4 mm，并且裂缝由东面中部延伸到南面，此时加固柱已开始破坏；当荷载下降到1 812 kN时，北面底部的裂缝延伸到西面随之又与东面贯穿最后延伸至东面顶部，此时加固柱已完全被破坏。破坏时由底角首先开裂并形成贯穿柱身的整个贯穿通缝，由于HDC的约束作用，并未出现混凝土剥落的现象，而且由于HDC的加固，达到峰值极限荷载后，荷载下降的缓慢，表现出极好的延性。

试件ZZ-3，ZZ-4，ZZ-5，ZZ-6，ZZ-9的初裂荷载与ZZ-1相近，在576～690 kN，裂缝的初期发展均较为集中在柱子的中上部，裂缝较为细微且发展缓慢。裂缝在中后期的发展表现为靠近底部的裂缝随着荷载的增大不断开裂并向上延伸，其中ZZ-2，ZZ-3与ZZ-4的破坏是由于柱身底部的裂缝向上延伸至柱身中下部，横向裂缝与纵向裂缝使得HDC面外鼓致使约束力丧失导致破坏，如图4所示。ZZ-1，ZZ-5与ZZ-6最终的破坏是由于底角的裂缝向柱上延伸并贯穿整个柱身，使得HDC面层开裂导致约束力丧失而破坏；ZZ-9的破坏是由于底部的裂缝延伸至柱身中部，以及柱身底部裂缝开裂使得HDC的面层开裂外鼓，是得HDC的约束作用丧失造成破坏。

ZZ-7与ZZ-8的初裂荷载基本相同，均在580 kN左右出现，裂缝的初期发展均在柱中上部。但与ZZ-1不同的是，ZZ-7与ZZ-8下部裂缝发展趋势缓慢，中上部裂缝较之下部发展较多，最终破坏是由中上部裂缝横向相互贯通导致柱发生破坏。造成各试件破坏的主要裂缝，如图4所示。

图4 试件破坏性裂缝Fig.4 Destructive crack of test piece

加固柱的初裂荷载均在560～700 kN，峰值荷载也达到了2 400 kN以上。整个破坏过程裂缝发展的趋势大致相似，首先出现的裂缝大都集中在柱身中上部，初始裂缝均为细微裂缝。加固柱最终的破坏主要原因为裂缝贯通导致HDC的约束能力降低，致使核心混凝土压碎导致破坏。与未加固柱不同，初始裂缝随着持荷的增加发展较为缓慢，这是由于HDC良好的裂缝控制能力与延性。加固柱最终的破坏均是由角部裂开形成贯穿柱身的通缝，但并无脱落现象。在加固柱被压坏后卸荷，将HDC外层凿开查看破坏后的核心混凝土，发现尽管混凝土有酥碎现象，但其形状基本保持较好，这是由于HDC与混凝土之间良好的黏结能力，并且有效的约束混凝土的横向变形和侧向膨胀。各轴压柱加固前与加固及加固破坏后剥开的试验现象，如图5所示。

2.2 应力-应变曲线分析

本次试验HDC加固受损混凝土短柱的具体结果如表5与表6所示。从应力应变图6可以较直观的看到，在加载初期，由于荷载较小，试件处于弹性阶段，未加固试件与加固试件在此阶段的应力上升趋势基本是一致的。HDC材料本身的性能，加固后能够较大幅度提高构件的延性和承载力，这在应力应变曲线图中也得到明显的验证。

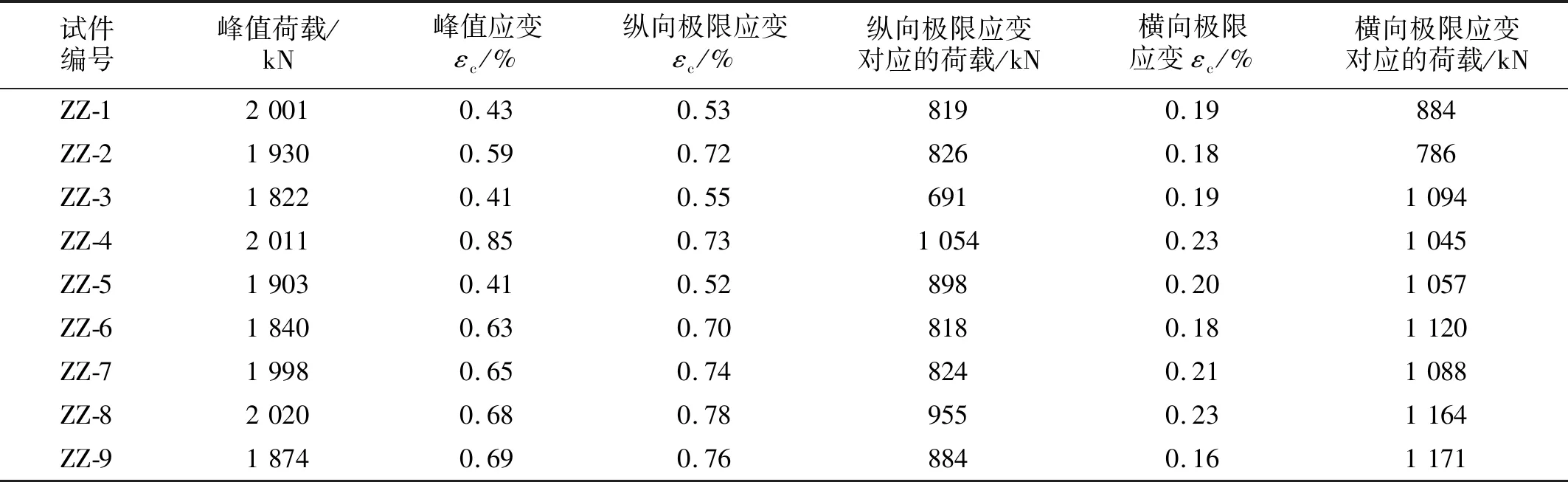
表5 未加固受损混凝土短柱试验结果Tab.5 Test results of unreinforced damaged concrete short columns

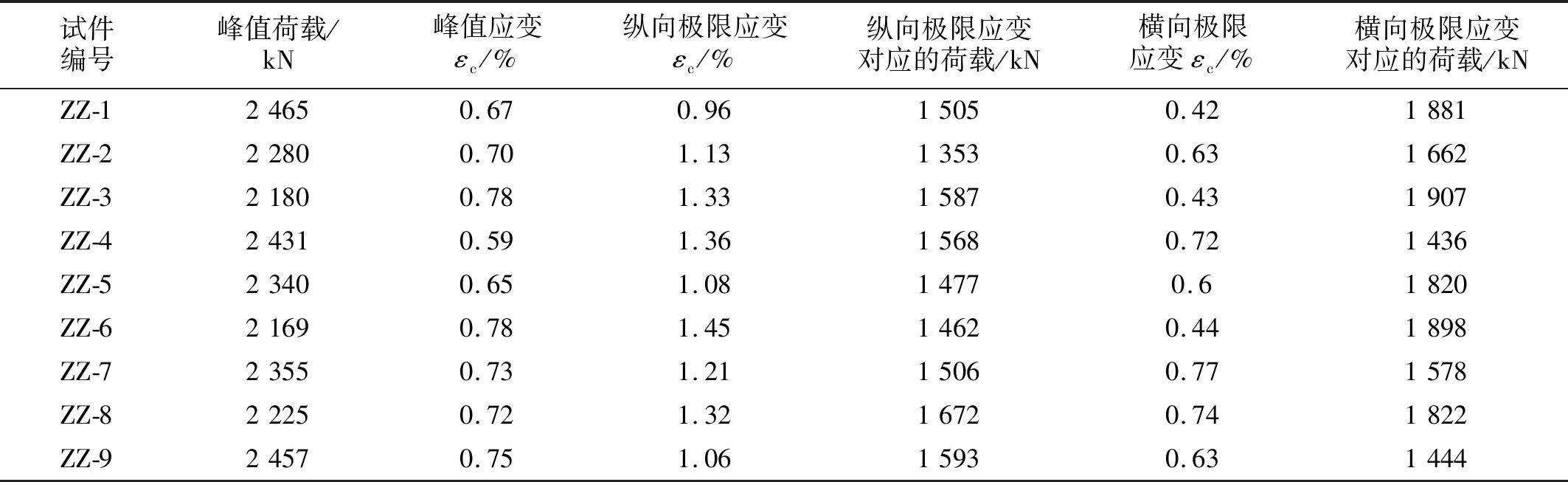
表6 HDC加固受损混凝土短柱试验结果Tab.6 Test results of HDC reinforced damaged concrete short columns

2.2.1 试件应力分析

由应力应变曲线可以得到，未加固混凝土短柱的峰值应力在34 MPa左右，加固前混凝土短柱虽已受损，但加固后的峰值应力仍可达到原有混凝土柱的80%～90%。加固后原柱截面面积增大，峰值应力相对原柱较小，但峰值荷载均有不同程度的提高。原柱峰值荷载在1 800～2 000 kN，HDC加固后的短柱峰值承载力可达2 180～2 465 kN，峰值荷载提高了约10%～31%。加固前的混凝土短柱属于脆性破坏，其应力达到峰值后迅速下降，而加固后的混凝土短柱由于HDC材料的特性，在达到峰值应力时仍能保持较大的延性和承载力。相应地，加固前的破坏极限应力为12～18 MPa，加固后的破坏极限应力可达到17～20 MPa，加固后比未加固的极限应力大部分可提高约30%左右。

2.2.2 试件应变分析

HDC材料的优良特性使得试件的应力得到较大的提高，对于试件的应变也有较大的提高。对于未加固试件，其纵向峰值应变为0.41%～0.69%，加固后的纵向峰值应变达到0.59%～0.78%，相比未加固试件，加固后的试件纵向峰值应变均有不同程度的提高，最高可达90%。

与纵向应力相似，加固前混凝土短柱的脆性破坏使得试件在达到峰值应变后迅速下降，纵向极限应变为0.52%～0.78%，HDC加固后的试件具有良好的延性，曲线在达到峰值之后下降缓慢，对比未加固试件，纵向极限应变可达到0.96%～1.45%，提高约47%～141%。HDC加固后的混凝土短柱不仅延性得到较大提高，极限荷载也有很大提高。加固前混凝土短柱纵向极限应变对应的荷载为691～1 054 kN，HDC加固后对应的荷载为1 353～1 672 kN，提高了48.7%～129.0%。

与纵向应变相比，试件的横向应变比纵向应变变化较早。未加固试件的横向峰值应变为0.085%～0.190%，HDC加固后的试件，在构件未到达峰值应力时横向应变几乎不明显，横向峰值应变为0.058%～0.220%。由于HDC掺加了纤维，与混凝土之间具有很好的黏结力，加固层能够有效的约束核心混凝土的横向变形，因此加固后试件的横向极限应变较加固前的极限应变大很多，相应的横向极限应变对应的荷载也有较大提高。加固后的试件横向极限应变可达到0.42%～0.77%，而未加固的试件极限横向应变为0.16%～0.23%，加固后的极限横向应变约为加固前的2倍～3倍。加固前的横向极限应变对应的荷载为786～1 171 kN，HDC加固后对应的荷载为1 436～1 907 kN。提高了约23%～112%，大部分提高较为明显。轴心受压应力应变曲线图，如图6所示。加固后的纵向和横向应力应变曲线对比图如图7和图8所示。

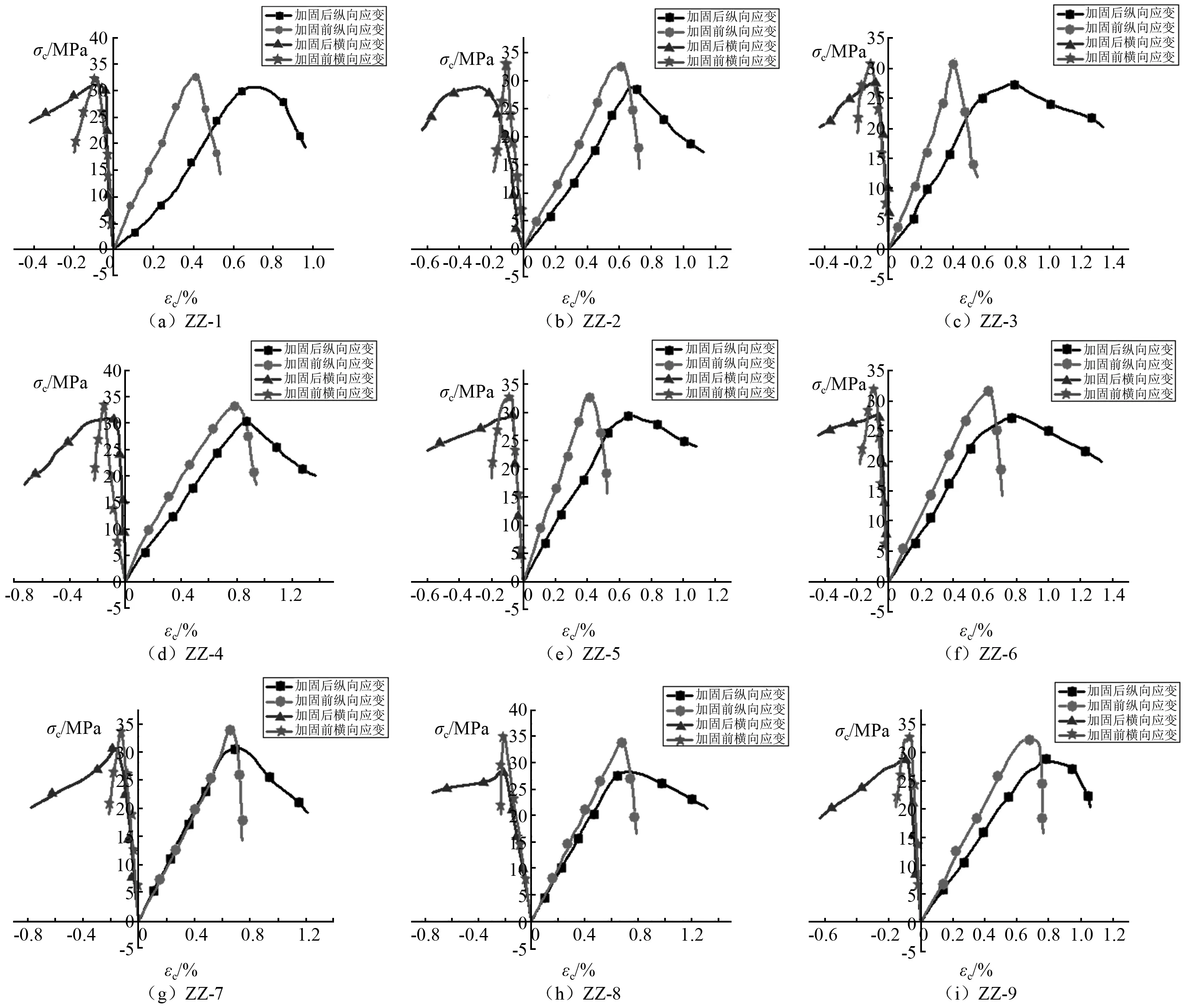
图6 轴心受压应力-应变关系曲线Fig.6 Stress-strain curve of axial compression

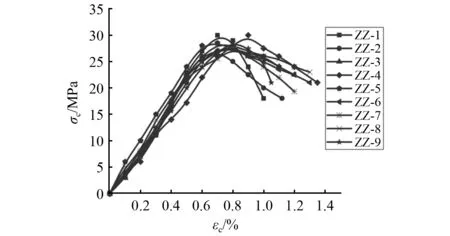
图7 加固后纵向应力-应变关系曲线Fig.7 Stress-strain curve of axial compression

图8 加固后横向应力-应变关系曲线Fig.8 Stress-strain curve of axial compression

3 应力-应变曲线公式拟合

3.1 纵向应力-应变曲线拟合

参照陈宗平等的研究，将图7纵向应力应变曲线进行归化处理，即除以对应的峰值应力与应变，消除参数影响，如图9所示。由此拟合出应力应变全过程经验公式，如图10所示。为了描述试验过程，可将图10分为弹性阶段、弹塑性阶段，下降阶段3个阶段，拟合出数学表达式如式(1)所示。

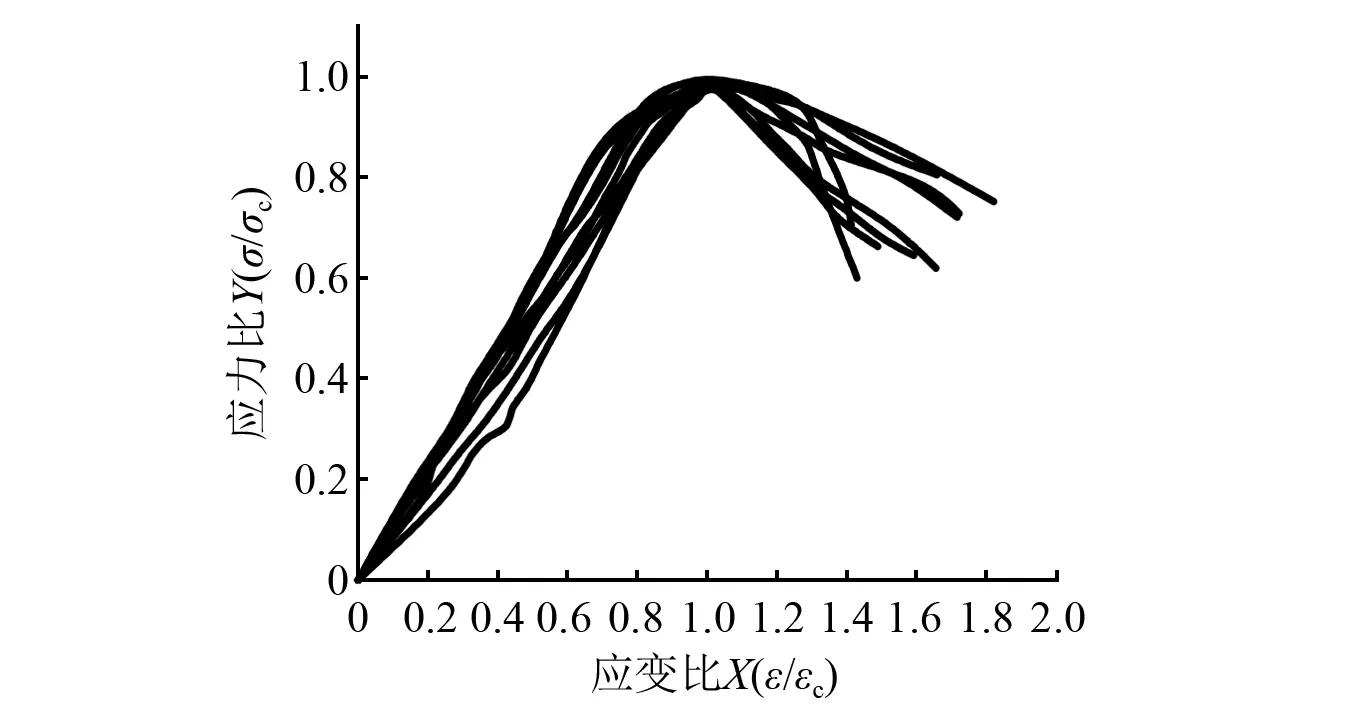
图9 纵向应力-应变试验经验曲线Fig.9 Test curves of longitudinal strain-stress

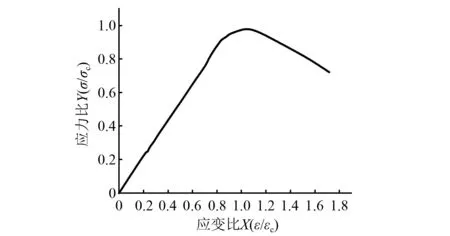
图10 拟合纵向应力-应变全曲线Fig.10 Fitting curve of longitudinal strain-stress

(1)

式中:x1=ε/εc和y1=σ/σc;A为弹性阶段参数，xA为比例极限对应的应变与峰值应变比值，通过试验数据拟合，取A=1.08，xA=0.8;xB为下降段极限对应的应变与峰值应变比值，取1.7。

通过对HDC加固短柱工作机理与以往ECC加固混凝土柱研究，将式(1)进行化简归纳分析，进一步得到式(2)。

式中，K=σc/εc为加固后HDC纵向峰值应力比上对应的峰值应变。拟合后的纵向应力应变曲线与试验应力应变曲线比较，如图11所示。

图11 试件纵向试验曲线与理论计算曲线对比Fig.11 Comparison between the longitudinal test curve and the theoretical calculation curve

结果表明按照式(2)计算的HDC加固后纵向应变轴心受压应力-应变曲线与本次试验结果较为吻合。

3.2 横向应力-应变曲线公式拟合

采用相同方法对加固后的横向应力应变进行归化处理，如图12所示，对规划处理后的曲线进行拟合，如图13所示。由于HDC的约束作用与破坏机理，拟合后的曲线分为弹性阶段与弹塑性阶段两个阶段，拟合出的数学表达式如式(3)所示。为便于与轴心受压应力应变曲线对比，仍取横坐标为负值。

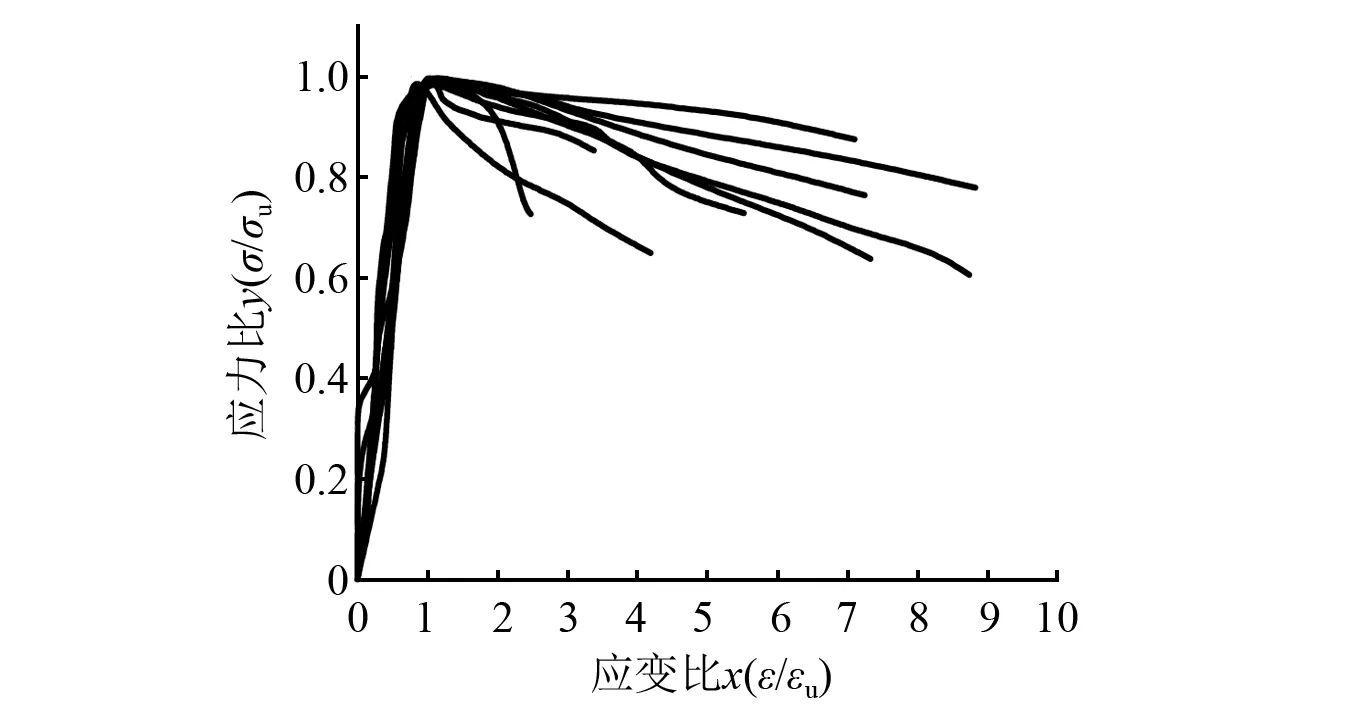
图12 横向应力-应变试验曲线Fig.12 Transverse stress-strain test curve

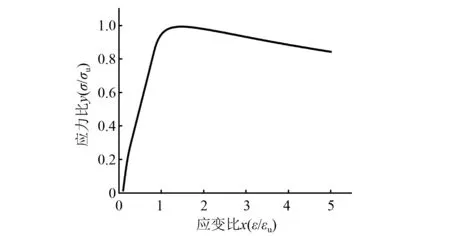
图13 拟合横向应力-应变曲线Fig.13 Fit the transverse stress-strain curve

(3)

式中：x2=ε/εu和y2=σ/σu;B为弹性阶段参数，xc为弹塑性阶段极限对应的应变与峰值应变比值，通过试验数据拟合，取B=1，xc=5.5。类比纵向应力应变曲线，对式(3)进行归纳化简分析，得到式(4)。

(4)

式中，k=σu/εu为加固后HDC横向峰值应力比上对应的峰值应变，拟合后的横向应力应变曲线与试验应力应变曲线比较，如图14所示。计算结果与试验结果较为吻合。

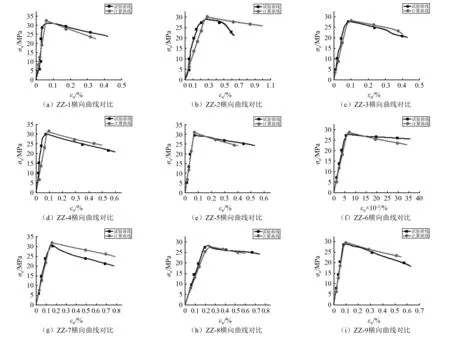
图14 试件横向试验曲线与理论计算曲线对比Fig.14 The transverse test curve of the specimen is compared with the theoretical calculation curve

4 HDC加固受损混凝土短柱正截面承载力分析

4.1 HDC加固混凝土短柱加固机理分析

本次试验研究的重点是原柱在受损破坏情况下采用HDC加固后，受损混凝土短柱的承载力与原柱的比较分析。从2.1节的试验现象可得，未加固混凝土柱的破坏是由于柱身内部骨料与砂浆在接触面上有细微裂缝，在承受轴压荷载时，裂缝不断沿着应力方向产生和扩张的结果，最终产生的裂缝将试件分成了许多小柱然后向外鼓出导致试件破坏[12]。由2.1节的破坏机理可知，混凝土短柱在轴压作用下，如果同时在承受侧向压力，外侧约束层能够对柱身提供一系列弹性支撑，使得松散鼓出的小柱能够互相挤压靠拢，已经开裂的部分有重新闭合趋势，从而增强了试件的刚度、延性和强度。HDC加固混凝土短柱的作用机理就是与此相近，通过在受损混凝土短柱外部包裹一层HDC来约束核心混凝土的变形，使得核心混凝土处于三向受压的状态，加之HDC本身就有良好的抗裂性能和强度，可以较好的提高试件的延性和承载力。

顶岗实习作为人才培养重要的一环，学生实习的行业分布、地区分布、岗位分布情况对学院专业人才培养方向确定、学生就业工作起着重要的指导作用，但是这些信息没有被学校及时的收集整理，也没有被分析，顶岗实习资料、文档收集散乱，不利于管理的科学化、规范化。

4.2 正截面承载力的理论推导

4.2.1 已有计算公式的分析

考虑到本次试验中的加固方案，可类比增大截面法加固轴心受压混凝土短柱来计算HDC加固混凝土短柱的承载力。参照我国GB 50367—2013《混凝土结构加固设计规范》[13]中增大截大面法加固钢筋混凝土结构的计算公式，课题组发现，规范中给定的承载力计算公式只是建立在经验基础上，简单的将新、旧混凝土承载力进行叠加，然后引入一个折减后的共同工作系数来作为全截面的承载力，但是加固的结构属于二次组合结构，HDC加固层与原柱存在整体共同受力的问题，并且一般情况下黏接面的黏结强度远低于原混凝土的强度，这些因素就决定了加固后的试件不能简单按照规范中给定的经验公式进行计算。规范给出的增大截面法加固钢筋混凝土柱简化计算公式为

式中，αcs为对新增混凝土和钢筋强度利用程度综合考虑后的修正系数，规范中令αcs取0.8。公式中并没有考虑到加固材料即外包HDC对短柱核心混凝土强度的增大作用，为了能够更为准确且贴合实际地计算出加固后混凝土柱的承载力，需要对规范现有的公式进行改进，引入外部HDC对内部核心混凝土强度增大系数和HDC加固混凝土的强度利用系数。

4.2.2 正截面承载力的计算假定

在推导HDC加固受损混凝土短柱的正截面承载力的理论计算公式时，首先进行如下假定：

(1)HDC与混凝土结合面之间黏结可靠，二者在共同受力时能共同工作；

(2)加固后的截面仍为平截面；

(3)不考虑加固后HDC与原混凝土的收缩、温度和徐变的影响；

(4)原柱的混凝土应力应变关系采用Hognestad模型计算公式为

4.2.3 外包HDC对核心混凝土柱的约束作用

由4.1节的加固机理可知，外包HDC加固混凝土柱，使得混凝土柱处于三向受压状态，以此产生的约束力来约束核心混凝土的变形。参考文献[14]，对于圆柱形的截面，外包HDC约束核心混凝土后的强度可用下列公式计算：σT=fc1+4.1σH，σH为外包HDC所提供的约束力。

当外包HDC表面有纵向裂缝出现时，HDC对核心混凝土的约束作用已经失效。因此，外包HDC所提供的横向约束力可按图15的平衡方程求得。

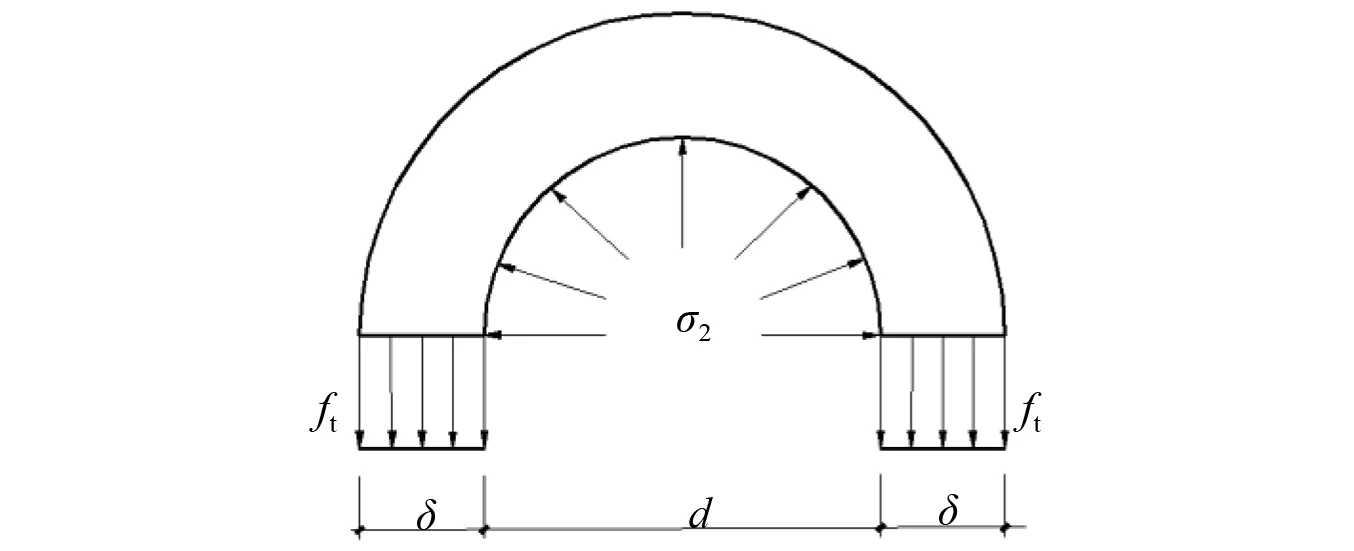
图15 圆形截面图Fig.15 Circular cross section

(5)

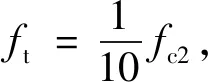
(6)

考虑到HDC约束核心混凝土后，相应内核混凝土强度提高为

(7)

将式(7)进行化简，可得

(8)

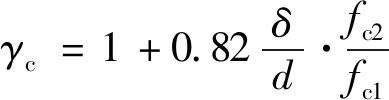
σT=γcfc1

(9)

本次试验的试件为混凝土方柱，为了使式(9)更为符合本次试验，需要对图15圆形截面图进行换算，可按图16中的内接圆阴影部位进行换算。换算需考虑约束作用的降低，进行折减，折减系数ψ可参考文献[15]取ψ=0.8，则外包HDC矩形截面约束核心混凝土强度提高为

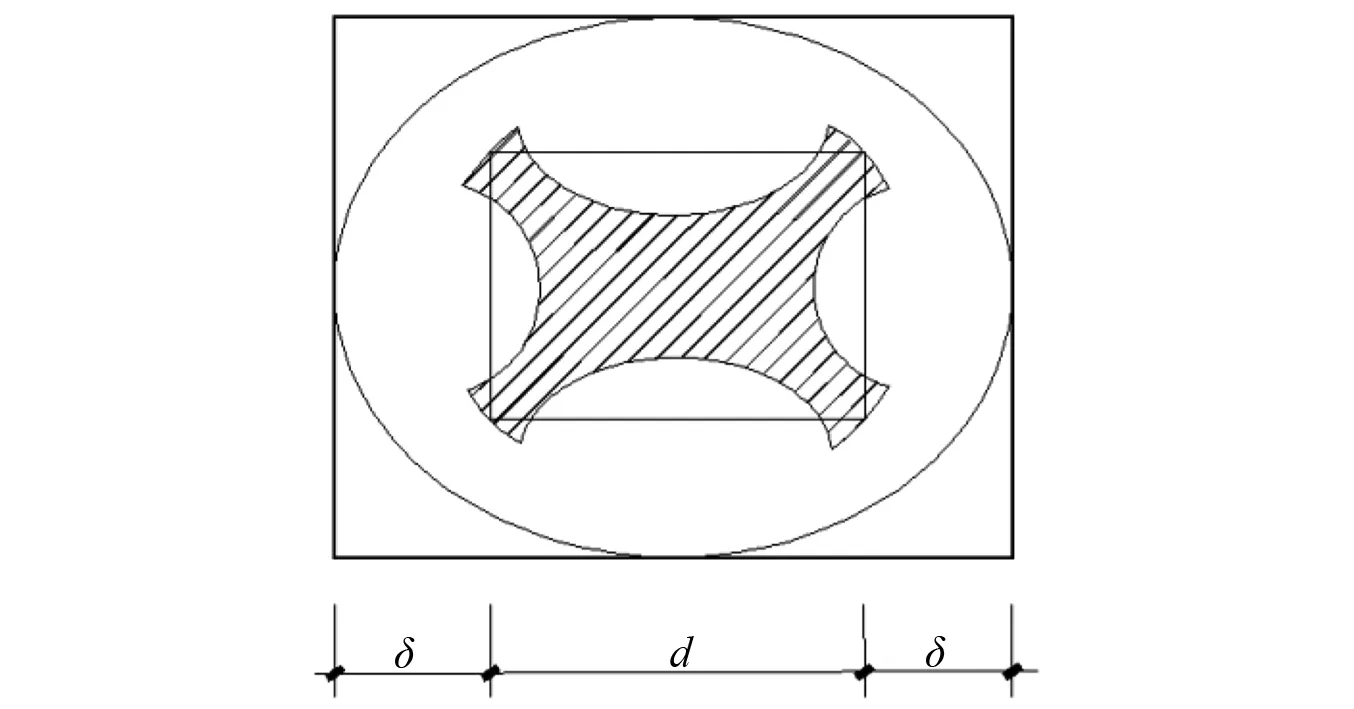
图16 矩形截面图Fig.16 Rectangular cross section

(10)

化简可得

(11)

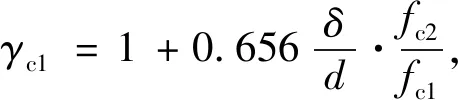
σT=γc1fc1

(12)

式中，γc1为核心混凝土强度提高系数。

4.2.4 HDC加固核心混凝土强度利用系数

外包HDC强度利用系数，是在二次受力下，根据新旧混凝土之间的应力应变差计算得出。在实际工程中，因承载力不足时对结构进行加固，新加固的混凝土与原有的混凝土会存在应变滞后现象。考虑到在二次受力构件的极限状态下，新增混凝土的应力值取决于加固前原柱混凝土已有的压应变与混凝土的极限应变差值，差值越大，新混凝土的应力值就越大。实际工程中，很难对拟加固构件进行完全卸荷，因此在实际工程中加固构件基本为二次受力构件。本次试验旨在研究HDC加固受损混凝土短柱后的承载力，也为了HDC能够适用于实际工程中去，所以引入加固HDC强度利用系数，使承载力公式更能满足实际需要。

国内众多学者对二次受力下增大截面法加固混凝土柱的研究已经很充分了，参照相关研究[16-18]，考虑在二次受力情况下，根据基本假定，轴心混凝土的应力应变关系可以表示为

(13)

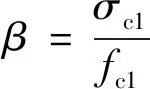
当核心混凝土压应变达到其极限应变时，核心混凝土应变增量

Δεc1=εc1-ε1

(14)

由于HDC加固混凝土短柱在达到其峰值应变之前横向应变发展较为缓慢，加固层约束的作用不明显，同时根据相关研究[19]，密布箍筋约束混凝土的应力应变曲线与素混凝土应力应变曲线的形状相同，HDC约束混凝土与密布箍筋约束混凝土一样，都是εc1通过约束核心混凝土的横向变形来提高核心混凝土的强度，因此可以近似认为在达到峰值应力之前HDC加固混凝土柱与素混凝土的受力特点相近，HDC的压应力仍可参照混凝土的本构，即相应HDC的压应力为

(15)

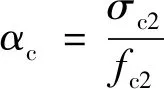
(16)

将式(14)代入式(16)中，得

4.3 轴心加固柱的正截面承载力计算

根据理论分析以及推导，改进后的轴心受压正截面承载力计算公式为

(17)

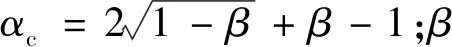
考虑到加固前原柱在达到极限承载力状态时，钢筋已经屈服，参照有关研究[20]钢管混凝土内含钢率对剩余承载力影响并不明显，为更符合实际，取钢筋强度的60%作为钢筋剩余强度。在本次试验中，应力水平指标为0，则最终正截面承载力计算公式为

(18)

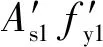
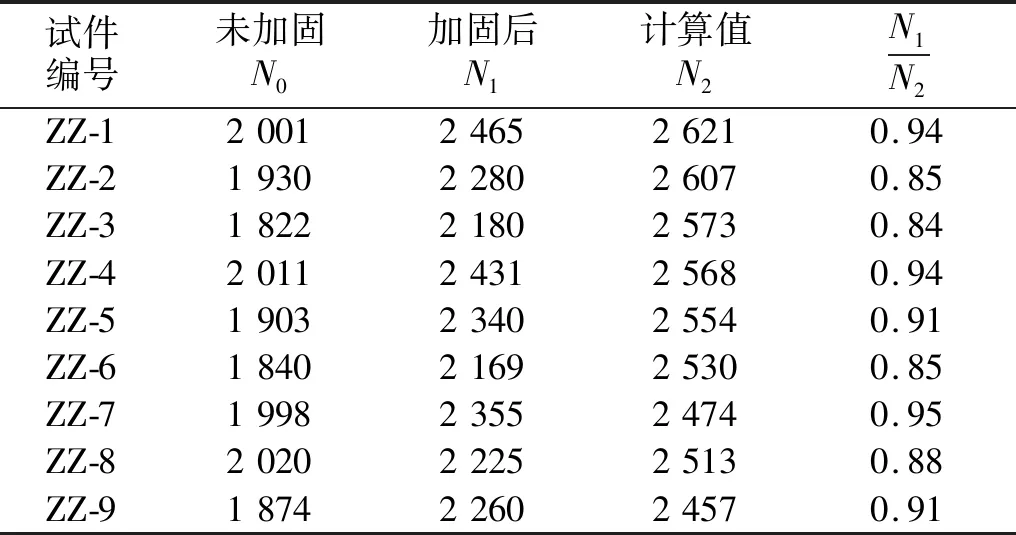
表7 试验和计算结果对比Tab.7 Formula calculation results

由表7可知:计算值与实际值误差均值在10%左右，公式与实测值吻合较好。表中计算值相对于实际值较高，这是由于平截面假定并未考虑HDC与原有混凝土之间的黏结问题。

5 结 论

本次试验通过对9个受损混凝土短柱采用HDC加固，并进行轴心受压试验，对HDC加固后的受损混凝土短柱进行力学性能分析，得到如下结论：

(1)得益于HDC良好的裂缝宽度控制和黏结能力，采用HDC加固受损混凝土短柱能有效提高混凝土短柱的变形能力和承载力，并增加结构的使用寿命。这与HDC的理论研究结果相吻合，同时也验证了HDC用于工程加固的可行性。

(2)在对HDC加固后的混凝土短柱进行轴心受压试验时，HDC的裂缝控制能力和约束核心混凝土的变形能改善混凝土短柱的脆性性能，较大程度提高混凝土柱的延性，运用于实际工程中能够提高构件的安全稳定性。

(3)通过对比未加固与加固混凝土短柱应力应变曲线可发现——相对于未加固混凝土短柱，HDC加固后混凝土短柱峰值应力可达到原柱的80%～90%，极限应力提高了30%左右。加固后的试件具有良好的延性，因此纵向极限应变提高幅度较大，可达到47%～141%。由于加固层有效的约束核心混凝土横向变形，使得试件的横向极限应变较加固前的极限应变大很多。加固后的试件横向极限应变可达0.42%～0.77%，而未加固的试件极限横向应变为0.16%～0.23%，加固后的极限横向应变约为加固前的2倍～3倍。

(4)提出HDC加固后纵向与横向应力应变曲线全过程曲线公式，试验实测曲线与理论计算曲线拟合较好。

(5)基于混凝土短柱的破坏机理与三向受压约束核心混凝土等理论，参照规范并引进相关系数，考虑实际工程情况，推导出了改进后的承载力公式。将理论结果与试验结果相对比，公式计算结果与试验结果吻合良好，可以运用于实际工程中。