基于CEEMD与自适小波阈值组合降噪在OPAX方法的应用

陈 克，张晓冬，李 宁

(1.沈阳理工大学 汽车与交通学院，沈阳 110159;2.辽宁省汽车噪声振动和安全工程技术研究中心，沈阳 110159)

扩展工况传递路径分析(operational path analysis with exogeneous inputs，OPAX )方法是Janssens等[1]综合了传统传递路径分析方法周期长与工况传递路径分析方法的精度差的问题所提出的改进方法。该类方法基于传递路径分析理论，其目的是找到振动源对车内目标点影响最大的路径，同样目标点的总响应是来自不同位置的路径的总贡献量线性叠加得到的，即目标点的实测响应等于合成响应。同时该方法搭建参数化模型时需要大量的汽车工况数据(时域振动信号)，这些信号是在汽车工况状态下测试的，信号难免掺杂噪声，从而影响每条路径的贡献量计算精度。针对此类问题，莫愁等[2]运用小波阈值降噪对OPAX方法进行降噪处理，并且结合模糊神经网络与逆子算法提高模型精度。潘公宇等[3]对小波的阈值选取以及阈值量化规则进行改进且进一步提高OPAX方法分析精度。

工况数据复杂且庞大，单纯的小波降噪精度有些欠缺，因此本文引入组合降噪方法。组合降噪方法中，互补集合经验模态分解(complementary ensemble empirical mode decomposition，CEEMD)与小波组合效果较好，CEEMD是Yeh等[4]改进集合经验模态分解(ensemble empirical mode decomposition，EEMD)重构精度问题所提出的。该组合降噪是将信号先经过CEEMD分解成不同的本征模态分量(intrinsic mode function，IMF)后，再对各个含噪的IMF进行小波阈值处理，提高降噪后信号的精度。该类方法中，周涛涛等[5]采用排列熵估计出CEEMD分解后的各个IMF分量的含噪情况并且进行降噪；王亚萍等[6]对比了EEMD与CEEMD方法的效果，应用相关性判定各个分量的含噪量，并提出CEEMD与小波半软阈值结合的降噪方法对含噪区间进行处理效果较优；石大磊等[7]从白噪声各个IMF分量的能量密度与平均周期的乘积是一个常数的角度去判断各个分量的含噪情况，通过改进的小波半软阈值函数给予含噪区间相应的降噪处理。

上述3种方法对于分解后的IMF分量的筛选都提出了方案，但对于阈值降噪来说，阈值函数的选取至关重要。周涛涛等的研究没有对阈值函数进行改进，王亚萍等和石大磊等仅运用了半软阈值以及其改进型来完善降噪效果，且对于每个含噪分量都用一样的阈值函数处理，缺乏自适应性。本文将从这方面入手与样本熵结合提出一种CEEMD与自适小波阈值组合降噪的方法，通过仿真检验降噪效果并且运用到搭建OPAX方法模型工况数据的降噪上，最后通过验证目标点合成响应与实测响应的一致性间接的检测分析精度提升效果。

1 样本熵改进的CEEMD小波组阈值合降噪方法

1.1 CEEMD分解

CEEMD分解先向原始信号中加入N次正负相反的且均值为零的白噪声，其中一组为

(1)

式中:F1(t)和F2(t)分别为原始信号y(t)、加入的噪声信号n(t)和相反的噪声信号-n(t)，总体的信号为2N个。

对这2N个信号都进行集合经验模态分解并将对应的IMF分量加和求平均，得到第jj个IMF分量，即

(2)

式中:Ijj(t)为第jj个IMF分量;cij(t)为第i个信号、第j个IMF分量。经过CEEMD分解后，信号等于各个IMF分量与余项的加和，即

(3)

式中，r(t)为余项；IMF分量的个数有n个。

分解得到的Ijj,(jj=1,2,…,n)分量以及余项的噪声含量基本不同，为了量化每个IMF分量的含噪情况方便给于每个分量较优的处理方式。因此引入样本熵作为信号含噪程度的量化标准。

1.2 样本熵在该方法的应用

样本熵是一种新的时间序列复杂度的表征参数[8]。对于长度为N的时间序列Ai={a1，a2，…，aN}其样本熵有

(4)

式中:m为嵌入维度；r为相似容限值，一般情况下r=0.1～0.25std(其中std为时间序列Ai的标准差)；X(m)(r)为在m维度上时间序列的间距小于r的个数总合；Y(m)(r)为在m+1维度上时间序列的间距小于r的个数总合。

噪声信号的无序性较大，且所含的信息量较少，其样本熵较大；有用信号规律性较强，其样本熵较小[9]。

取维度m=2，相似容限值r=0.2std，计算原始信号s(t)样本熵为Ss(t)，以及Ijj,(jj=1,2,…,n)分量和余项r(t)的样本熵为SIjj和Sr(t)。

定义Ii(i=1,2,…,x)为噪声分量，该分量噪声含量极大，几乎不含有用成分；定义Ij(j=1,2,…,y)为含噪分量，该分量含有噪声成分与有用成分；定义Ik(k=1,2,…,z)为信号分量，该分量基本都是由有用成分组成的，余项r(t)可以直接视作有用成分(属于信号分量)。

处理时，直接剔除噪声分量Ii(i=1,2,…,x)，对含噪分量Ij(j=1,2,…,y)实施降噪处理，信号分量Ik(k=1,2,…,z)则直接与降噪后的含噪分量一起重构成最终降噪后的信号。

1.3 IMF分量的小波阈值降噪方法

针对含噪分量Ij(j=1,2,…,y)实施小波阈值降噪。其中，阈值处理部分直接决定了降噪效果的好坏，目前阈值量化规则主要是软阈值函数和硬阈值函数两种，软阈值函数会过量的压缩信号使其失真但信号连续性好，硬阈值函数会较好的保留信号但是存在不连续问题。现有解决方法大多是王亚萍等研究的半软阈值，即

η(ω，T1，T2)=

(5)

式中:ω为小波系数；T1，T2为两个阈值，改变两个阈值可以实现上述要求但是需要调整两个参数，操作麻烦。石大磊等的研究令T2=1.16T1，完善了上述问题。

在阈值降噪过程中，阈值函数处理的是各层的小波系数，尺度系数几乎是有用成分故不做处理。

小波系数由噪声成分与有用成分组成，且每个含噪分量Ij(j=1,2,…,y)的小波系数含噪情况不一。因此希望对噪声成分较多的含噪分量Ij(j=1,2,…,y)采用偏软的阈值函数，尽可能实现对噪声成分的压缩；对有用成分较多的含噪分量Ij(j=1,2,…,y)采用偏硬的阈值函数，从而尽可能的保全有用成分。文献[10]引入可以调参的阈值函数，调参参数取值范围在0～1，可以使得阈值函数在软阈值和硬阈值之间转变。但是本次降噪的含噪分量有用成分占大部分，如果阈值函数特别接近软阈值时，会使得降噪后的信号精度偏差比较大，因此本文构造可调参的连续阈值函数，即

η(ω，λ，s)=

(6)

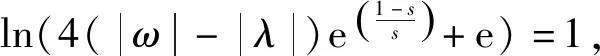
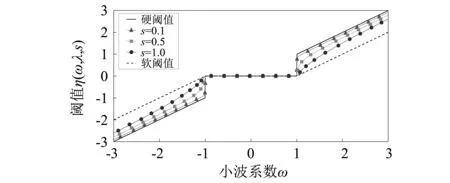
图1 新阈值函数Fig.1 New threshold function

1.4 样本熵改进的CEEMD与自适小波阈值组合降噪步骤

原始信号经过CEEMD分解成若干个不同频率特性的IMF分量，由于不同的原始信号含噪程度不同，所以其每个IMF分量含噪情况也不同，因此结合样本熵筛选出噪声分量、含噪分量和信号分量。含噪分量内噪声与有用信号混杂需对其进行小波降噪处理。为自适应的提高其降噪效果，用样本熵值表征其含噪程度与上述构造的自适应阈值函数相结合，使得每个含噪分量的阈值函数取决于分量本身含噪程度。结合样本熵改进阈值量化规则具体步骤如下。

步骤1直接去除噪声分量Ii(i=1,2,…,x)。

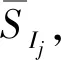
步骤3对含噪分量Ij(j=1,2,…,y)进行改进的小波阈值降噪，选用本文的提出的阈值函数，并且含噪分量Ij(j=1,2,…,y)对应的阈值函数的调参参数为sj(j=1,2,…,y)。

步骤4将降噪后的含噪分量与信号分量重构成降噪后的信号。

2 仿真验证

本文搭建OPAX模型使用的是发动机加速工况下的振动信号，该信号含噪需要进行降噪处理，为了模仿此类工况数据信号采用调幅调频信号s(t)为原始不含噪信号，具体如图2所示。仿真信号f(t)

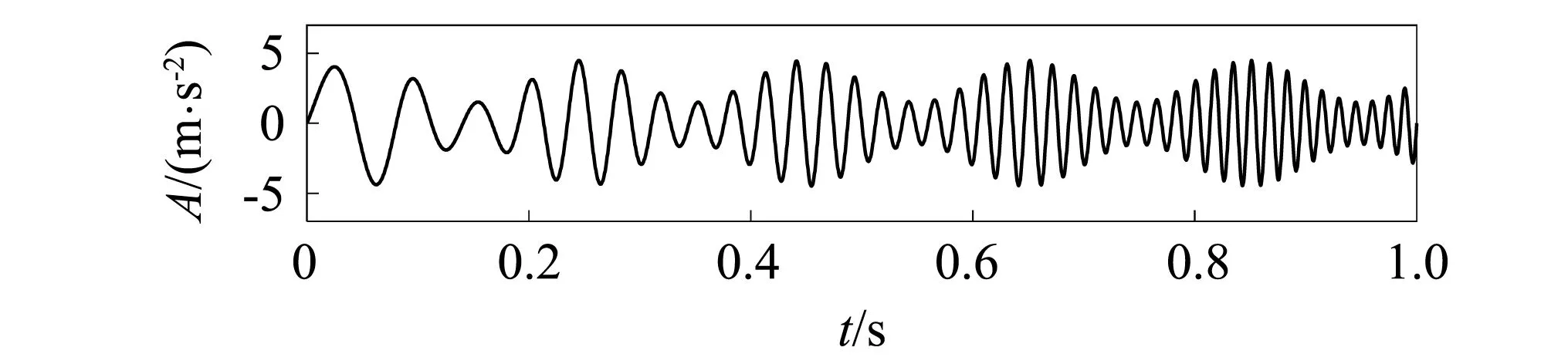
图2 原始信号s(t)Fig.2 Original signal s(t)

(7)

式中:t∈[0,1],采样点为3 000个；加入的噪声信号n(t)功率是s(t)的0.2倍，得到的仿真信号f(t)，如图3所示。

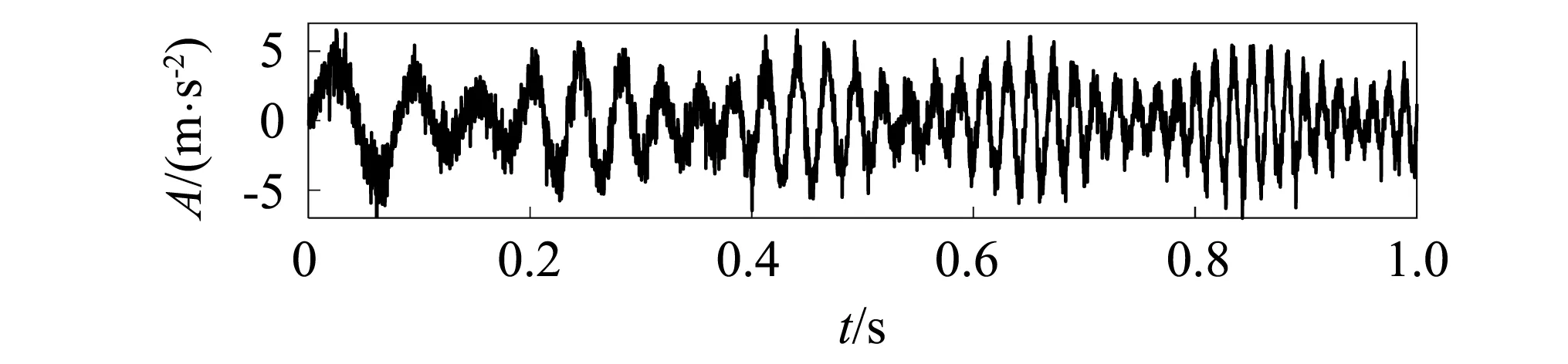
图3 仿真信号f(t)Fig.3 Simulation signal f(t)

将仿真信号f(t)做CEEMD分解得到如下7个IMF分量以及一个余项r(t)，如图4所示。

式中:ψ(x,xk)是核函数，目的是从分解信号抽取特征，将分解信号中的样本映射为高维特征空间中的一个向量，以解决原始分解信号中线性不可分的问题。

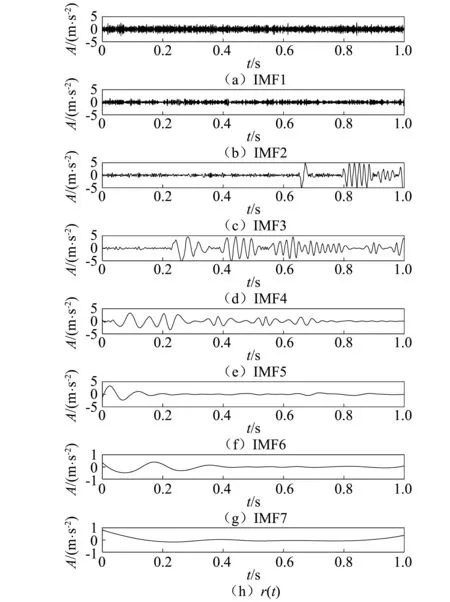
图4 CEEMD后各个分量Fig.4 The components after CEEMD

运用CEEMD与软阈值函数的小波降噪、CEEMD与硬阈值函数的小波降噪、王亚萍等和石大磊等的研究方法以及本文方法做降噪处理，本文方法根据1.4节的降噪步骤挑选并去除噪声区间、对含噪区间进行样本熵改进的小波阈值降噪然后和信号区间一起重构，具体流程如图5所示。

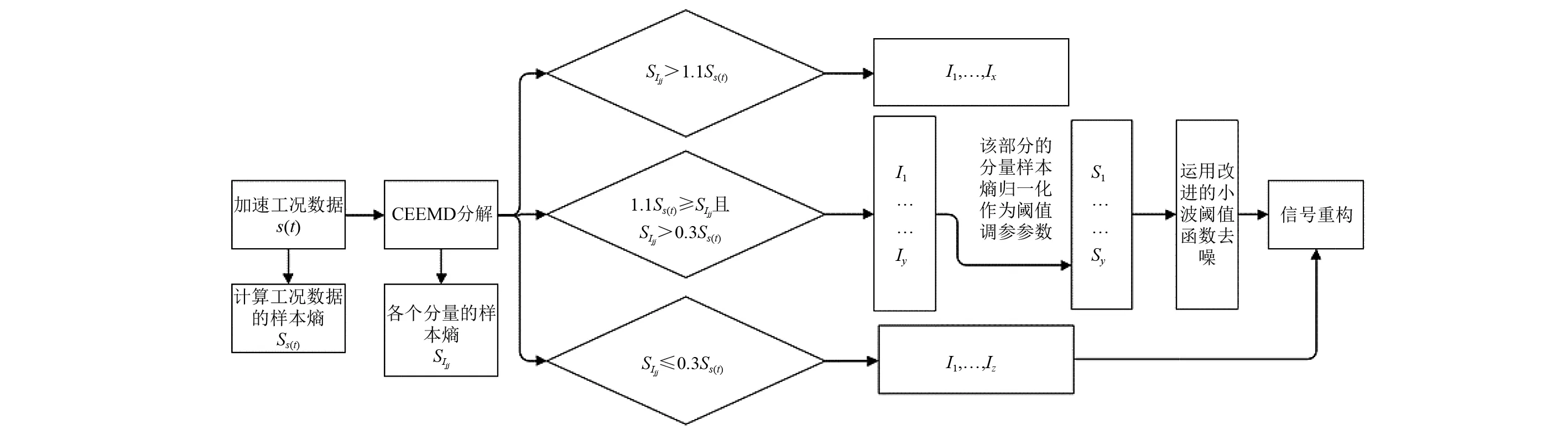
图5 本文去噪流程图Fig.5 Denoising flowchart of this article

如图6为上述5种方法降噪后的效果，其中图6(a)以及图6(b)是传统的CEEMD与小波组合降噪后的效果，采用小波软硬阈值对含噪区间。

重构后信号较仿真信号来说，其信号噪声含量有所减少，但较原始信号来说仍然存在差异，效果不佳。王亚萍等和石大磊等的研究方法以及本文方法分别采用半软阈值函数、改进的半软阈值函数以及样本熵改进的自适应阈值进行的降噪处理函数，如图6(c)、图6(d)以及图6(e)所示，降噪后的信号接近仿真信号。

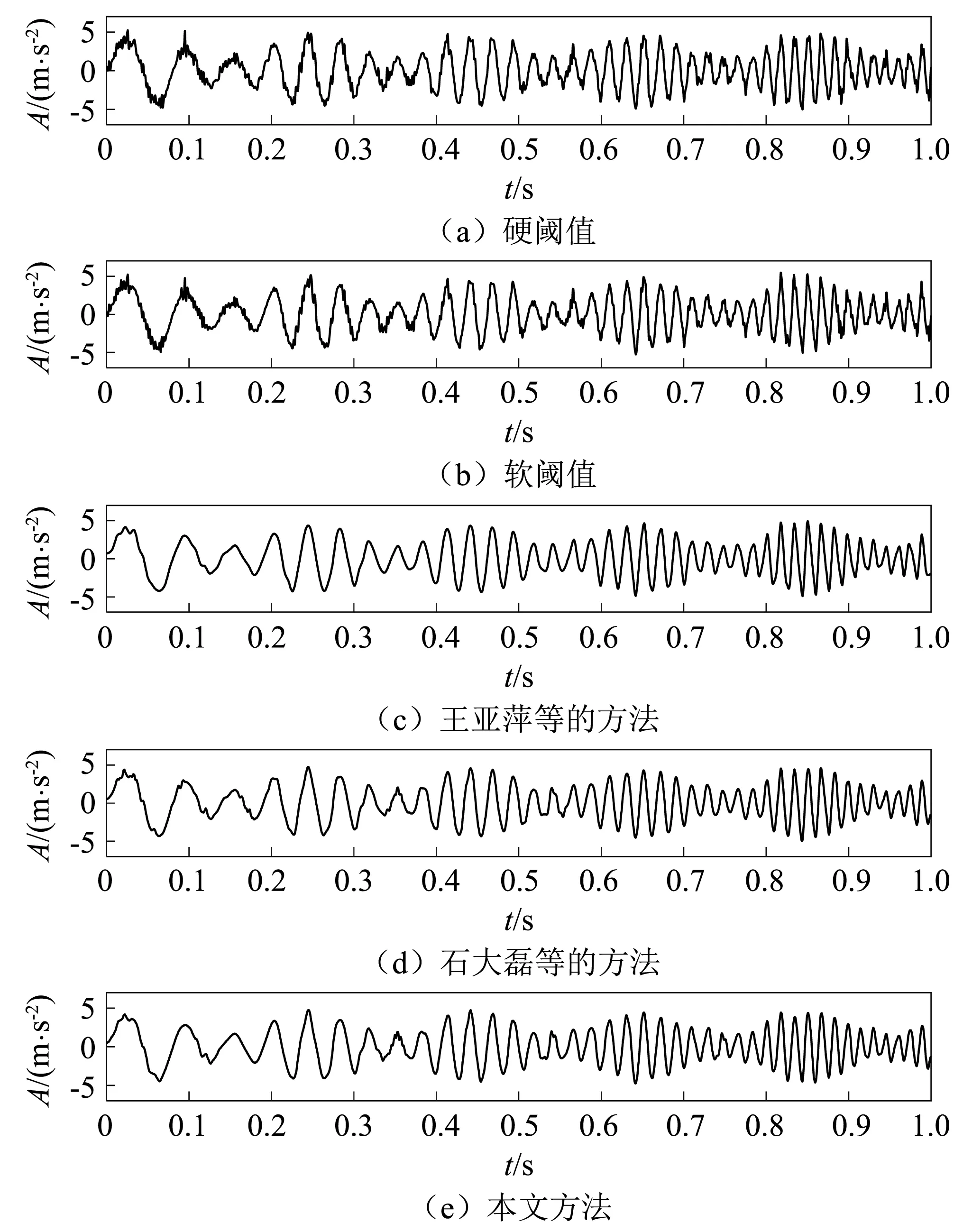
图6 5种阈值降噪方法对比Fig.6 Comparison of five threshold noise reduction methods

为了更好的验证降噪效果，可以从降噪后的信号与原始信号的相近程度来说明问题。应用降噪后的信号和原始信号的均方根误差(root mean squared error，RMSE)与信噪比(signal noise ratio，SNR)判断降噪效果。RMSE越小，说明降噪后的信号与原始信号越相似；SNR越大，说明降噪效果越好[11]。在处理庞大的振动信号工作中，算法计算时间直接关乎到效率，因此对上述几种方法的算法时间做出统计。

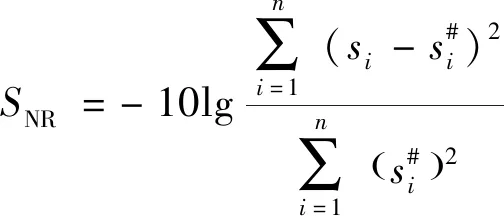
(8)

(9)

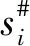
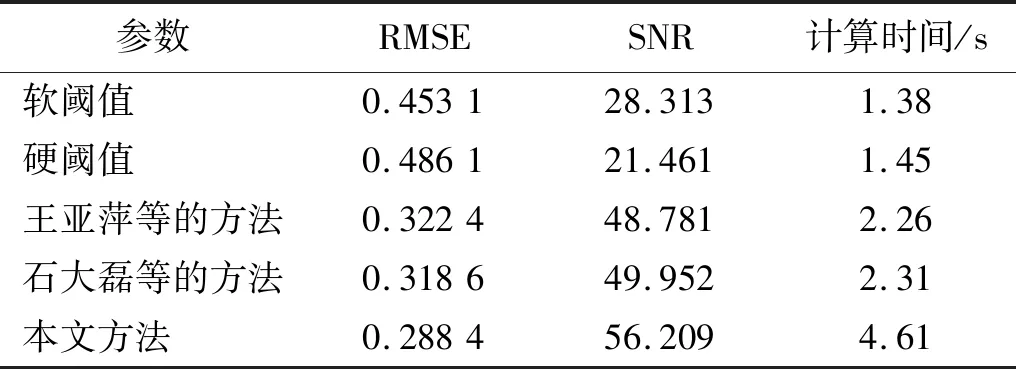
表1 不同方法的降噪后的效果对比Tab.1 Comparison of the effects of different methods after noise reduction

3 OPAX方法模型验证

OPAX 方法从结构的角度出发，具体到某个目标点的振动总量可表达如式(8)[12]所示

(10)

式中:Y(ω)为目标点的总的振动响应量;Hp(ω)为频响函数;n为传递路径个数;ω为固有圆频率;Fp(ω)为路径输入点载荷;p为传递路径序号。本次试验中，频响函数是通过锤击法得到的，对路径输入点载荷来说则需要悬置主被动端的加速度进行载荷识别，即

(11)

式中:Kp(ω)为悬置动刚度;aep(ω)为发动机主动端的振动信号;abp(ω)为发动机被动端的振动信号。

试验样车是国产某型SUV，别在发动机3个悬置的主被动端、座椅滑轨以及转向盘和车底板加装加速度传感器，具体如图7所示。在汽车空挡期间，运用LMS Test Lab数采前端，采集汽车发动机转速在1 200～4 000 r/min的静置匀加速工况数据，即汽车在此加速工况下上述所有点的时域振动加速度振动信号。在汽车熄火期间运用锤击法获得频响函数，要求测试的相干系数都大于0.9，从而保证频响函数结果的可靠性。

图7 传感器布置Fig.7 Sensor arrangement

OPAX模型的搭建过程：先应用测得的工况数据根据式(10)以及式(11)进行载荷识别，得到悬置动刚度Kp(ω)；再运用式(11)进行载荷Fp(ω)的识别；最后如式(10)所示，结合频响函数得到路径振动贡献量的计算值

(12)

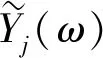
为了更进一步的提高降噪效果，对于含噪不同的含噪分量，本文提出一种新的小波阈值函数并结合样本熵对其给予自适应的阈值量化规则。图8为采集的发动机转速在1 200～4 000 r/min的匀加速右悬置被动端X方向工况数据以及本文方法降噪对其后的结果，可以看出信号大部分毛刺被剔除，初步表面本文降噪方法有效，且噪声信号特征为中高频率低幅值，车身共振频率为低频段，故而不会滤除共振频率。为了进一步证明改进后的效果，分别应用原方法、现有的4种CEEMD与小波阈值组合降噪方法和本文方法对工况数据进行降噪，降噪后将各自工况数据用于搭建各自的OPAX模型。

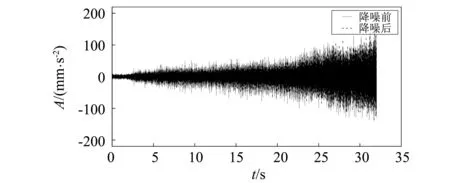
图8 右悬置被动端X方向工况数据Fig.8 X-direction operating data of the passive end of the right suspension

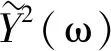
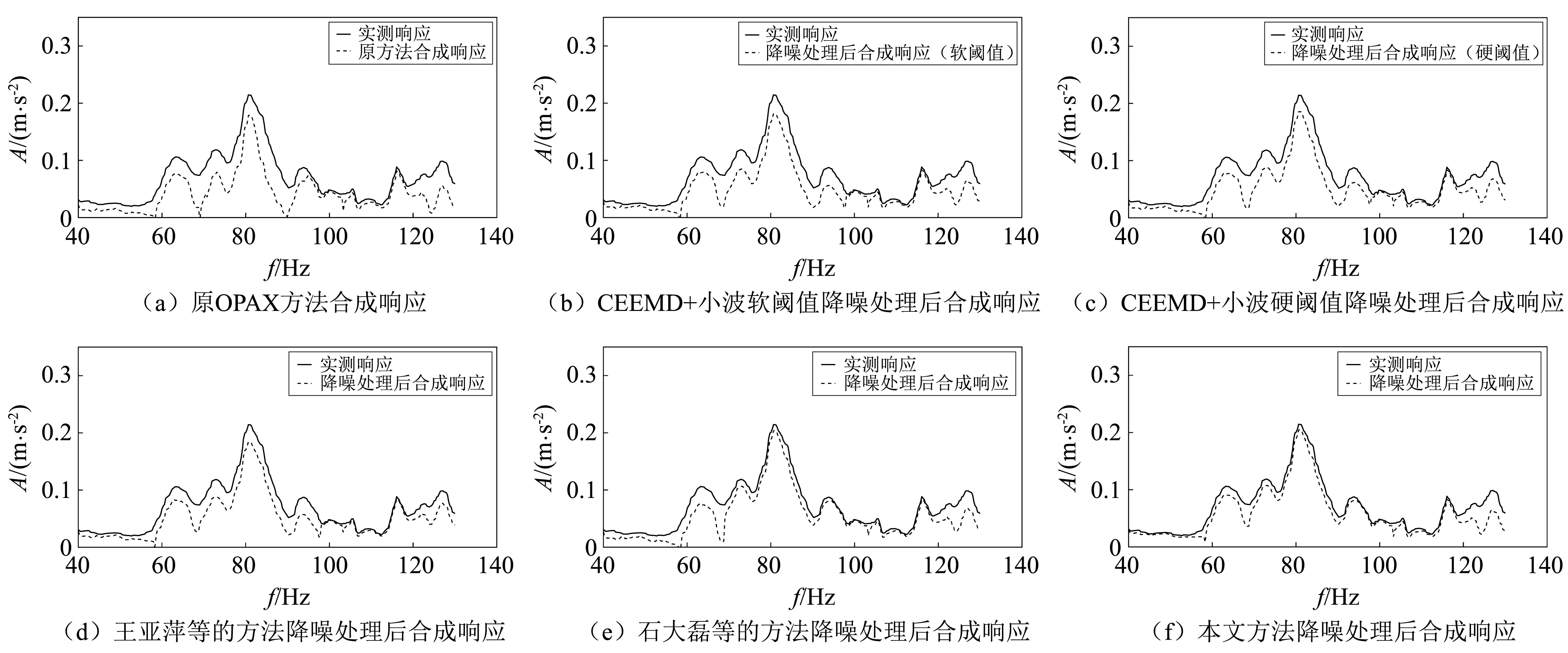
图9 座椅滑轨Z向2阶合成响应与实测响应对比Fig.9 Comparison of Z-direction 2nd order synthetic response and measured response of seat rail

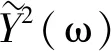
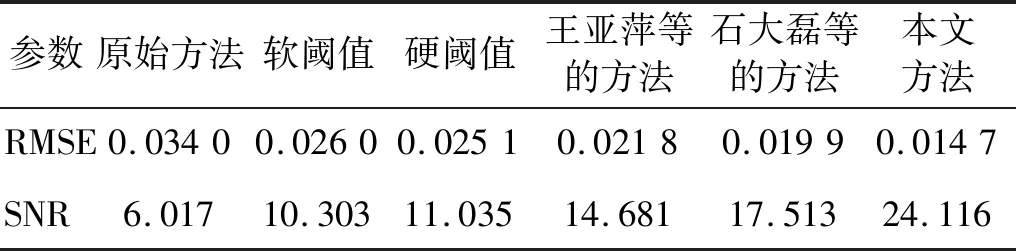
表2 合成响应与实测响应之间的SNR与RMSETab.2 SNR and RMSE between synthetic response and measured response

应用4种CEEMD与小波组合降噪方法和本文方法都提高了OPAX模型的精度，其中本文方法结合样本熵对含噪不同的含噪区间给予更适合的阈值函数，提高了自适应性同时也使得目标点的合成响应更加接近实测响应。如图8所示，较其他方法整体与实测响应较为接近，尤其在82 Hz左右的峰值处以及低频处其本文方法效果最为明显。且目标点的合成响应与实测响应RMSE与SNR分别是0.147和24.116，均优于其他方法。但是在68 Hz以及120～130 Hz左右存在较大的误差，可能测量过程中的误差因素以及遗漏了吊耳与轮胎等处的路径从而造成的。

4 结 论

为提高OPAX模型计算精度，提出了基于CEEMD与自适小波阈值组合降噪方法处理OPAX模型庞大且复杂的工况数据，并有以下特点：

(1)将样本熵作为评判CEEMD分量的标准，并划分为直接剔除的噪声分量、小波降噪处理的含噪分量以及直接重构的信号分量。

(2)含噪分量中每个分量的小波系数含噪量是不同的，应用样本熵归一化后的参数作为表征参数。配合本文创建的阈值函数实现对含噪较高分量的小波系数进行大尺度的压缩，而对含噪较低分量的小波系数则尽可能的保护，提高阈值自适应性的同时也提高了降噪效果。

(3)应用到OPAX模型中即对其工况数据(振动信号)进行降噪。与同类方法对比，通过仿真分析发现本文方法与原始信号接近程度较高；通过OPAX试验验证发现降噪处理过的模型得到的目标点的合成响应更加接近实测响应，且通过RMSE以及SNR对比验证发现本文方法降噪处理后搭建的OPAX模型目标点的合成响应与实测响应一致性最高，因此本文方法搭建的OPAX模型分析精度提升效果最佳。