超静定转子系统不对中动力学的理论与实验研究
2021-09-27王亭月李盛翔李方忠马文生
赵 广,王亭月,李盛翔,李方忠,马文生
(1.大连理工大学 能源与动力学院,辽宁 大连 116024;2.中国航发四川燃气涡轮研究院,四川 绵阳 621000;3.重庆水泵厂有限责任公司,重庆 400033)
现代航空发动机低压转子系统由于跨度大常采用套齿连接风扇和涡轮转子,且套齿两端常采用圆柱定位面实现径向定位,低压转子一般采用3个弹性支撑,使其具备典型的超静定转子的结构特点。由于制造与装配误差,热变形与结构变形,使得发动机转子系统的支撑不对中广泛存在。不对中会引起超静定转子系统出现临界转速漂移、振幅加剧、振动频率复杂等非线性振动现象。
许多学者中通过理论方法得到轴的外力和力矩,分析轴的变形与受力之间的关系情况来模拟轴的不对中[1]。Gibbons[2]对转子系统不对中的研究是最早的。Sekhar等[3-6]建立了含联轴器及轴承的不对中系统理论模型,分析了含裂纹转子的临界力学状态。Dewell等[7]通过理论推导,得知检测2X和4X分量可以对含联轴器的转子系统进行不对中诊断的手段。Xu等[8]通过理论和实验分析了含柔性联轴器不对中转子系统。徐梅鹏等[9]根据航空发动机双转子的结构特点,将外转子支点不同心的影响转化为支承上的等效不同心弯矩,并通过力矩分解处理得到系统的振动方程,结果表明:外转子支点不同心使系统的幅频响应产生新的共振区,在该共振区内系统的振动响应中包含2X频成分。
在超静定转子方面,Feng等[10-11]在理论上进行了深入的工作,发现不对中量和轴承种类对系统的固有频率及不平衡响应都有影响,其中对轴承稳定性影响比较大的是轴承剖面及其上的反应载荷;间隙形状的变化和横向不对中均会改变动、静态系数进而影响系统的动态特性;在不对中情况下,椭圆轴承也比圆轴承的运行稳定性更好。在上述研究基础上,Hu等[12-13]针对超静定转子系统,仿真计算得到固有频率、振型,并对稳定性进行了研究,预测了不对中变化量对系统振动特性的影响。刘永泉等[14]针对航空发动机三支点柔性转子系统的支承不同心问题建立了不同心激励下多跨度柔性转子系统的力学模型,结果表明支承不同心不仅引起转子过渡轴的刚度非线性,而且会产生2X频激励。
综上所述,国内外针对超静定转子开展其不对中振动特性的研究很少,以定性研究为主,且不对中激励模型仅考虑某单一因素的影响,缺乏系统的理论建模和实验检验。本文利用D’Alembert原理建立了考虑弹性支承和不对中的超静定转子动力学解析模型。通过去除尾部支点位置处的多余约束,理论换算了不对中的动态附加激励力,以及对系统刚度矩阵的影响,通过计算获得超静定转子系统的固有特性和振动响应,最后,进行了实验研究,验证了不对中超静定转子系统的振动规律。
1 尾部支点不对中激励建模
典型超静定转子系统的力学分析模型示意图,如图1所示。包括3个弹性支撑、2个集中质量轮盘。转子的套齿连接结构位于2#支点位置所在轴段。
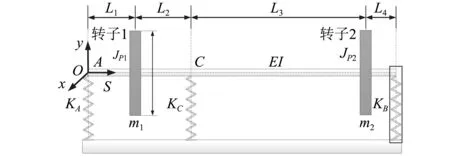
图1 超静定转子力学分析模型示意图Fig.1 Mechanical analysis model of statically indeterminate rotor system
假设不对中发生在尾部支点垂直方向(上图方框位置),当尾部支点抬高ΔY时,在转子系统的支点处会产生使其抬高的力FY,中间支撑位置处亦会产生弯矩MY;图2中,将FY方向转子的沿x方向的变形为ΔX,Δb为支承变形。以尾部支点做分析点,画受力分析图,由变形是协调一致及力和力矩平衡方程,可得到FY和MY。
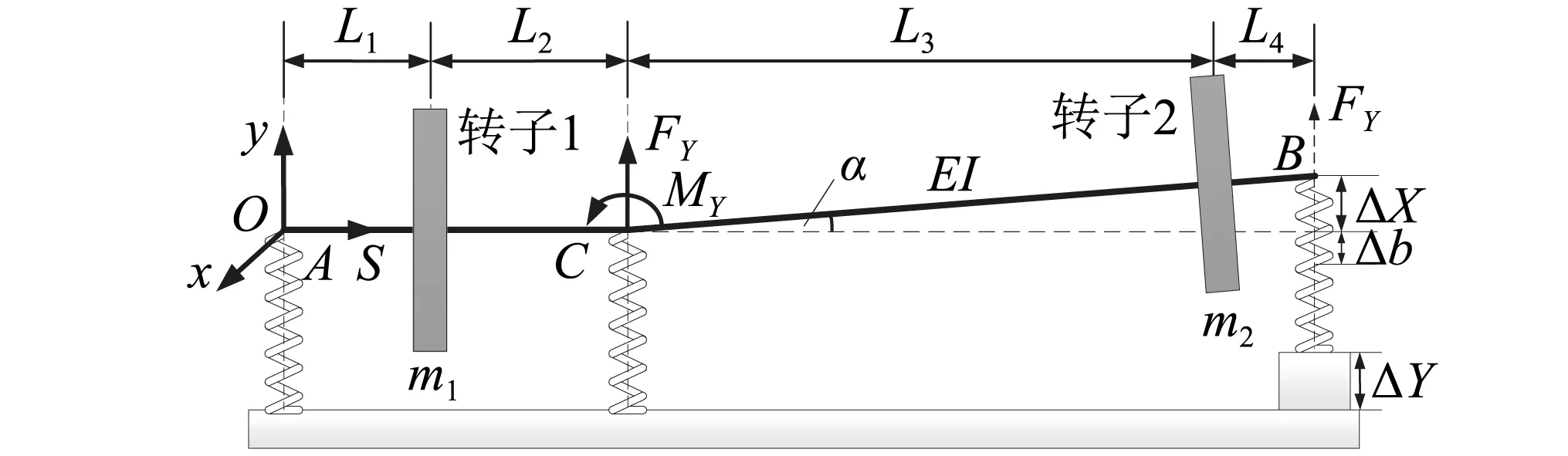
图2 尾支点不对中示意图Fig.2 Schematic of tail support misalignment
(1)
MY=dFYcosα
(2)
1.1 尾支点不对中附加激励推导
套齿连接结构,如图3所示。转子1、套齿轴和转子2的相对运动关系,如图4所示。转子1和转子2投影在与套齿轴垂直的平面上。转子1的横截面是圆,转子2的横截面是椭圆。转子1、转子2分别绕O1和O2转动,O′为结构集合中心点,与O1,O2不在同一个位置,并具有相对位移,套齿联接结构转动的中心点为P,Δe为O1和O2的间距(Δe=ΔLtanα,ΔL为该结构轴向尺寸,α为两转子间不对中角度)。
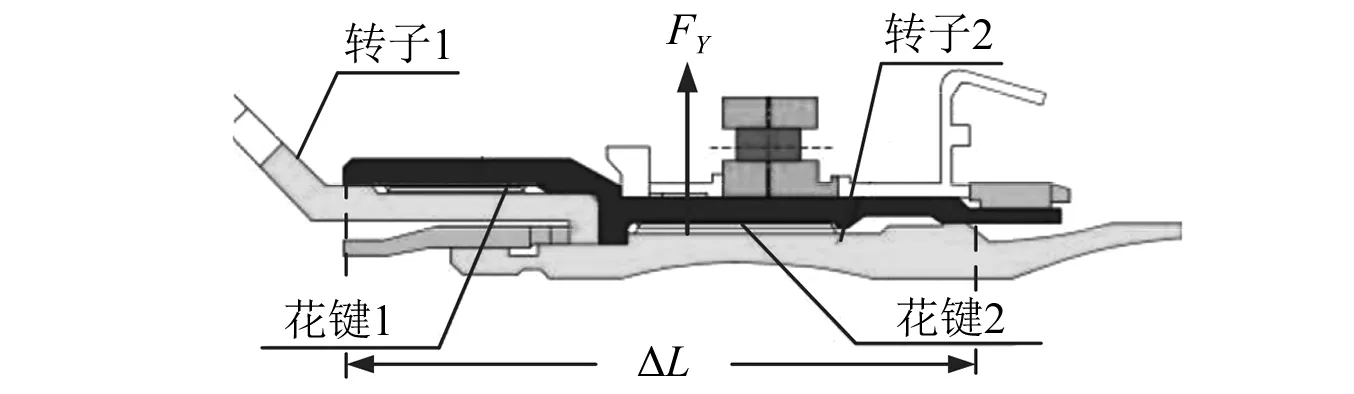
图3 套齿连接结构Fig.3 The structure of spline join
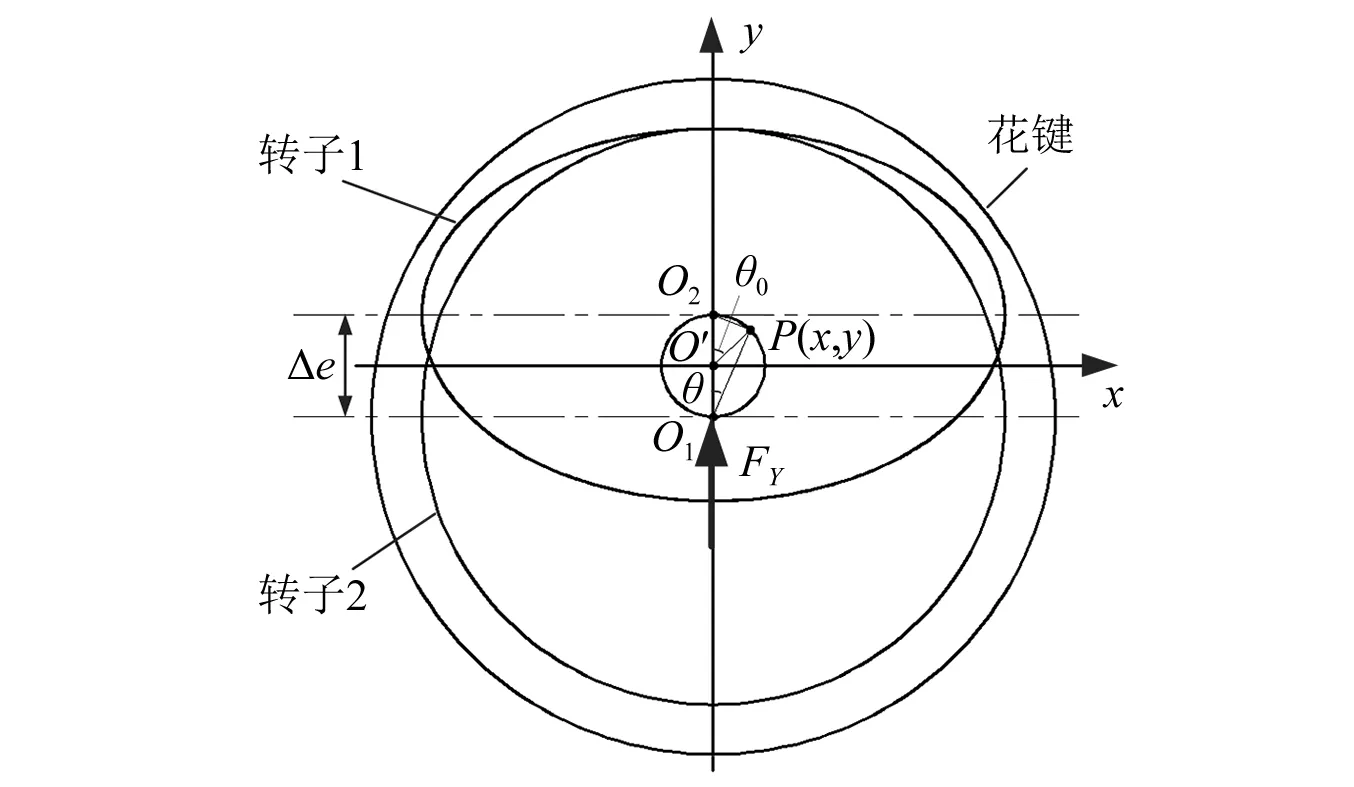
图4 转子间相对运动轨迹图Fig.4 Relative motion of two rotors
在整个系统旋转的过程中,由于尾支点存在偏移,中间支承出现角度偏差α。套齿连接结构以O′为圆心做空间公转,Δe为公转直径,θ为自变量,P(x,y)为点P位置,ω为旋转速度,忽略扭转变形,P点位置可以表示为
(3)
对时间t的求导
(4)
点P角速度
(5)
分析可得动态中心点P绕回转中心角速度为基频的2倍。点P的运动过程实质上等同于质量不平衡系统的离心力引起的径向振动。
式(5)对时间t求导。
(6)
静态不对中力FY和作用在套齿联接结构上的附加激励,共同组成了动态附加激励Fδ,两方向分量为
(7)
式中:θ0=2θ=2ωt;mc为套齿连接结构质量。
代入式(7),Fδ可以写成
(8)
1.2 传递扭矩导致的附加激励
2个转子间传递扭矩的过程,如图5所示。图中os方向为转子1回转方向,oz方向为转子2回转方向,由于不对中导致的两转子夹角为α,转子1为主动转子,转子2为从动转子,转矩T通过套齿连接结构传递。可分为两部分T1,T2:轴向转矩T1=Tcosα,使转子扭转;径向转矩T2=Tsinα,使转子弯曲。
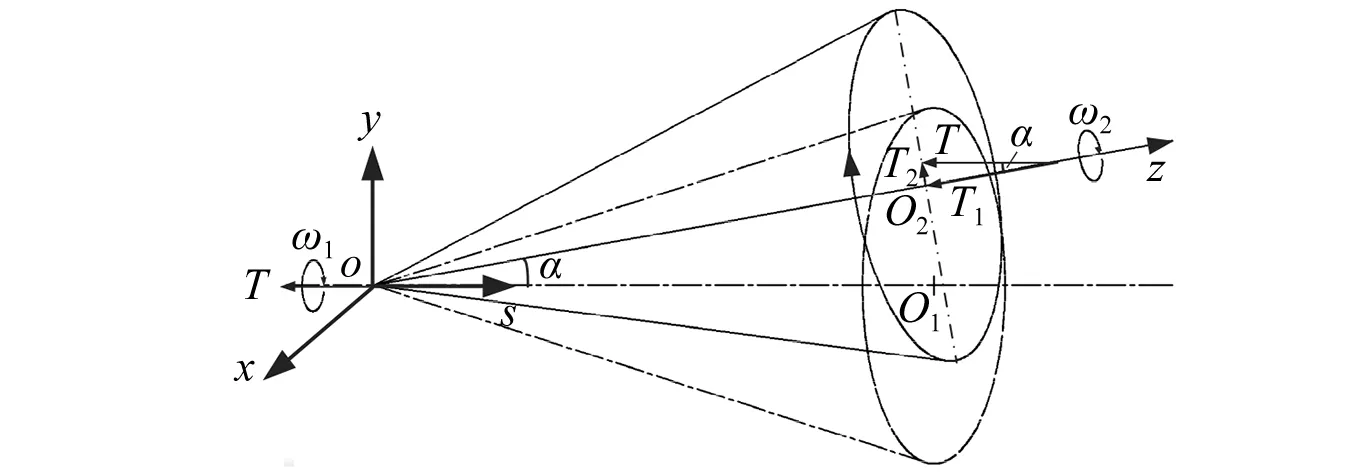
图5 扭矩传递示意图Fig.5 Torque transmission diagram
由于转子仅绕轴线旋转,oz方向的转矩为
Tcosα=Jsβ2
(9)
式中:Js为系统转动惯量;β2为转子2角加速度。当转子1旋转时,转子2旋转转速ω2其从动于ω1。中间联轴器角度不对中产生的两侧转子角度变化情况,如图6所示。转子1、转子2角度变化情况如图7、图8所示。根据力矩平衡,中间支点两侧的扭矩相等。当两侧转子各绕轴转动一周时,圆C与圆D分别为转子1上点A及转子2上点B的轨迹。θ1为转子1转动角度,θ2为转子2转动角度,在垂直于轴线的平面上,对左右两侧转子的转角投影,而两轴啮合圆半径相同,本文用r表示。两转子的初始位置OA0及OB0看作2个向量。
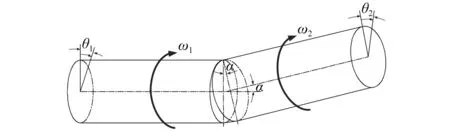
图6 转角不对中关系图Fig.6 Sketch of angular misalignment
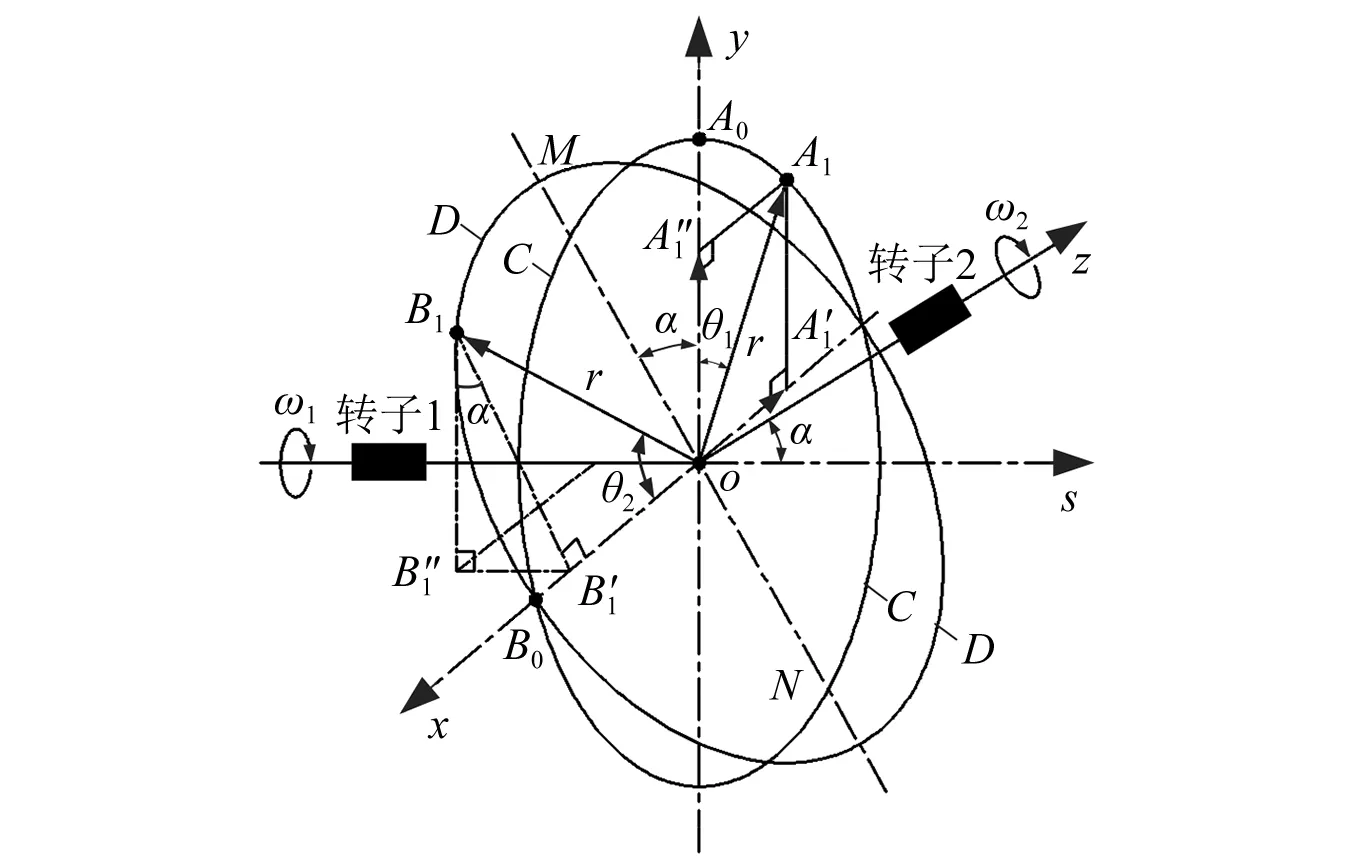
图7 不对中角度变换Fig.7 Misalignment angular transformation
在转子1转过θ1后,A0到了A1的位置,OA1为OA0的新位置,因圆C⊥os轴,OA1在s轴上没有分量,在x轴上:OA′1=-rsinθ1。在y轴上:OA″1=rcosθ1。
类似的,向量OB1可表示为
OA垂直于OB,点积等于零。
OA1·OB1=(OA1)T(OB1)=
(10)
展开式(10)可得
r2cosθ1sinθ2cosα-r2sinθ1cosθ2=0,
tanθ1=tanθ2cosα
(11)
等式(11)的两边同时对时间t求导
(12)
等号两边平方得tan2θ1=tan2θ2·cos2α,代入式(12),再利用倍角公式得到
(13)
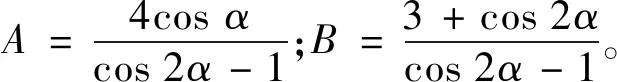
用广义二项式定理进行展开,并利用倍角公式降次,再对两边求导得到
(14)
式中:β2为从动轴角加速度;设θ1=ω1t,因此可得到转轴的扭矩表达式
(15)
根据转矩、阶数的定义,当尾部支点失调时转矩传递引起的动态外激励可以改写为
(16)
Fs与轴径Rs,不对中偏角α,主动轴绕轴转动的角速度ω1等参数有关。因为高频幅值小于低频幅值,保留前4阶后
Fs={P1}sin 2ω1t+{P2}sin 4ω1t+
{P3}sin 6ω1t+{P4}sin 8ω1t
(17)
2 超静定转子系统不对中动力学建模
当尾支点产生不对中时,整体变形如图8所示。由受力平衡,计算得到点A和点B的支反力及其上的支承变形,再根据几何关系,得到FY单独作用下时弹性支承的变形情况
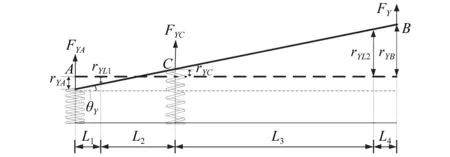
图8 FY作用下的支承变形Fig.8 Deformation under FY
(18)
式中,在FY单独作用下,系统产生角度变化为θY,转轴变形为rYL1,rYL2及rYB。
在尾支点不对中的情况下,静态综合变形如图9所示,左右两轮盘产生的变形分别为
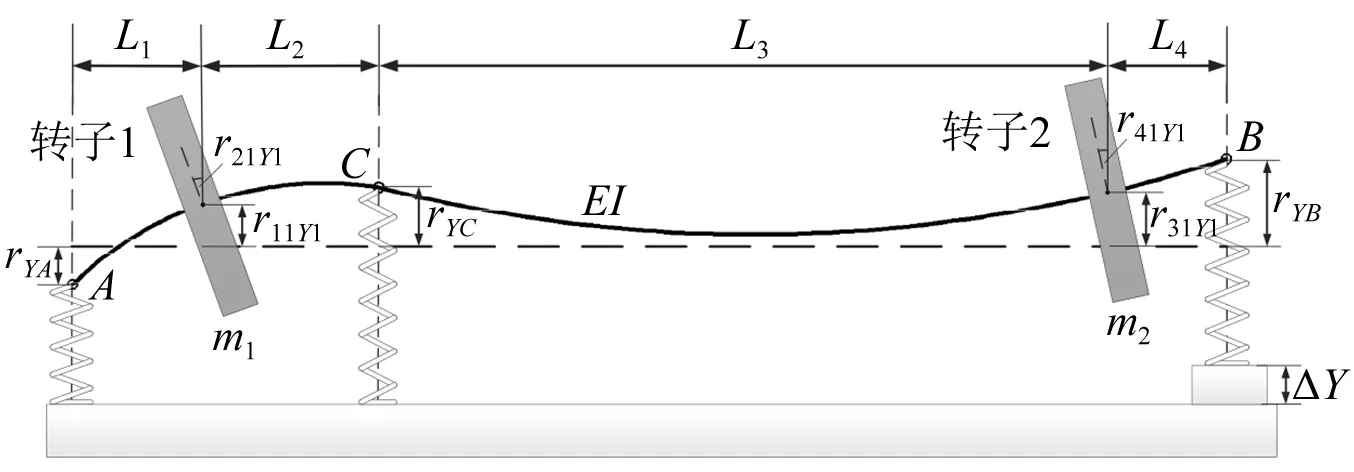
图9 尾支点不对中综合变形Fig.9 Comprehensive deformation with tail support misalignment
(19)
不对中修正系数为
(20)
由于存在尾部支点不对中,需要考虑其对动态附加激励的影响,进而产生的对柔度矩阵的影响,对柔度矩阵进行相应的处理,进而可得尾部支点不对中时,系统的柔度矩阵[Rm]及其刚度矩阵。
选择{u}=[y1θx1y2θx2x1θy1x2θy2]T作为广义坐标,用D’Alembert原理可以写出不对中超静定转子系统运动微分方程。
式中:[M],[G]和 [Km]分别为不对中状态下的质量矩阵、陀螺矩阵和刚度矩阵。Q(t)为外力矢量,包括3个部分
Q(t)=Fe+Fδ+Fs
(21)
式中,φ为系统初始相位角。
3 不对中动力学特性计算与分析
当转速Ω=40 Hz,偏心距e1=e2=10 μm,尾支点不对中ΔY=200 μm,初始相位φ=30°时,转子2响应的时域图、频域图及转子轴心轨迹分别如图10~图12所示。可以发现:由于尾支点不对中,导致转子2轮盘1X振动增加到40.1 μm,同时新的2X响应分量出现,振幅为60 μm,轴心轨迹呈内‘8’字形。
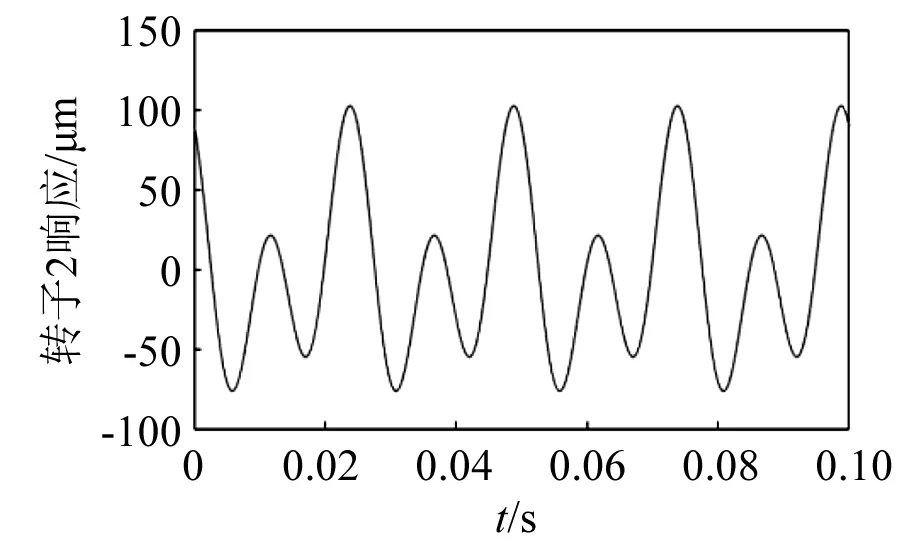
图10 时域图Fig.10 Time domain response
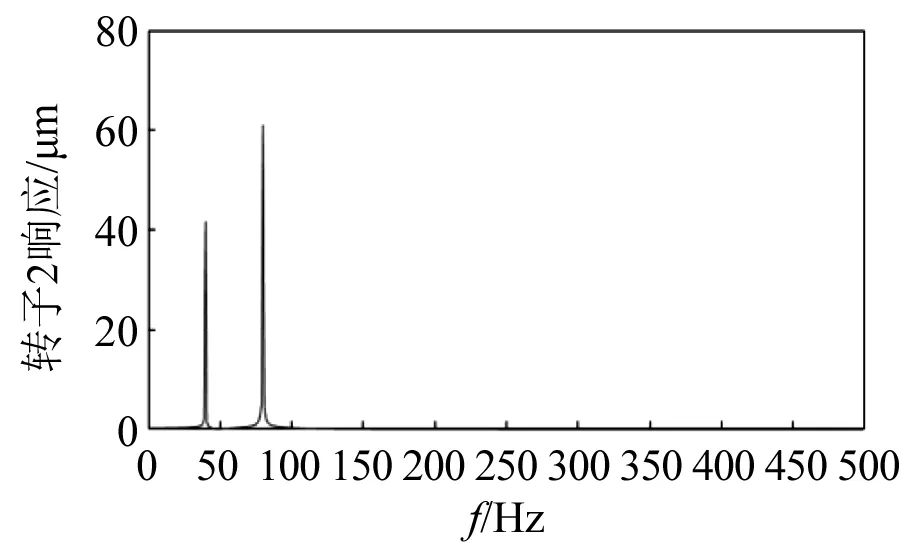
图11 频域图Fig.11 Frequency domain response
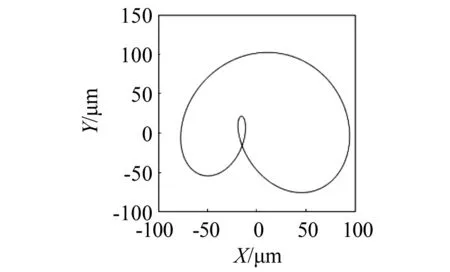
图12 轴心轨迹Fig.12 Axis locus
当转速不变时,转子1、转子2轮盘的轴心轨迹随不对中量的变化,如图13和图14所示。结果表明:不对中量越大,轴心逐渐从椭圆形变为内“8”字形。
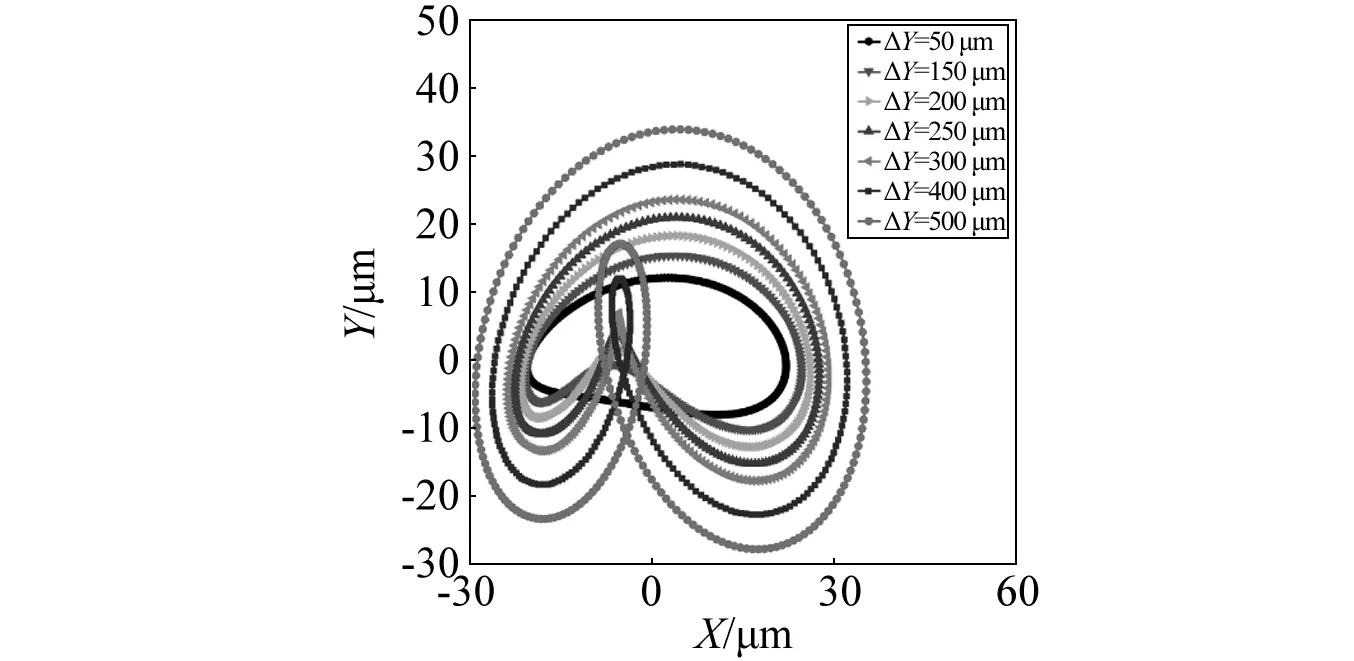
图13 转子1轮盘轴心轨迹Fig.13 Orbits of rotor 1
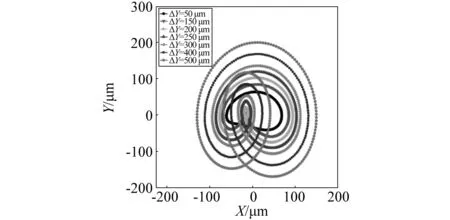
图14 转子2轮盘轴心轨迹Fig.14 Orbits of rotor 2
转子2水平方向,振动响应随不对中变化的时域图,如图15所示。图15表明:随着不对中量ΔY的增加,系统振动响应的水平向1X分量变化不大,2X分量变化更快,因此,可以看出转子2后支点不对中越严重,2X分量所占比例越高。
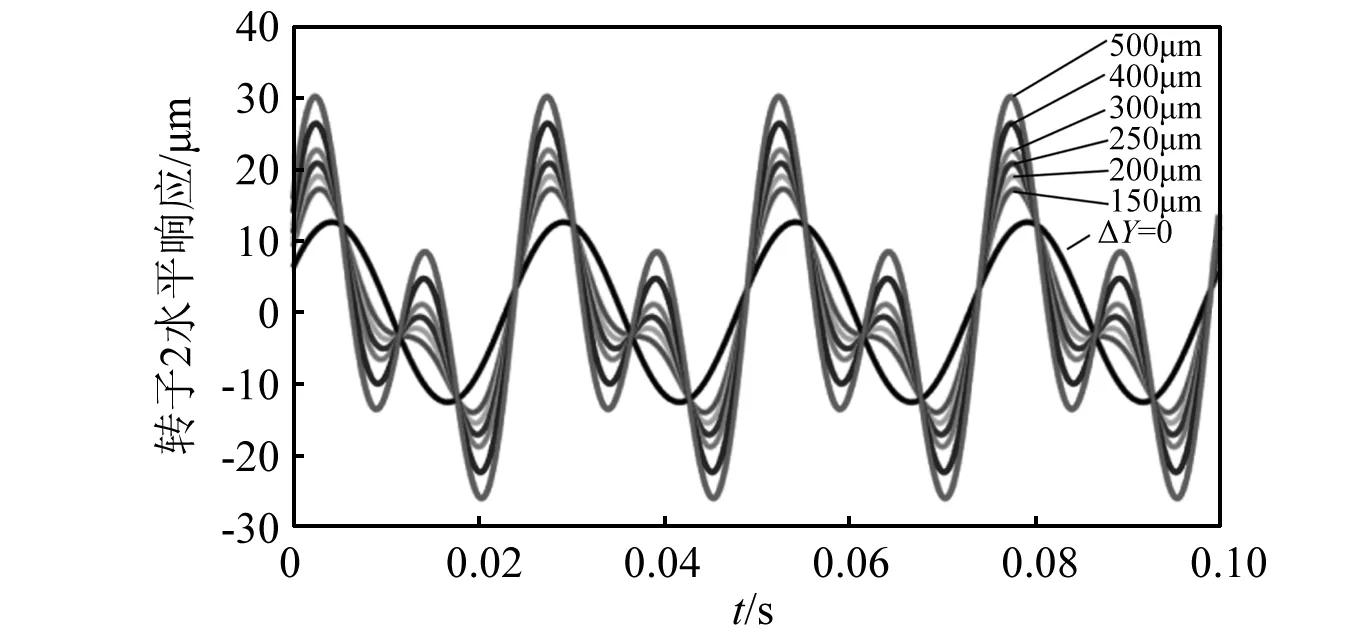
图15 转子2水平向振动响应Fig.15 Vibration response of rotor 2 in horizontal direction
固定不平衡状态,转速为2 400 r/min,不对中量在0~300 μm调整,轮盘的振幅,如图16和图17所示。随着不对中量的增长,2个转子水平向1X分量只有很小的变化,2X分量增大且线性;从图17可知:对于竖直向,两轮盘的1X分量总体稳定;而垂直向的2X分量随不对中增大,在100 μm位置出现突变,之后振幅增大更加显著。当整个系统中存在转子2后支点不对中时,频谱图将会出现1X和2X响应分量,并随着不对中量增大而增大;2X增加量较1X更大,比例亦更高。
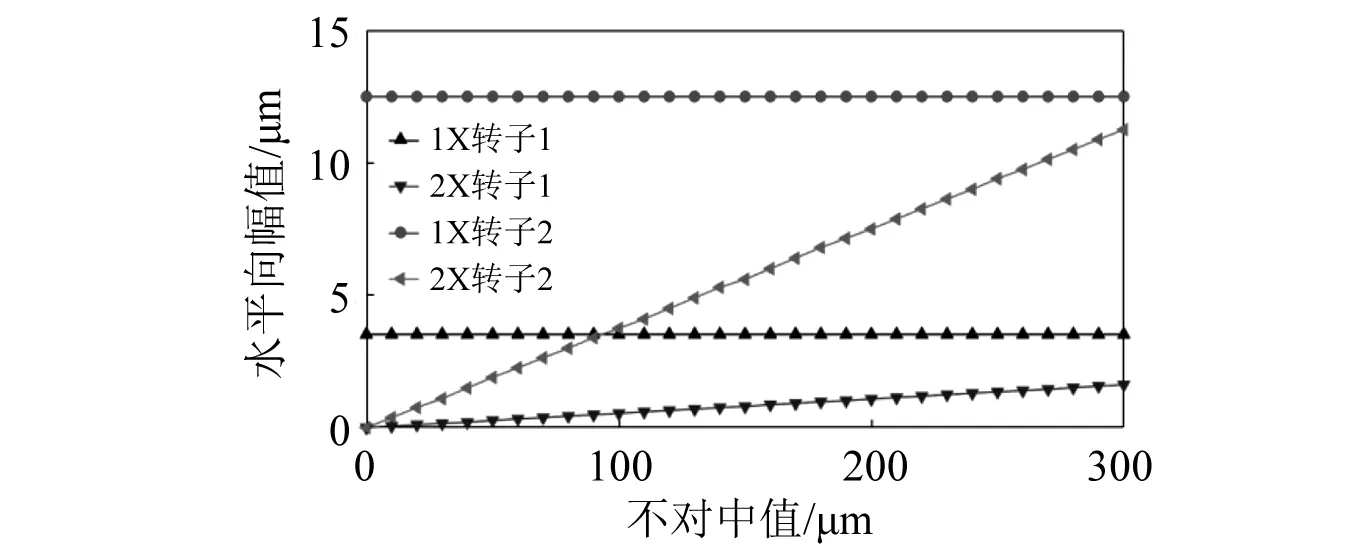
图16 水平方向1X和2X响应Fig.16 1X and 2X response in horizontal direction
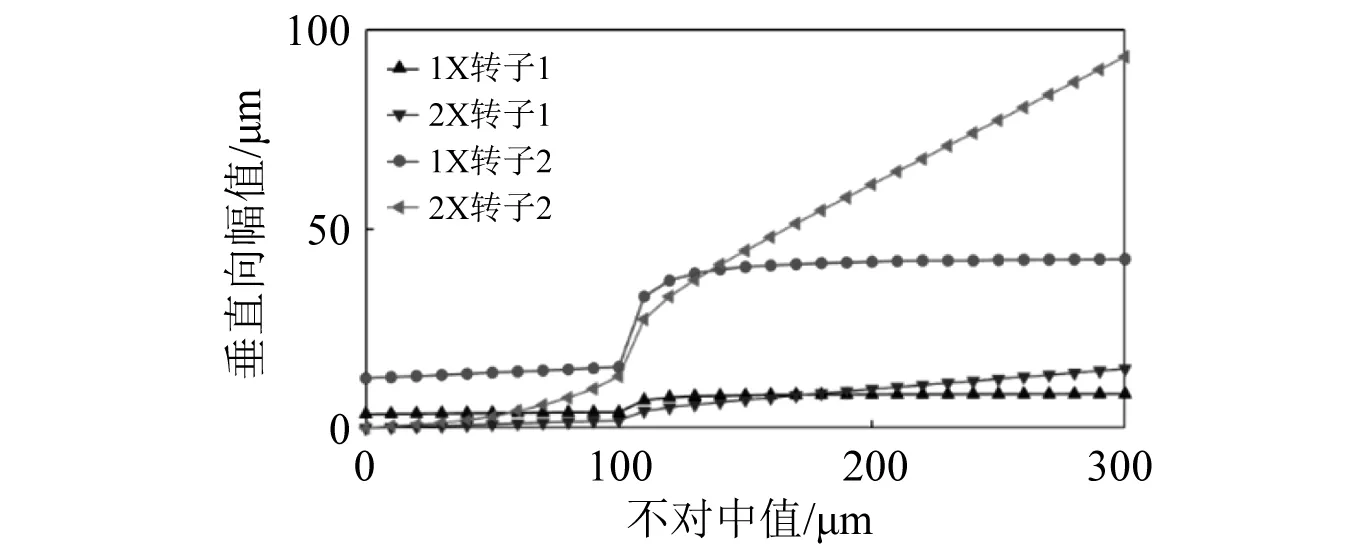
图17 垂直方向1X和2X响应Fig.17 1X and 2X response in vertical direction
这是由于轮盘两端间距大,轮盘安装并不对称,不对中在尾部出现,轮盘初始位置发生改变,不平衡偏心出现,故相比于转子1轮盘,转子2轮盘水平和竖直向倍频的增大趋势更加显著。另外,由于不对中出现在竖直方向上,水平向1X分量变化很小。
4 实验验证
参考文献[15]建立如图18所示实验装置,该装置参考典型涡扇发动机低压转子结构特征,采用“1-1-1”的支撑方式,即在“风扇转子前、套齿连接结构、低压涡轮转子后”分别使用轴承-弹性环的弹性支撑方式,以动力学相似和几何相似为理论基础将图中的实际结构进行模化。电动机和转子用膜片联轴器连接;采用电涡流位移传感器测量轮盘振动,4个通道分别为转子1轮盘水平向、垂直向,转子2轮盘水平向、垂直向。
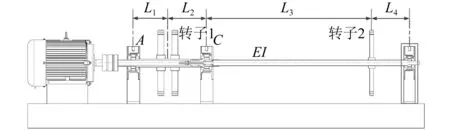
图18 超静定转子结构实验台Fig.18 Experiment rig of structure of statically indeterminate rotor system
为了使振动稳定,在转子系统实验前先进行动平衡。然后在2 400 r/min的转速下,在低压转子2轮盘的螺孔中加入15 g·mm的不平衡质量,在尾支点设置不同的不对中量,进行振动实验。
由于基频是转子的主要振动频率,在完全对中状态下没有其它频率分量。当ΔY=400 μm时,出现倍频分量,主要分量为2X振动。如图19所示。改变不对中量分别为0,50 μm,150 μm,200 μm,300 μm,400 μm,500 μm,1 000 μm后,转子2轴心轨迹图,如图20所示。

图19 ΔY=400 μm时转子1水平和垂直向振动响应Fig.19 Vibration response for horizontal and vertical direction with ΔY=400 μm
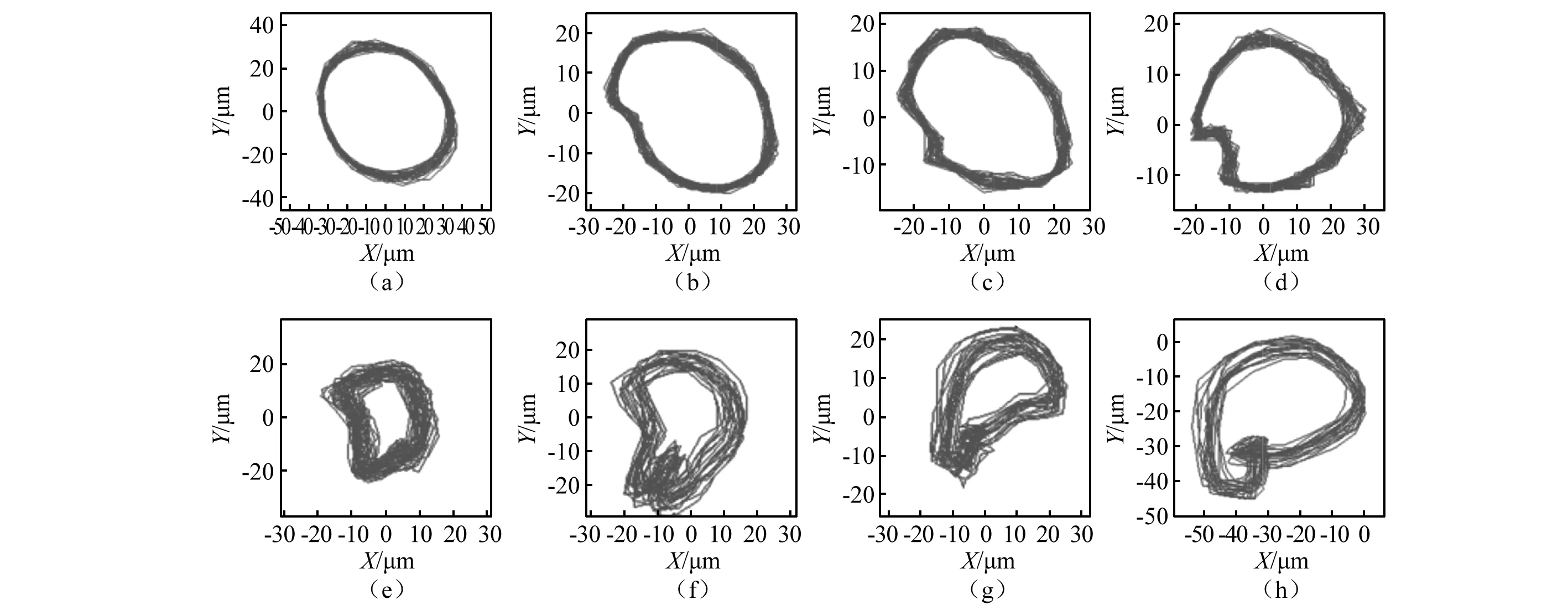
图20 转子2轴心轨迹图Fig.20 Orbits of rotor 2
轴心轨迹结果表明,在完全对中的条件下位于图像的中心。当不对中出现并逐渐增大时,轨道由近似的椭圆形变为新月形和外“8”形。当不对中量超过1 000 μm时,轴心轨迹为“8”字形。
从图21、22可知:1X分量在水平和垂直方向出现小范围波动;而水平和垂直向2X分量随着不对中量的增加非线性增大。
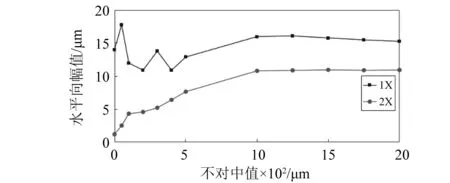
图21 转子1振动水平分量随不对中变化规律Fig.21 Vibration of rotor 1 versus misalignment magnitude in horizontal direction
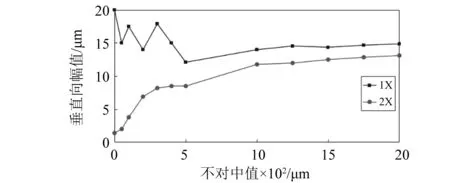
图22 转子1振动垂直分量随不对中量变化规律Fig.22 Vibration of rotor1 versus misalignment magnitude in vertical direction
对比理论和实验结果,发现两结果在振动频率成分、2X变化、轴心轨迹等基本一致;但理论结果中的振幅更高,这是因为在理论计算中没有考虑系统阻尼。
5 结 论
本文对其超静定转子系统尾部支点不对中开展了动力学解析建模、求解和实验研究,得到以下主要结论:
(1)由于该系统结构的特殊性,当尾支点出现不对中时,既要考虑不对中的动态外部激励,又要考虑不对中对系统动力学的影响。
(2)在良好对中条件下,该系统的不平衡响应与其一般振动规律相似。然而,当不对中发生时,系统会出现新的倍频成分,该成分以2X为主,随不对中量的增大,2X分量增大并不线性;2X增幅不对中较小时增长较快,2X增幅在不对中较大增长放缓;轴心轨迹由初始的近似圆,不断变化为内“8”字。
(3)形成的超静定转子不对中建模方法,能够很好的预测这类带有超静定特征的转子动力学特性及其不对中振动规律,研究结果为超静定转子系统的理论设计、动力学建模和振动控制提供了理论思路和实验依据,特别是对不对中对于整个系统动力学特性定量的影响,具有重要借鉴意义。
