台风“Soulik”东南沿海近地风剖面特性研究
2021-09-27李东亮张宏杰韩军科
李东亮,张宏杰,韩军科
(1.国家电网有限公司,北京 100031;2.中国电力科学研究院有限公司,北京 100055)
台风为沿海地区频发的自然灾害,每年台风都会造成沿海地区大量的人员伤亡和房屋倒塌。尤其是沿海地区近年来兴建了大量的大跨越铁塔,风荷载成为了这类高耸结构的控制荷载。为保证输电铁塔安全,提高结构的抗风性能,更好地了解台风的风场分布和强度具有极为重要的意义。
研究近地风沿高度的变化规律,可以较为精确地获得设计风荷载所需的风特性参数,这对于受风荷载影响较大的高耸铁塔的抗风设计尤为重要。近几十年来,世界各国对强风进行了许多的现场实测,如 Tieleman[1]通过分析大量的实测数据,得出大气表层高度随粗糙度和平均风速的增大而增大,至少为150 m的结论,并且认为达文波特的“梯度风高度”不是风速的函数,近似等于大气表层高度的两倍值。李利孝等[2]研究了台风“黑格比”边界层风剖面特征,得出摩擦速度与平均风速的关系为近似线性增长。王旭等[3]基于上海浦东地区10 m,20 m,30 m和40 m高度实测台风“梅花”数据,研究了上海浦东地区近地风的风剖面特性,得出了平均风速,湍流度和阵风因子随高度的变化规律。赵林等[4]利用浙江沿海东海塘观测站实测的3个台风(“海棠”、“麦莎”和“卡努”),统计得到风剖面幂指数随台风中心与观测塔的距离增大而减小,并且在A类地貌下,大于我国规范建议值0.12。Li等[5]以某输电塔上5台不同高度的三维超声风速仪实测数据为基础,分析了我国福建地区近地风场特性。并依据指数率模型拟合出风剖面幂指数和湍流强度剖面。Shu等[6]以香港沿海气象观测站用杯型风速计和多普勒雷达同步实测数据得出了季风和雷雨大风的风剖面形状,并导出了幂率和指数率模型中包含的拟合参数。然而,由于野外监测周期长,设备维护成本高昂,实时台风数据难以采集,使得我国缺乏对沿海地区近地风剖面的研究。基于此,选取福建宁德地区500 kV输电杆塔作为观测基站,研究了台风“Soulik”过境时的近地风场特征。以期为台风影响区的输电铁塔等高耸结构抗风设计提供参考。
1 观测地点及测量程序
1.1 台风Soulik的介绍
2013年的07号热带风暴“Soulik”于西北太平洋上生成,42 h后升级为超强台风,最大风力16级,以20 km/h的风速移动。于2013年7月13日16时在中国福建省连江县黄岐半岛沿海登陆,13日17时再次削减为热带风暴。此次台风具有强度高,路径稳定、影响范围广的特征。
1.2 场地概况和仪器
实测场地位于福建省宁德市霞浦县牙城镇洪山村,选取550 kV宁德的笠里核电送出线路上的52#杆塔为研究对象。该场地为南、北方向山丘环绕的河谷型地貌,介于北纬26°25′~27°09′,东经119°46′~120°26′,北距温州、南距福州均160 km。在塔身上安装有5个三维超声风速仪,分别距离地面15 m,27 m,53 m,67 m和82 m。5个风速仪同步计量风速,采样频率为10 Hz,如图1所示。采样的时段为2013年7月13日0时—2013年7月13日22时,并按10 min平均时距进行子样本分割。
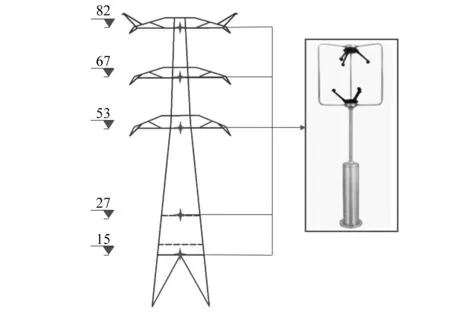
图1 仪器安装位置Fig.1 Installation position of the instrument
2 数据处理方法
2.1 风速廓线
在大气边界层内,用风速廓线理论研究平均风速沿高度的变化规律。常用的风速廓线理论模型包括指数率模型、对数率模型[7]和Deaves-Harries模型[8-10]。
2.1.1 指数率模型
Davenport通过大量的实测研究,提出平均风沿高度呈指数分布。由于指数率模型形式简单,已被纳入我国建筑结构荷载规范[11],经验表达式为
(1)
式中:zref为标准高度;U(zref)为标准高度处的风速;α为地面粗糙度指数。
2.1.2 对数率模型
在中性大气条件下,大气边界层的近层和远层存在一定重叠区域。这一区域的风速同时满足壁面定律和速度亏损定律,以此得到风剖面的对数率表达式为
(2)
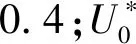
(3)
式中,u′,v′和w′分别为纵向脉动风速、横向脉动风速和竖向脉动风速。
研究表明[16-17],当u′和v′二者任意风向与主风向一致时,式(3)可简化为
(4)
2.1.3 Deaves-Harries模型
Deaves改进了对数律模型,使得改进后的对数率模型完全适用于全边界层,得到的Deaves-Harries模型表达式为
(5)
式中,zg为边界层高度,计算表达式为
(6)
式中,B′为经验参数,一般取6;f为科里奥利参数,文中取 7.554×10-5s-1。
2.2 湍流度
湍流强度是衡量湍流强弱的相对指标,是描述大气湍流运动的重要特征量。定义为平均时距内脉动风速的标准差与相应时距内纵向平均风速大小的比值,表达式为
(7)
式中:σi为脉动风速u(t)和v(t)的均方根;u,v,w分别为纵向、横向及竖向脉动风速分量。
三维超声风速仪输出3个方向的风速分量ux(t),uy(t)和uz(t),本文采用矢量分解法求得平均风速U,风向角φ,计算表达式为
(8)
(9)
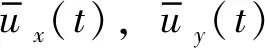
脉动风速可依据下式计算
u(t)=ux(t)cosφ+uy(t)sinφ-U
(10)
v(t)=-ux(t)sinφ+uy(t)cosφ
(11)
(12)
2.3 阵风因子
自然风的脉动强弱也可用阵风因子来表示,阵风因子定义为高度z处阵风持续周期tg内平均风速峰值与平均时距内平均风速的比值。其一般表达式为
(13)
(14)
(15)
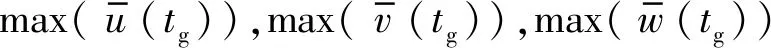
3 实测数据处理
3.1 风速廓线理论及相关参数分析
3.1.1 平均风速与风向角
规定实测风向角以正北方向为0°,顺时针转向为正方向。2013年7月13日0:00—21:00期间不同高度z处的10 min平均风速U和风向角φ随时间的变化曲线,如图2所示。由图2可知:平均风速的大小与风速采集的高度成正比关系,各高度处平均风速,风向角变化趋势基本一致。各高度平均风速在2013年7月13日13:00:00—13:10:00时段达到峰值,15 m,27 m,53 m,67 m和82 m对应的最大平均风速分别为15.24 m/s,16.67 m/s,17.22 m/s,17.72 m/s和18.24 m/s。对应的风向角分别为73.58°,83.23°,80.39°,74.21°和76.40°。之后平均风速开始下降,风向角在2013年7月13日07:00:00趋于平稳状态。
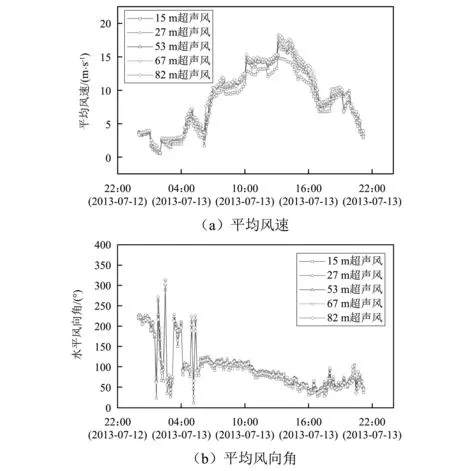
图2 平均风速、风向角变随时间变化Fig.2 Variation of mean wind speed and wind direction angle with time
3.1.2 相关参数分析
理论模型中提及到了粗糙度指数、摩擦速度和边界层高度等相关参数,本文将逐个对其展开分析。
(1)粗糙度指数α
粗糙度指数α主要与地面的粗糙程度有关,它是结构抗风设计的一个重要参数。粗糙度指数随10 m高度处10 min平均风速的变化情况,如图3所示。粗糙度指数是按15 m,27 m,53 m,67 m和82 m高度处的10 min平均风速按照指数分布拟合得到。图3中结果表明:当平均风速小于12 m/s时,粗糙度指数α随平均风速的增大而减小,数据较为离散,最大值达到0.58,最小值为0.026;当平均风速大于12 m/s时,粗糙度指数基本不随平均风速发生变化,与Shu等所得结论基本一致。
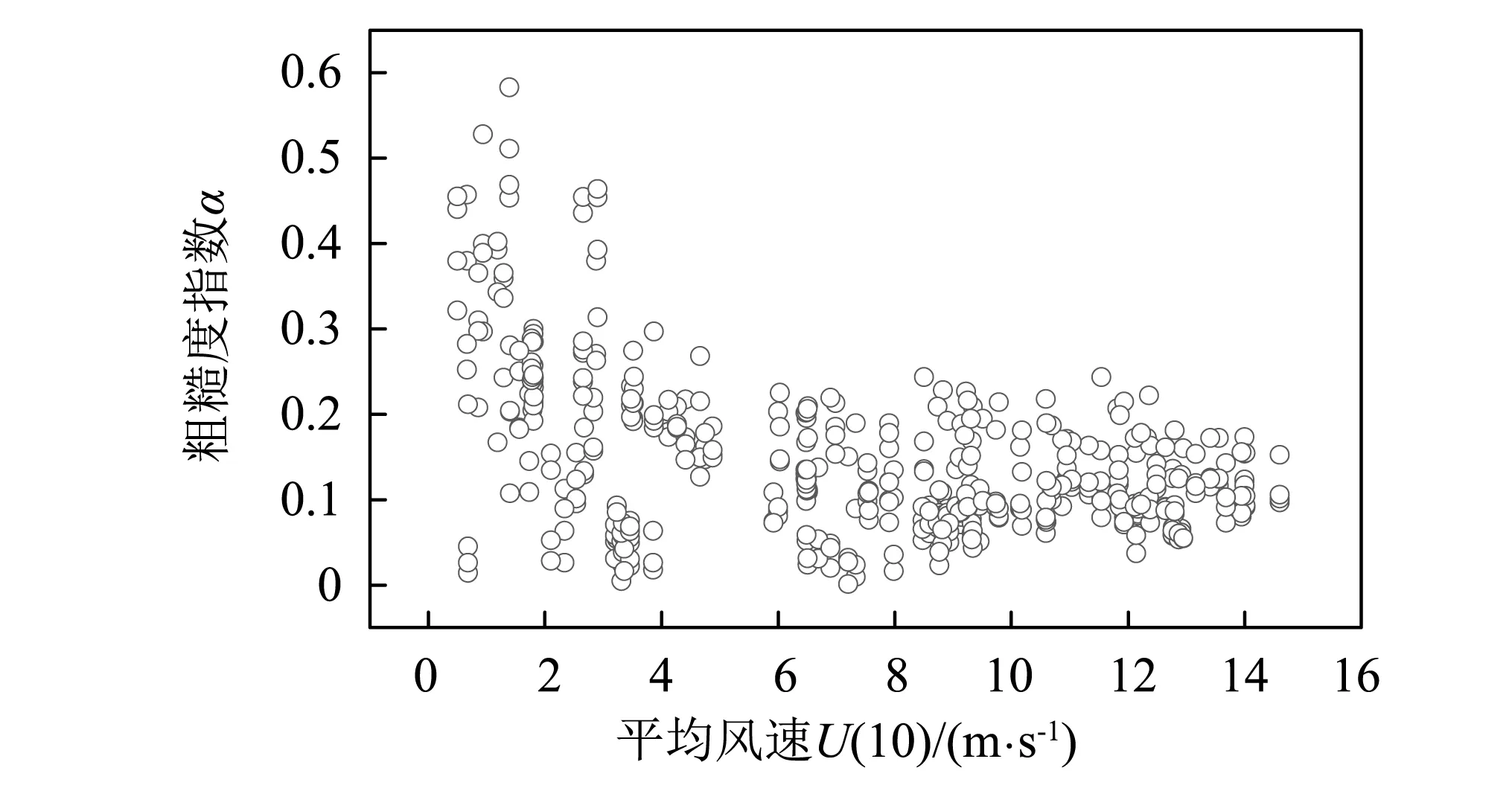
图3 粗糙度指数随平均风速的变化Fig.3 Roughness index changes with mean wind speed
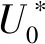
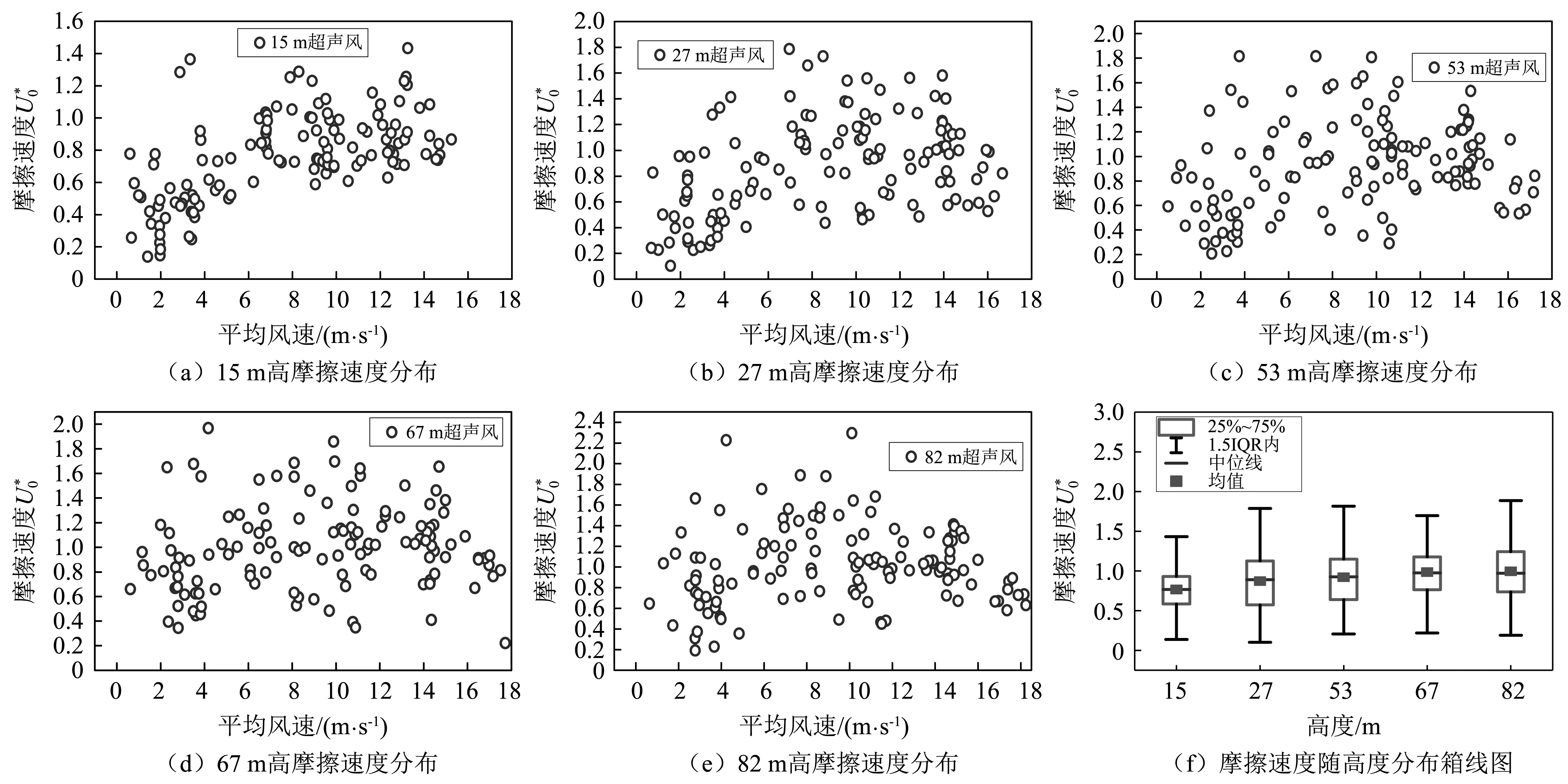
图4 摩擦速度随平均风速及高度的变化Fig.4 Variation of friction velocity with mean wind speed and height
(3)边界层高度zg
边界层高度指自由大气层不受地面摩擦力影响的临界高度,边界层高度受平均风速的影响。图5(a)所示为由公式计算的边界层高度zg随平均风速的变化情况。从图6(a)可知:边界层高度随平均风速的增大而增大,可以得出边界层高度zg的平均值为2 007.89 m,远高于我国规范规定的B类地貌下的边界层高度350 m。而本文所得结论与王旭等研究及文献[18]所得结论相近。边界层高度随高度的变化如图5(b)箱线图所示。可以看出不同高度处边界层高度的分布有着明显的差异。边界层高度的均值随高度的增大而增大,而中位数随着高度的增加与均值的差异越来越大。
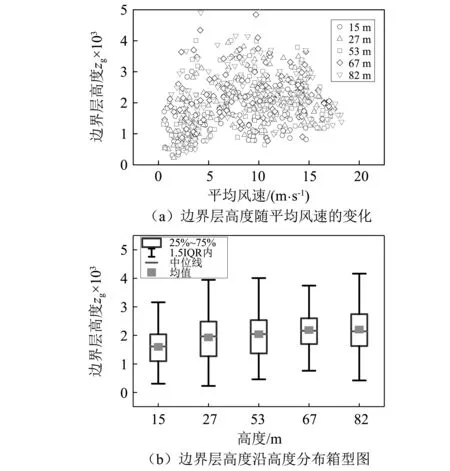
图5 边界层高度随平均风速的变化边界层高度沿高度分布箱型图Fig.5 Box diagram of boundary layer height distribution along the height as the change of boundary layer height with average wind speed
3.1.3 风速廓线实测分析
平均风速剖面随时间的变化曲线,如图6所示。由于受地形地貌以及仪器安装条件的限制,10 m高度处未设置三维风速仪,采用53 m,67 m,和83 m高度处的风速按指数率计算出10 m高度处的风速。以U(z)与10 m高度处平均风速的比值为横坐标,结果表明,平均剖面随着时间的推移而发生改变,在6:00时刻由于风速增大风剖面变化明显,各个剖面之间存在着显著的差异。在初始时刻,各测点高度的平均风速与10 m高平均风速的比值近似相等。随着时间的推移,比值开始增大,U(82)与U(10)的比值从1.06增大到1.37。图7(a)给出了5组不同时段平均风速下对应的风剖面。图7(a)结果表明,5组风速剖面呈现出两种不同的变化趋势。当风速小于12 m/s时,平均风速随高度的变化曲线相对平缓;当风速超过12 m/s时,平均风速随高度变化较为剧烈。利用平均风速大于12 m/s的实测数据绘制的平均风速剖面图,如图7(b)所示。并且与该实测数据拟合的指数率模型、对数率模型和Deaves-Harris模型进行对比。结果表明,当平均风速大于12 m/s时,台风“Soulik”的平均风速沿高度的变化规律与指数率模型、对数率模型基本吻合,而采用Deaves-Harris模型对台风“Soulik”平均风沿高度的变化描述不够准确。这与王旭等的研究所得结论不同,原因可能因为王旭等所研究的范围仅在40 m高度以内。

图6 风剖面随时间变化Fig.6 Variation of wind profile with time
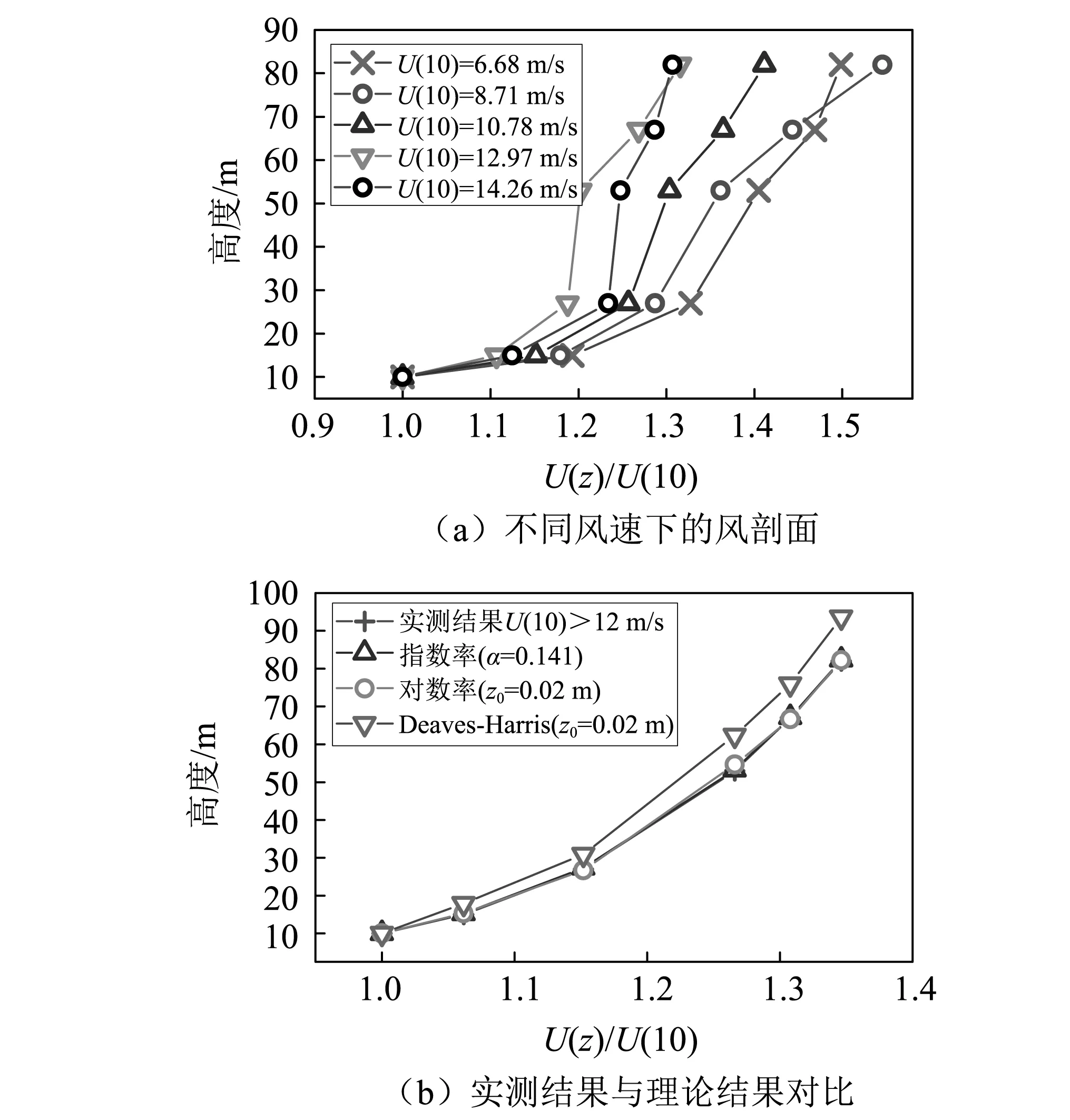
图7 不同风速下风剖面实测结果与理论结果对比Fig.7 Comparison between measured results and the oretical results of wind profiles at different wind
3.2 湍流度剖面
纵向湍流度随高度的变化关系以及美国、日本[19]和欧洲规范[20]规定的湍流度剖面,如图8所示。从图8可知:纵向湍流度随着高度的增大而减小。当风速较小时,风速大于12 m/s的湍流度更能反应台风在中性大气层中的湍流特性。与各国规范对比发现,实测湍流度随高度的变化与规范的经验变化曲线有着一致的变化趋势。但各高度处纵向湍流度实测值均小于规范经验值,说明台风“Soulik”的湍流剖面不适合用3种规范的经验表达式来描述。因此,对平均风速大于12 m/s的纵向湍流度进行了指数型拟合,拟合后的表达式为Iu=0.138(45/z)0.2。
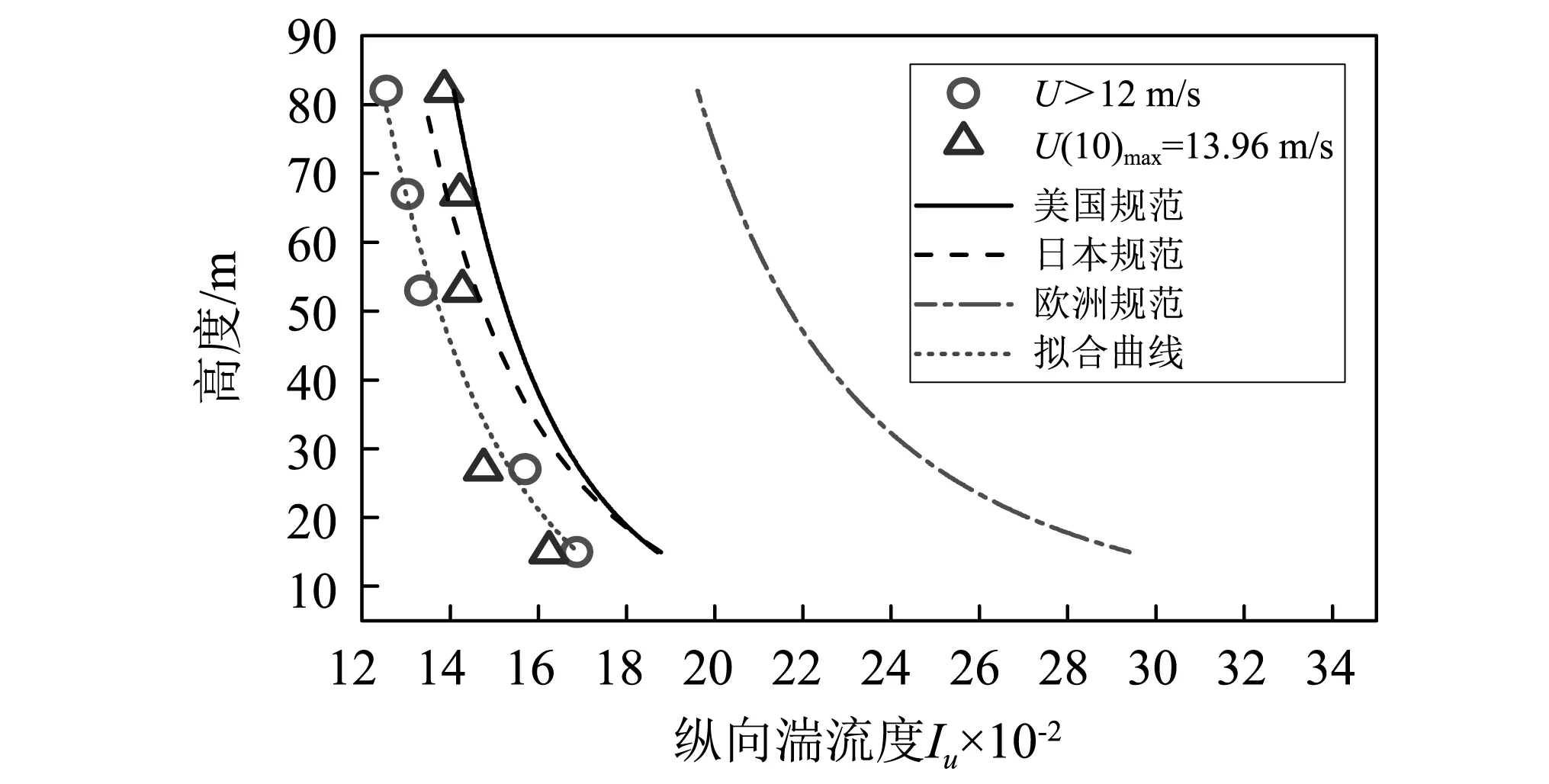
图8 纵向湍流度随高度变化Fig.8 Longitudinal turbulivity changes with height
由于国内外对横向和竖向湍流剖面的研究欠缺,各国规范也没有相应的经验表达式。因此本文对横向和竖向的湍流度实测结果进行了类似于纵向湍流度剖面的指数型拟合,分别得到横向剖面的表达式为Iv=0.084(24/z)0.3,竖向剖面的表达式为Iw=0.137(60/z)0.3,如图9、图10所示。
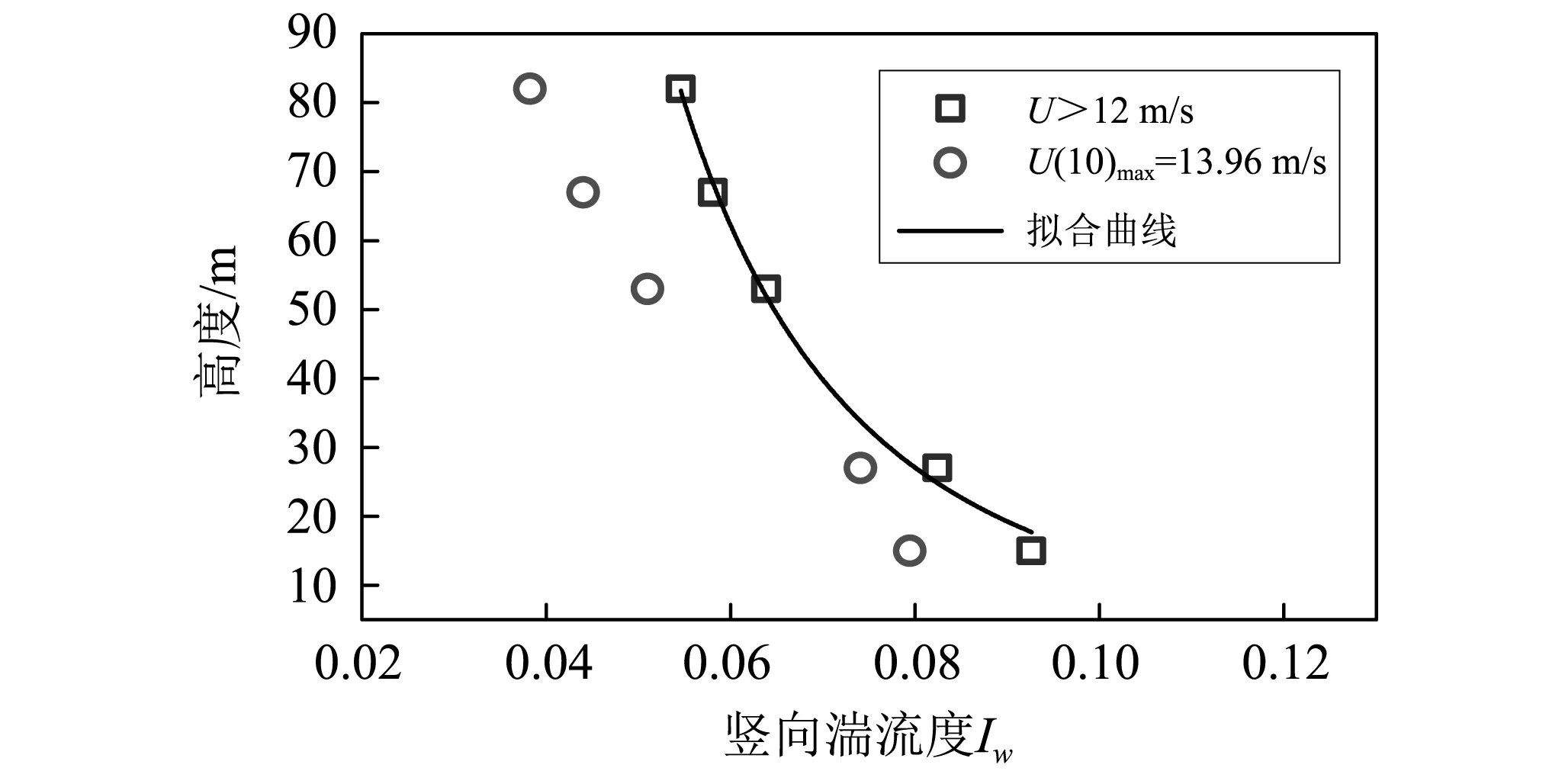
图9 横向湍流度随高度变化Fig.9 Transverse turbulivity changes with height
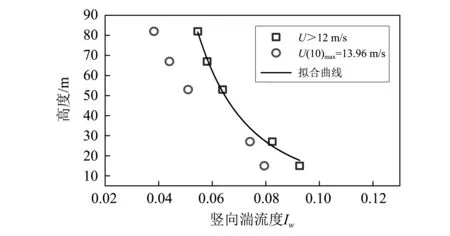
图10 竖向湍流度随高度变化Fig.10 Vertical turbulivity changes with height
3.3 阵风因子剖面
实测阵风因子随高度的变化规律,如图11所示。结果表明各向阵风因子随高度的增大而减小。由于阵风因子剖面的表达式尚无相关规定,本文对各向阵风因子进行了形如Gi=α(z/10)β的拟合。从图11可知:各向实测阵风因子随高度的变化均能与拟合结果较好地吻合,说明拟合表达式可以用来描述本次台风地阵风因子剖面。
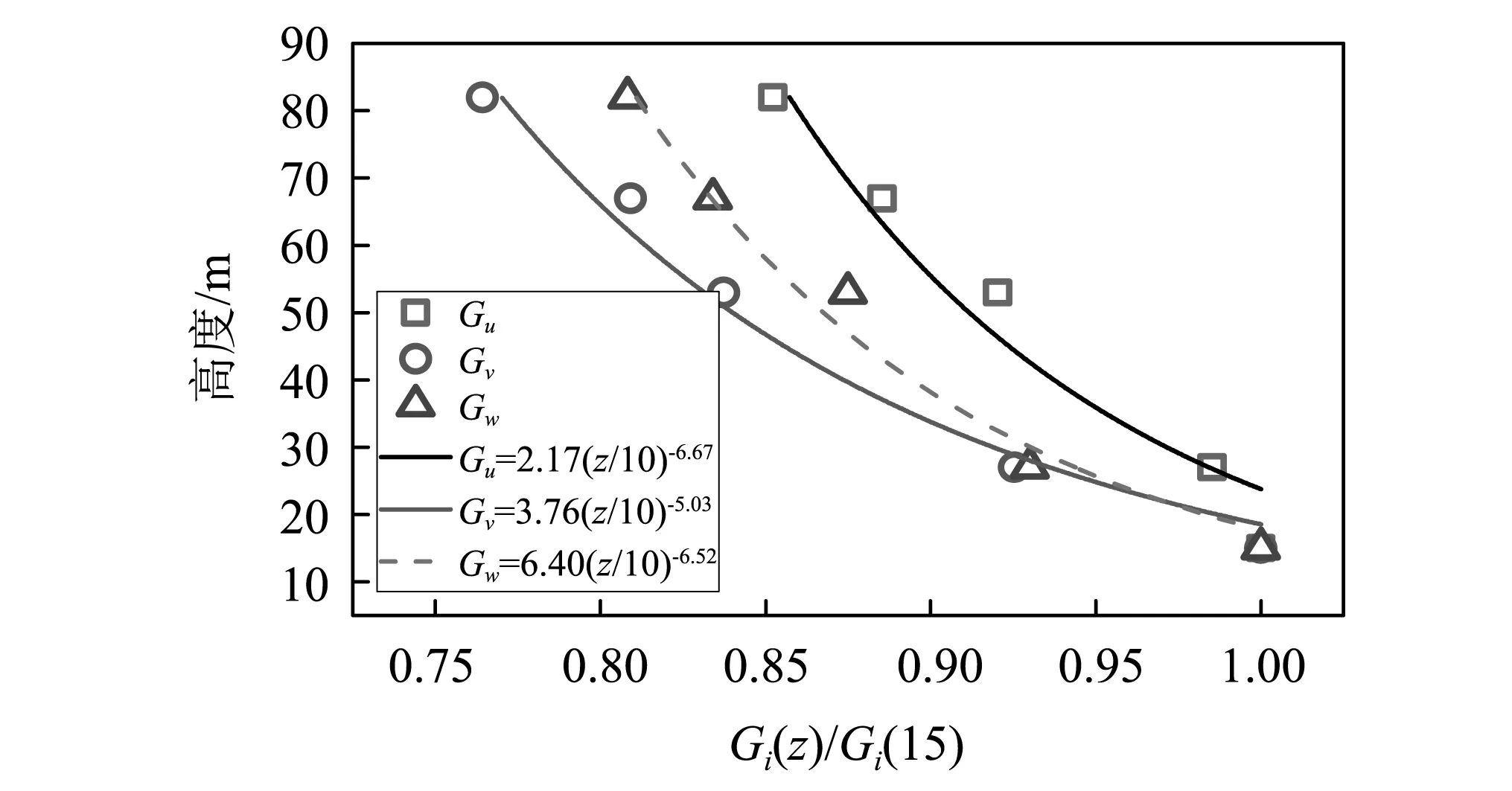
图11 阵风因子随高度变化Fig.11 Variation of gust factor with altitude
4 结 论
本文利用福建宁德地区500 kV输电杆塔为观测点,通过在15 m,27 m,53 m,67 m和82 m高度处实测台风“Soulik”数据,进行了近地风剖面及相关参数的研究,得到如下结论:
(1)当平均风速小于12 m/s时,粗糙度指数α随平均风速的增大而减小,数据较为离散,最大值0.580,最小值0.026。当平均风速大于12 m/s时,粗糙度指数基本不随平均风速变化,与Shu等所得结论基本一致。
(2)当风速小于12 m/s时,摩擦速度分布较为离散,随平均风速的增大而增大;当平均风速大于12 m/s时,摩擦速度分布由离散状态开始变为集中状态,此时,摩擦速度基本不随平均风速变化。
(3)依据公式计算出的边界层高度随平均风速的变化不明显。实测数据平均值为2 007.89 m,远高于我国规范规定边界层高度在B类地貌下的350 m,本文所得结论与王旭等和Li等所得结论相近。
(4)台风“Soulik”平均风速沿高度的变化规律可以用指数率和对数率模型来描述。美国、日本和欧洲规范中纵向湍流剖面的经验表达式均不能与本次台风纵向湍流剖面相吻合。本文通过指数型拟合分别得到了纵向、横向和竖向湍流剖面的表达式。
(5)由于阵风因子剖面的表达式尚无明文规定,本文对实测阵风因子进行了形如Gi=α(z/10)β的拟合。实测阵风因子随高度的变化均能与拟合结果较好地吻合,并获得了阵风因子的经验表达式。
