主梁结构形式对大跨度钢桥车致结构噪声的影响
2021-09-27李小珍龚振华
李小珍,龚振华
(西南交通大学 土木工程学院,成都 610031)
由于具有质量轻、强度高、施工便捷等特点,大跨度轨道交通钢桥在现代化城市中的应用越来越广泛。但相较于以低频噪声(20~200 Hz)为主的混凝土梁,钢梁的结构噪声主要集中在中、高频段(200~1 000 Hz),声辐射频率更宽,对沿线居民的噪声污染更加严重[1-2]。
已有的对桥梁结构噪声的控制措施可分为两类:一是在设计阶段进行降噪设计,包括对主梁的结构形式进行选型、参数优化,增大桥梁阻尼;二是对已建成的桥梁采取降噪措施,包括设置减振扣件,铺设减振轨道系统,在钢构件表面敷设阻尼材料等[3-4]。然而第二类后期措施不仅会影响交通线路正常运行,也会产生不必要的经济支出。因此,对于重要交通线路上的大跨度桥梁,在前期进行充分的降噪设计是十分必要的。
为了研究桥梁结构噪声的辐射规律,国外的Walker等[5-8]已开展了许多针对桥梁结构噪声的现场试验和数值计算。国内的高飞等[9]建立三维桥梁振动模型和二维声场分析模型,利用有限元软件对混凝土高架桥梁的结构噪声进行了预测。李小珍等[10]基于车-线-桥空间耦合振动理论和稳态声辐射边界元法提出了高速铁路桥梁的结构噪声全频段预测模型,并以32 m双线预应力混凝土简支箱梁的现场实测结果验证了模型的可靠性。Li等[11-13]提出了一种具有更高计算效率且确保精确度的2.5维边界元模型,在考虑时变的车-轨-桥动力相互作用下,通过计算桥梁的空间模态声传递矢量和桥梁的模态坐标响应来计算桥梁噪声。Song等[14-15]提出了波导有限元模型和波导有限元-二维边界元混合模型对高速列车三跨混凝土连续箱梁的结构噪声进行预测。考虑到钢桥有结构复杂、以中高频噪声为主等特性,Augusztinovicz等[16-19]基于统计能量分析原理分别对钢混叠合简支高架桥、多跨连续钢箱梁、大跨度钢箱斜拉桥和多跨连续简支叠合梁桥的结构噪声进行了数值计算和试验验证。
本文基于统计能量分析(statistical energy analysis ,SEA)方法,以列车-轨道-桥梁耦合频域模型计算出的轮轨系统向桥梁系统传递的频域支撑力为激励,建立大跨度钢桥的结构噪声预测模型。并以重庆千厮门大桥的现场试验结构为例,验证模型的可靠性。最后对大跨度钢桁梁、钢箱梁桥结构噪声的频域分布规律、辐射规律、构件声贡献量等进行对比分析。
1 基于SEA的大跨度钢桥结构噪声预测模型
1.1 子系统的划分
为了确保对高频、高密度模态的复杂结构进行动力响应计算,需按照相似共振模态为一组对结构子系统进行划分。一个相似模态群在分析带宽Δf内的模态数N由该子系统的特征参数模态密度n(f)确定
N(f)=n(f)·Δf
(1)
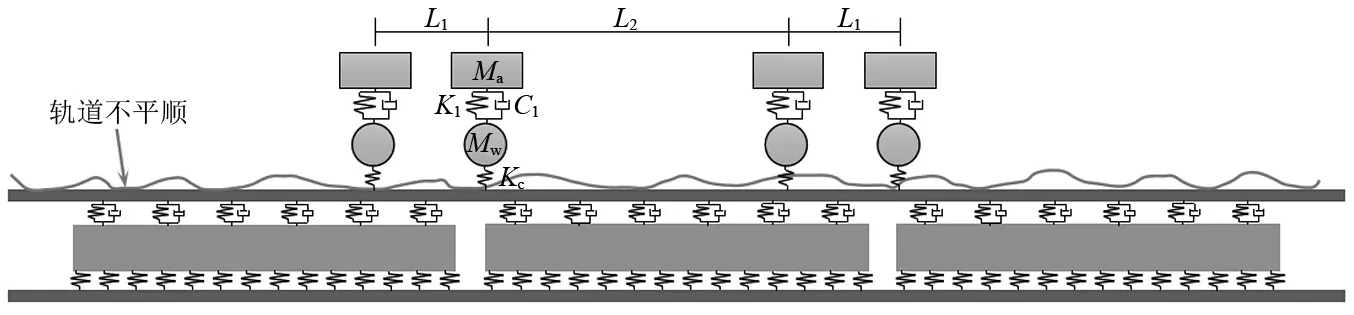
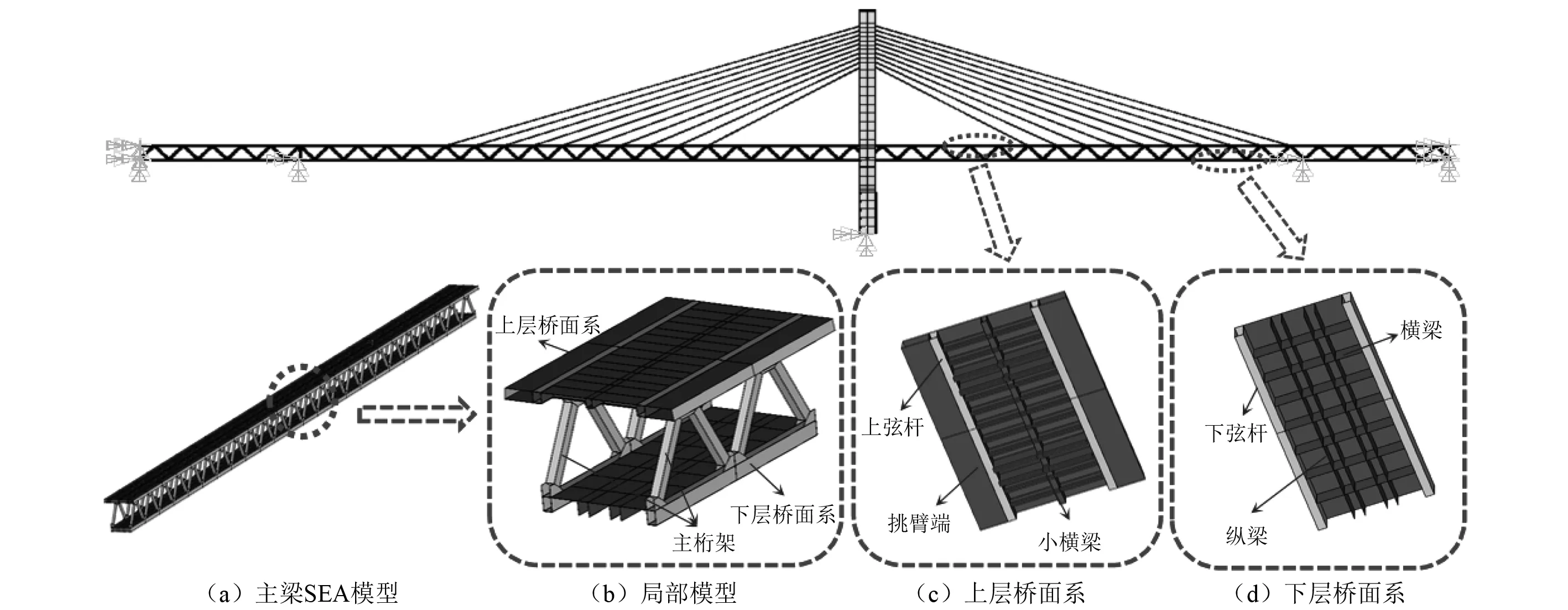
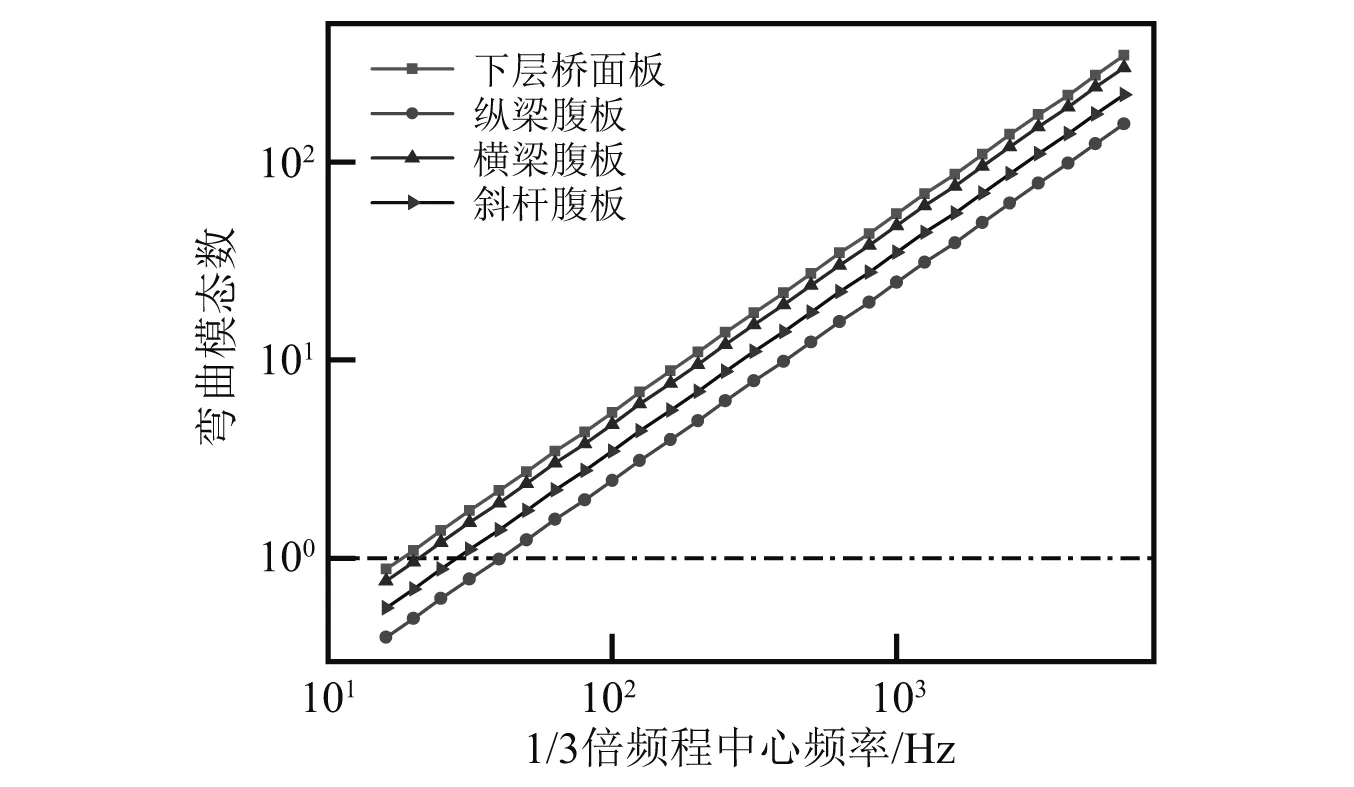
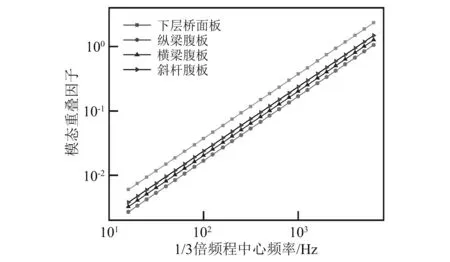
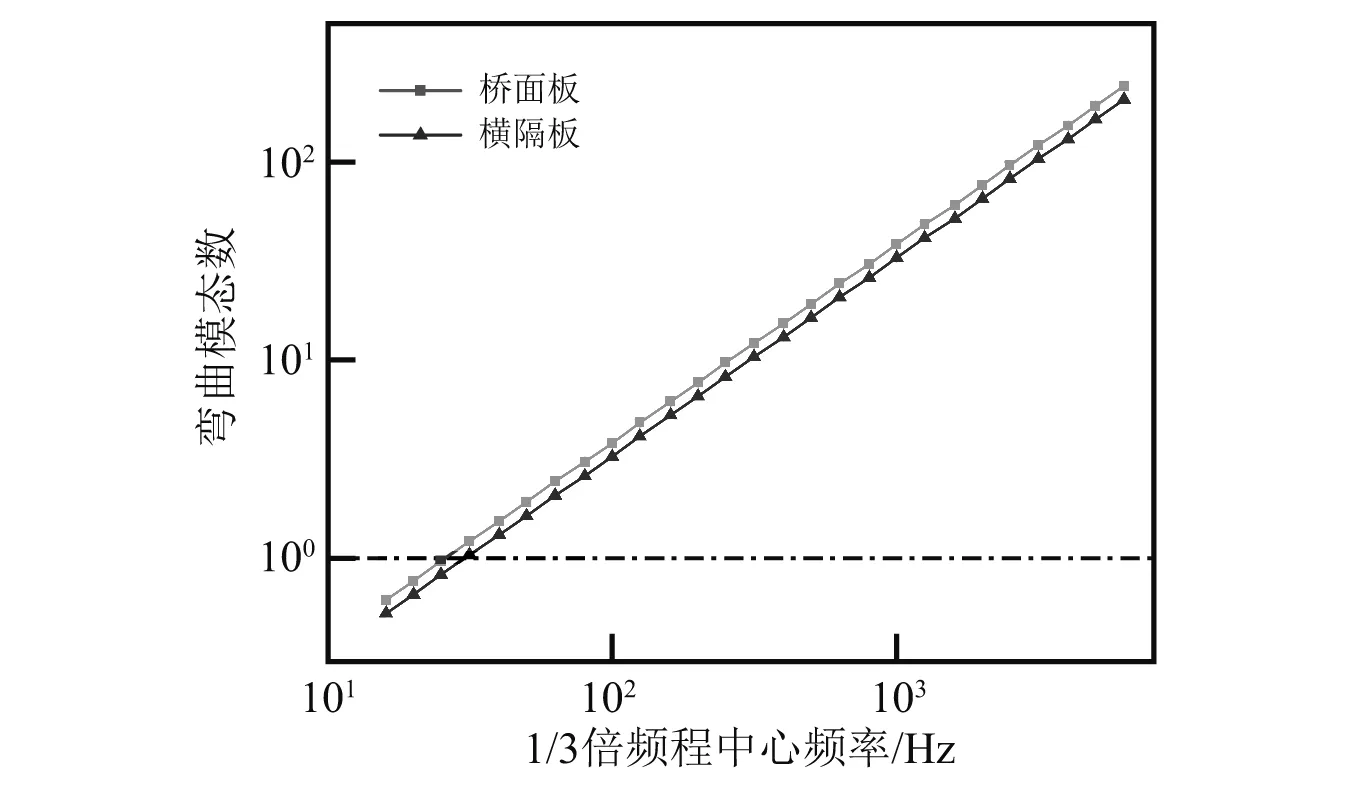
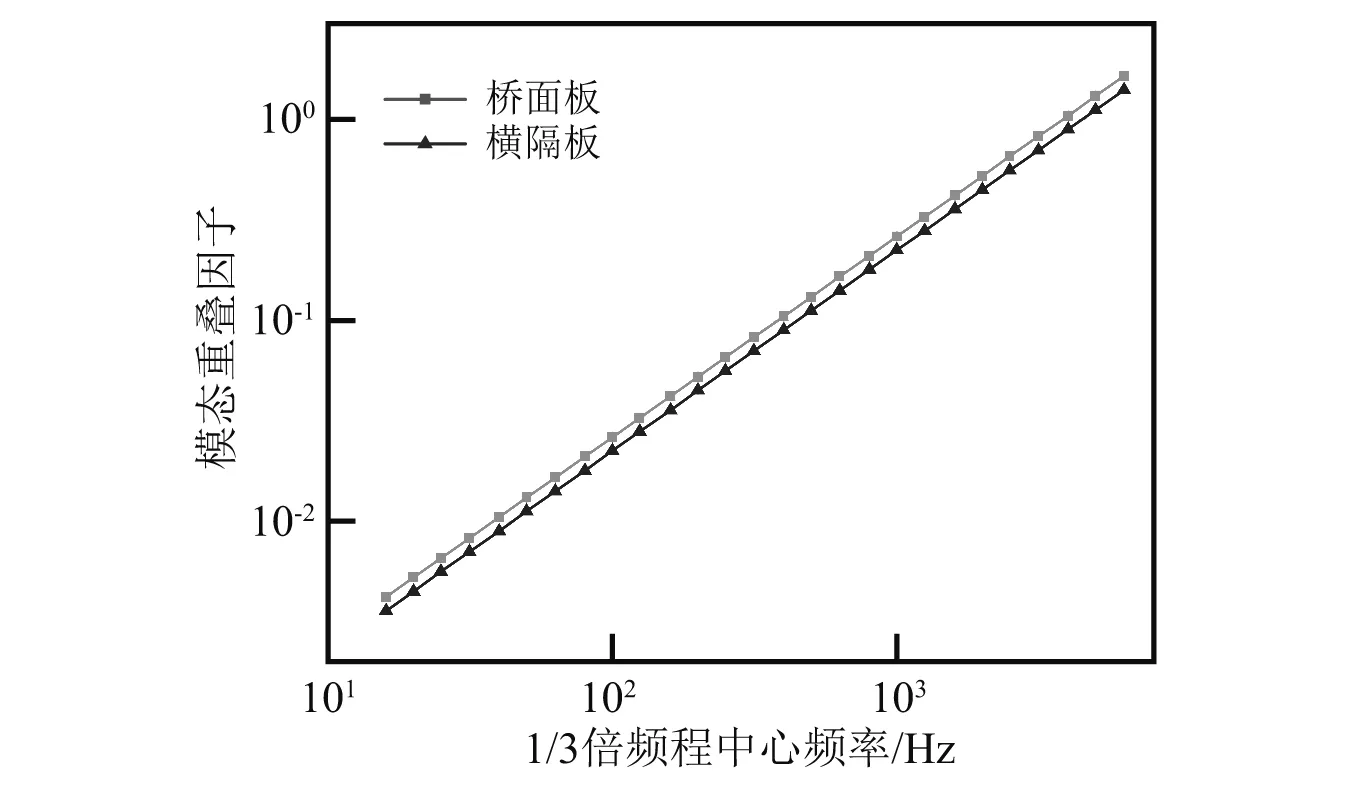
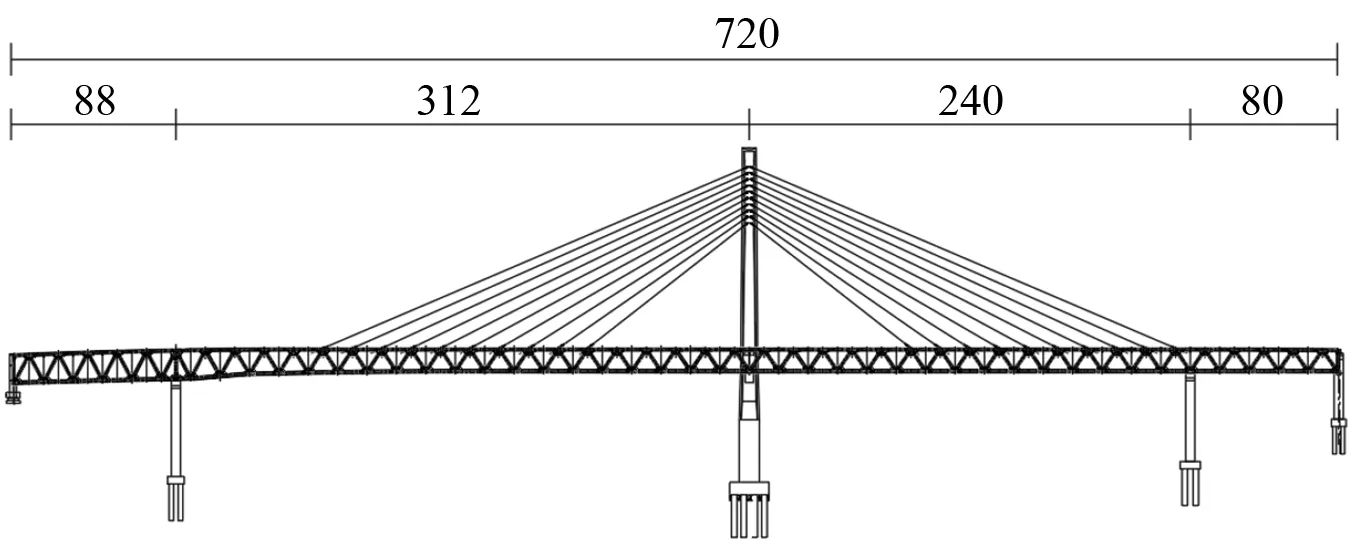
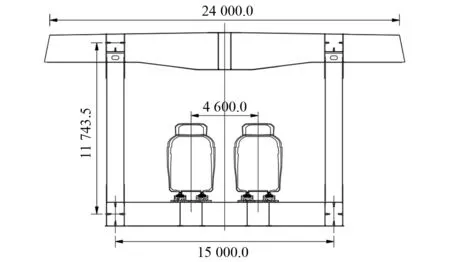
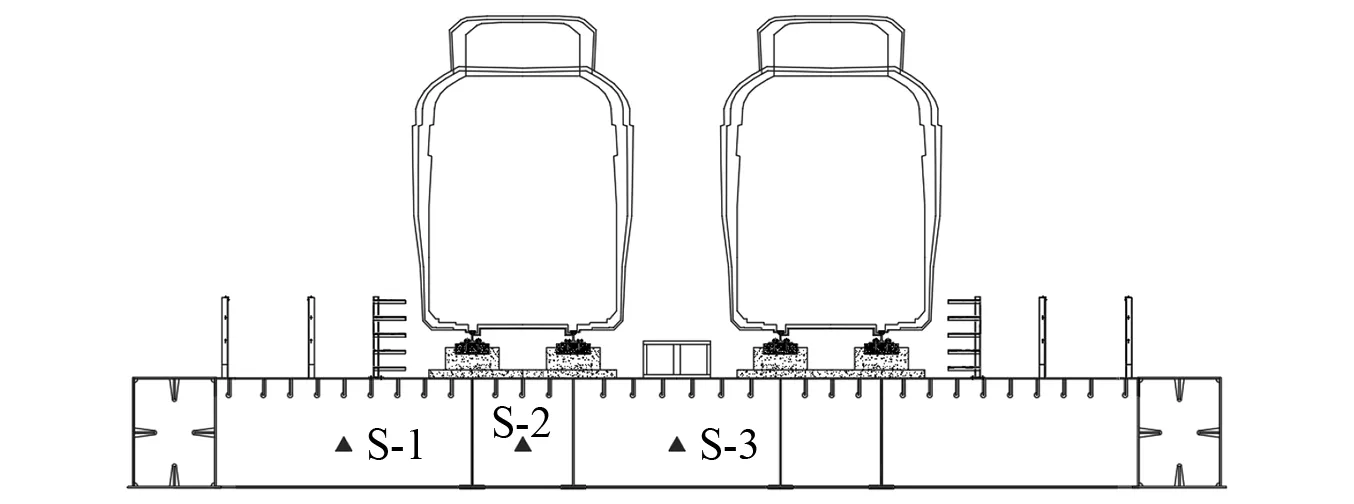
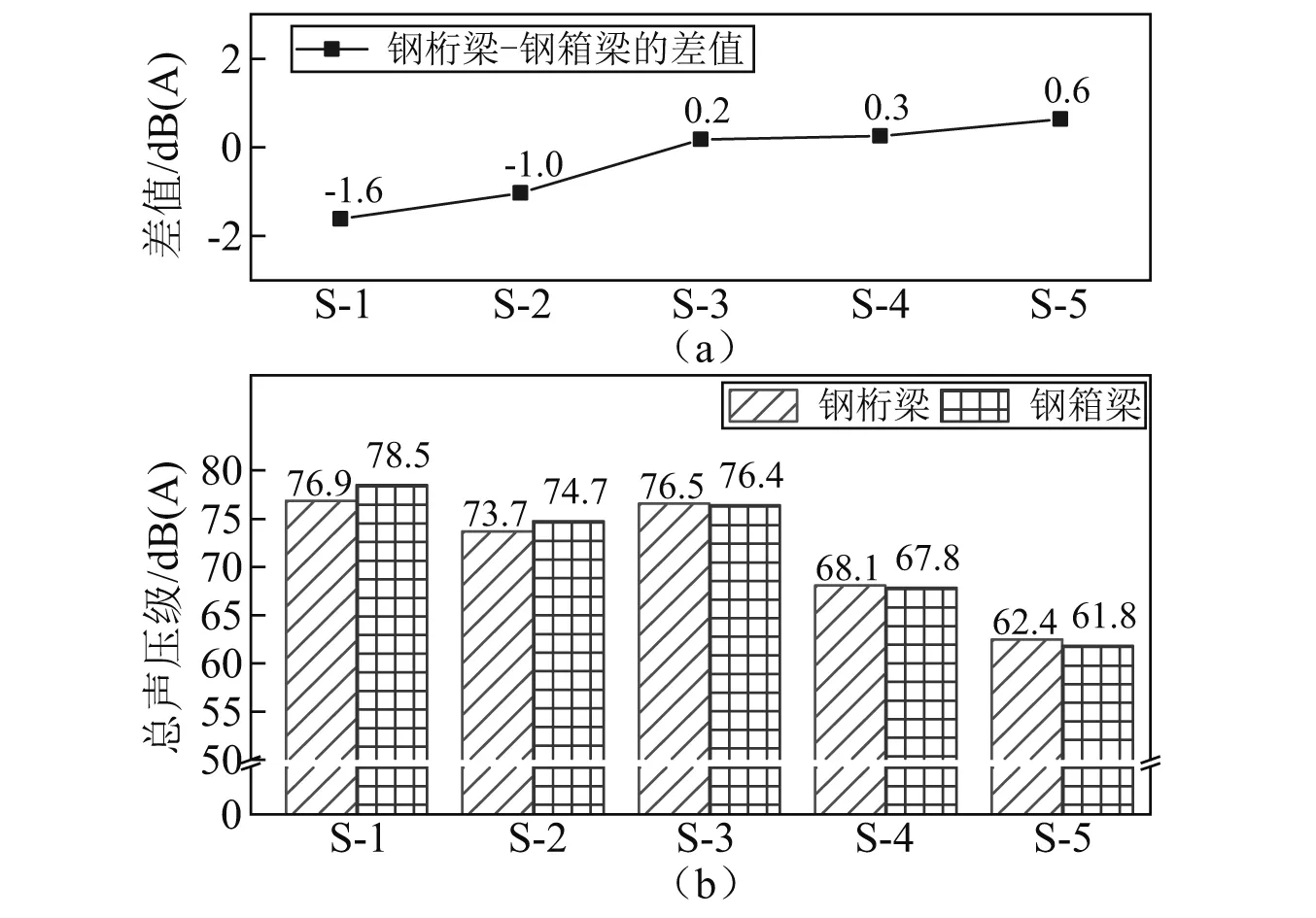
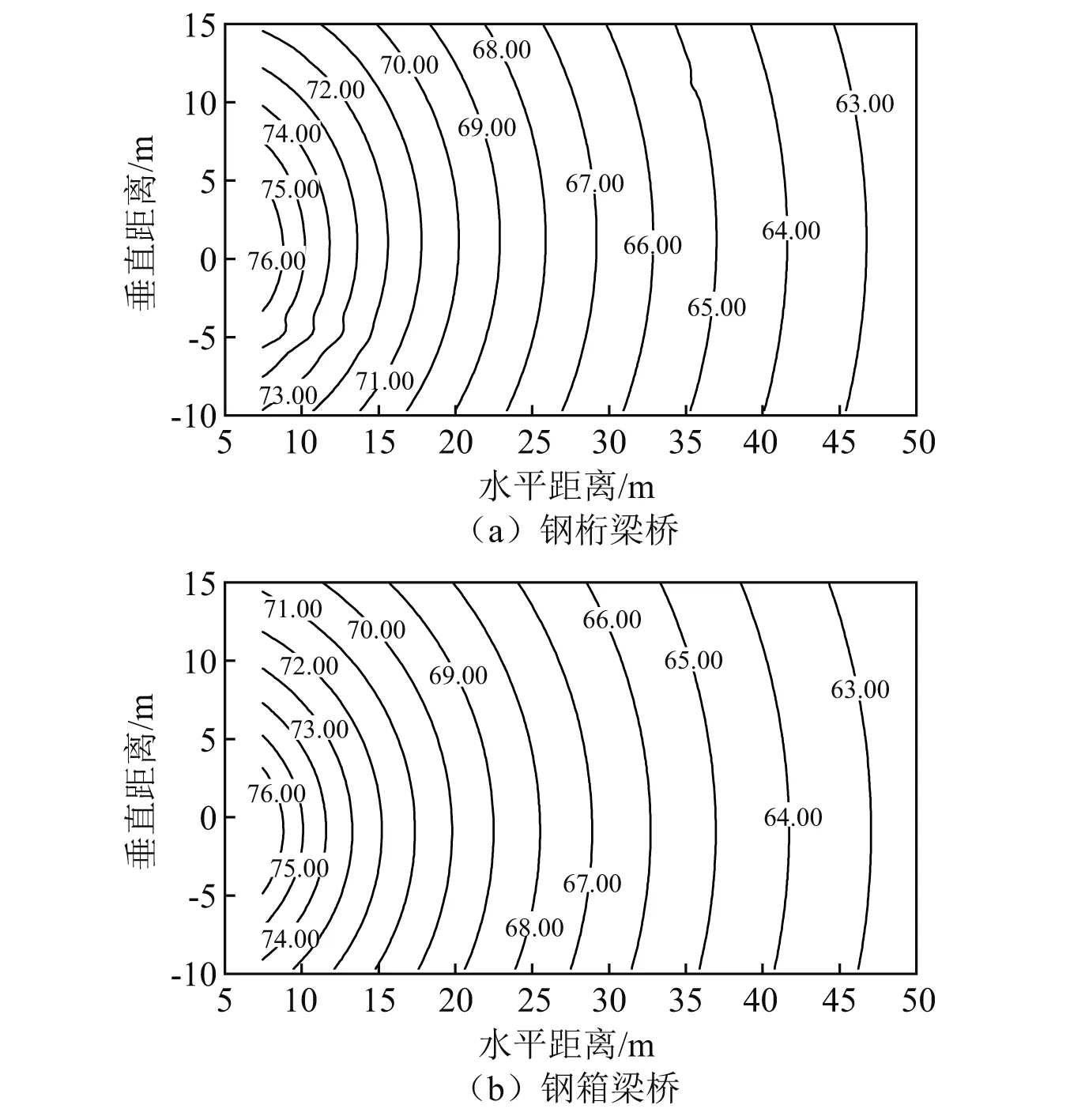
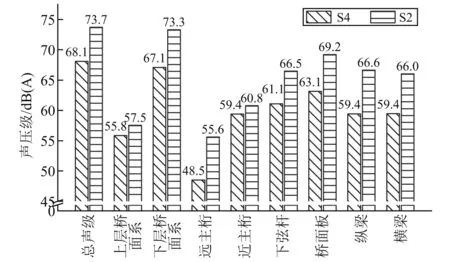
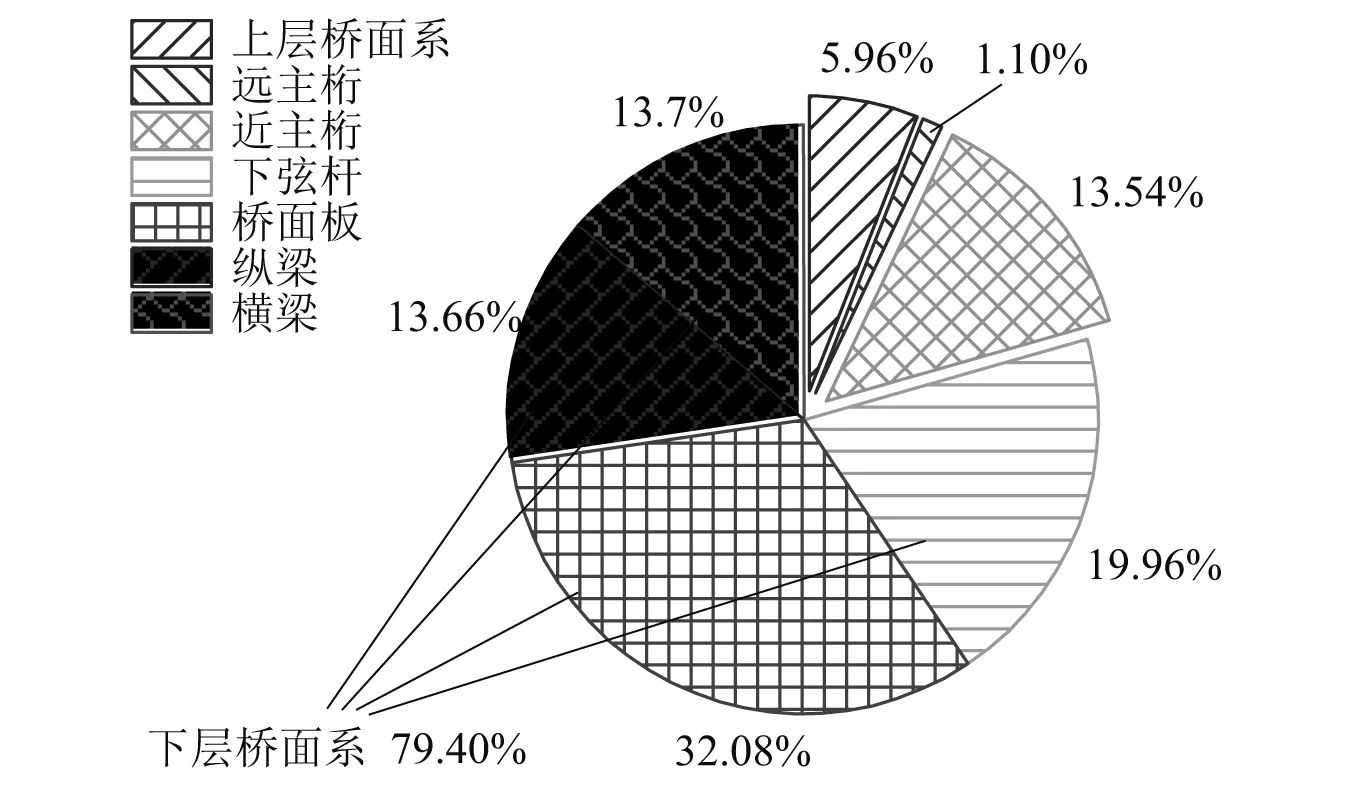
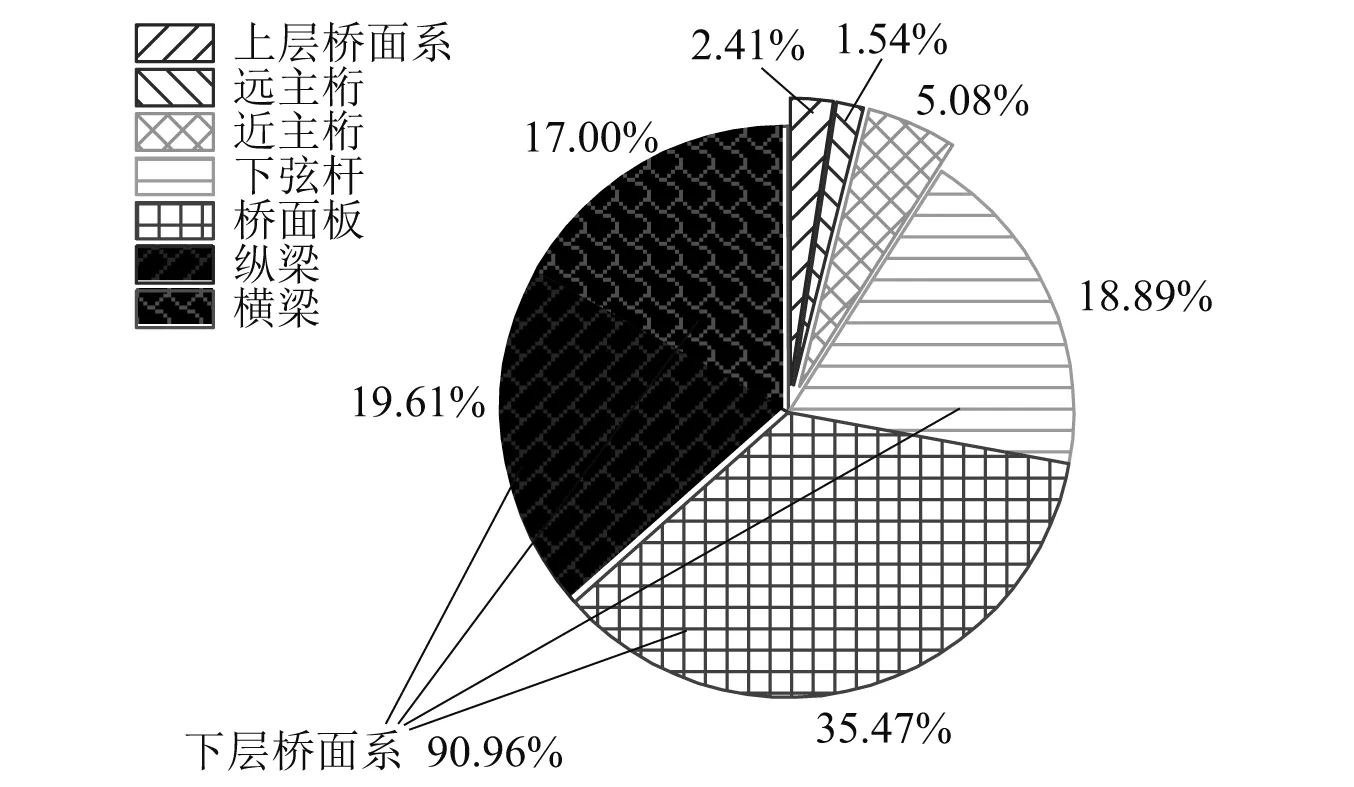
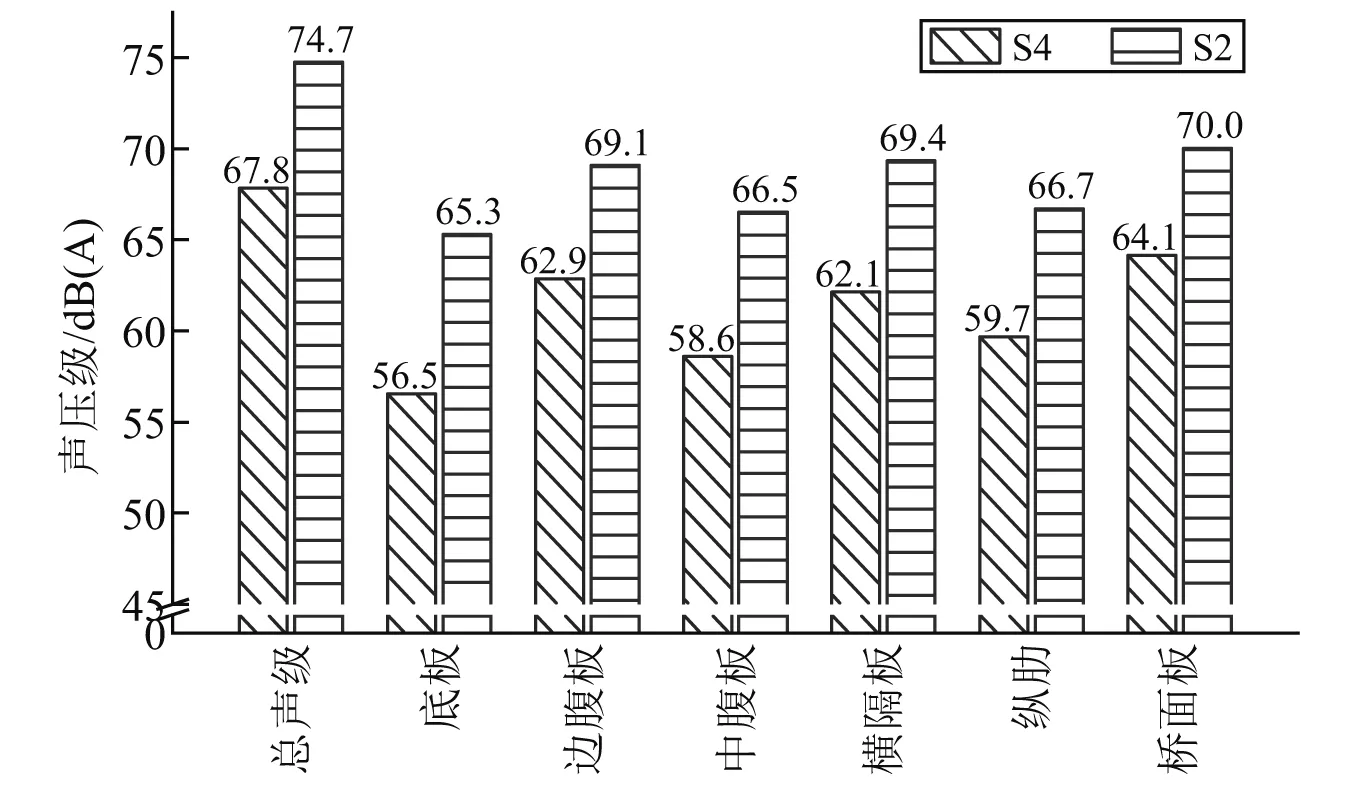
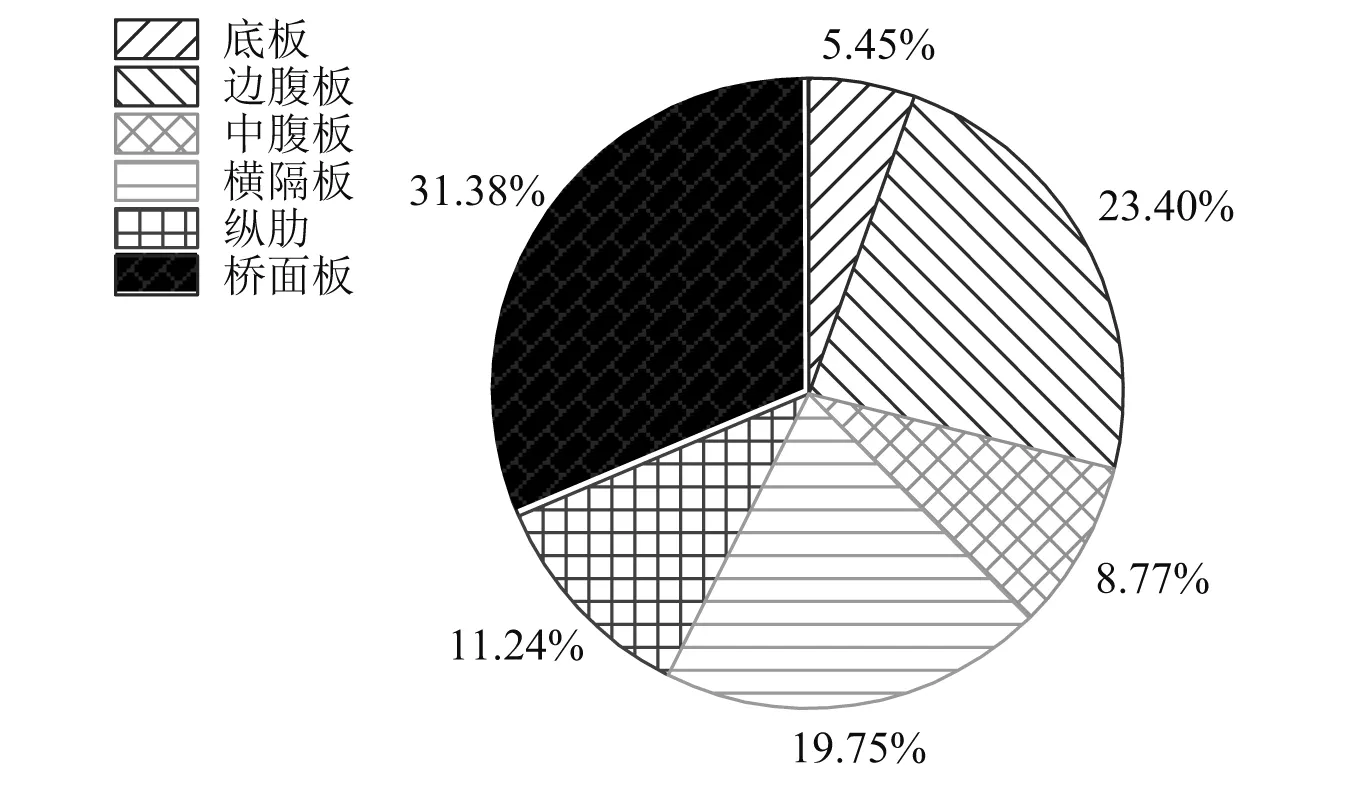
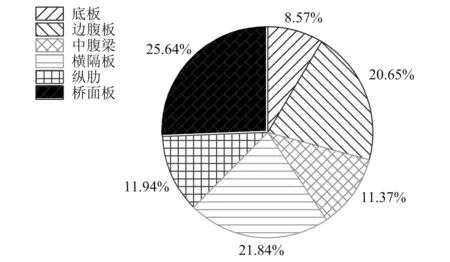
根据子系统模态数的大小可对研究范围进行如下划分:N≤1为低频区;1 任意SEA子系统i可看作一个独立的储存振动能量的构件,其振动损耗功率[20]可表示为 (2) 式中,Pid,ηi,Ei,Mi为在分析带宽Δω内对子系统所有振型的平均损耗功率、内损耗因子、振动能量和质量。 从子系统i传递到子系统j的纯功率流可表示为 Pij=P′ij-P′ji=ωηijEi-ωηjiEj (3) 式中:P′ij为从子系统i传递到子系统j的单向功率流;ηij为从子系统i到子系统j时的耦合损耗因子,其可以衡量两个子系统之间耦合程度强弱。对于线连接的两板子系统间的耦合损耗因子有 (4) 式中:l为板子系统间线连接长度;Cg为子系统的群速度;Ai为子系统i的表面积;ω为频带中心频率;τij为传递系数,可用经验近似公式计算[21]。 已知外界对子系统i的输入功率为Pi,in,对于N个相互耦合的SEA子系统,第i个子系统的功率平衡方程[22]有 (5) 在保守耦合的条件下,对于线性、无源和可逆子系统构成的大系统,根据互异性原理有 ni(ω)ηij=nj(ω)ηji (6) 则功率平衡方程可表达为矩阵形式 {Pin}=ω·[L]·{E} (7) 其中 (8) 式中:ρ0为空气密度;c为声波在空气中的传播速度;σi为板子系统的声辐射效率;Si为板件表面积。 1.3.1 列车-轨道-桥梁耦合频域模型 车辆子系统由1/8车体、1/4转向架、车轮、一系悬挂、二系悬挂组成,如图1所示。Ma为1/8车体+1/4转向架质量;K1,C1为一系悬挂刚度及阻尼;Mw为单个轮对质量;Kc为轮轨接触刚度。由于二系悬挂自振频率约1 Hz,小于本文分析频率,其在进行动力计算时可忽略不计。 图1 列车-轨道-桥梁耦合频域模型Fig.1 Vehicle-track-bridge coupling frequency-domain model 为了使数值模拟结果与现场试验结果形成有效对比,本文采用与千厮门大桥一致的减振垫浮置板轨道结构,如图2所示。将钢轨简化为无限长度的Timoshenko梁,将轨道板简化为等长度节段的Euler梁,将减振垫和轨道扣件简化为离散均布的竖向支撑弹簧。 图2 减振垫浮置板示意图Fig.2 Damping pad-floating slab track structure diagram 1.3.2 基于移动不平顺模型的动态轮轨力 列车过桥时,轮轨接触面不平顺引起的小幅度波动会导致轮-轨接触系统产生位移激励,即轮轨相互作用力。本文基于移动不平顺模型,考虑车轮动柔度、钢轨动柔度以及轮轨接触动柔度三者的相互影响,计算该动态轮轨力[23] (9) 式中:Δ为考虑了时间滞后效应的轨道不平顺谱;αw,αc,αr分别为车轮动柔度、钢轨动柔度以及轮轨接触动柔度,其中αc=1/Kc。 根据达朗贝尔原理,车轮动柔度可由式(10)计算 (10) 式中:K0为有限元法计算得到的列车模态刚度的动力响应曲线的最低点的值;η0为列车模态刚度的动力响应曲线最低点处相对应的损失因子;i为复数单位。 1.3.3 多轮对作用下的钢轨动柔度计算模型 在多轮对作用条件下,钢轨的动柔度αr可由模态叠加法求解。即假设所有轮对均与钢轨接触,但仅考虑第j组轮对与轨道的接触粗糙度,称其为“主动轮”,其余未考虑接触粗糙度的称为“被动轮”,如图1所示。由于不同轮对在钢轨上作用位置的差异,考虑轮轨力引起的振动波在传递过程中的衰减,根据振动波的叠加效应,在多组轮对作用条件下,列车第组轮对作用位置处的钢轨动柔度可由式(11)计算 (11) 式中:α(x1,x2)为在轨道上沿桥向在x2点作用单位力时x1点的位移响应函数,该函数可由无限长的Timoshenko梁模型的运动偏微分方程得出;α(0,0)为钢轨的初始动柔度值;NT为轨道板的个数;NP为单块轨道板对应的扣件个数;Fpn,xn为第n个扣件的扣件力及对应的x坐标;Fwm,xm为第m组被动轮的轮轨接触力及对应的x坐标。扣件力Fpn、轮轨接触力Fwm的计算参考王党雄等的研究。 根据移动不平顺模型,多轮对作用下不同轮对的轨道不平顺存在滞后效应,同一列车第1组~第4组轮对的轨道不平顺激励可表示为 (12) 式中:L1,L2为车轮间距;v为列车运行速度。 基于1.1节~1.3节理论建立钢桁梁的SEA预测模型,如图3所示。主要构件包括上下层桥面系的桥面板、横梁、纵梁以及两侧主桁架的上下弦杆和斜杆的腹板。列车荷载以等效频谱力的形式作用在下层桥面板子系统上。 图3 钢桁梁SEA噪声预测模型Fig.3 SEA noise production model of steel truss bridge 结构内损耗因子ηi取决于结构本身的阻尼特性 ηi=ηis+ηir+ηib (13) 式中:ηis为结构子系统本身材料内摩擦构成的损耗因子;ηir为结构子系统振动声辐射阻尼形成的损耗因子;ηib为结构子系统边界连接形成的损耗因子。但对于钢结构子系统,其内损耗因子通常受材料内摩擦形成的结构损耗因子ηis的支配,因此本文中钢结构子系统的内损耗因子取0.1%[24]。 由于板子系统的振动模态以面内弯曲为主,其面内伸缩波和剪切波的模态密度远小于弯曲波,因而本文仅考虑弯曲波的声振效应。如图4所示为钢桁梁下层桥面板、纵梁腹板、横梁腹板以及斜杆腹板子系统的弯曲模态数,可见其在本文的分析频段内基本上位于中高频区,满足统计能量分析的基本要求。主要声辐射构件的模态重叠因子,在分析频段内均满足计算要求,如图5所示。 图4 钢桁梁主要构件模态数Fig.4 The model number of steel truss bridge 图5 钢桁梁主要构件模态重叠因子Fig.5 The model overlap factor of steel truss bridge 为了进行有效对比,本文基于相同的理论建立了与千厮门大桥体量相当的钢箱梁桥模型,其SEA模型如图6所示。基本构件包括钢桥面板、横隔板、边腹板、中腹板、纵肋、底板。桥面板和横隔板的弯曲模态数和模态重叠因子,均满足分析要求,如图7、图8所示。 图6 钢箱梁SEA噪声预测模型Fig.6 SEA noise production model of steel box-girder bridge 图7 钢箱梁主要构件模态数Fig.7 The model number of steel box-girder bridge 图8 钢箱梁主要构件模态重叠因子Fig.8 The model overlap factor of steel box-girder bridge 本文针对重庆千厮门嘉陵江大桥开展现场试验。千厮门大桥为一座单塔单索面公轨两用双层钢桁梁斜拉桥,主桥全长720 m,主跨312 m,桁宽15 m,采用减振垫浮置板轨道结构,立面、横截面示意图如图9、图10所示。车辆、轨道的具体参数参考Liang等的研究。为了降低轮轨噪声等其他桥面上部对梁体车致振动结构噪声现场实测数据的影响,在主跨跨中断面布置噪声测点,如图11所示。S-1,S-2,S-3分别为第一孔、第二孔、第三孔横梁腹板跨中。由于桥面板自身对桥面上方各类噪声的遮蔽效应,可将S-1,S-2,S-3测点的噪声视为近场结构噪声。 图9 千厮门大桥主桥立面示意图(m)Fig.9 Elevation diagram of main bridge of Qiansimen (m) 图10 千厮门大桥横截面示意图(mm)Fig.10 Cross section diagram of Qiansimen Bridge (mm) 图11 跨中断面测点布置图Fig.11 Arrangement of measuring points on mid-span cross section 本次试验的噪声传感器为MPA231型噪声测试麦克风,数据采集设备为INV3060S型24位智能采集仪,如图12所示。现场试验情况如图13所示。 图12 主要试验设备Fig.12 Main test equipment 图13 千厮门大桥现场试验情况Fig.13 On-site experiment of Qiansimen Bridge 经现场测试,列车通过测试断面的行驶速度为50 km/h,因而本文的列车荷载均采用50 km/h的速度。将S-1,S-2,S-3 3个测点在近轨、远轨工况下的A计权声压级在16~6 300 Hz分析频段的分布规律以及总声级与3次现场测试数据进行对比,如图14、图15所示。为了避免桥上汽车、桥下船舶、自然风等因素对噪声采集的干扰,本试验每组工况的每个测点均进行了背景噪声采集。图14、图15所示试验数据均为排除背景噪声干扰后的结果。 图14 测点实测噪声值与预测值的频域分布对比Fig.14 Comparison of testing and producing noise values of field points in frequency domain 图15 测点实测噪声与数值模拟结果总声级对比Fig.15 Comparison of testing and producing total sound pressure level of field points 由图14、图15可知:钢桁梁桥桥面板下方横梁不同跨腹板中心处的桥梁结构噪声辐射在频域上的分布规律基本一致,呈宽频特性,噪声峰值均分布在63~200 Hz内。3个测点的仿真曲线在频域上的分布规律与现场试验结果在全频段基本一致,尤其是在16~2 500 Hz内。SEA模型预测的总声级略小于实测结果,主要是由于本文建立的SEA模型与现实条件还存在差异,如没有考虑板件、大地等构件和环境的声反射效应等。 综上分析,本文建立的SEA噪声预测模型在频域上的分布规律和总声级与实测结果基本吻合,可用于后续对大跨度钢桁梁、钢箱梁结构噪声特性的研究。 为了对大跨度钢桁梁、钢箱梁桥的远场结构噪声辐射规律进行对比,本节选取了5个噪声分析场点,如图16所示。M1为钢桁梁模型,M2为钢箱梁模型。S1,S2为近轨轨道中心线垂下方5 m,10 m处场点,S3,S4,S5为列车行车水平面上距近轨轨道中心线水平距离7.5 m,25.0 m,50.0 m场点。 图16 桥梁结构噪声场点布置图(m)Fig.16 Arrangement of field points of structure-borne noise (m) 在50 km/h列车荷载和相同的轨道结构参数作用下,钢桁梁、钢箱梁桥在S-1~S-5场点的辐射结构噪声在频域内的分布曲线,如图17所示。A计权总声压级以及两者的差值,如图18所示。 图17 钢桁梁、钢箱梁桥在S-1~S-5场点的结构噪声辐射Fig.17 The structural noise radiation of steel truss bridge and box-girder bridge at S-1 to S-5 field points 图18 钢桁梁、钢箱梁在S-1~S-5场点总声压级及差值Fig.18 The total sound pressure level of steel truss and box-girder bridge and difference value at S-1 to S-5 points 钢桁梁、钢箱梁桥的结构噪声均呈宽频分布特性,峰值频率均集中在63~160 Hz频段内,这是由于两者在相同荷载激励作用下,传递到桥梁结构的力主导频率一致,如图17所示。此外,钢箱梁在800~1 000 Hz频段内也表现出较突出的峰值。 在垂直和水平方向,均随着离轨道中心线距离的增大,钢桁梁、钢箱梁桥在场点的结构噪声辐射逐渐减小,如图18所示。在行车中心线的正下方5 m,10 m处,钢桁梁的总声级比钢箱梁分别小1.6 dB(A)和1.0 dB(A);在距轨道中心线水平距离7.5 m,25.0 m,50.0 m处,钢桁梁辐射的结构噪声值要略大于钢箱梁,且该差值随着距离的增大而增大,这是由于两者不同频段噪声成分的比例不同。 为分析两种结构桥梁的远场结构噪声辐射规律,以近轨中心线为原点,作出桥梁跨中截面在水平距离(0.75,50.00)m,垂直距离(-10,15)m内的A计权声压级云图,如图19所示。 图19 钢桁梁、钢箱梁桥跨中截面A计权声压级云图Fig.19 The A-weighted sound pressure level of steel truss and box-girder bridge at mid-span section 由图19可知:钢桁梁、钢箱梁结构噪声等压线在跨中横断面均呈半弧形分布。两者结构噪声在行车中心线水平面上的衰减率,如表1所示。可见在小于15 m的距离范围内,钢桁梁的衰减速率小于钢箱梁,而在大于15 m的距离范围内则相反。由于具有更小的梁高,在垂直方向上钢箱梁的等压线分布更加密集,即衰减率更大。 表1 钢桁梁、钢箱梁水平方向结构噪声衰减率Tab.1 Attenuation rates of horizontal structural noise of steel truss and box-girder bridge 为了讨论钢桁梁、钢箱梁桥不同构件对场点总声压级的影响,本文对两者不同构件在S4(25,0)和S2(0,-10)场点处的声贡献量进行了分析,如图20~图25所示。 图20 钢桁梁桥不同构件在S4,S2的辐射声压值Fig.20 Components’radiation rates of steel truss bridge on points S4 and S2 图21 钢桁梁不同构件在S4的声贡献量Fig.21 Components’acoustic contribution of steel truss bridge on point S4 图22 钢桁梁不同构件在S2的声贡献量Fig.22 Components’acoustic contribution of steel truss bridge on point S2 图23 钢箱梁桥不同构件在S4,S2的辐射声压值Fig.23 Components’radiation rates of steel box-girder bridge on points S4 and S2 图24 钢箱梁不同构件在S4的声贡献量Fig.24 Components’acoustic contribution of steel box-girder bridge on point S4 图25 钢箱梁不同构件在S2的声贡献量Fig.25 Components’acoustic contribution of steel box-girder bridge on point S2 由图23~图25可知:钢箱梁的主要声辐射构件为桥面板,其在水平方向测点的声贡献可达31.38%,在垂直下方测点的声贡献可达46.04%。钢箱梁各构件对P1,P2场点声辐射值大小的规律均为:“桥面板”≫“横隔板”≈“边腹板”≫“纵肋”≈“中腹板”>“底板”。 由图20~图22可知:钢桁梁各构件对S4,S2场点声辐射值大小的规律为:“下层桥面系”≫“近主桁”>“上层桥面系”>“远主桁”,即钢桁梁的远场结构噪声辐射主要构件为下层桥面系,其对S4,S2场点总声级的贡献量可达79.40%和90.96%,其中桥面板的声贡献量为32.08%和35.47%。此外,不同构件对不同方位的场点的辐射能力也不相同。钢桁梁上层桥面系和近主桁在行车面水平方向(S4)的声贡献比例要大于在垂直下方(S2)的声贡献比例,而下层桥面系各构件和远主桁则相反,这与构件在空间上与场点的相对位置和板件的主要辐射面的朝向有关。 (1)本文以列车-轨道-桥梁耦合频域分析计算出的频谱力为激励,建立了大跨度钢桥的SEA结构噪声预测模型,并以千厮门大桥的现场试验结果验证了上述模型的合理和可靠性,尤其在16~2 500 Hz频段。该模型可用于大跨度钢桥全频段结构噪声特性分析。 (2)大跨度钢桥的结构噪声主要分布在中、高频段,呈宽频分布特性,峰值集中在63~160 Hz,而钢箱梁在800~1 000 Hz频段内也表现出较突出的峰值。 (3)大跨度的钢桁梁、钢箱梁桥相比,在行车中心线的正下方5 m,10 m处,钢桁梁的总声级比钢箱梁分别降低1.6 dB(A)和1.0 dB(A);而在距轨道中心线水平方向上,钢桁梁结构噪声略大于钢箱梁;且钢桁梁与钢箱梁总声级的差值随着距离的增大而增大。 (4)钢桁梁的主要声辐射结构为由下层桥面板、横梁、纵肋、下弦杆组成的下层桥面系,其在水平和垂直方向测点的声贡献可达79.40%和90.96%,其中桥面板的声贡献量最大,可达32.08%和35.47%,纵梁、下弦杆、横梁仅次之。钢箱梁的主要声辐射构件为桥面板,其在水平方向和垂直方向测点的声贡献可达31.38%和46.04%,其次是横隔板和边腹板,纵肋、中腹板和底板的声贡献量远小于前者。1.2 SEA功率平衡方程

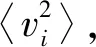
1.3 输入激励
1.4 大跨度钢桥的SEA噪声预测模型
2 现场试验验证
2.1 试验概况


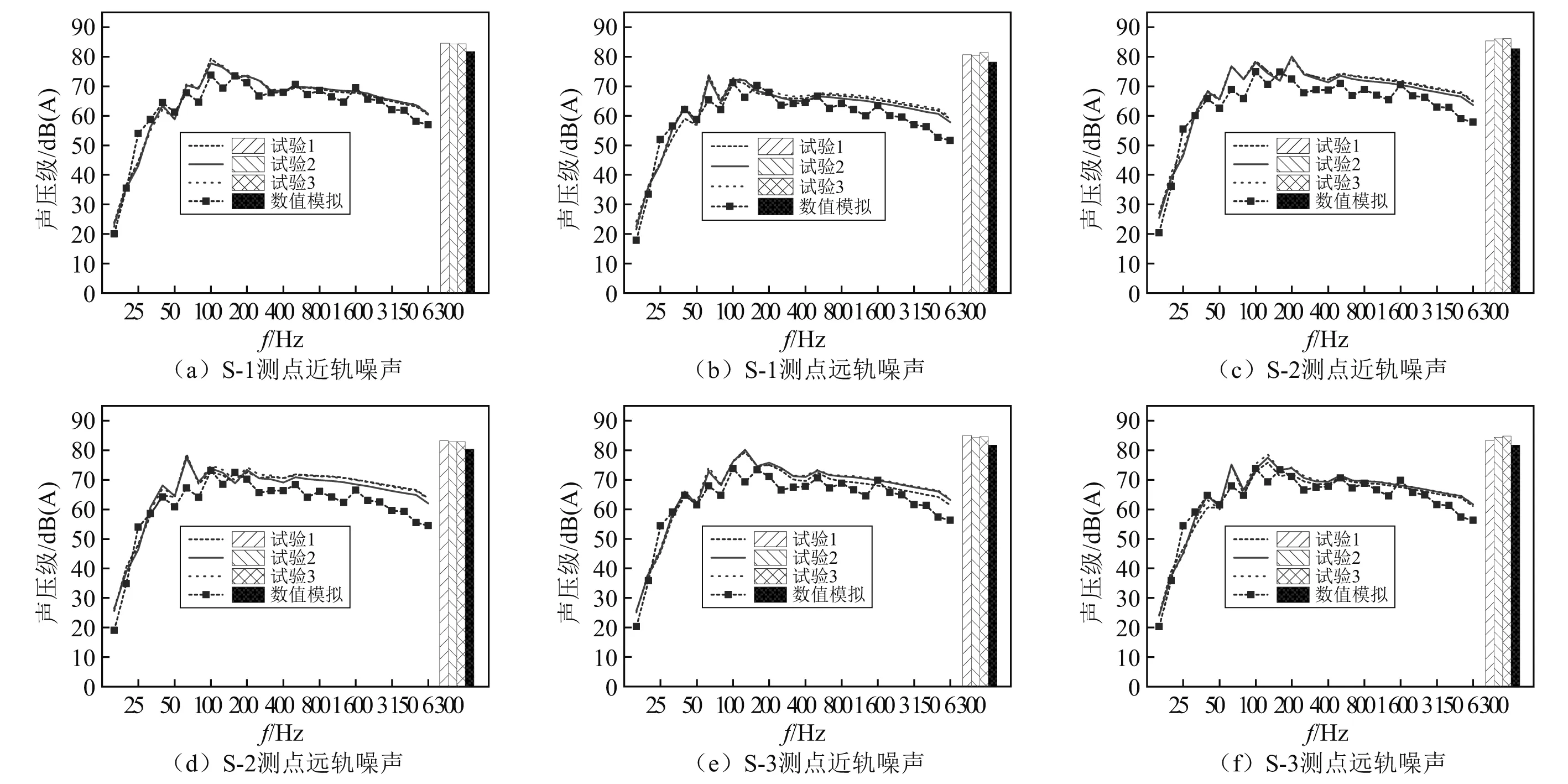
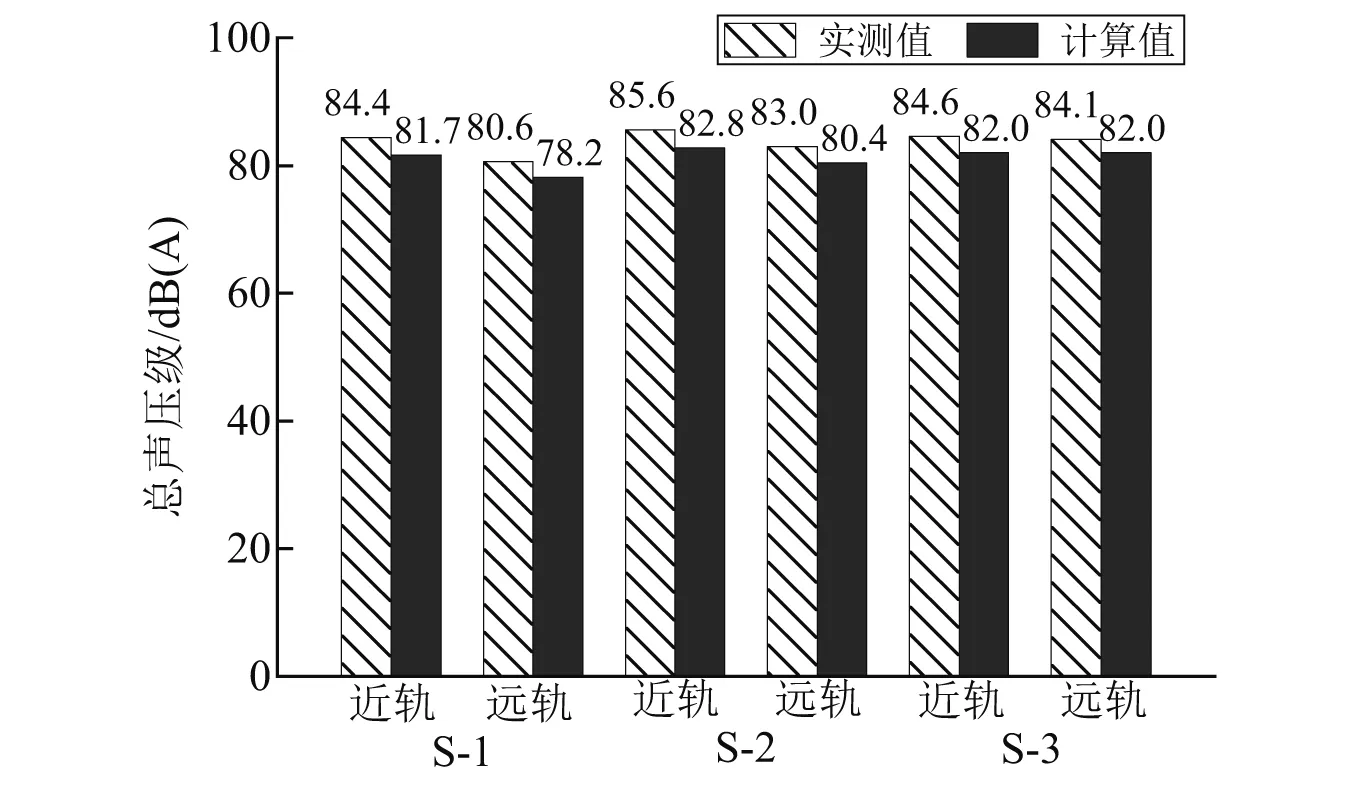
2.2 试验数据与仿真结果对比
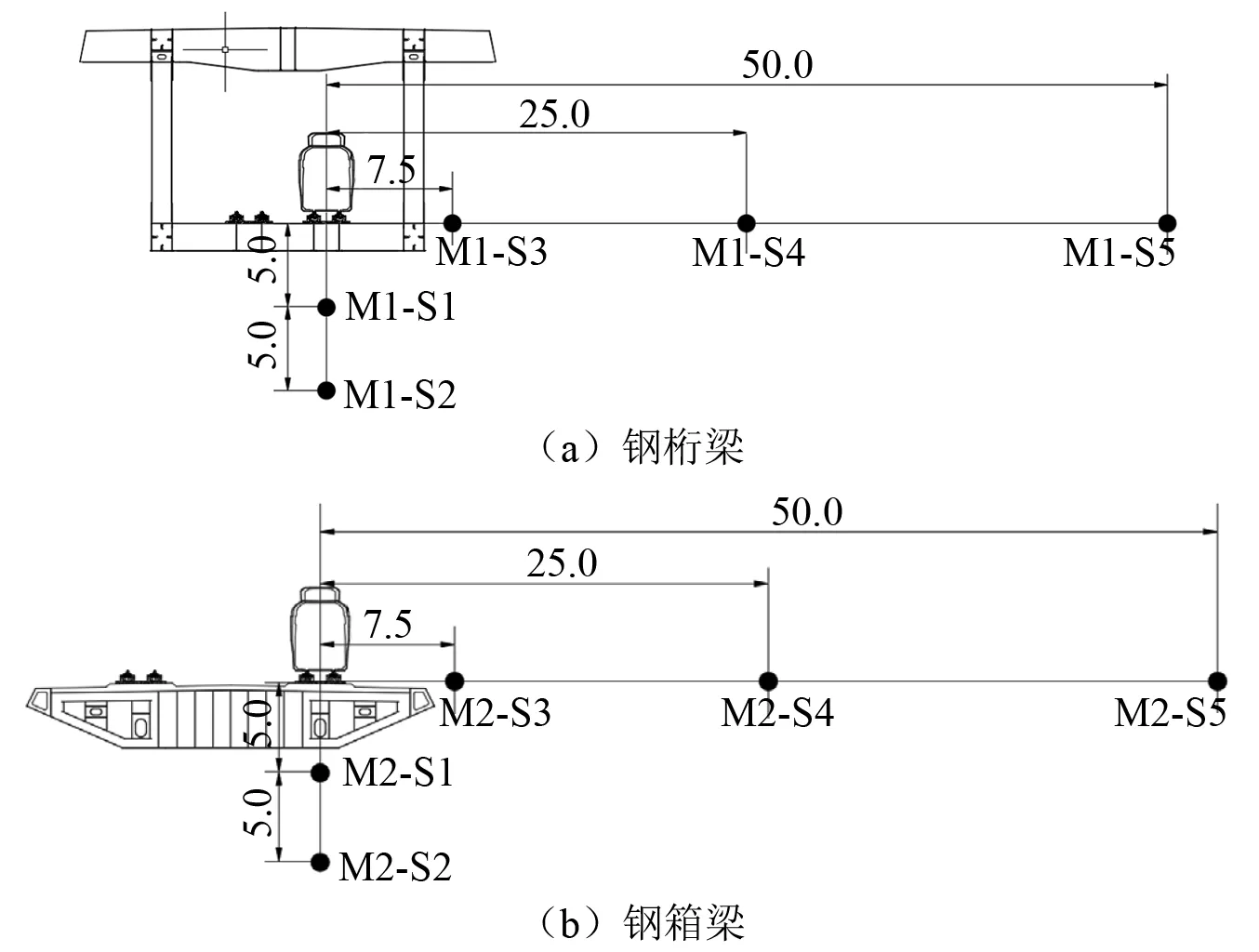
3 钢桁梁、钢箱梁桥的结构噪声特性对比
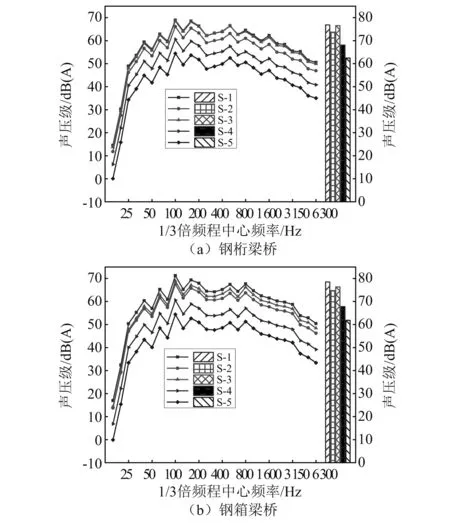
3.1 结构噪声辐射及衰减规律

3.2 构件声贡献量分析
4 结 论
