基于gPC理论的不确定参数电动汽车脉冲响应研究

田国英，张大伟，易兴利，邓鹏毅，孙树磊

(1.西华大学 汽车与交通学院，成都 610039；2.西华大学 汽车测控与安全四川省重点实验室，成都 610039；3.西华大学 四川省新能源汽车智能控制与仿真测试技术工程研究中心，成都 610039；4.长安大学 汽车学院，西安 710064；5.中车株洲电力机车有限公司，湖南 株洲 412001)

平顺性是评价汽车性能的主要指标之一，其优劣对乘坐舒适性、零部件及路面的疲劳寿命和行驶安全性均有重要影响，如何提高平顺性一直受到整车厂、各国研究机构和学者的重视[1-2]。

目前，汽车平顺性动力学方面的相关研究已经取得了很大发展，但是，多数研究仍基于车辆结构参数为确定性的动力学模型[3-6]。汽车平顺性随机振动研究中主要以平稳高斯随机路面不平作为输入，较少考虑参数不确定的影响。实际上，受生产制造、长期运营磨损老化及运载条件变化等因素影响，车辆自身结构参数相对于设计值是随机变化的，在研究汽车平顺性时有必要考虑参数不确定的影响。考虑参数不确定的汽车动力学计算方法主要有蒙特卡洛(Monte Carlo，MC)法[7]、协方差法[8]、区间法[9]及广义多项式混沌(generalized polynomial chaos，gPC)法[10]等。其中，MC法计算效率较低，协方差法仅能给出响应的统计值，区间法则需确定参数的具体范围，但汽车大多数结构参数的分布范围并不明确。

gPC法能有效缓解上述问题，近年来发展迅速。该方法源于Wiener[11]的均匀混沌理论，他最早给出用埃尔米特正交多项式组合描述高斯随机过程的表达式。此后，Ghanem等[12]将该方法与有限元法结合，并在结构动力学领域开展了大量研究。在此基础上，Xiu等[13-14]基于Askey框架，将埃尔米特多项式表示高斯随机过程的方式拓展到其他随机过程的正交多项式混沌展开，建立了正交多项式和多数概率分布间的对应关系，扩展为广义多项式混沌理论。Sandu等[15-16]最早将gPC理论引入多体系统动力学和汽车动力学中，其研究团队开展了包括汽车垂向动力学[17]、胎地相互作用[18]、操纵稳定性[19]等方面的不确定参数随机振动分析。之后，学者们利用gPC理论在汽车及其零部件参激随机振动方面开展了较多工作[20-24]。与汽车平顺性相关的研究主要有：Sandu等建立了悬架刚度和阻尼非线性的1/4汽车垂向模型，通过计算不确定悬架阻尼、轮胎刚度和路面不平下的振动响应，与MC法对比，说明了gPC方法计算的准确性和高效性。Li等建立7自由度越野车辆动力学模型，分析了轻/重车情况下不确定结构参数和土壤湿度对车辆牵引能力的影响。Kewlani等借助1/4车辆垂向模型对比了gPC法、多元gPC法和MC法的差异，从理论和实验两方面验证了gPC方法的正确性。凌锋利用Adams/Car软件建立某型汽车整车模型，与MATLAB软件联合仿真悬架刚度和阻尼不确定时的动力学响应统计值，与MC法对比验证了PC法的正确性。Wu等提出了一种多项式混沌-切比雪夫区间的混合方法，以4自由度汽车垂向模型为例，验证了方法在计算不确定参数影响中的准确性和高效性。上述工作已经证明了gPC理论在汽车动力学分析中的可行性和计算精度，但这些研究侧重方法准确性的验证，且其汽车平顺性模型做了大量简化，缺乏参数不确定对汽车平顺性的影响程度及规律的研究。因此，基于gPC理论，在以往理论方法可行性及准确性验证基础上，利用完整汽车平顺性模型，从工程应用角度开展关键参数不确定的定量影响研究显得十分必要，可为合理预测汽车平顺性响应范围，并对关键零部件的设计和可靠性评估提供帮助。

本文将gPC理论运用于汽车平顺性分析中，建立考虑电机参振的含不确定参数电动汽车的平顺性模型。在与MC法对比验证基础上，分别在整车和电机总成两类参数不确定条件下，对某型电动乘用车以不同车速通过脉冲型路面时的平顺性和电机振动响应的统计指标开展细致的分析工作，获得参数不确定对各个振动响应的影响规律和定量化程度，以期为汽车平顺性方面的参激随机振动分析提供参考。

1 基于gPC理论的不确定参数电动汽车平顺性模型

1.1 考虑电机参振的电动汽车平顺性模型

考虑电机参振的电动汽车平顺性模型，如图1所示。模型中，假设车体、人体、电机和车轮均为刚体。车体由4个悬架共同支撑，考虑垂向(Zb)、俯仰(βb)和侧倾(Φb)运动3个自由度；电机通过3个悬置弹性连接至车体前部，考虑垂向(Ze)、俯仰(βe)和侧倾(Φe)运动3个自由度；人体和车轮仅考虑垂向运动(Zp和Zw)，共计11个自由度。图1中：Mb，Mp，Me和Mw分别为车体、人体、电机和车轮质量；Ibx，Iby分别为车体侧倾和俯仰惯量；Iex和Iey分别为电机侧倾和俯仰惯量；Ks和Cs分别为悬架弹簧刚度和减振器阻尼；Kc和Cc分别为座椅刚度和阻尼；Kt为轮胎垂向刚度；Km和Cm分别为电机悬置垂向刚度和阻尼；Lfc和Lrc分别为质心距前轴和后轴的距离；Wf和Wr分别为前轴和后轴的轮距；其他尺寸参数如附录A所示；Z0为路面不平度输入。

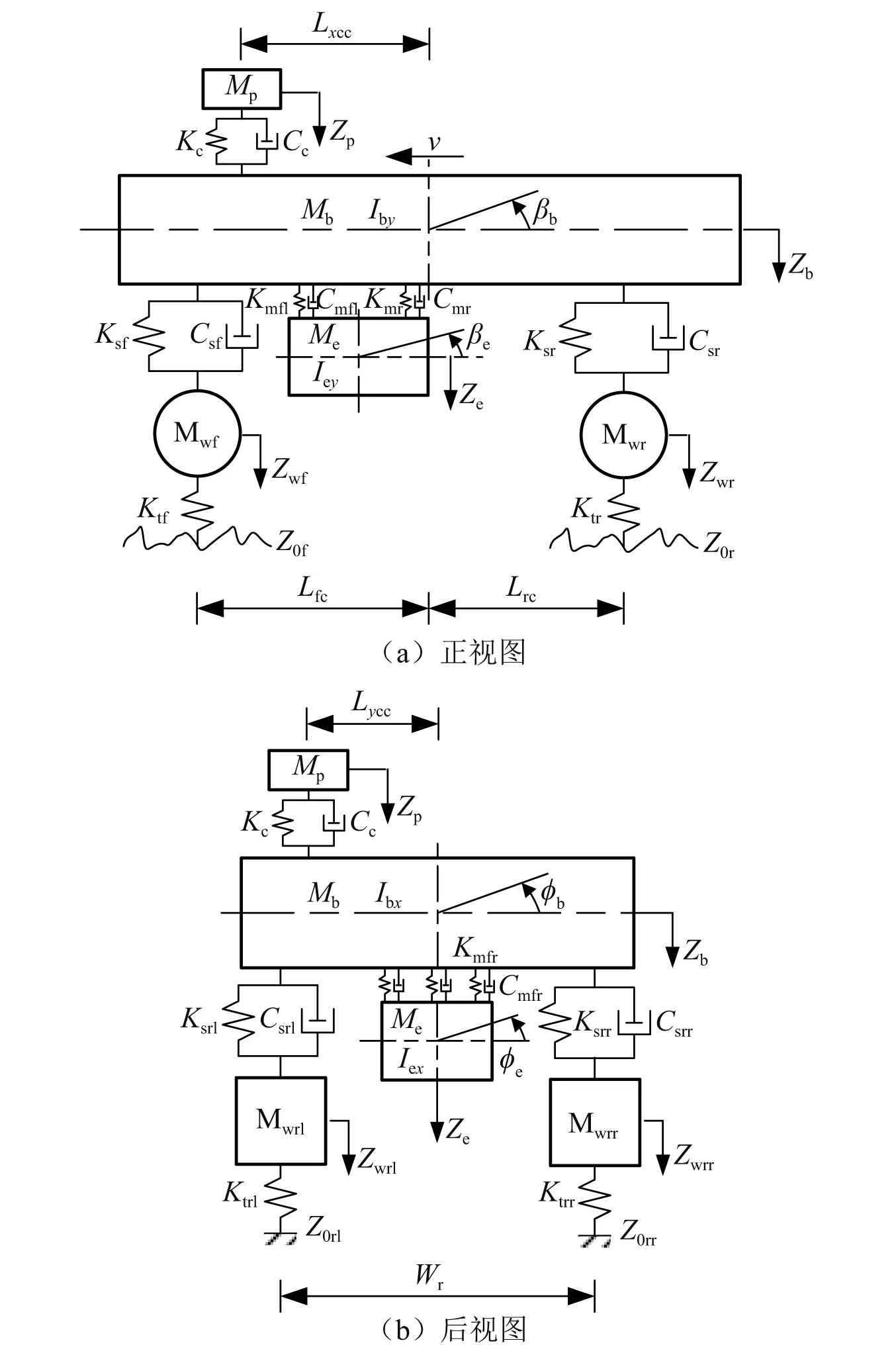
图1 考虑电机参振的电动汽车平顺性模型Fig.1 Vertical dynamics model of an electric vehicle considering electric motor vibration

根据牛顿第二定律和车辆各部件受力分析，可得各自由度的动力学方程

(1)车体垂直运动

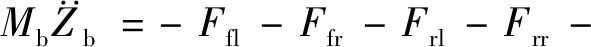
(1)

(2)车体俯仰运动

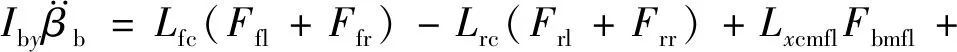
(2)

(3)车体侧倾运动

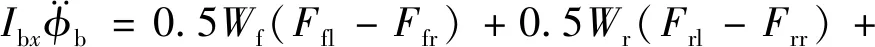
(3)

(4)电机垂向运动

(4)

(5)电机俯仰运动

(5)

式中，Te为电机驱动扭矩，根据汽车驱动理论[25]，可得

式中：G为整车重力；f为滚动阻力系数；α为坡度角；CD为空气阻力系数；A为迎风面积；v为车速；δ为旋转质量换算系数；r为车轮半径；iz为传动系总传动比；ηt为传动系传动效率。根据上式可计算不同车速、坡度和加速条件下的电机驱动扭矩，进而影响电机俯仰振动。

(6)电机侧倾运动

(6)

(7)人体垂向运动

(7)

(8)左前车轮垂向运动

(8)

(9)右前车轮垂向运动

(9)

(10)左后车轮垂向运动

(10)

(11)右后车轮垂向运动

(11)

式中：Ffl,Ffr,Frl,Frr为4个悬架垂向作用力；Fbm为车体对电机的垂向作用力；Fpb为座椅对车体的垂向作用力；Ft为车轮与路面作用力；以上各作用力的具体表达式可通过受力分析获得，此处不再赘述。为真实模拟车轮与路面相互作用，考虑了当轮胎上跳过大时可能出现车轮跳离地面的情况，因此，车轮与路面作用力可表达为

(12)

1.2 广义多项式混沌理论的应用

目前，基于gPC理论的计算方法主要有两种，随机伽辽金方法(stochastic Galerkin method,SGM)和随机配点法(stochastic collocation method,SCM)。由于随机伽辽金方法需要对原确定性模型进行不确定变量的混沌展开推导，工作量大，且不同的不确定变量需重新推导，不利于快速建模和计算，故随机伽辽金方法一般用于自由度不大的简单模型。相比之下，随机配点法无需对原确定性模型进行修改，只需将原模型封装成子程序开展计算，大大简化了复杂模型的随机分析工作。因此，本文利用随机配点法开展不确定参数的影响计算。

对于式(1)～式(11)的各部件动力学方程，其系统动力学方程可总体表达为

(13)

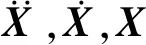
当考虑系统存在参数不确定时，式(13)可变形为

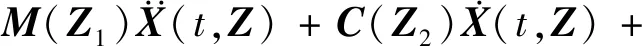
(14)

式中：Z为总不确定参数向量；Z1，Z2，Z3和Z4分别为对应质量、阻尼、刚度和外部激励的不确定参数向量，可展开表达为

(15)

式中，D1，D2，D3和D4分别为对应质量、阻尼、刚度和外部激励的不确定参数数量，记不确定参数总数D=D1+D2+D3+D4。

根据gPC理论，各类不确定参数可表达为多项式混沌展开形式，即

(16)

(17)

(18)

(19)

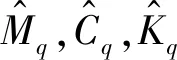
类似的，系统输出响应也可表达为多项式混沌展开形式

(20)

(21)

(22)

式中：i=(i1,…,ij,…,iD)，j=1,…,D，为按正交多项式阶数的分级词典顺序排列的多重指标，ij为第j个随机变量的多项式阶数，|i|=i1+…+iD为其指标值；Φi(Z)为不同组合下各不确定参数正交多项式的乘积，即

Φi(Z)=φi1(Z11)…φiD(Z4D4)

(23)

H为D个不确定参数的多项式组合数，记Q=max(Q1,Q2,Q3,Q4)，则

(24)

对于随机伽辽金法来说，其通过将式(16)～式(22)代入式(14)，把原确定性方程组在随机域扩维后获得一组新的包含不确定参数的方程组，从而开展计算，其对复杂动力学系统的推导过程繁琐耗时。随机配点法则首先在式(15)构成的随机空间中选取节点，节点的选取依据高斯求积法则确定，设选取的节点集为ΘN={Z(n)}，N=N1×…×Nj×…×ND为节点集总数，Nj为第j个不确定参数的节点数，n=1,…,N。将ΘN代入式(16)～式(19)，进一步代入式(14)可得

(25)

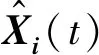
(26)

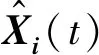
(27)

(28)

此外，为获得较准确的响应概率密度及分布，可通过对式(20)～式(22)中的不确定参数向量Z进行抽样得到响应的大样本数据，然后拟合获得其概率密度及相关概率统计；响应的变异系数εX可利用μX和σX的比值计算

(29)

2 不确定参数对电动汽车平顺性的影响分析

2.1 不确定参数的选取

针对所建立的电动汽车平顺性模型，以某型电动乘用车为例，将待分析的不确定参数分为两种工况：一种是对汽车平顺性有重要影响的整车参数；另一种是对电机振动有重要影响的电机总成参数，不确定参数的选取情况，如表1所示。

表1 不确定参数的选取Tab.1 Selection of uncertain parameters

从表1可知：在整车平顺性的主要影响参数中，考虑车体质量、悬架刚度和阻尼、轮胎刚度等4种参数随机变化。其中：考虑车辆运行中乘客Mp及行李质量Ml可能发生变化，且车体处于各种质量状态的概率并无差别，因此选取车体质量服从均匀分布，其上、下限分别为Mbu和Mbl，质量上限Mbu=Mb+4Mp+5Ml，Ml为每位乘客的行李质量，质量下限Mbl=Mb；其余不确定参数均服从正态分布，其均值取设计值，方差在均值的10%～30%。

在电机总成参数中，考虑电机质量、悬置刚度和阻尼等3种参数随机变化。其中，考虑到设计过程中电机选型的不同，且电机选型时处于各种质量状态的概率并无差别，因此选取电机质量服从均匀分布，其上、下限分别为Meu和Mel，分别取Meu=150%Me和Mel=50%Me；其余不确定参数服从正态分布，其均值取设计值，方差在均值的10%～30%。

此外，根据GB/T 4970—2009《汽车平顺性试验方法》规定，路面不平度选取典型的脉冲路面输入，其波形如图2所示。车速以10 km/h为间隔在10～60 km/h变化。

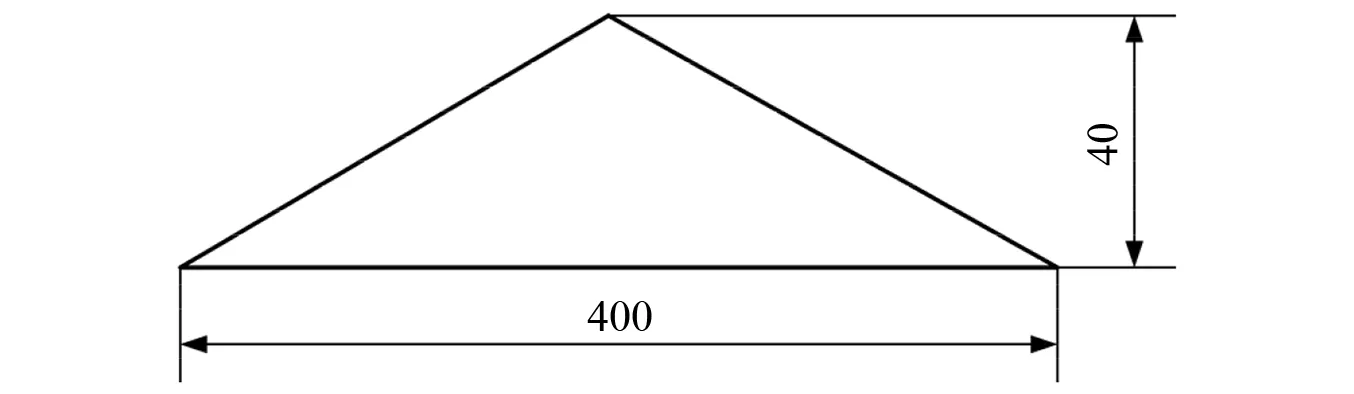
图2 脉冲型路面不平度输入(mm)Fig.2 Road impulse input (mm)

为验证基于SCM建立的不确定模型的正确性，在以上两类不确定参数工况下，将其与MC法的计算结果进行了对比，如图3和图4所示。计算中，车速取30 km/h，正态分布的不确定参数变异系数均取20%，MC法的样本数取10 000组。

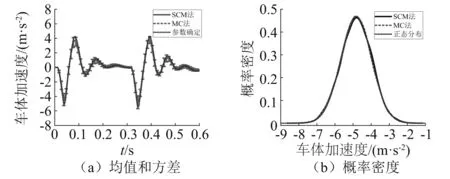
图3 车体加速度响应的对比Fig.3 Comparison of body acceleration responses

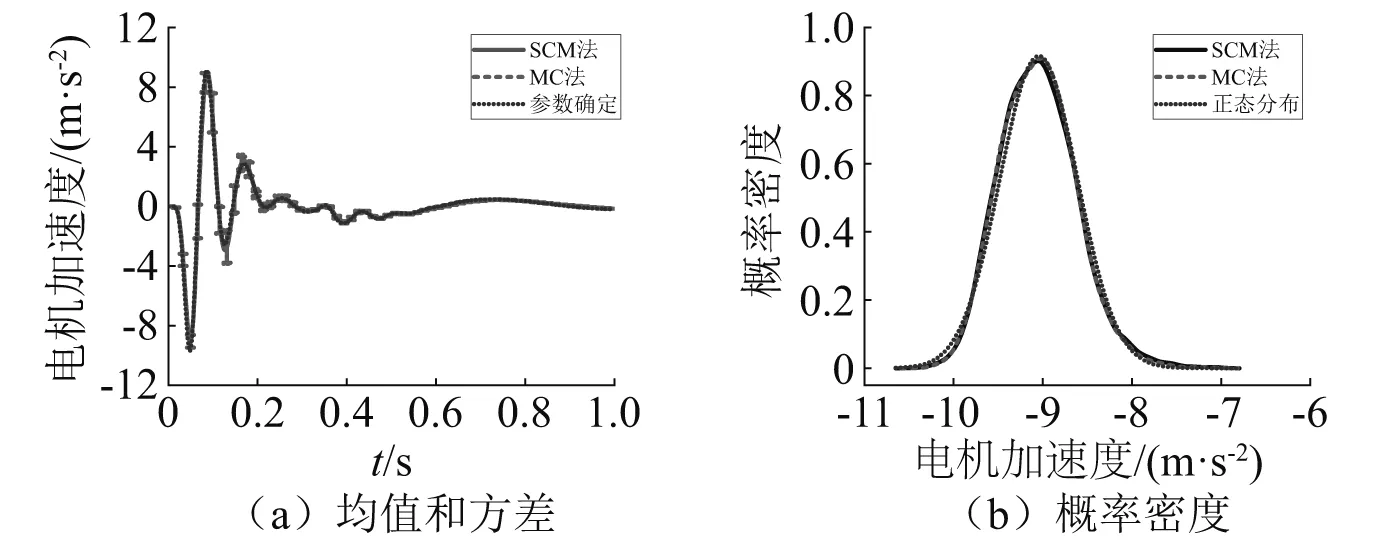
图4 电机加速度响应的对比Fig.4 Comparison of motor acceleration responses

由图3和图4可知：两种工况下，车体和电机加速度均值响应均与MC法计算结果完全重合，方差响应十分接近，响应最大值的概率密度曲线也几乎重合，从而说明了本文所建模型的正确性。此外，图中还给出了相应的确定性系统响应和标准正态分布的概率密度。可以看出，确定性系统响应与不确定系统响应在峰值位置处存在较明显差异，车体和电机加速度最大值的概率密度与标准正态分布较为接近。两种方法计算效率的对比数据，如表2所示。由表2可知：相比MC法，SCM利用较低的多项式阶数和较少组合数便可快速计算出准确结果，当不确定参数较少时，这一优势更为明显。

表2 SCM和MC法计算效率对比Tab.2 Comparison of computational efficiency between SCM and MC method

基于以上不确定参数选取和模型验证，下面分别在两种工况下对不确定参数对汽车平顺性的影响进行详细计算和分析，SCM的计算参数与表2相同。

2.2 整车参数对平顺性的影响(工况1)

根据表1，计算了工况1条件下的汽车平顺性响应，并进行了相关统计分析。60 km/h条件下，当正态分布的不确定参数变异系数均为30%时的车体和人体加速度、悬架压缩量和轮胎载荷的均值和方差响应，以及其概率密度随时间的演化特征，如图5所示。

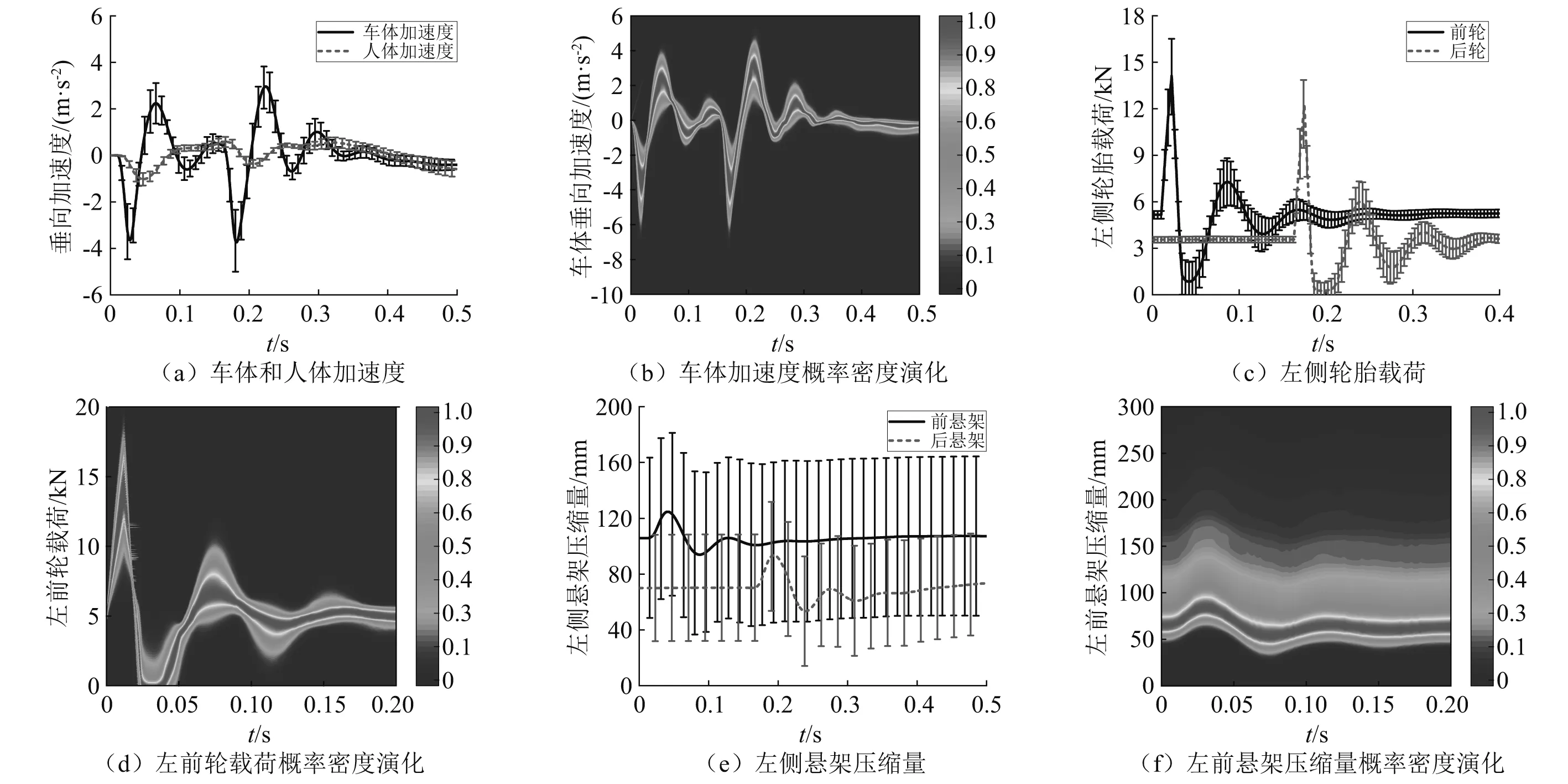
图5 整车参数不确定条件下的汽车平顺性响应Fig.5 Vertical dynamics responses under whole vehicle parametric uncertainties

由图5可知：不确定参数影响下各响应的动态分布范围清晰可见，在峰值处的方差较大。其中，悬架压缩量受参数不确定的影响较大，各时刻的响应方差均较大。由概率密度演化结果可明显看出大概率响应值的范围，车体加速度和轮胎载荷的大概率响应值基本分布在均值附近，而悬架压缩量的大概率响应值则与其均值有明显差异。也就是说，悬架压缩量的均值和方差不能完全表征参数不确定情况下的响应特征，还应结合概率密度演化来补充分析。

为细致考察输入变异系数和车速对各动力学响应的影响，各动力学均值响应最大值的变异系数随输入变异系数和车速的变化规律，如图6所示。一般来说，响应变异系数越大，说明不确定参数对该响应的影响越明显。

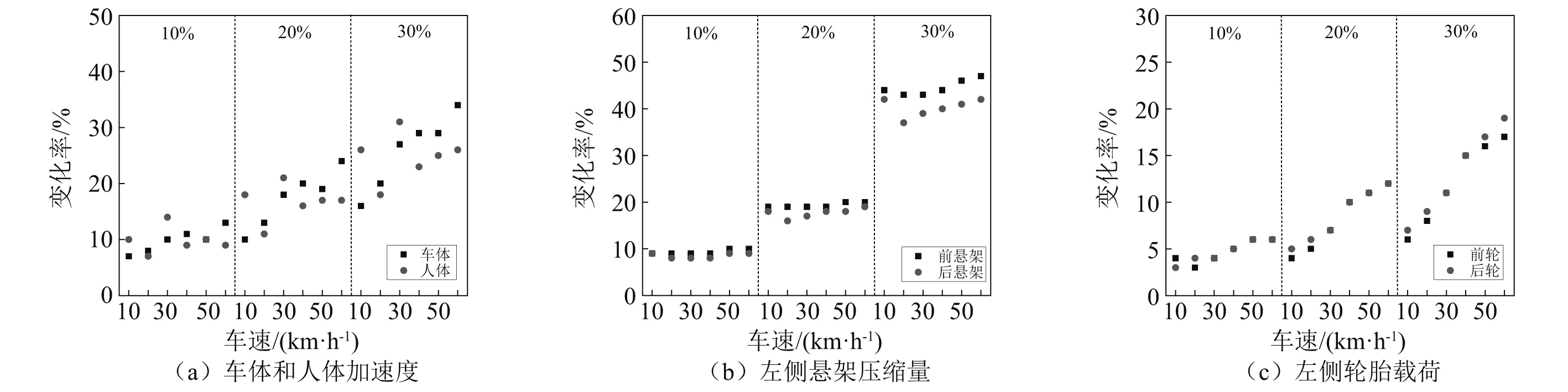
图6 平顺性响应最大值变异系数的变化规律Fig.6 Changing rules of variation coefficients for maximums of vertical dynamics responses

由图6可知：总体来看，随输入变异系数的增大，各响应的变异系数不断增大，且随车速提高，各响应的变异系数总体呈现增大趋势；悬架压缩量的变异系数最大，车体和人体加速度次之，轮胎载荷变异系数最小。具体来看，车体加速度变异系数较人体加速度大，二者最大可达34%和26%。前悬架压缩量的变异系数略大于后悬架，随输入变异系数增大，差别越明显；在不同输入变异系数下，悬架压缩量的最大变异系数分别为10%，20%和47%，响应变异系数甚至大于输入的变异系数；此外，车速对悬架压缩量响应的变异系数影响不显著。与悬架压缩量类似，前轮载荷的变异系数略大于后轮，但车速对轮胎载荷的变异系数影响较明显，尤其在大的输入变异系数情况下，几乎随车速提高线性增大；在不同输入变异系数下，轮胎载荷的最大变异系数分别为6%，12%和17%。

基于各响应最大值的概率密度，其分布范围、均值和方差随输入变异系数和车速的变化规律，如图7所示。

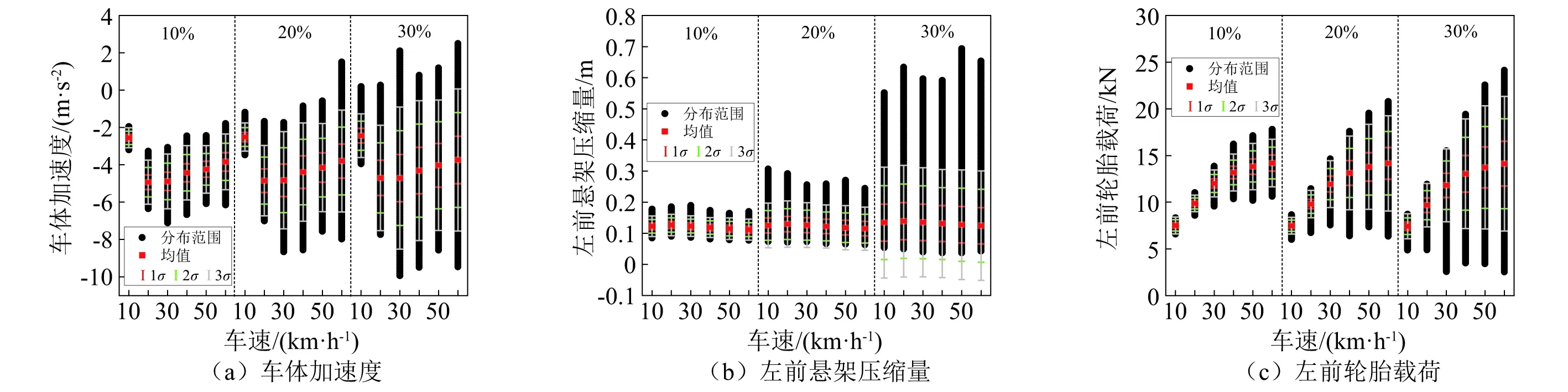
图7 平顺性响应最大值的均值、方差和分布范围变化规律Fig.7 Changing rules of means,variances and distribution ranges for maximums of vertical dynamics responses

由图7可知：总体来看，随输入变异系数增大，各响应最大值的均值变化不大，但其方差和分布范围均有明显提高，说明输入变异系数主要影响方差和分布范围，对均值影响不大。随车速提高，车体加速度和悬架压缩量最大值的均值总体略有下降，轮胎载荷则明显增大；车体加速度和轮胎载荷方差和分布范围总体不断增大，悬架压缩量则略有下降。

根据各动力学响应最大值的概率密度，图8给出其概率分布，并基于此计算了各动力学响应最大值超过设定阈值的概率。其中，车体加速度、悬架压缩量、轮胎最大载荷和最小动载的阈值分别设置为0.5g，0.14 m(悬架设计行程)、15.5 kN(3倍静轮载)和0(离地)。

由图8可知：总体来看，随输入变异系数的降低，各响应概率分布曲线越来越陡峭，这与前述的响应最大值的分布范围变窄一致。从超限概率来看，不同输入变异系数下车体加速度超过0.5g的最大概率分别为53%，47%和45%，随输入变异系数增大超限概率最大值略有下降；除10 km/h车速外，车体加速度超限概率总体随车速提高而降低，反映出在小变异系数和低速时的车体加速度最大值略微偏大；悬架压缩量超过设计值的最大概率分别为14%，29%和36%，随变异系数提高明显增大，相反随车速提高而降低，说明在大变异系数和低速时悬架压缩量较大；轮胎载荷最大值超过3倍静载的最大概率分别为8%，23%和30%，其超限概率随变异系数和车速提高均明显增大，说明在大变异系数和高速时的轮胎动载较高；轮胎载荷最小值离地最大概率分别为64%，54%和42%，除了车速10 km/h车轮不发生离地外，离地概率总体上随变异系数和车速提高而下降，说明在小变异系数和低速时车轮更容易与地面脱离。

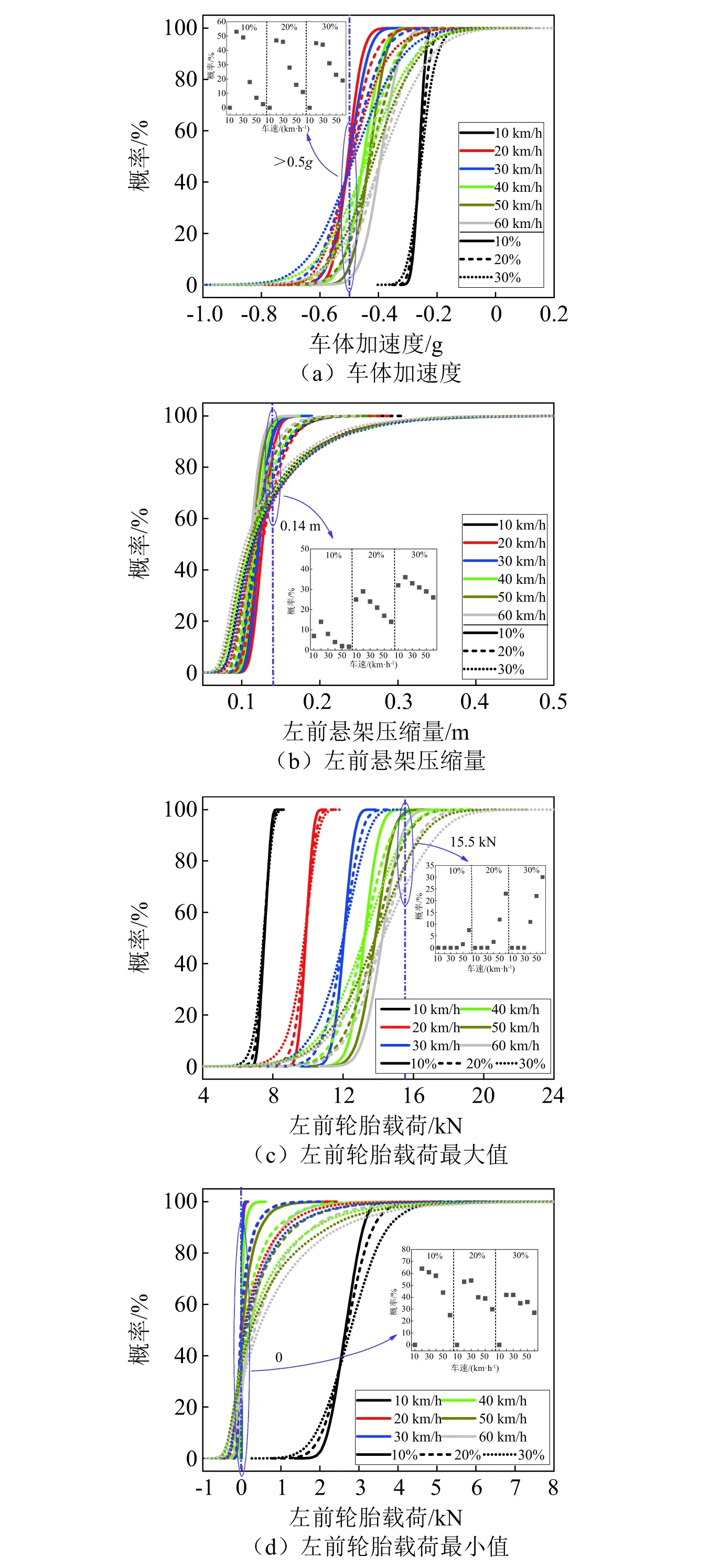
图8 平顺性响应最大值的概率分布及超限概率Fig.8 Probability distributions and overrun probabilities for maximums of vertical dynamics responses

2.3 电机总成参数对电机振动的影响(工况2)

根据表1，计算了工况2条件下的电机振动响应，并给出了相关统计分析。60 km/h条件下，当正态分布的不确定参数变异系数均为30%时的电机加速度和悬置压缩量的均值和方差响应，以及其概率密度随时间的演化特征，如图9所示。

图9 电机总成参数不确定条件下的电机振动响应Fig.9 Motor dynamics responses under motor assembly parametric uncertainties

由图9可知：不确定参数影响下各响应的动态分布范围清晰可见，在峰值处的方差较大。其中，电机悬置压缩量受参数不确定的影响较大，各时刻的响应方差均较大。由概率密度演化结果可明显看出大概率响应值的范围，电机加速度的大概率响应值基本分布在均值响应附近，而悬置压缩量的大概率响应值则与其均值有明显差异。同样，对于悬置压缩量来说，还应结合概率密度演化来补充分析参数不确定情况下的响应特征。

为细致考察输入变异系数和车速对电机振动响应的影响，电机振动均值响应最大值的变异系数随输入变异系数和车速的变化规律，如图10所示。

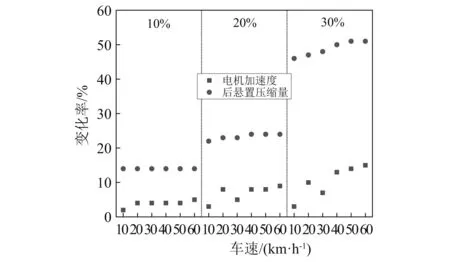
图10 电机振动响应最大值变异系数的变化规律Fig.10 Changing rules of variation coefficients for maximums of motor dynamics responses

由图10可知：总体来看，随输入变异系数的增大，各响应的变异系数不断增大，且随车速提高，各响应的变异系数总体呈现增大趋势；悬置压缩量响应的变异系数明显大于电机加速度，说明输入参数不确定对悬置压缩量影响更大。具体来看，在不同输入变异系数情况下，电机加速度和悬置压缩量最大值的变异系数可分别达到5%，9%，15%和14%，24%，51%，悬置压缩量最大值的变异系数甚至大于输入的变异系数。

基于各均值响应最大值的概率密度，其分布范围、均值和方差随输入变异系数和车速的变化规律，如图11所示。

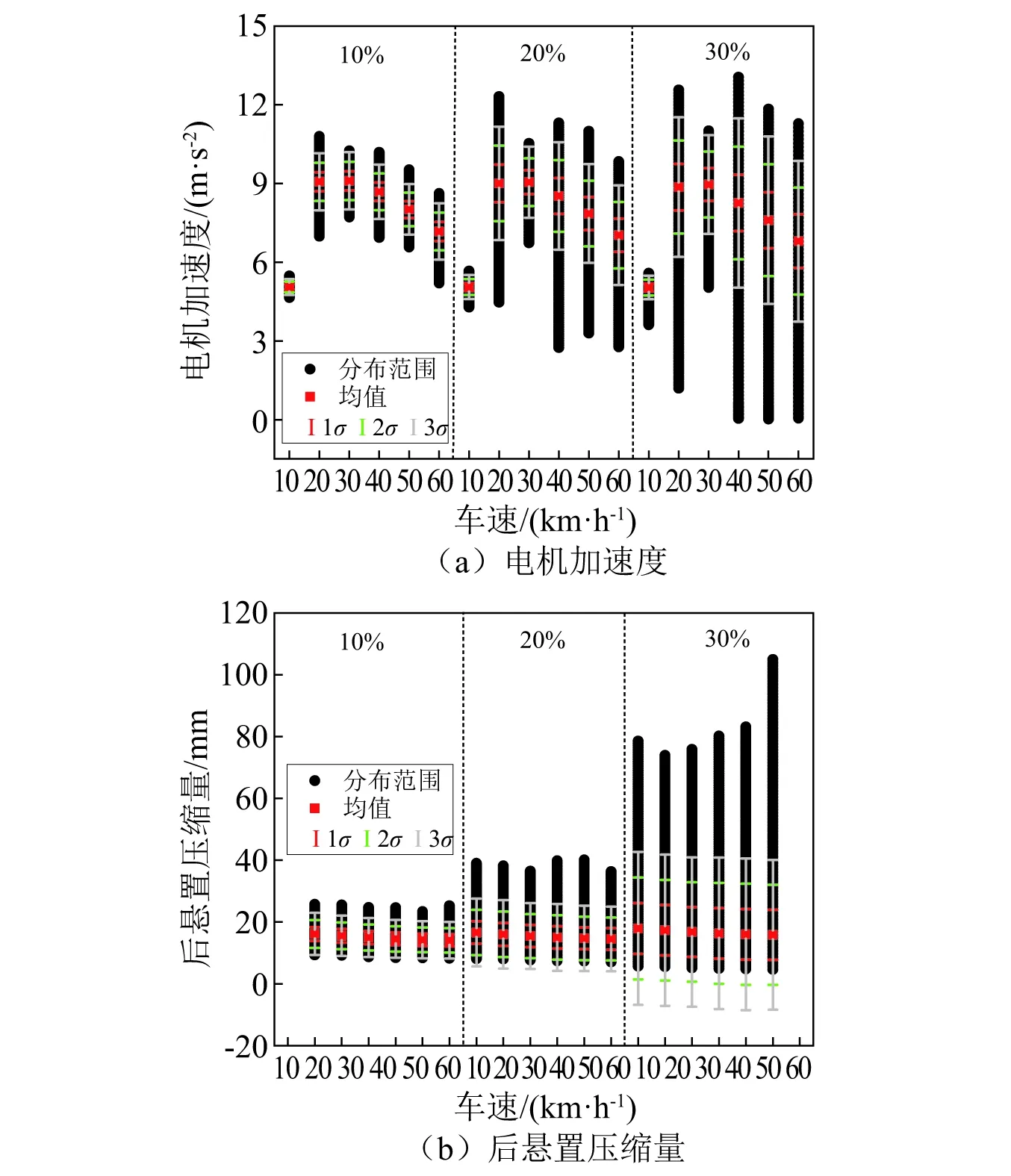
图11 电机振动响应最大值的均值、方差和分布范围变化规律Fig.11 Changing rules of means,variances and distribution ranges for maximums of motor dynamics responses

由图11可知：总体来看，随输入变异系数增大，各响应均值最大值变化不大，但其方差和分布范围增大，同样说明电机参数不确定主要影响响应方差和分布范围，对均值影响不大。随车速提高，电机加速度最大值均值总体下降，其方差和分布范围总体增大；悬置压缩量最大值均值、方差和分布范围随车速变化不明显。

根据电机各响应最大值的概率密度，图12给出其概率分布，并基于此计算了电机振动响应最大值超过设定阈值的概率。其中，电机加速度、悬置压缩量的阈值分别设置为0.9g和15 mm。

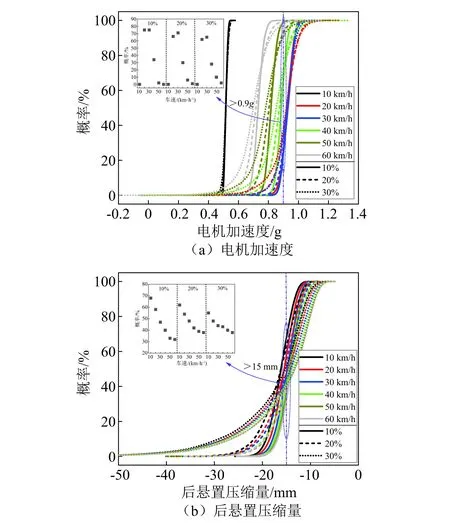
图12 电机振动响应最大值的概率分布及超限概率Fig.12 Probability distributions and overrun probabilities for maximums of motor dynamics responses

由图12可知：总体来看，随输入变异系数的降低，各响应概率分布曲线越来越陡峭，这与前述的响应最大值的分布范围变窄一致。从超限概率来看，不同输入变异系数下电机加速度超过0.9g的最大概率分别为75%，71%和65%，随输入变异系数增大超限概率最大值略有下降，除10 km/h车速外，超限概率总体随车速提高而降低，说明在小变异系数和低速时的电机加速度偏大；悬置压缩量超过设定值的最大概率分别为68%，62%和55%，随变异系数提高也略有降低，随车速提高超限概率也总体下降，说明在小变异系数和低速时悬置压缩量较大，其与电机加速度的规律类似。

3 结 论

本文基于广义多项式混沌理论和汽车动力学理论，建立了考虑电机参振的含不确定参数电动汽车的平顺性分析模型。以某型电动乘用车为例，计算分析了不同输入变异系数和车速条件下，车辆通过脉冲路面时两类参数不确定对各振动响应的影响程度和规律，得到如下结论：

(1)在电动汽车整车平顺性模型中，相比传统MC法，运用gPC理论能更快速有效度量参数不确定对各统计指标的影响程度。考虑参数的不确定后，对动力学响应的量值和规律分析更加全面，可为合理预测响应范围并对关键零部件的设计和可靠性评估提供建议。

(2)在所分析速度域内，随参数不确定程度的增加，各响应最大值的均值基本不变，但其方差、变异系数和分布范围均不断增大。当不确定参数变异系数为30%，车速为60 km/h时，各响应最大值的变异系数达到最大，部分响应的变异系数甚至超过输入变异系数。

(3)不同参数变异系数和车速条件下，超限概率的变化规律具有多样性，与所设置响应限值的大小及该响应随车速的变化规律有关。在小变异系数和低速时，车体加速度、轮胎载荷最小值、电机加速度和悬置压缩量超限概率偏大，在大变异系数和低速时悬架压缩量超限概率较大，而在大变异系数和高速时的轮胎载荷最大值超限概率较高。

附录A

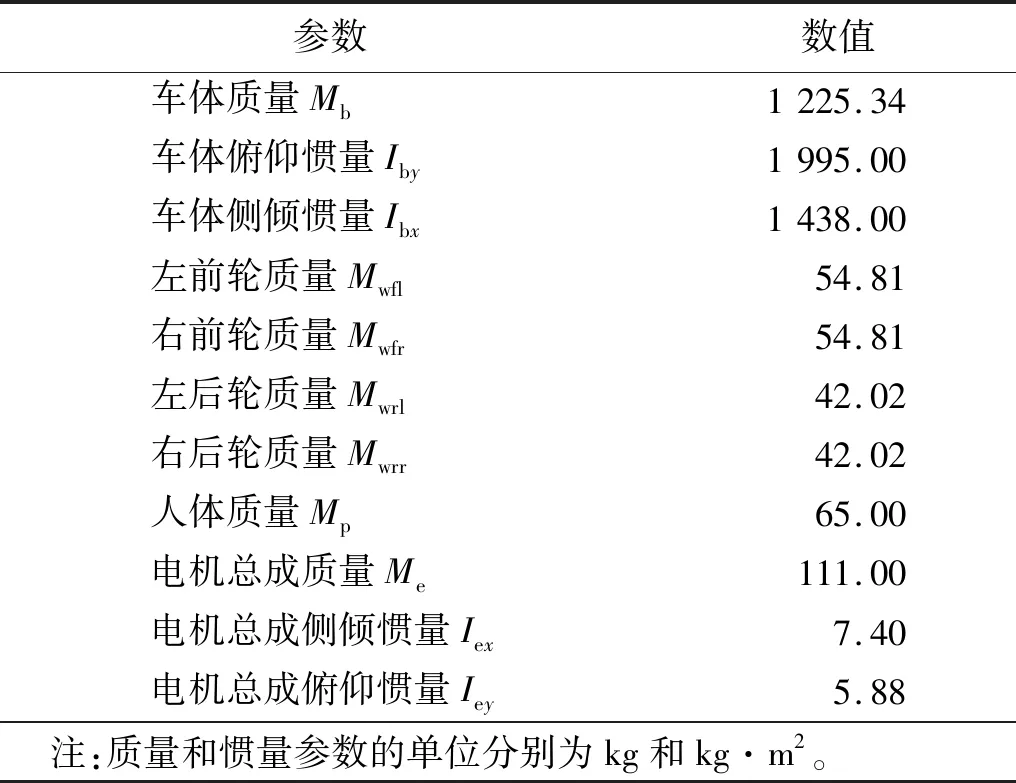
表A.1 考虑电机振动的电动汽车平顺性确定性模型质量及惯量参数Tab.A.1 Mass and inertia of the determined vertical dynamics model of electric vehicle considering electric motor vibration

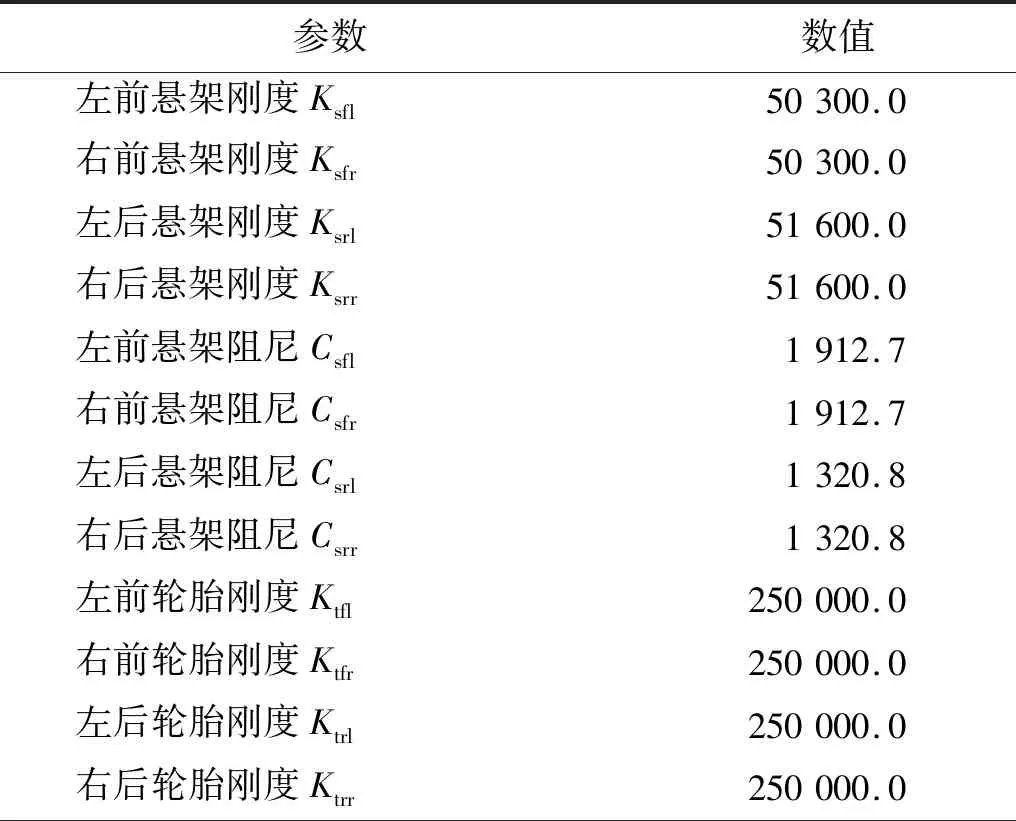
表A.2 考虑电机振动的电动汽车平顺性确定性模型刚度及阻尼参数Tab.A.2 Stiffness and damping of the determined vertical dynamics model of electric vehicle considering electric motor vibration

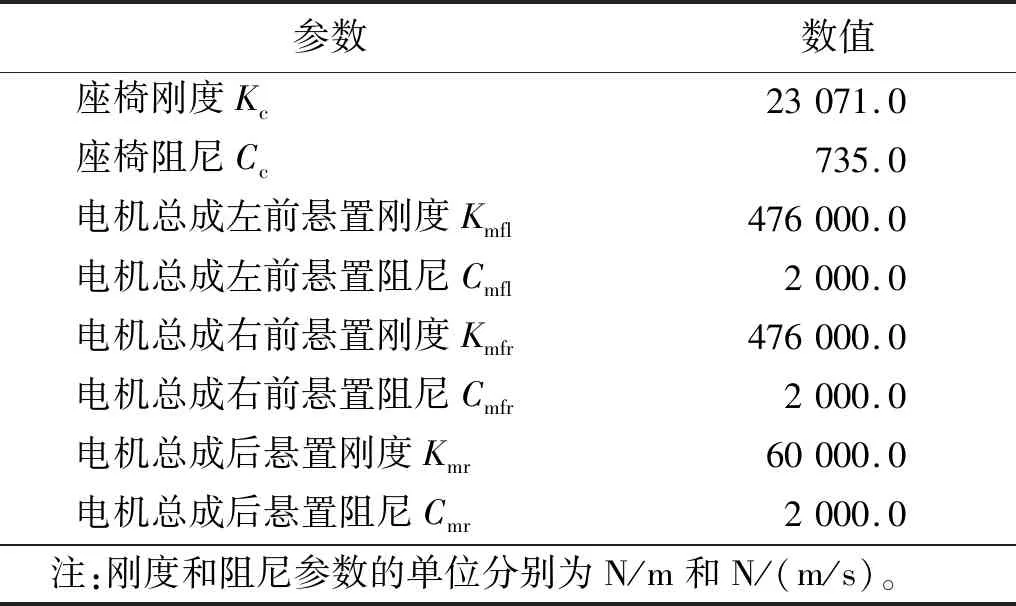
表A.2(续)

表A.3 考虑电机振动的电动汽车平顺性确定性模型几何尺寸及其他参数Tab.A.3 Geometric and other parameters of the determined vertical dynamics model of electric vehicle considering electric motor vibration