一种新型软粗糙模糊集及其在TOPSIS多属性决策中的应用
2021-09-27张方印
周 敏,张方印
(湖北民族大学 数学与统计学院,湖北恩施 445000)
§1 引言
为了更加有效地挖掘隐藏在不确定数据中的有用信息,数学,计算机科学及相关领域的研究人员建立了许多理论,如模糊集理论[1],粗糙集理论[2-4],软集理论[5-6]等.就其本质而言,模糊集理论强调隶属度,粗糙集理论强调粒度化,软集理论强调参数化.现实问题的解决往往非常复杂,因此,将这些理论结合起来是一条解决实际问题的有效途径.2007年,Aktas[7]等证实模糊集和粗糙集都可以看作软集,这不仅建立了这些理论之间的联系,也为将它们有效融合奠定了理论基础.事实上,为了更加高效地应用各种数学理论和方法解决实际问题,近年来,综合运用模糊集理论,粗糙集理论和软集理论建立混合模型来研究现实问题已成为一种趋势,与此相关的研究成果颇多.1990年,Dubois和Prade首先将模糊集和粗糙集结合,建立了模糊粗糙集和粗糙模糊集的概念[8].随后,Maji等在文[9]中将模糊集与软集结合引入了模糊软集的概念.在此基础上,冯锋等在文[10-12]中构建了一个将软集,模糊集和粗糙集高度结合的框架,引入了许多新的概念,如粗糙软集,软粗糙集和软粗糙模糊集.2011年,孟丹等发现冯锋提出的软粗糙模糊集与软粗糙集的联系不是很紧密,为了更好地研究软粗糙模糊集与软粗糙集之间的内在联系,他们又在文[13]中定义了一种新的软粗糙模糊集.受上述思想的启发,Sun和Ma在文[14]中将模糊软集和传统的模糊粗糙集结合,提出了软模糊粗糙集的概念.Ali等在文[15]中建立了软集,模糊软集和粗糙软集的之间的联系.Shabir在文[16]中定义了一种新的软粗糙集.Gong和Zhang基于模糊边界蕴含算子(I,J),建立了(I,J)-模糊软粗糙集模型,给出了上下近似的定义,并讨论了相关性质[17].从某种意义上来说,这些研究既整合了程度化,粒度化和参数化等重要思想,又指明了一个新的研究方向.尽管如此,还有一些基本问题仍然值得进一步研究.例如,文献[10]引入软粗糙模糊集从而建立了模糊集,粗糙集和软集的混合模型.但是,这些模型只对满软集有效,而在现实生活中,非满软集普遍存在,因此这一条件在实际应用中受到很大的局限(见例2.6).为了克服上述缺陷,本文通过引入一种新的软近似空间–MS-近似空间,建立了M-软粗糙模糊集的概念,并对其基本性质进行了深入讨论.
模糊拓扑是由Chang[18]提出的,是普通拓扑的推广,它不仅为模糊分类的发展提供了一种基本工具,而且为解决许多地理信息系统问题提供了一种重要工具.近几十年以来,学术界对模糊拓扑的研究非常活跃,并取得了许多重要的成果.同时,近年来,从拓扑学角度对粗糙集和软集的研究也受到了学者们的广泛关注,例如有关模糊粗糙集和模糊拓扑空间联系的研究[19].基于此,在提出了M-软粗糙模糊集的概念后,本文进一步建立了M-软粗糙模糊集与模糊拓扑之间的关系.最后,发现M-软粗糙可定义集生成了两个模糊拓扑空间,为模糊分类和空间信息管理提供了一种新的有效工具.
近年来,随着信息技术的迅猛发展,在不精确的环境中讨论决策问题已然成为一个热点(见文献[11,20,21,22,23]).TOPSIS(逼近于理想值的排序方法)是Hwang和Yoon[24]于1981年提出的一种适用于多个属性,能够对多个方案进行比较从而选择最优解的分析方法.后来,Qu[25]等应用粗糙集和信息增益的方法对初始指标体系进行约简,并利用TOPSIS方法对评价信息进行处理,有效地避免了信息失真和丢失,使评价结果更加精确.2006年,周珍,吴祈宗,彭艳丽[26]提出了一种基于VAGUE集多准则决策的模糊TOPSIS方法.随后,朱卫东等将相关系数矩阵与欧氏距离相结合,提出了一种新的TOPSIS决策方法[27].2017年,Yang和Peng[28]将模糊软集理论和TOPSIS方法相结合开展了富有现实意义的研究.最近,Suo等[29]将一种新的熵与TOPSIS方法相结合应用于犹豫模糊软集,得到了一种较好的决策方法.但截至目前,将TOPSIS方法与软粗糙模糊集相结合用于决策的研究并不多,鉴于此,为了充分发挥软集理论,粗糙集理论和模糊集理论在解决决策问题上的优势,本文在提出了一种新的信息表达方式—M-软粗糙模糊集之后,又建立了基于M-软粗糙模糊集的TOPSIS法的决策步骤和算法.最后,将其应用于购房问题中,发现该方法灵活有效.相关研究还能为医疗诊断,天气预测,人才选拔等提供一种新的方法.
§2 M-软粗糙模糊集
设U是初始论域,E是与U中的对象有关的所有参数的集合,称为参数空间.一般情况下,参数涉及对象的属性,特征或性质等.二元组(U,E)通常被称为软论域.论域中的所有子集构成的类称为U的幂集,记作P(U).
定义2.1[6]设A是参数集E的一个子集,F:A →P(U)是一个集值映射,二元组G=(F,A)是论域U上的一个软集,称F为软集G的近似函数.
定义2.2[1]设U是一个初始论域,隶属函数µ:U →[0,1]称为U上的一个模糊集.对U中的任意一个元素x,隶属值µ(x)表示x属于模糊集µ的程度.U上所有的模糊集记为F(U).特别地,设f ∈F(U),对U中的任意元x,如果f(x)≡1,则f记为f1;如果f(x)≡0,则记f为f0.
本文用到的模糊集的交,并和补运算具体定义如下:∀µ,ν ∈F(U),∀x ∈U,

另外,如果µ(x)≤ν(x),则记为µ⊆ν,如果µ⊆ν且ν ⊆µ,即µ(x)=ν(x),则记为µ=ν.
定义2.3[12]设U是一个初始论域,G=(F,A)是U上的一个软集.如果,则称软集G=(F,A)为U上的一个满软集.

注2.5上面的定义在现实问题的研究中有十分广泛的应用,但是,定义中“满软集”的条件比较苛刻,它在一定程度上限制了软粗糙模糊集的应用,例如下面一个例子.
例2.6假设有6套不同类型的房子供参考,即论域U={u1,u2,u3,u4,u5,u6},参数集A={e1,e2,e3,e4},其中,ei(i=1,2,3,4)分别表示“漂亮”,“便宜”,“房间设计好”,“楼层好”.现在X先生打算买房,用软集S=(F,A)表示对他有吸引力的房子.设软近似空间为P=(U,S).软集(F,A)还可以表示如下:

表2.1 软集(F,A)的图表表示
根据个人喜好,X先生的妻子也给出了她对这6套房子的建议,用下面一个模糊集来表示:

下面定义一种新的软粗糙模糊集,使其对非满软集也成立.
定义2.8设U是一个初始论域,(F,A)是U上的一个软集,定义从U到P(A)的集值映射

例2.9(续例2.6) 设论域U={u1,u2,u3,u4,u5,u6},参数集A={e1,e2,e3,e4},考虑例2.6中的软集(F,A),则(U,ϕ)是一个MS-近似空间,其中映射ϕ:U →P(A)的定义如下:

给定模糊集
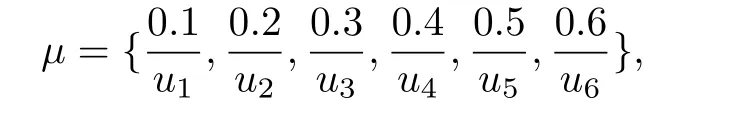
根据定义2.8,可得

注2.10在例2.9中,ϕ(u1)={e1,e4}表示房子u1具有两个属性,即漂亮和楼层好.类似地,可以描述论域U中其他房子的属性.因此,定义MS-近似空间既有实际背景,又提供了一种新的描述初始论域中元素的本质特征的新方法.另外,在例2.9中,.因此,可进一步定义模糊集µ的M-下软粗糙近似和M-上软粗糙近似.
定理2.11设U是一个初始论域,(F,A)是U上的一个软集,(U,ϕ)是一个MS-近似空间,则对U上的任意的模糊集µ,ν,有以下结论成立.

证(1) 由定义2.8知,结论显然成立.
(2) 由定义2.8和定义2.2知,结论成立.
(3) 证明类似于(2).

(5) 证明类似于(4).
(6) 设µ,ν是U上的任意两个模糊集,x是U中的任意一个元,且

(7) 设µ,ν是U上的任意两个模糊集,x是U中的任意一个元,且
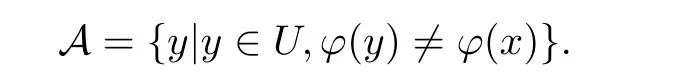
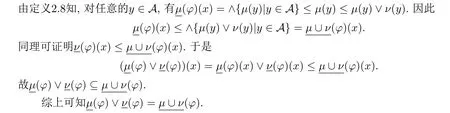
(8) 证明类似于(7).
(9) 证明类似于(8).
(10) 设µ,ν是U上的任意两个模糊集且满足µ⊆ν,x是U中的任意一个元,
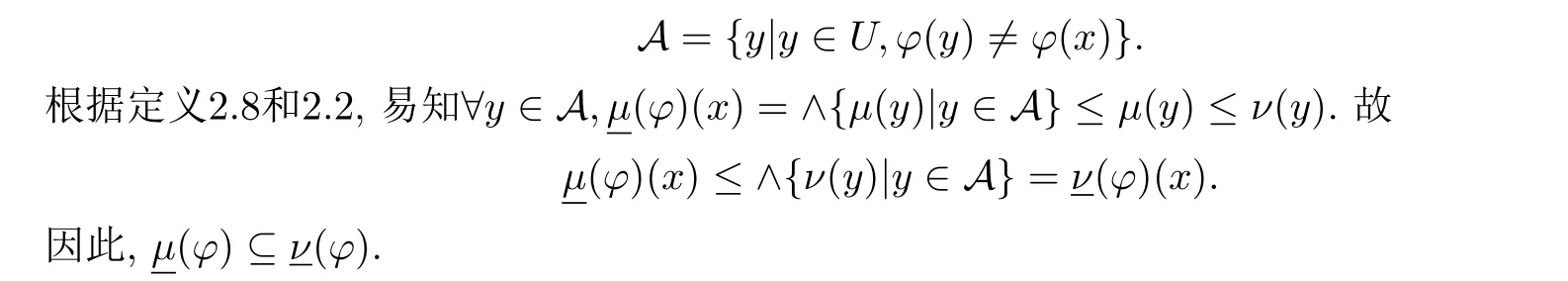
(11) 证明类似于(10).
例2.12设论域U={u1,u2,u3,u4,u5},参数集A={e1,e2,e3,e4},(F,A)是U上的一个软集,其图表表示如下.
由表2.2易知
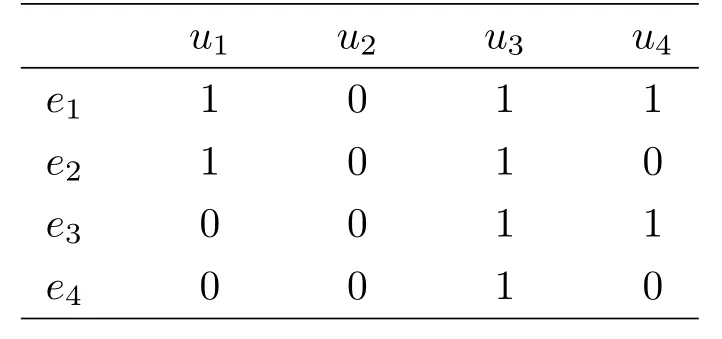
表2.2 软集(F,A)的图表表示
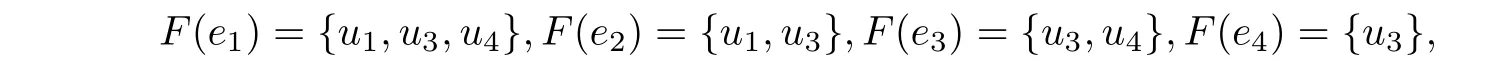
MS-近似空间(U,ϕ)的映射ϕ:U →P(A)为

另一方面,由定义2.2易知
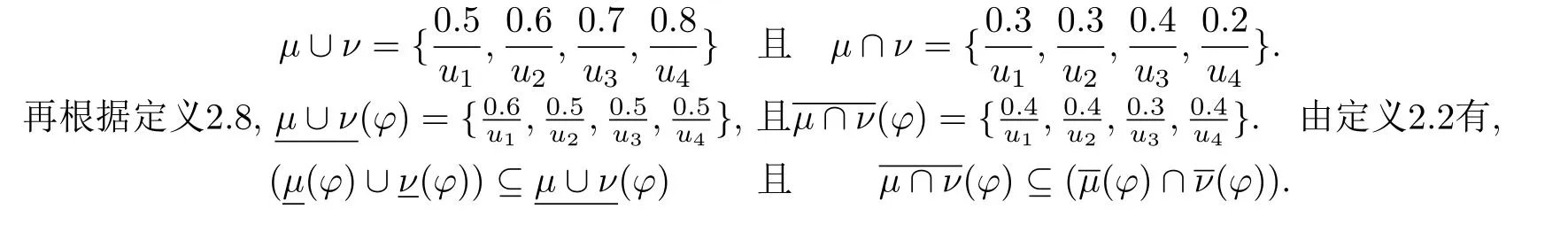
注2.13从上面的例子不难看出,定理2.11中的包含是真包含.
注2.14冯峰等在文[10]研究了软粗糙模糊集的上述性质,但是有一个较强的条件:软集(F,A)必须是满的.本文在定理2.11中,去掉了这个比较强的条件.另外,由定理2.11不难发现,M-软粗糙模糊集几乎具有由Pawlak提出的粗糙集的所有基本性质.然而,对M-软粗糙模糊集来说,也有一些遗憾,如在一般情况下,对U上的任意一个模糊集µ,.这里,(F,A)是U上的一个软集,(U,ϕ)是(F,A)上的一个MS-近似空间.
§3 M-软可定义集上的模糊拓扑结构
定理3.1设U是一个初始论域,(F,A)是U上的一个软集,(U,ϕ)是一个MS-近似空间,定义一个集族I如下:
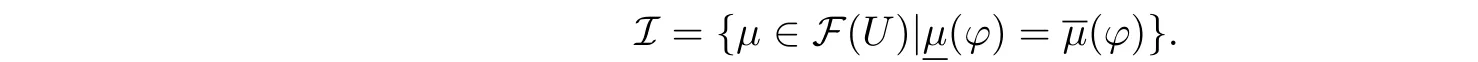
则I是U上的一个模糊拓扑,且模糊拓扑空间(U,I)中的每个开集都是闭集.


定理3.2设U是一个初始论域,(F,A)是U上的一个软集,(U,ϕ)是一个MS-近似空间,定义一个集族
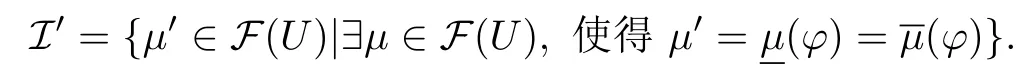
则I′是U上的一个模糊拓扑,且模糊拓扑空间(U,I′)中的每个开集都是闭集.
证类似于定理3.1.
§4 M-软粗糙模糊集在决策中的应用
随着社会、经济的飞速发展,决策过程中的不确定性因素越来越多,现有的许多数学模型已无法满足人们实际决策的需要.因此,许多学者开始融合多种数学模型来研究决策理论和方法.本文结合模糊集,粗糙集和软集理论提出一种新的信息表达方式—M-软粗糙模糊集,并把它与决策分析相结合.
4.1 基于M-软粗糙模糊集的一般决策方法
最近,Suo等[29]将相似熵度量与犹豫模糊软集相结合,得到了几种较好的决策方法.受此启发,为了探究软粗糙模糊集在决策中的应用,本节提出一个基于M-软粗糙模糊集模型的一般决策算法.
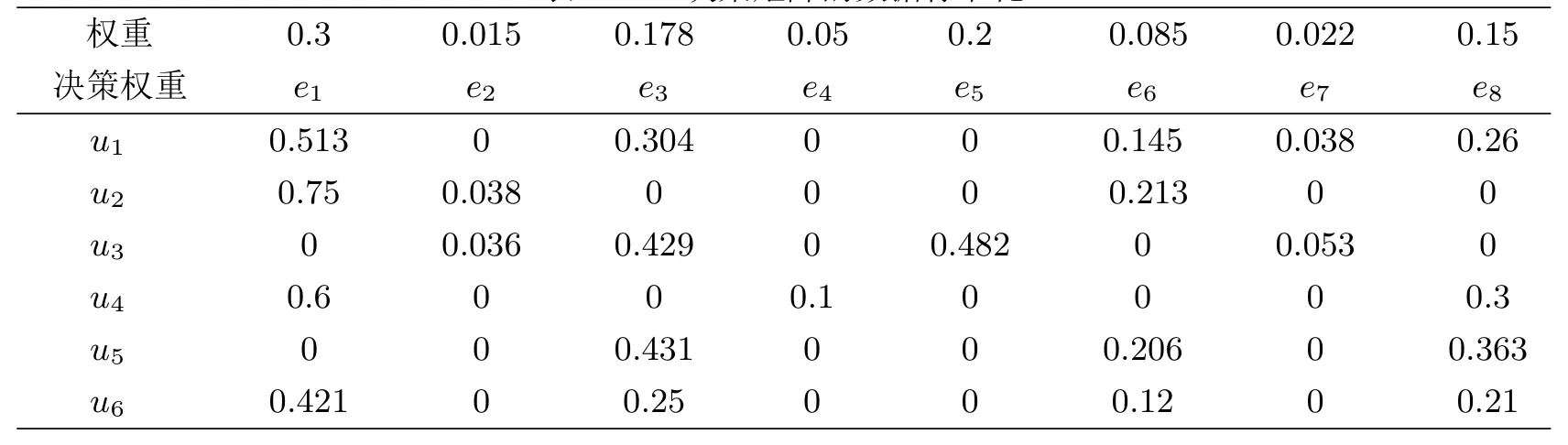
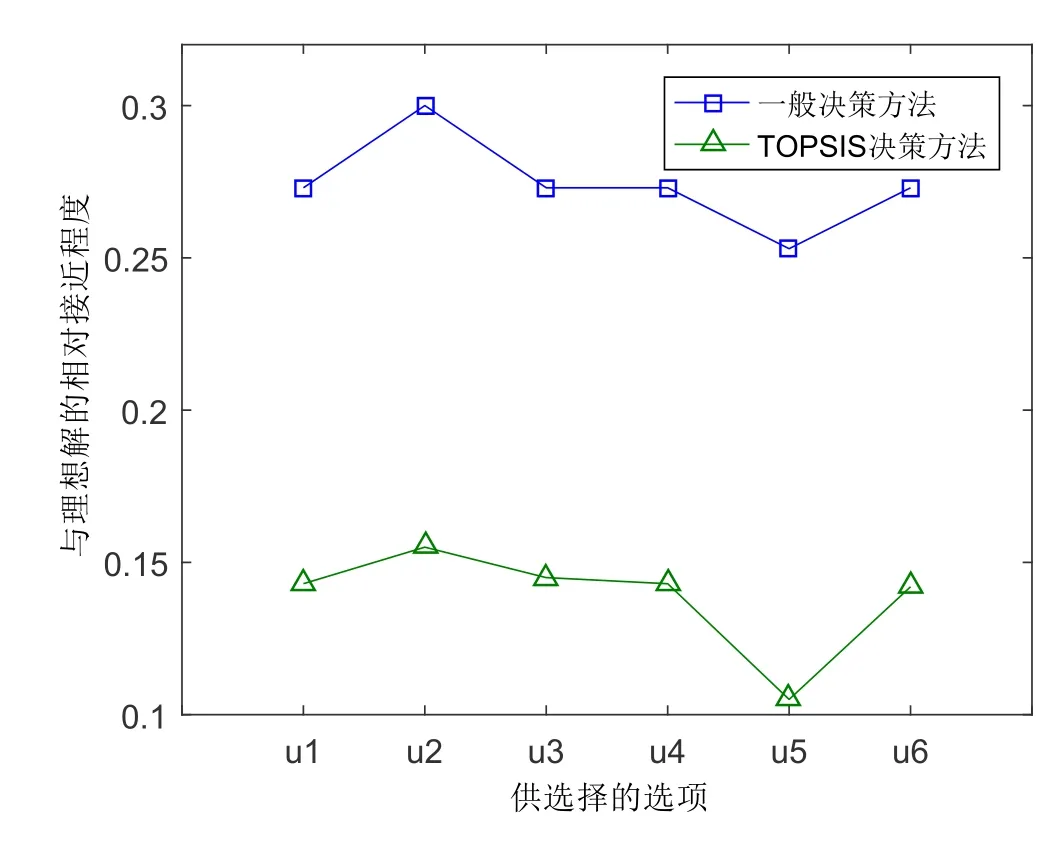
设U={u1,u2,……,ul}是一个初始论域,E={e1,e2,……,en}是一个参数集,集合A={e1,e2,……,em}(m 这里,ui ∈U. 步骤4:如果Ck=max{Ci:i=1,2,……,|U|},则决策就是uk ∈U,这里,|U|表示U中元素的个数. 步骤5:如果k有一个以上的值,则任何一个uk可以选择. 步骤6:输出uk. 例4.1.1假设(F,A)是集合U={u1,u2,u3,u4,u5,u6}上的软集,其中U是供选择的房子.A={e1,e2,e3,e4,e5,e6,e7,e8}是一组参数,其中ei(i=1,2,3,4,5,6,7,8)分别代表“小区环境”,“便宜”,“设计良好”,“公摊面积”,“交通便利”,“医疗配置齐全”,“有无学校”和“贷款年限长”.X先生考虑购买的房子用软集合(F,A)表示如下: 表4.1 软集(F,A)的图表表示 根据如上决策方法,可得下列结果. 由步骤5知X先生选择的最佳房源为u2,最先排除的房源为u5. 注4.1.2在例4.1.1中,虽然选出了最佳房源,排除了最差房源,但房源u1,u3,u4,u6的优先等级完全相同,一旦决策者不选择房源u2,后面的决断难度就加大了.为了将决策结果有效排序,进一步探讨下面的决策算法. 逼近理想解排序(TOPSIS)法是最常用的多属性群决策方法.常规的TOPSIS方法是用精确数,模糊数,区间数,直觉模糊数,区间直觉模糊数以及犹豫模糊元来表示决策信息的.但是,对于多属性群决策中以粗糙模糊元表示决策信息的情形,常规的TOPSIS方法不能有效地解决.为此,本文将TOPSIS法和M-软粗糙模糊集相结合提出了基于M-软粗糙模糊集的TOPSIS法,用于解决属性评价值为粗糙模糊元的多属性群决策问题,并将本文的算法应用到实例中选出最佳备选方案.下面,给出基于M-软粗糙模糊集的TOPSIS方法在决策中的具体算法: 步骤1:假设有m个备选方案,每个备选方案有n个决策标准,其属性值用 表示决策者需要根据决策标准在众多备选方案中选择一个最优选项,这里的最优指综合意义上的最优. 步骤2:构造决策矩阵如下: 表4.2.1 决策矩阵 步骤3:把决策矩阵中的数据标准化处理 步骤4:根据如下公式计算正理想解A+与负理想解A−: 其中µej(xi)是对象关于属性评估值的隶属度(由于隶属度为0的选项不具有考虑价值,故计算时舍去隶属度为0的值). 步骤5:根据定义2.8分别计算A+及A−的上下近似算子如下: 步骤6:定义 其中α,1−α分别表示对A+及A−的上下近似算子的权重(由决策者给出),α的范围是0≤α≤1. 步骤7:根据下列公式计算各备选方案与理想解的相对接近度并对各备选方案进行排序 Ri=1越接近于1,表明该选项距离正理想解越近,从而该选项越优. 例4.2.1在与例4.1.1相同的条件下(其中的权重由专家给定),用基于M-软粗糙模糊集的TOPSIS决策方法计算,得到下列结果: 步骤1:根据公式(4.2a)对表4.1 软集(F,A)中的数据进行标准化处理,结果如表4.2.1所示. 表4.2.1 决策矩阵的数据标准化 步骤2:根据公式(4.2b)和(4.2c),分别得正理想解 和负理想解 步骤3:根据公式(2.1a)和(2.1b)分别计算A+及A−的上下近似算子如下. 步骤4:由α=0.3,根据公式(5.2d)和(5.2e)易得 步骤5:根据公式(5.2f)计算各备选方案与理想解的相对接近度,可得 从而决策结果可排序如下:u2>u3>u1=u4>u6>u5.因而优先考虑u2. 为了更好地比较前面两种决策方法的优劣,给出它们的排序结果的直观图,如图1所示. 注4.2.2根据图1,两种方法的最优选项和最差选项相同且所得结果高度一致,这说明两种决策方法都可行.但从中间房源的优先层次来看,一般决策方法中处于同一等级的较多,区分度不高,而TOPSIS方法中处于同一等级的较少,因而决策信息更灵敏.故基于M-软粗糙模糊集的TOPSIS决策方法较一般决策方法更具有优越性. 图1 两种决策方法的比较 注4.2.3在[11]中,冯峰等人讨论了Roy-Maji方法的有效性,详细说明了其真正的局限性,并借助于水平软集提出了一种新的基于模糊软集的决策方法.尽管[11]中的方法克服了[22]中的缺点,但决策者需要提前选择阈值.因此,结果在一定程度上取决于阈值.在本文中,基于M-软粗糙模糊集的TOPSIS决策方法的结果也在一定程度上依赖于阈值.在例4.2.1中考虑了不确定因素对A+及A−的上下近似算子的权重(其他因素是在本文中定义为确定的),接下来为提高算法的适用范围,对不确定因素进行敏感性分析,并根据分析结果,提出相应措施. 例4.2.4在与例4.1.1相同的条件下,得到的A+及A−的上下近似算子的结果与例4.2.1相同.当水平调节值α为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9时,则通过计算得到排序结果的直观图,如图2所示. 图2 不同α值下基于M-软粗糙模糊集的TOPSIS决策方法的排序结果 由图2可知,决策者给定的A+及A−的上下近似算子的权重对最优选项的结果有重要影响,权重α是敏感元素.为了避免敏感元素对决策结果的影响,进行如下探讨. 下面,根据已知的基于M-软粗糙模糊集的TOPSIS方法,给出基于M-软粗糙模糊集的改进TOPSIS方法的具体算法:步骤1,步骤2,步骤3,步骤4,步骤5和步骤7均不变,与基于M-软粗糙模糊集的TOPSIS方法的步骤1,步骤2,步骤3,步骤4,步骤5和步骤7相同.步骤6改为:在实际决策中决策者更加注重正理想解,而不是负理想解的结果.故改进的决策方法只对正理想解乘上权重.根据公式 这里α,1−α分别表示对A+及A−的上,下近似算子的权重(由决策者给出),且0≤α ≤1. 例4.3.1在与例4.2.5相同的条件下,根据上述算法,当α取不同值时,计算结果如图3所示. 图3 不同α值下基于M-软粗糙模糊集的改进TOPSIS决策方法的排序结果 注4.3.2观察图3可知,直接得到排序结果的变化不大.与图2的排序结果比较知,改进后的决策算法能消除敏感因素对排序结果的影响,避免出现极端条件对整体决策的影响. 注4.3.3由图3不难发现,无论α取何值,由改进后的方法得到的排序结果都基本相同,且最优选择都是一样的.而从图2知,TOPSIS方法得到的排序结果会随着α取值的变化而改变.基于M-软粗糙模糊集的TOPSIS决策方法和基于M-软粗糙模糊集改进后的TOPSIS决策方法均需要决策者提供的可用信息,这难免导致主观信息对决策结果的影响.但是,在不同专家主观因素的影响下,通过改进后的方法得到的排序结果基本相同,从而结果更加客观. 软粗糙模糊集是一种将模糊集,粗糙集和软集理论有效融合起来处理不确定性问题的有效工具.为了扩大冯峰等在文献[10]中定义的软粗糙模糊集的应用范围,本文通过构造MS-近似空间,提出了一种新的软粗糙模糊集――M-软粗糙模糊集,从而把软粗糙模糊集推广到了非满软集上,并研究了它的一些基本性质.在理论上,首先给出了由M-软粗糙可定义集生成的两个模糊拓扑空间,为模糊分类和空间信息管理提供了一种新的理论工具.在应用上,基于M-软粗糙模糊集,本文提出了一般决策方法,TOPSIS决策方法及改进的TOPSIS决策方法.最后通过实例比较发现,改进的TOPSIS决策方法最优.虽然提出的M-软粗糙模糊集比冯峰等提出的软粗糙模糊集适合更广泛的范围,但是,M-软粗糙模糊集的定义仍然不完美:首先,在Pawlak 粗糙集中,对任意一个模糊集,它的上近似包含它自身,且它自身包含它的下近似.然而在M-软粗糙模糊集中,对任意一个模糊集. 其次,当软集是满软集时,并没有找到M-软粗糙模糊集与冯峰定义的软粗糙模糊集之间的内在联系.在未来的研究中,将着力解决这些问题.
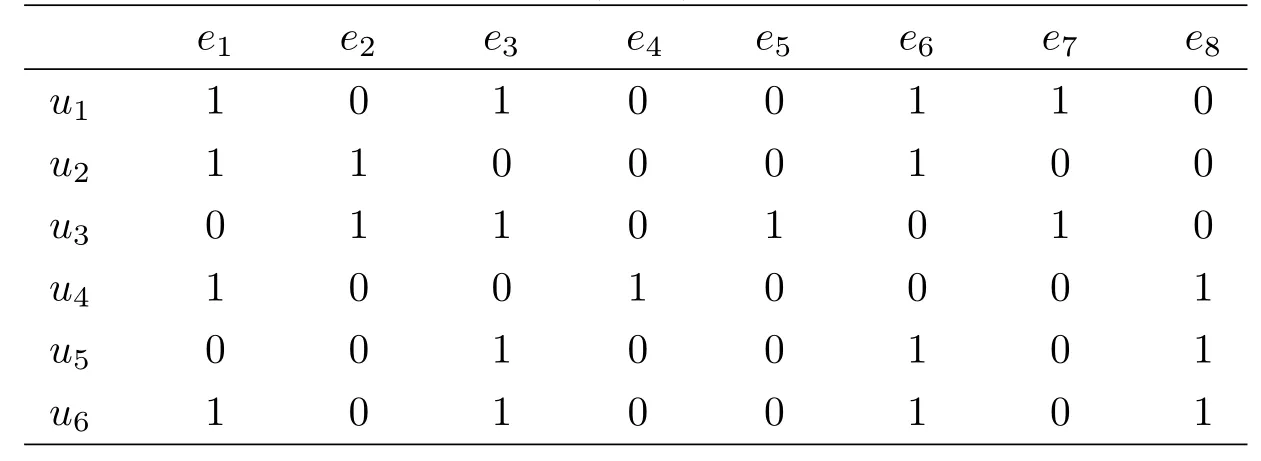

4.2 基于M-软粗糙模糊集的TOPSIS决策方法




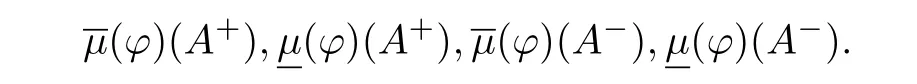

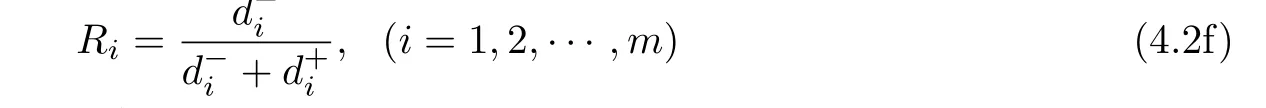



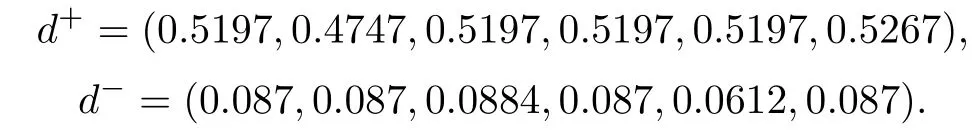


4.3 基于M-软粗糙模糊集的改进TOPSIS方法


§5 结论
