Riemann流形上的一类标准共形不变度量

施 云

(浙江科技学院理学院,浙江杭州 310023)

§1 引言

Araklov在紧Riemann面上利用Bergman度量的Green函数构造了一个共形不变度量[1].Leutwiler在Rn的局部邻域上构造了一个类似的共形不变度量[2].Harbermann和Jost在数量曲率为正的局部共形平坦流形上构造了一个标准共形不变度量[3-4].在此之后,王伟构造了CR流形上的Yamabe算子,数量曲率为正的球型CR流形上Green函数,并用此Green函数构造了上述共形不变度量[5].在[6]中,作者研究了四元切触版本的上述问题,构造了四元切触流形上的Yamabe算子,数量曲率为正的球型四元切触流形上Green函数,并用此Green函数构造了一个共形不变张量,证明了该共形不变张量在四元切触正质量猜测成立的情况下是一个共形不变度量.最近此研究推广到了八元切触流形上[7].在[8]中还给出了Heisenberg群上邻域版本的上述共形不变切触形式,并由此切触形式构造了一个邻域上的拟双曲Carnot-Carath´eodory不变度量.

本文利用Paneitz算子对应的Green函数在局部共形平坦流形上构造了上述共形不变度量.

§2介绍了Riemann几何的一些基本概念,给出了Riemann流形上的Paneitz算子以及Q曲率的定义并介绍了[9-10]中给出的Riemann流形上Paneitz算子对应的正质量定理. §3证明了本文的主要定理,即应用Paneitz算子对应的Green函数以及该Green函数在共形变换下的变换公式,构造出一类新的共形不变度量.最后,给出了该共形不变度量的一些性质.

§2 预备知识

Q曲率首先在[11]中引入,Chang,Gursky,Yang对4维流形上的Paneitz算子和Q曲率进行了深入的研究[12].在此之后,高维流形上的Paneitz算子和Q曲率问题受到越来越多的数学家的关注,成为当今共形微分几何与几何分析研究的一个重要的课题.更多关于Q曲率与Paneitz算子相关的研究参见[13-16]及其参考文献.最近,Q曲率问题还被推广到了CR流形和四元切触流形上[17-20].

记(M,g)为n维光滑的紧Riemann流形,φ ∈C∞(M)是M上的函数,于是

称为Riemann度量g的共形变换.形为e2φg的度量的全体所构成的集合称为g的共形类,记为[g].

对于度量g,

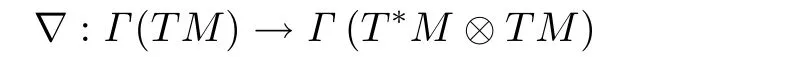
表示相应的Levi-Civita联络,这定义了向量空间Γ(TM)=X(M)上的一个满足

的协变导数

令R表示Riemann流形(M,g)上的曲率张量,那么对于任意的X,Y ∈TM,有

Ricci曲率张量定义为

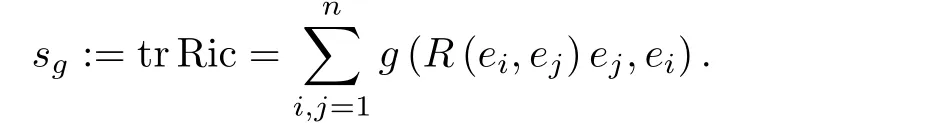
当f ∈C∞(M),对于任意X ∈TM,梯度gradg(f)∈X(M)定义为

对X,Y ∈TM,f的Hessian形式定义为

Ricci曲率在共形变换(1)下的变换公式为(参见[16,21])

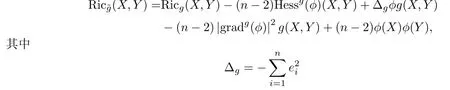
是M上的Laplacian算子.

进一步的,可以给出数量曲率在共形变换(1)下的变换公式(参见[16,21])

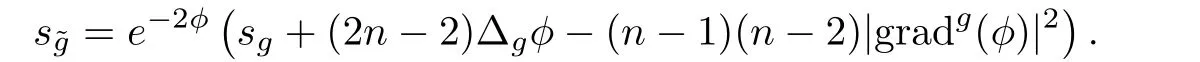
当n ≥3时,Schouten张量定义为

因此有(参见[16,21])

当n ≥3,Riemann流形上的Q曲率Qg定义为

通过简单的计算,有

Paneitz算子Pg的定义为

其中∇gφ=(e1φ,……,enφ).这是一个共形协变算子.为了方便计算,下文中通过适当的变换把共形变换(1)写成

在该共形变换下,Paneitz算子满足如下变换公式(参见[10,16])

其中f为任意光滑实函数.一个连续的函数

称为Paneitz算子Pg的Green函数,如果对于任意的u,满足

其中δx是在x处的Dirac函数.在共形变换(3)下,有如下Riemann流形上的体积元的变换公式(参见[10])

Green函数在共形变换(3)下的变换公式如下.

证由体积元在共形变换下的变换公式(5)以及Paneitz算子在共形变换下的变换公式(4),

由Green函数的唯一性,命题得证.

紧Riemann流形(M,g)(dimM ≥3)的Yamabe算子定义为(参见[21])

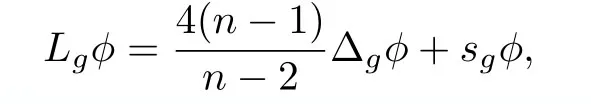
其中φ是(M,g)上的任意光滑函数.Yamabe不变量定义为

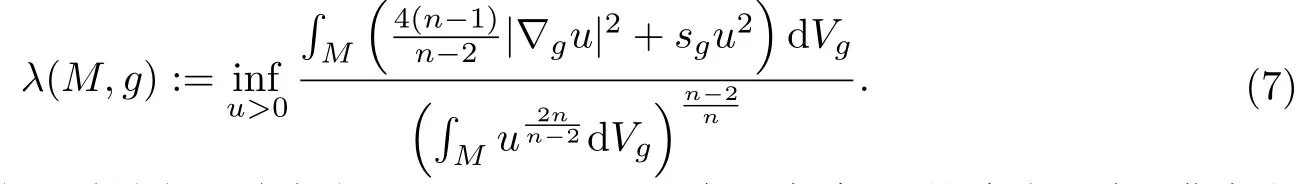
Paneitz算子对应的正质量定理首先由Humbert和Raulot在[9]中给出.这个定理在Q曲率方程中的作用与传统的正质量定理在Yamabe问题中的作用类似.在[10]中,作者用其他方法证明了类似的定理.当n>4时,有如下Paneitz算子的正质量定理.

定理2.1(参见[9,定理1.1])假设g是共形平坦的,n >4,λ(M,g)>0,Paneitz算子是正的,

上式取等号当且仅当(M,g)共形微分同胚于单位球面Sn.

§3 共形变换下的不变度量

令d(·,·)表示度量g下的距离,定义

定义n维Riemann流形(M,g)上的一类标准共形不变度量如下

下面给出本文的主要结论.

定理3.1can(g)是一个C∞共形不变张量,即在共形变换(3)下,

进一步的,当g是共形平坦的,n>4,λ(M,g)>0,Pg是正的,在M{y}上GP,g >0且(M,g)不共形微分同胚于单位球面Sn时,can(g)是一个C∞共形不变度量.

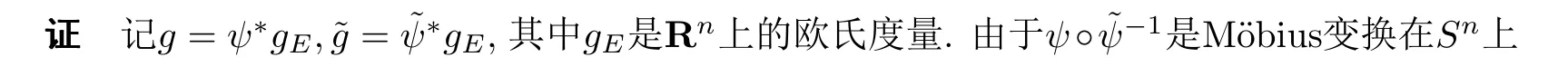
(参见[3,22]).因此,由Green函数在共形变换下的变换公式(6)以及(11),有

当g是共形平坦的,n>4,λ(M,g)>0,Pg是正的且在M{y}上GP,g >0时,由Paneitz算子的正质量(定理2.1)有

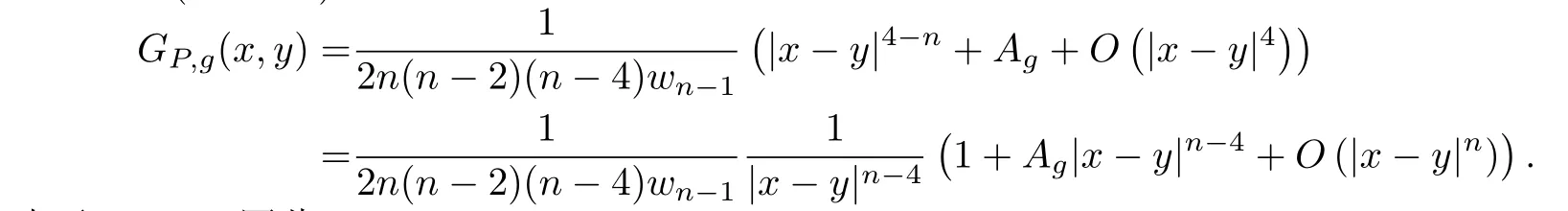
由于Ag >0,因此

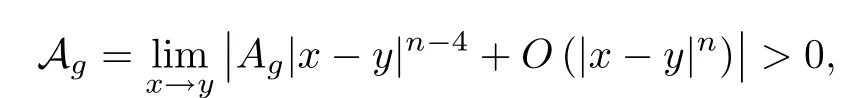
故can(g)进一步的是一个C∞共形不变度量.

下面给出该共形不变度量的一些性质.

命题3.1(M1,g1),(M2,g2)为两个连通的,紧的,满足dimM1=dimM2>4,以及正质量定理(定理2.1)的条件的Riemann流形,并且他们均不局部同胚于标准球面Sn.f:(M1,g1)→(M2,g2)为局部微分同胚,那么对于任意的X,Y ∈TM,有

其中Γ是一个覆盖群且y ∈M1,f(x)/=f(y).

在上面第三个等式中,应用了

以及GP,g1(x,γy)>0两个事实.因此,对于任意的X,Y ∈TM,有

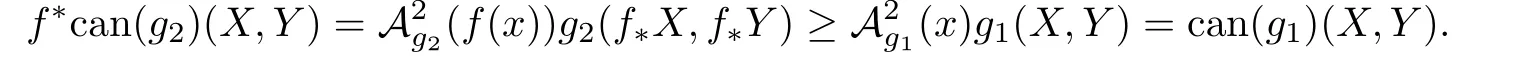
进一步的,有如下推论.

推论3.1(M1,g1),(M2,g2)为两个连通的,紧的,满足dimM1=dimM2>4以及正质量(定理2.1)的条件的Riemann流形,并且他们均不局部同胚于标准球面Sn.如果f是一个微分同胚,那么f∗can(g2)=can(g1).