MHD角速度传感器在冲击碰撞中的应用研究
2021-09-27黄子安李醒飞
黄子安,李醒飞
(天津大学精密仪器与光电子工程学院,天津 300072)
0 引言
在汽车碰撞试验中,由于假人自身惯性、安全带束缚及座椅的支撑作用,头颈部会前倾后仰产生角速度,该角速度的测量对于研究头部扭转伤害[1]以及头部运动轨迹具有重要意义。在国外早期碰撞试验中,角速度测量通常采用线加速度传感器阵列、高速相机和旋转电位计[2]。线加速度传感器阵列的测量精度易受到传感器间的失配、敏感轴不重合以及积分累积误差的影响。高速相机的视野易被假人挥动的四肢及车身结构遮挡,具有较大的局限性。旋转电位计的抗冲击性能较差,其安装位置有着严格要求。
MHD角速度传感器是抗冲击、宽频带、大量程传感器,由美国ATA公司1989年开发研制[3],并成功应用到汽车碰撞试验中,能准确可靠地测量假人头部和躯干的旋转。国内MHD角速度传感器研制起步较晚,目前处于原理样机阶段,已能有效敏感角速度,具有宽频带和大量程特性,但还未开展汽车碰撞相关应用研究。为了测试MHD角速度传感器是否能在高冲击环境下保持原有的测量性能,本文参考国外座椅鞭打试验数据[4](假人头部加速度峰值和3 ms合成加速度不超过28g,合成角加速度峰值不超过1 374 rad/s2),设计了摆锤式冲击试验装置,可产生类似半正弦的冲击波形。基于橡胶Mooney-Rivlin本构关系建立碰撞动力学理论模型,并根据电磁感应原理建立MHD角速度传感器输出模型。通过采用Hypermesh/LS-DYNA和Fluent仿真软件,对所设计装置的结构动力学响应及MHD角速度传感器输出电势进行仿真,并将仿真结果与计算结果进行对比分析,为后续研究提供理论基础。
1 冲击试验方案及理论模型建立
1.1 冲击试验方案
汽车碰撞试验主要考量假人头、胸、腿等部位受冲击的程度。本文基于MHD角速度传感器测试假人头颈部受冲击后加速度和角加速度的变化情况,利用摆锤结构产生冲击角速度,试验装置示意图如图1所示。摆锤自由释放后绕转轴运动到最低点时,以一定初速度与橡胶波形发生器发生碰撞,利用橡胶变形能的储存和释放产生类似半正弦的冲击加速度波形,该冲击通过摆锤机械传递给传感器工装上的MHD角速度传感器和线加速度计。
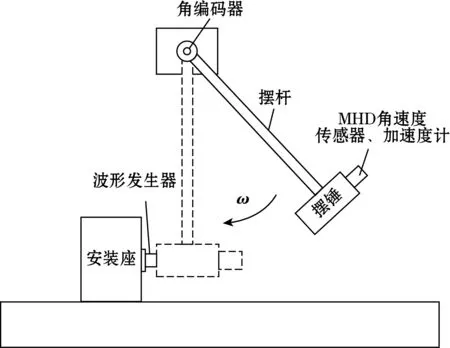
图1 摆锤式冲击试验装置示意图
MHD角速度传感器用于测量摆锤绕轴转动的角速度,线加速度计测量碰撞过程中摆锤的切向加速度。角编码器安装于转轴处,测量摆锤绕轴旋转的角位移,作为角位移的测量基准。
1.2 动力学理论模型建立
初始冲击速度是指摆锤与波形发生器发生碰撞瞬间的初始速度。若忽略机械摩擦及各种阻力,由机械能守恒定律,有
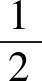
(1)
式中:M为摆锤和传感器工装总质量;v0为摆锤初始冲击速度;l为摆锤质心到转轴的距离;α为摆锤的摆角。
由式(1)可得,初始冲击速度为
(2)
初始角速度为
(3)
摆锤与波形发生器均为圆柱体,两者发生碰撞时的示意图如图2所示。规定碰撞瞬间为零时刻点,波形发生器的自由表面中心为坐标原点,水平向右为x轴正方向。由于在碰撞期间摆锤摆角很小,可近似地认为橡胶弹性恢复力始终沿水平方向。根据牛顿第一定律,其运动方程为
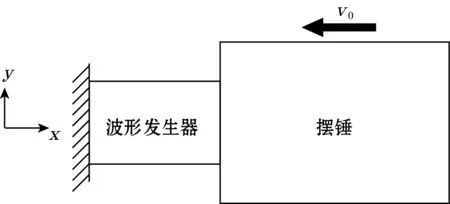
图2 碰撞示意图
Mü+F(u)=0
(4)
式中:F(u)为橡胶波形发生器的恢复力,是摆锤沿x轴方向位移u的函数;ü为摆锤沿x轴方向加速度。
一般使用橡胶作为半正弦波形发生器。橡胶是超弹性材料,常用应变能密度函数来描述其本构模型。其中Mooney-Rivlin模型在小应变时具有较高的准确性[5]。
两参数Mooney-Rivlin本构函数可表示为
W=C10(I1-3)+C01(I2-3)
(5)
式中:W为应变能密度;C10和C01为Mooney-Rivlin系数;I1、I2为第一、第二Green应变不变量。
根据文献[6]的推导,橡胶在单轴压缩应力应变关系可表示为
(6)
式中:ε为名义应变;σ为名义应力。
通常情况下,橡胶材料参数由压缩、拉伸、剪切等试验数据拟合而得,但这种方法花费时间较长,成本较高,应用起来不方便。由于橡胶材料硬度测量较为容易,本文根据橡胶IRHD硬度Hr与初始弹性模量E0试验数据拟合曲线[7]:
log10E0=0.019 8Hr-0.543 2
(7)
以及经验公式:
(8)
C01=0.25C10
(9)
即可在已知橡胶材料硬度的情况下,直接计算出橡胶材料参数的经验值。
由式(6)可推导出橡胶恢复力与位移间的关系:
(10)
式中:S0为波形发生器初始截面积;h0为波形发生器初始长度。
在碰撞过程中,有:
u≈lθ
(11)
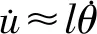
(12)
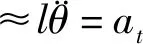
(13)

联立式(4)和式(10),并引入初始条件,可得二阶常微分方程:
(14)
1.3 MHD角速度传感器理论模型建立
MHD角速度传感器是利用电磁感应原理敏感角速度的,其工作原理示意图如图3所示。传感器与待测载体相固定,当载体以角速度ω旋转时,传感器中的导电流体因惯性与磁场存在相对运动从而切割磁感应线,在导电流体内外壁电极上产生感应电势。根据电磁感应定律可以得到其传递函数[8]:

图3 MHD角速度传感器工作原理示意图
(15)
式中:B为磁场强度;L为流体环宽度;r为流体环等效半径;h为流体通道高度;υ为运动黏度;H为哈特曼常数。
传递函数呈高通特性,具有较大的带宽,在通频段内传感器输出电势与载体角速度之比为常数,即E/ω=BLr。传感器工作在开环状态,能敏感较大的角速度。由于导电流体与传感器壳体不存在机械摩擦,因此MHD角速度传感器的抗冲击性能很好。
本课题组研制的MHD角速度传感器在降噪处理后带宽能达到1 kHz,测量角速度范围大于9 rad/s,满足本文试验装置带宽与量程需求。
2 数值计算及仿真
2.1 冲击波形的数值计算及仿真
2.1.1 试验装置结构参数设计
试验装置设计的主要原则有:
(1)可产生类似于半正弦的加速度波形,在可调范围内,最大加速度峰值和3 ms合成加速度超过28g,角加速度峰值超过1 374 rad/s2;
(2)合理选择摆锤参数,避免在碰撞时产生共振;
(3)保证结构具有一定的刚度,避免部件变形对冲击波形产生影响。
通过对冲击试验装置的初步设计,试验装置的主要参数有:摆锤质心到转轴的距离l=500 mm,最大摆角αmax=150°,摆锤和传感器工装总质量M=1.7 kg,波形发生器初始截面积S0=400π mm2,波形发生器初始长度u0=60 mm,橡胶硬度Hr=80 IRHD,对应参数C10=1.46 MPa,C01=0.365 MPa。
2.1.2 冲击波形的数值计算
根据碰撞动力学模型式(12),代入初始条件后可利用Runge-Kutta法进行数值计算得到摆锤在碰撞过程中的冲击响应。根据摆锤在不同摆角下获得的初始冲击速度,分别取为0.5、1、2、3 m/s进行计算,以探究摆锤的初速度对冲击波形的影响。计算得到摆锤冲击加速度-时间曲线如图4所示。
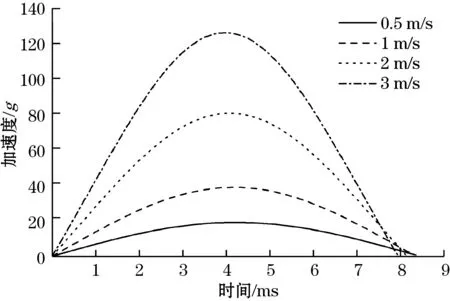
图4 不同初速度下摆锤加速度-时间曲线(计算)
为了探究橡胶硬度对冲击波形的影响,C10和C01分别取不同橡胶硬度Hr对应的经验值(见表1),摆锤初速度取-1 m/s,其余参数保持不变进行求解。得到在不同橡胶硬度下摆锤冲击加速度-时间曲线如图5所示。

表1 不同橡胶硬度对应的参数经验值

图5 不同橡胶硬度下摆锤加速度-时间曲线(计算)
2.1.3 摆锤结构动力学特性仿真
由于碰撞动力学模型简化了诸多条件,为了更好地了解摆锤与波形发生器的碰撞过程以及MHD角速度传感器的冲击响应,并验证已有理论模型的正确性,进行有限元仿真分析。
根据试验装置初步设计的主要参数,利用Solidworks绘制试验装置的简化三维模型,如图6所示。将三维模型导入Hypermesh进行前处理。网格采用四面体单元和六面体单元,以兼顾计算精度及运算效率,网格总数为274 856。依据表2分别设置各材料参数。
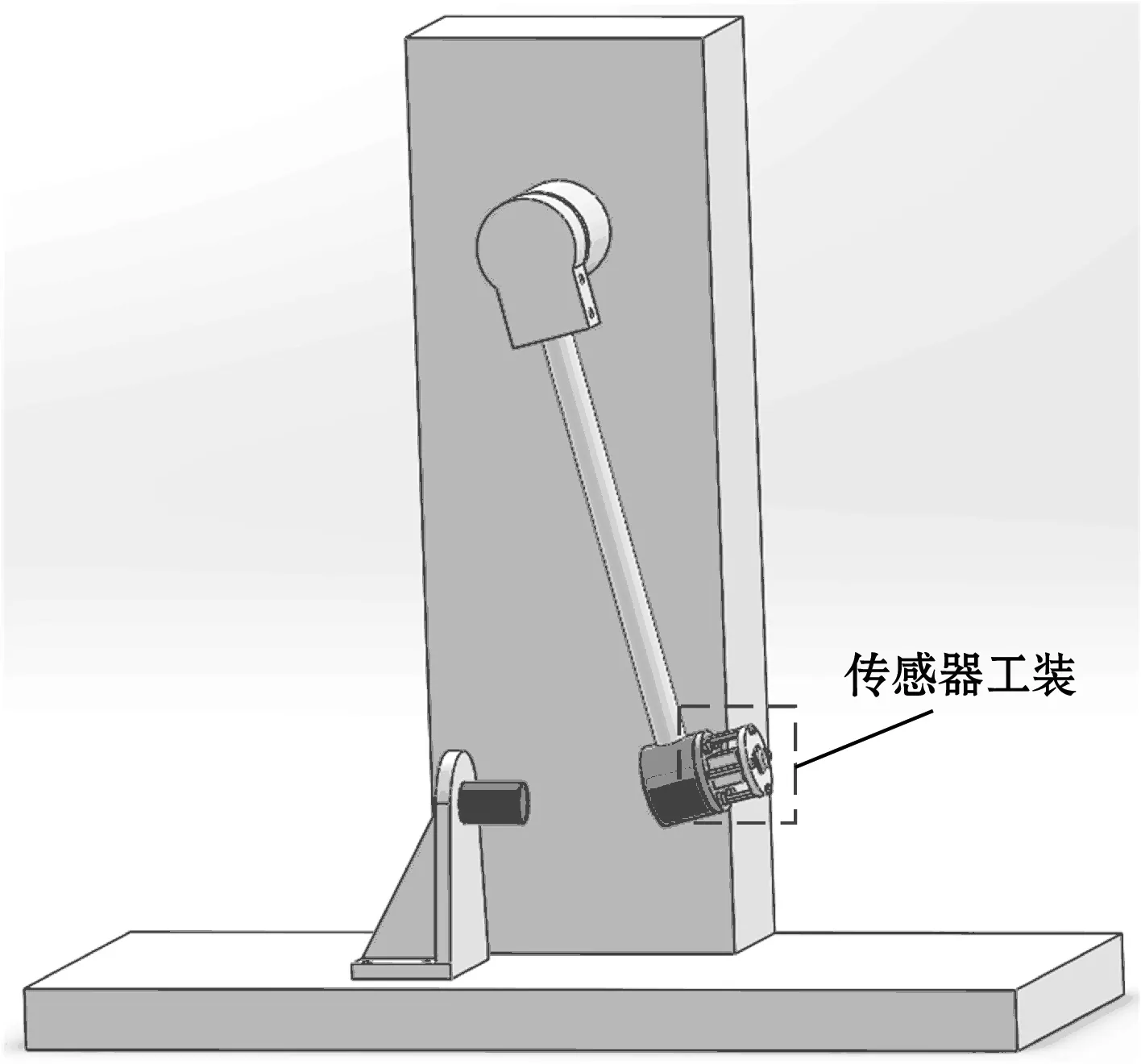
图6 冲击试验装置简化三维模型
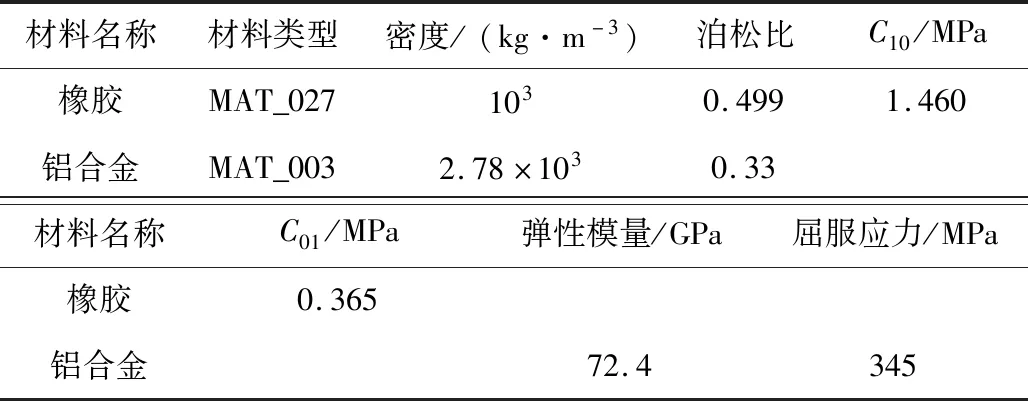
表2 仿真材料参数设置
仿真起始时刻为摆锤与波形发生器碰撞的瞬间,因此将摆锤模型置于贴近波形发生器的位置,如图7所示。摆锤初始冲击速度通过设置初始条件来实现。求解时间设置为20 ms,时间步长为0.1 ms。模型建立完毕后,将生成的K文件导入LS-DYNA求解器进行求解。
图7 摆锤位置示意图
将摆锤初始冲击速度分别设置为0.5、1、2、3 m/s进行仿真,得到不同初速度下摆锤冲击加速度-时间曲线如图8所示,以及MHD角速度传感器绕轴角速度-时间曲线,如图9所示。

图8 不同初速度下摆锤加速度-时间曲线(仿真)
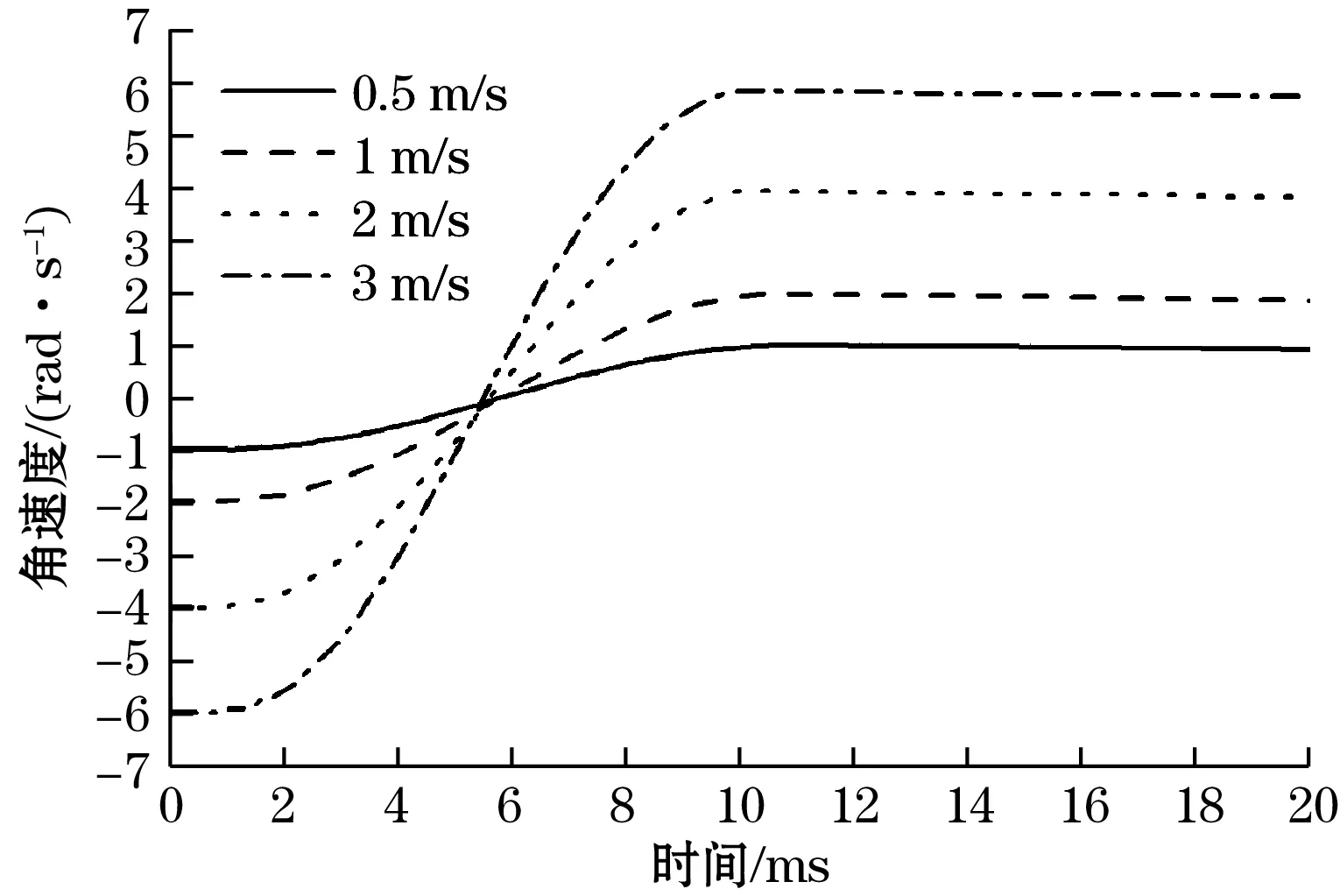
图9 MHD角速度传感器角速度-时间曲线(仿真)
将C10和C01设置为4组不同橡胶IRHD硬度对应的经验值(见表1),摆锤初速度设置为-1 m/s,其余参数保持不变进行仿真,得到不同硬度下摆锤冲击加速度-时间曲线如图10所示。
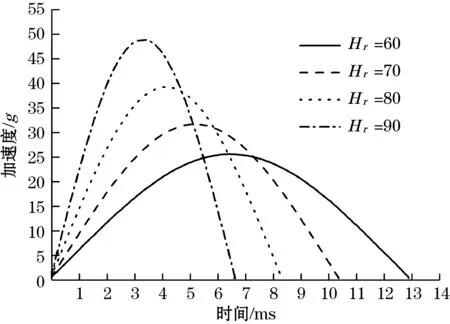
图10 不同硬度下摆锤加速度-时间曲线(仿真)
各组初始冲击速度以及橡胶硬度对应的计算冲击波形和仿真冲击波形数据如表3所示。
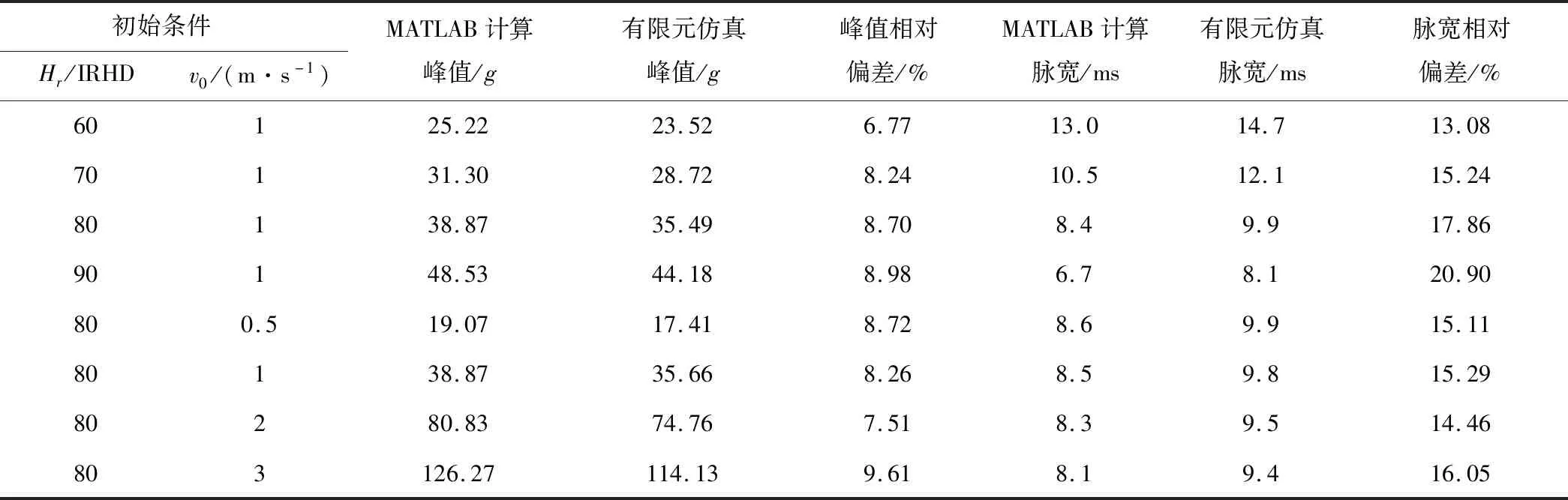
表3 计算冲击波形与仿真冲击波形对比
2.2 MHD角速度传感器输出电势数值计算及仿真
2.2.1 MHD角速度传感器输出电势数值计算
依据本文采用的MHD角速度传感器结构参数,由式(15)计算MHD角速度传感器标度因数为1.2×10-5V/(rad·s-1)。根据有限元仿真得到的不同摆锤初速度下MHD角速度传感器角速度-时间曲线,可计算得到MHD角速度传感器输出电势-时间曲线,如图11所示。

图11 MHD角速度传感器输出电势-时间曲线(计算)
2.2.2 MHD角速度传感器输出特性仿真
为了进一步探究MHD角速度传感器在冲击碰撞时产生的输出电势,采用基于有限体积法的流体计算软件Fluent对MHD角速度传感器进行仿真。
流体环模型的建立与网格划分在Ansys workbench中完成,材料属性依据MHD角速度传感器参数进行设置,网格结构选用四面体网格,总体网格数为24 960,所建立的模型如图12所示。

图12 流体环模型网格划分
在流体环模型计算中,Fluent关键部分设置如下:
(1)物理模型设置:经计算工作状态下导电流体的雷诺数小于1 000,采用层流模型。
(2)边界条件设置:流体环所有边界均设置为无滑移。
(3)区域条件设置:将上文有限元仿真所得的MHD角速度传感器角速度及线速度随时间变化曲线拟合为函数,写入用户自定义模块User Defied Function (UDF)文件中,设置整个框架的角运动和线运动。
(4)MHD模块设置:设置内外壁面导电,上下壁面绝缘,电流密度为0。定义外部磁场大小为0.1 T,方向沿Z轴正方向。
(5)迭代计算:时间步长设置为0.1 ms,计算步数为200。
经过Fluent数值计算,MHD角速度传感器在摆锤碰撞过程中的输出电势-时间曲线如图13所示。
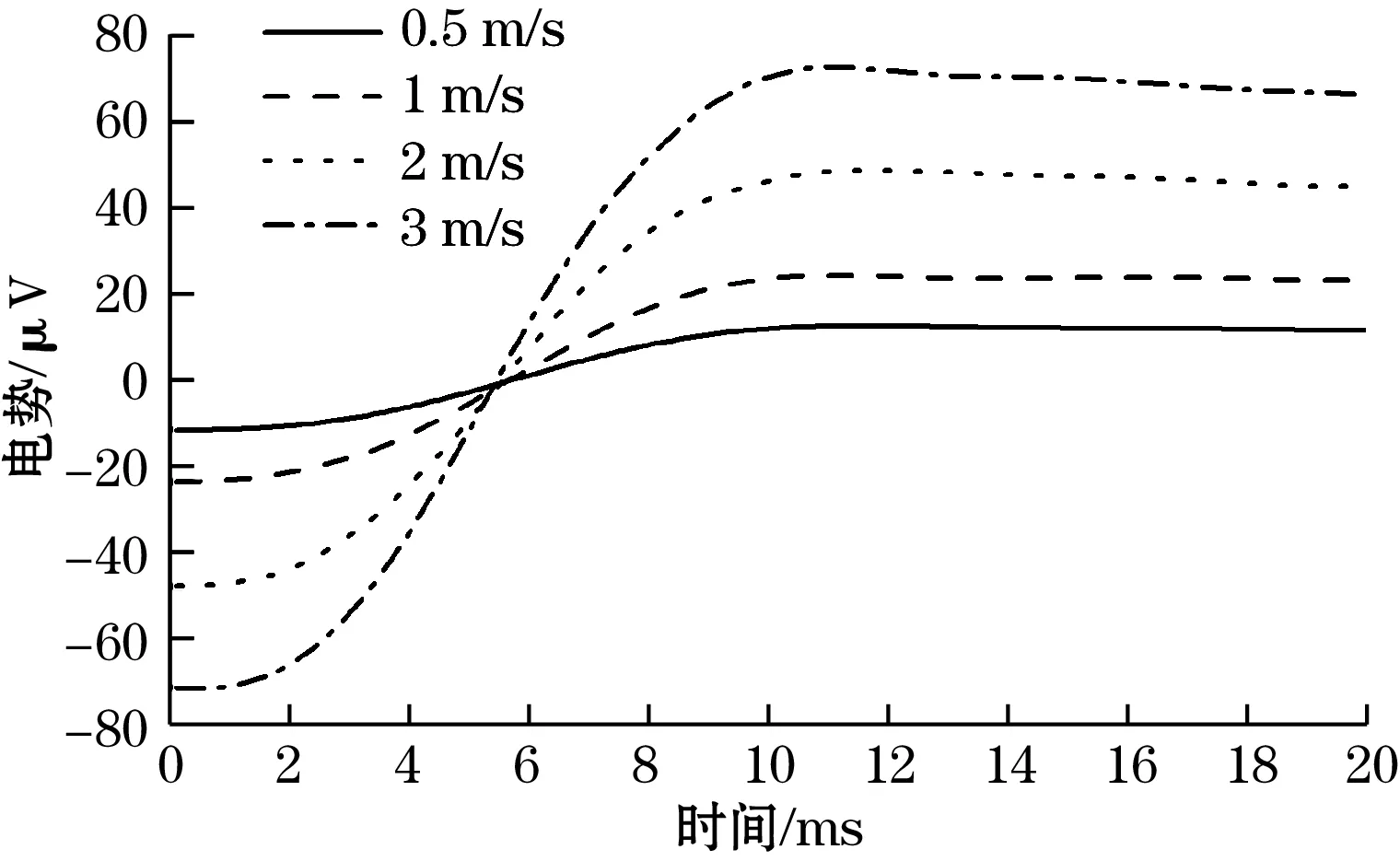
图13 MHD角速度传感器输出电势-时间曲线(仿真)
将MHD角速度传感器计算输出电势与Fluent仿真输出电势进行对比,如图14所示。

(a)v0=0.5 m/s
2.3 结果分析
(1)由表2可知,数值计算与有限元仿真冲击波形的加速度峰值偏差在10%以内,脉宽偏差在21%以内。随着摆锤初始冲击速度的增大,冲击波形的加速度峰值也增大,脉冲宽度略微减小。随着橡胶硬度增大,加速度峰值增大,脉冲宽度减小。两者在不同初始条件下的波形变化趋势一致。
(2)冲击试验装置产生的冲击波形满足提出的加速度以及角加速度的技术指标,计算与仿真结果对于试验装置的设计具有一定的参考意义。
(3)由图14可知,MHD角速度传感器计算输出电势与Fluent仿真输出电势基本一致,表明本文中的MHD角速度传感器可准确测量本文提出的冲击试验装置产生的冲击角速度。
3 结束语
文章基于MHD角速度传感器在汽车碰撞试验中的应用研究,设计了冲击试验装置。利用数值计算和软件仿真方法分析碰撞产生的冲击波形以及MHD角速度传感器的输出电势。该装置可产生加速度峰值为114.13g、角加速度峰值为2 238.24 rad/s2的半正弦冲击波形,符合冲击试验要求。MHD角速度传感器在冲击环境下标度因数为12 μV/(rad·s-1),与在非冲击环境下的标度因数一致,因此MHD角速度传感器的抗冲击性能较好。
