塑料冲击试验机摆锤形状对空气阻力的影响

韩志凌　田辉　王文成　王新华

(1．承德石油高等专科学校，河北 承德，067000；2. 河北省仪器仪表工程技术研究中心，河北 承德,067000；3．承德市精密试验机有限公司，河北 承德,067000)



塑料冲击试验机摆锤形状对空气阻力的影响

韩志凌1,2田辉1王文成1王新华3

(1．承德石油高等专科学校，河北 承德，067000；2. 河北省仪器仪表工程技术研究中心，河北 承德,067000；3．承德市精密试验机有限公司，河北 承德,067000)

塑料冲击试验机中摆锤形状影响空气阻力，进而影响摆锤长度计算结果的准确性。分析空气阻力计算的数学模型以及对摆锤侧板边缘截面分别为矩形、等腰梯形、三角形和椭圆形4种典型形状摆锤的空气阻力数值进行模拟，测定了摆锤的起始角与升角之间角度差，发现摆锤采用等腰梯形形状最合理，摆锤空气阻力随中部宽度、角度的减小而降低，但相对于中部宽度，角度对摆锤空气阻力影响更显著。

塑料冲击试验机摆锤空气阻力

按照国标GB/T 21189—2007规定，在塑料摆锤冲击试验机中，无试样时由摩擦引起的最大允许能量损失是冲击试验机的基本性能指标。为满足能量损失的要求，试验机制造厂家采取减小角位移传感器(或指针)、空气阻力(F)以及摆锤轴承摩擦等措施。在制作过程中发现，有些能量级的摆锤、摆锤形状所引起的F在能量损失中所占的比重较大，只有通过改变摆锤形状，才能使试验机满足最大允许能量损失的要求，因此，探讨不同摆锤形状对F的影响，对摆锤的设计有一定的指导作用。

1　F计算的数学模型及F对摆锤长度计算影响

1.1F计算的数学模型

在空气中运动的摆锤所受到的阻力，一般与摆锤迎风截面积、相对运动速度以及空气密度有关。由于流过摆锤的气流相对复杂，从理论上很难计算F的大小，可采用近似的公式计算F[1]，即：

F=ρv2CRA/2

(1)

其中：ρ为空气的密度；v为摆锤相对于空气的速度；A为摆锤迎风面积；CR为空气的阻力系数，与空气的速度、摆锤的形状有关，其数值难以确定。

1.2F对摆锤长度计算影响

F作为摩擦能量损失的组成部分，对试验机的影响较大。一方面，摩擦能量损失要符合GB/T 21189—2007中规定的最大允许能量损失要求；另外，F影响摆锤的振动周期(Tp)[2]，而摆锤长度(Lp)是通过测定摆锤在小振幅[摆动角度(θ)离开中心每侧应小于5°)下的Tp间接得到的，因此F也影响Lp计算结果的准确性，其说明如下。

Lp与Tp的关系如式(2)所示：

(2)

其中，g为当地的重力加速度。

而式(2)忽略了F的影响。如果考虑F，则摆锤的计算摆动周期(T1)为：

(3)

其中：I0为摆锤对摆轴轴线的转动惯量；lc为摆轴的轴线到摆锤重心的距离。

由式(3)可知，在其他条件相同的情况下，CR的大小影响摆锤的T1。CR越大，T1越大，而通过计时法计量的恰恰是摆锤的T1。因此，较小CR摆锤的T1的测量值[3]准确性大于较大CR摆锤的，进而使Lp的计算结果更准确。

为减小F，一方面可通过研发特殊结构的摆锤来实现，如整体式摆锤；另一方面，也可通过改变摆锤迎风部分的形状来加以实现。通常情况下，具有流线型外形的物体具有优良的流体静力动力特性。但在满足使用性能的前提下，应寻求有效较小F的简单形状，使成本不至于增加。

2　摆锤F数值分析

由于式(1)中的CR不易获得，因此摆锤所受的F难以通过式(1)计算得出。为获得F，采用数值计算法分析摆锤受力。

2.1计算模型及网格生成

现以11 J悬臂梁冲击试验机为例，其摆锤形状如图1(a)所示。为研究不同摆锤形状对F的影响，将摆锤的侧板边缘做成如图2所示的形状(图中实线所示)，模型1为标准的矩形截面，截面宽度为W；将矩形截面进行了倒角(α)处理，取α为60°，且中间部分的宽度(以下简称中部宽度，L)为5W/9，形成模型2所示的等腰梯形形状；在模型2的基础上补充一个三角形区域形成模型3所示的三角形形状；模型4采用端部椭圆化处理。由于锤头、锤杆等部分结构尺寸相同，因此在F的计算中不予考虑。

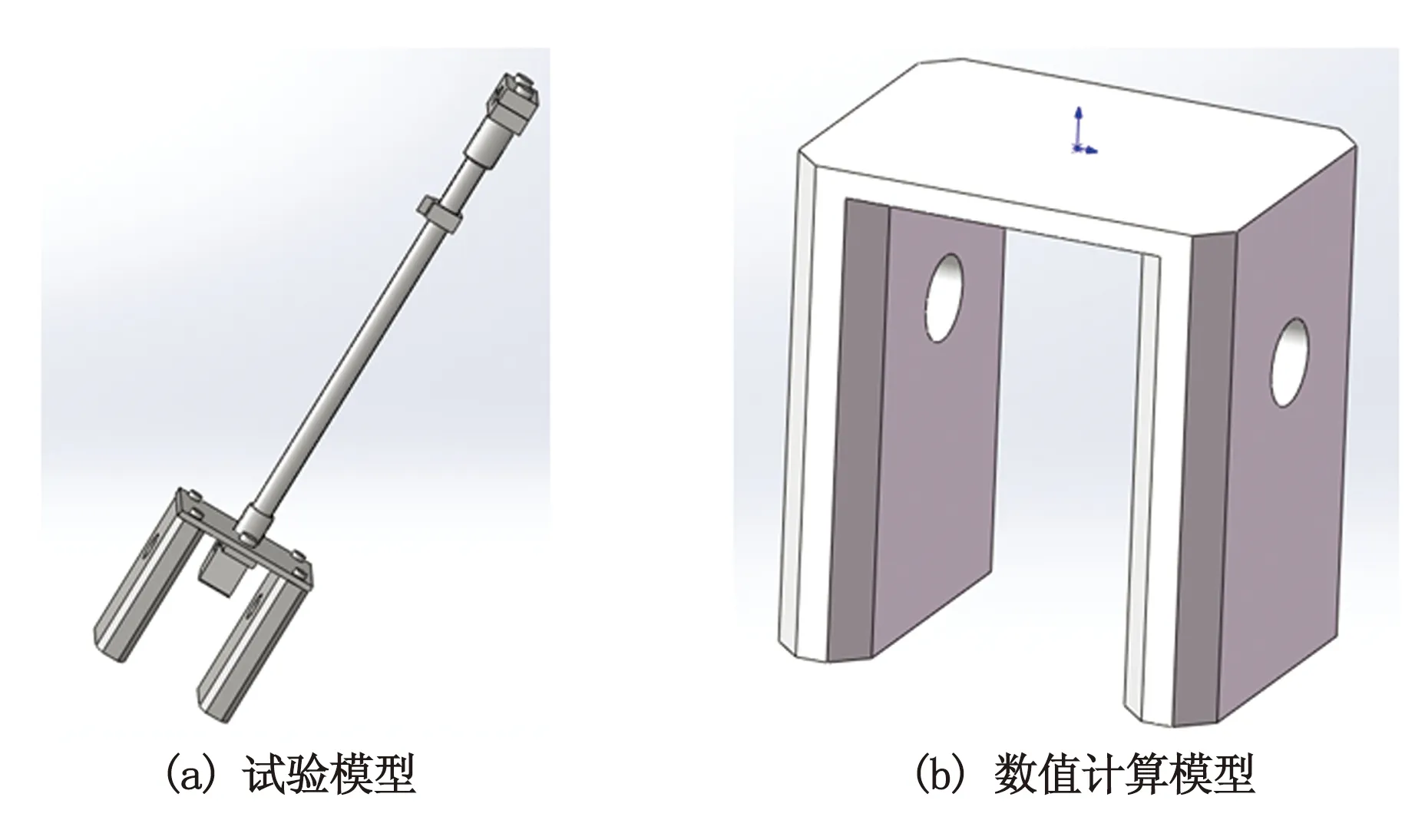
图1　 11 J悬臂梁摆锤

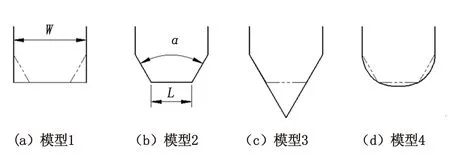
图2　摆锤侧板边缘形状模型结构示意

计算模型基于通过三维建模工具Solidworks以及数值计算前处理软件Gambit完成，计算模型如图1(b)所示，三维计算网格基于Size function[4]工具根据模型的不同介于45万～50万。

2.2 数值计算结果及分析

11 J悬臂梁冲击试验机的冲击速度为3.5 m/s，在模拟中，给定初始风速为3.5 m/s。通过对上述4个模型冲击过程风阻特性的数值分析，讨论不同形状摆锤对F的影响。图3(a)为截面为等腰梯形的摆锤在摆动过程中三维流场分布情况，红色区域为风压较高的区域。图3(b)，(c)中给出了摆锤摆动过程中典型结构前端压力及流线分布。由图3(b)可见，矩形结构前端高压区域较大，而来流遇到断面阻挡流动方向折转明显，在摆锤外侧形成了较大的漩涡区。由图3(c)可见，等腰梯形结构前段高压区域较小，来流可以很好地随等腰梯形流过，无明显的流动方向折转及漩涡。

图3　典型摆锤形状压力及流线分布

不同典型形状下F见表1，其中F为摆锤冲击过程中各面所受压力积分而得；并以模型1所受F为参考值，则其他3种情况的F可直观地表示为表3相对F(相对矩形截面的F)，即所求模型的F值与模型1的F值的比值。由表1可知，前端截面为等腰梯形形状(模型2)、椭圆形形状(模型4)的F相对接近，而三角形形状(模型3)的F最小，后3种模型均较矩形截面摆锤的F有显著的降低，然而3者间差距相差不大，均可作为摆锤横截面形状的优化方向。

表1　不同形状的摆锤对应的F及角度差

*摆锤由初始状态自由落下，测定的起始角与升角的角度差。

如果选择摆锤横截面形状为等腰梯形，并保持其W不变，为了进一步研究等腰梯形形状中α及L的变化对F的影响情况，分别做如下模型：1)固定L为W/3，分别设置α为120°，90°和60°，形成模型5、模型6及模型7；2)固定α为45°，分别取L为7W/9，W/2，W/3,0，形成模型8、模型9及模型10。采用相同的方法分别计算上述模型中F。

表2给出了等腰梯形α及L对F的影响。由表2可见,随着α的减小，F大幅降低。模型6的相对F较模型5的降低接近20%，模型7的相对F较模型6的降低约10%；而随着L的减小，F在一定程度上有所降低，但L的显著减小并未带来F的明显降低，例如模型10的相对F较模型9的降低在1%范围内。综上可知，与摆锤的L对F的影响相比，α对F的影响更大。

表2　等腰梯形α及L对F的影响

3　确定摆锤形状及试验法验证数值计算结果

从上述数值计算结果可知，采用三角形、等腰梯形和椭圆形的能量损失较小，矩形的能量损失最大。前3种模型的相对能量损失差距不大，均可视为摆锤的合理形状，但考虑到摆锤制作的工艺性，确定采用等腰梯形形状的摆锤。同时考虑到L，α对摆锤F影响关系，取L为10 mm，α为60°。

为验证数值计算结果的准确性，现通过试验法对图1(b)所示的摆锤形状进行F测定。试验用的冲击试验机采用欧姆龙E6B2-CWZ6C 1000P/R旋转编码器，实际摆锤形状如图1(a)所示，其锤头部分对应图2(b)所示。为模拟图2(a)，(c)，(d)所示的摆锤形状，采用摆锤边缘固定一个对应形状的硬塑料方式，并用502胶水固定在摆锤侧板上(图2双点划线表示摆锤的实际形状)。之所以采用在摆锤侧板加硬塑料方式进行试验，是因为硬塑料质量非常小，不会改变Lp等性能参数指标，试验数据之间具有可比性。试验中摆锤由初始状态自由下落，测定起始角与升角的角度差，其试验结果如表1中所示。

从表1的数据可知，等腰梯形形状摆锤的尺寸参数能够有效减小F，从而达到减小能量损失的目的。

4　结论

从上述的理论公式、数值模拟、试验数据分析可知，摆锤的结构形状及尺寸对F的影响较大。采用等腰梯形形状的摆锤不但能有效减小F，提高Tp的测量精度，使Lp的计算结果更准确，而且摆锤的制作工艺性好。因此，综合考虑F以及加工性能，发现摆锤形状为等腰梯形最为合理。其中，摆锤F随L,α的减小而降低，相对于中L，α对摆锤F影响更显著，故等腰梯形L取10 mm，角度α取60°是合理的。

[1]张天洋, 王艳辉, 曲光伟，等.空气阻力对复摆振动周期的影响[J].物理实验，2008，28(11)：42-45.

[2]韩志凌,王丽华,王新华,等.塑料冲击试验机整体式摆锤的研制[J]. 工程塑料应用,2013,41(9):78-82.

[3]杜月中,闵健,郭字洲.流线型回转体外形设计综述与线型拟合[J].声学技术, 2004,23(2):93-97.

[4]田辉. 离心泵内部流动数值计算及叶片型线优化设计[D].西安:西安交通大学.2008：1.

Effect of Pendulum Shape of Plastic Impact-Testing Machine on Air Resistance

Han Zhiling1,2Tian Hui1Wang Wencheng1Wang Xinhua3

(1. Chengde Petroleum College, Chengde,Hebei,067000;2. Hebei Province Instrument Engineering Research Center, Chengde,Hebei, 067000;3. Chengde Precision Testing Machine Co.Ltd., Chengde,Hebei, 067000)

The shape of pendulum in plastic impact testing machine affects air resistance,and then the accuracy of calculation results for pendulum length is affected. The mathematical model of air resistance is analyzed,and the numerical value about air resistance of four kinds of shapes of pendulum side plates such as rectangular, isosceles trapezoid, triangular, and elliptical are simulated. The angle difference between starting angle and lift angle of pendulum is tested. It is shown that the pendulum with isosceles trapezoid shape is the most reasonable. Air resistance of pendulum decreases with the reducing of middle-width and angle, meanwhile, cornpared with middle-width , the effect of angle is more significant on air resistance of pendulum.

plastics; impact testing machine; pendulum; air resistance

2015-06-26;修改稿收到日期:2016-04-18。

韩志凌，女，内蒙赤峰人，工程硕士，承德石油高等专科学校教授，主要从事优化理论等方面的教学和研究工作。E-mail：hanzhlcd@sina.com。

河北省科技计划支撑项目(11215654)，项目名称为仪器化非金属摆锤冲击试验机。

分析测试

10.3969/j.issn.1004-3055.2016.04.013