基于残差连接的Conv1D-BiGRU动态称重模型
2021-09-27史柏迪庄曙东江志伟
史柏迪,庄曙东,蔡 鸣,江志伟
(1.河海大学机电工程学院,江苏常州 213022; 2.南京航空航天大学,江苏省精密仪器重点实验室,江苏南京 213009; 3.梅特勒·托利多测量技术有限公司,江苏常州 213022)
0 研究背景及现状
在物流需求和劳动力缺口矛盾面前[1-2],动态称重技术是物流业发展的必然之路。在当前工业5.0与大数据模式下,复杂机电耦合系统的精确监控与状态预测[3-4]直接依赖于传感器实时返回的高维时序数据,但随之而来便是高维时序数据处理所带来的挑战。统计学回归[5]、全连接层DNN网络[6]、机器学习模型受限于模型特征,需将时序数据Flatten重组为1D数据进行处理,一方面忽略数据维度意义,且协同打包处理直接丢失采样信号的时序性,极大影响模型的监控与预测精度。
在动态测量中各压力传感器以1 024 Hz的速率进行信号采集,可将其改写为格式为Rn×t×s的数据,n为传感器数、t为时间维度、s为每秒采样频率,Hz。低速下传动稳定、压力信号平缓,使用DNN[7]或机器学习模型加权处理采样点信号便可精确输出质量。但在高速重载下,货物冲击[8]、电机振动及环境干扰[9](风力、空气对流、温度)等时序非线性干扰信号均被放大[10],此外,传感器信号经过滤波处理后依旧存在较大噪度。上述时序系统具有无序性与复杂度,使用传统DNN网络、机器学习类模型处理压力信号无法有效获取其时域与频域特性,最终加权输出精确质量。上述问题其本质为高维时间序列分析,因数据量大、维度高、且数据点之间的相互耦合,基于统计学、机器学习算法的模型无法有效进行分析处理。
近年来,国内外诸多学者一直致力于研究更优的时间序列预测方法。当前以CNN[11]、DNN、RNN[12]为主的深度学习模型因其强大的多元非线性拟合能力在复杂时序系统分析中有着广泛的使用。但在CNN、DNN中模型输出仅由当前时刻输入决定,破坏了数据的序列完整性。 RNN使用横向自展开结构建立了不同序列之间的联系,因此RNN网络在自然语言处理[13]、股票预测[14]等序列分析中有着广泛使用,但当输入数据维度较大、序列较长时,伴随着多次前向传播极易导致梯度消失[15]、模型超参数过多、梯度弥散等问题,最终导致模型难以训练。LSTM网络通过引入遗忘门、输入门和输出门式结构进行记忆限定,有效缓解RNN网络中”长期遗忘”问题,但与此同时也增大模型运算复杂度,且对高维数据预测精度依旧不佳。针对此问题,施行健[16]在2015年首次将CNN与LSTM模型相结合,提出ConvLSTM模型,通过输入以时间为维度雷达波形图便可以精确预测当地降水量。在ConvLSTM模型中,CNN[17-18]通过卷积池化抽取高维数据特征,有效降低高维数据的冗余问题,同时避免了高维数据直接输入DNN、RNN网络带来的维度灾难问题;为解决维度灾难问题,文献[19]在2018年提出三维卷积CNN与LSTM的组合模型,首次对视频内容进行了有效预测;在2019年,文献[20]提出GAN-LSTM模型,使用对抗神经网络(GAN)对卫星云图图片降维处理后输入LSTM网络实现了卫星位置的精确预测。上述时序模型均使用特定算法对高维数据特征提取后输入LSTM模型,最终预测精度良好。
参考上述模型,在本动态模型中为保留输入时间序列的信号特性,使用7个一维卷积网络(Conv1D)分别对4个压力与三轴加速度信号进行处理。此外,GRU模型作为LSTM模型的一种变体,通过将记忆门与输出门整合为重置门,在保证精度不变的前提下,降低了模型复杂度,使用BiGRU模型处理经一维卷积的高维信号。
1 试验设计与准备
测试系统由传动级(前)、TW155动态秤及传动级(后)组成,见图1,货物进入动态秤触发光电传感器时,压力与振动传感器开始采集数据,其采样频率为1 024 Hz。各传感器以及主要零部件装配图如图2所示。

图1 三级传动系统
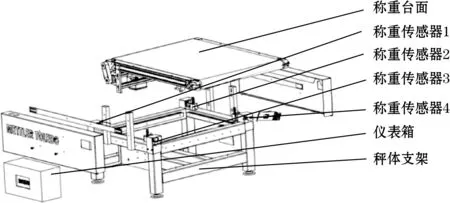
图2 TW155装配图
对测试货物使用高精度天平进行质量(m)检定依次为:1.004 1、5.124 9、19.978 4、30.074 1、49.997 1 kg,动态秤在静止时测量最大误差为0.015 kg,图2所示各压力传感器静态精度准确。设置带速v为120 m/min,动态下对各质量进行1 000次测定,将样本数据记录为式(1):
xi=[ax,ay,az,n1,n2,n3,n4]T
(1)
式中:i为样本索引(1≤i≤5 000);x为特定索引下的一个样本;a为加速度向量,a=[a1,…,as];n为压力向量,n=[n1,…,ns];s为采样信号长度,本模型中为128;训练样本集X=[5 000×7×128]。
此外,预留质量为40.478 4 kg的砝码,作为测试集。
2 信号一维卷积处理
2.1 信号相关性检验
为有效对加速度与压力信号进行相关性分析,在大小为[7×128]各组样本中,基于式(2)求解其合成平均加速度,并将压力信号改写为平均信号。
(2)
式中i为采样点索引(1≤i≤s)。
可将样本集降维为XDR=[5 000×2],基于皮尔逊相关性检验式(3)可直接求解其相关系数。
(3)
式中:N为样本数目;i为其索引;μn,μa依次为N个样本的平均压力与加速度信号。
计算得出其相关系数R为0.94,具有高度相关性,因此引入三轴加速度信号与压力信号共同作为输入可对动态测量系统进行更为精确的描述。
2.2 信号一维卷积处理
为有效获取信号特征,使用7个卷积网络分别对ax,ay,az,n1,n2,n3,n4进行处理,设输入层为传感器采集的信号向量,信号一维卷积层(Conv1D)位于输入层之后,若卷积核参数为向量k,则Conv1D操作可由式(4)表示。
(4)
式中:*为卷积符号;l为卷积核向量长度;xi为第i个输入特征(1≤i≤s-l);kij为第j个卷积核在输入xi对应的值;bj为其偏置;Relu为线性激活函数。
卷积层通过共享权值简化模型待训练的超参数,但当卷积核数目为u,对输入x将产生u种卷积输出,将增大运算复杂度。为化简运算卷积,卷积层后通常伴随着最大池化操作(MaxPooling)来提取并压缩特征,设采样大小为λ,其操作数学表达式可定义为式(5)。
maxdown(H,λ)=max{hi,i≤i≤iλ}
(5)
式中:maxdown为最大池化操作,H为由式(4)组成的输入向量。
经处理后,可将输入尺寸H压缩为原先的1/λ。信号分别进行3次卷积与2次池化处理,此外,为避免CNN网络产生退化现象,参考残差神经网络(ResNet[21])设置跨层连接,通过引入残差模块来避免深度网络的梯度消失问题,可得模型前向表达式(6):
out=F(x,W)+Wsx
(6)
式中:W为3次卷积与2次最大池化所包含的超参数;F为其对应前向传播处理;Ws为恒等变换所对应权重的矩阵。
结合式(4)~式(6)中依次对应的卷积、最大池化以及残差连接操作,则在卷积网络中各输入信号的前向传播流程如图3所示。
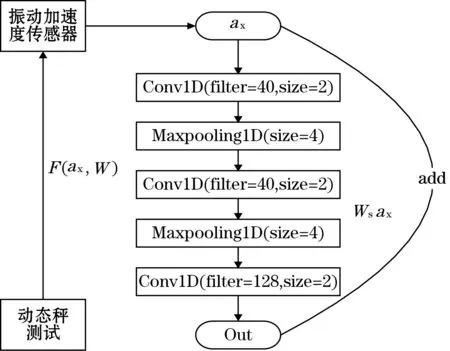
图3 ResCNN信号处理
图中,filter为滤波器的数目;size在卷积层中为卷积核的长度,在池化层中为采样大小λ。并且通过在卷积网络中引入跨层连接Wsax,使模型梯度着重于输入与卷积处理后的残差,有效缓解在传统深层VGG和AlexNet网络中因多次卷积池化带来的梯度弥散问题。
2.3 局部响应归一化(LRN)处理
为有效保证模型的收敛,设k、α、β为归一化调参数,基于局部响应原则使用式(7)处理最终网络输出值Out。
bi=outi/(M)β
(7)
式中:N为卷积过滤器的数目;n为相邻数据数。
基于复合求导计算可得模型误差E梯度传播如式(8)。
(8)
通过引入归一化调参数k、α、β,可有效在误差反向传播时对局部神经元引入竞争机制,输出权值比重较大的神经元,有助于模型快速收敛,并可抑制反馈较小的神经元来增强模型泛化性能力。
3 时间序列层BiGRU网络的建立
3.1 门控循环单元原理
门控循环单元(GRU)其结构如图4所示,通过引入更新与重置门来限定输入输出有效解决了循环神经网络(RNN)长期依赖问题。且相对于长短期记忆神经网络(LSTM)拥有更少的训练参数,模型更易收敛。
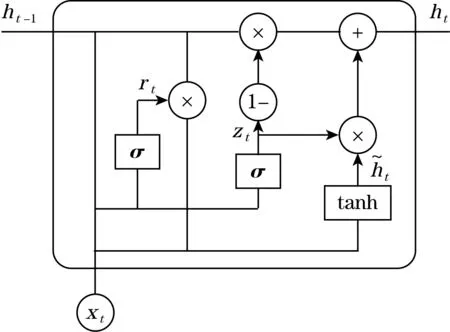
图4 门控循环单元
图中,xt为t时刻模型的输入;ht-1为t-1时刻隐藏层的输出,GRU单元通过式(9)~式(12)计算t时刻输出。
zt=Sigmoid(W(z)xt+U(z)ht-1)
(9)
rt=Sigmoid(W(r)xt+U(r)ht-1)
(10)
(11)
(12)
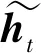
3.2 BiGRU序列层的建立
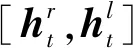

图5 BiGRU结构
图中,GRU单元即为如图4所示结构;i为样本序列索引,若k为步长则会产生n(s-k+1)个BiGRU序列输入与输出。GRU(L)、GRU(R)依次为正向与逆向门控循环单元。
最终为进一步强化模型非线性拟合能力,对BiGRU所产生的n个输出将其送入神经元依次为64、1的2层DNN网络加权处理。综上可以得到Conv1D-BiGRU模型处理流程图如图6所示。
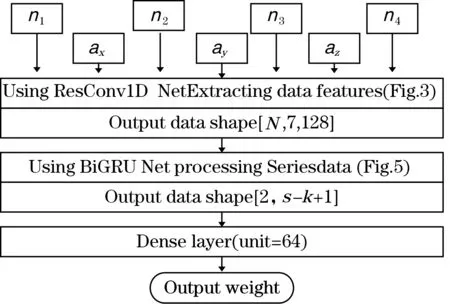
图6 Conv1D-BiGRU模型
图中,ax,ay,az,n1,n2,n3,n4依次为图2中各传感器返回信号。N为训练集样本数目;s为采样点数目,k为步长,即GRU单元所读取数据点数;最终模型待训练超参数为137 754。
4 Conv1D-BiGRU模型性能测试
4.1 模型训练
选用最大误差errmax、平均绝对误差mae、方差std作为性能评价指标:
errmax=max{erri},err=y-f(x)
(12)
(13)
(14)
式中:y为货物真实质量;f为Conv1D-BiGRU的前向传播处理;x为传感器返回的压力与振动信号。
指标std在5个质量级中分别测定,测量模型在同一质量下的稳定性与收敛能力。
对5 000个样本进行分层随机抽样,5个质量点各自抽取800个样本作为训练集,余下为验证集验证模型泛化性误差,使用Adam算法优化器,设置迭代次数为200进行模型训练。此外,为保证梯度损失的稳定传播使用均方误差(MSE)作为损失函数,图7为训练集与验证集波动曲线。
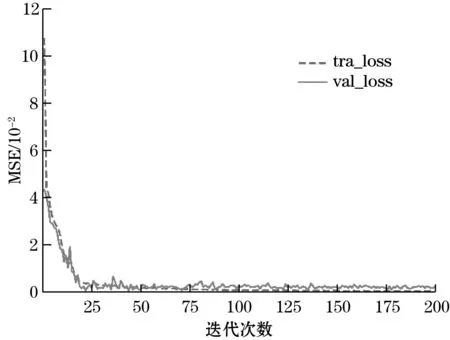
图7 模型训练
图中,随着迭代进行,训练集与验证集均方误差同步下降,最终训练误差(val_loss)为4.314×10-4,验证集当迭代次数(t)大于100时,误差稳定收敛于区间[6×10-4,7×10-4],Conv1D-BiGRU模型已经有效训练。
此外,为证明突出Conv1D-BiGRU性能的优越性,在计算机配置为CPU(i7 9750h)、RAM(32 GB)、GPU(GTX1660Ti),编译环境为python(3.7.5)、keras(2.2.4)的背景下使用Nvdia cuda进行GPU加速运算。CuDnn版本为7.1.1,cuda版本为9.1的条件下,同步训练了经Cov1D处理后进行堆叠操作的BP、BiLSTM、BiRNN模型,表1中对各模型在1 000个验证集样本中的性能表现进行了记录。
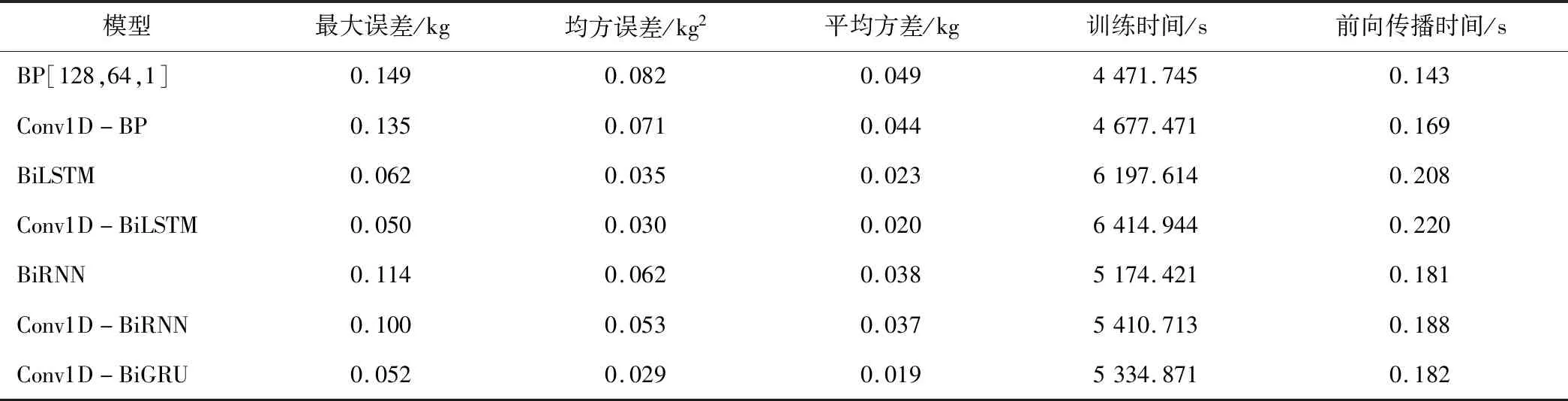
表1 模型性能对比
表1中,BP[128,64,1]为各隐藏层神经元数为128,64,1的误差反向传播网络。综合各模型验证集表现,可知经过Conv1D处理提取高维特征输入模型时,可以较小的时间复杂度为代价,来有效提高模型称重预测精度。此外,在本模型中,Conv1D-BiGRU与Conv1D-BiLSTM模型预测误差几乎一致,但BiGRU因化简了门控单元故有着更小的时间复杂度。综上,Conv1D-BiGRU有着最优的性能表现。
4.2 模型测试
使用上述训练完成的卷积网络模型,在传动系统中使用与训练集样本不相关,质量为40.478 4 kg的圆盘砝码,在带速135 m/min下进行200次质量检定,表2对各模型实际工程误差进行了记录。
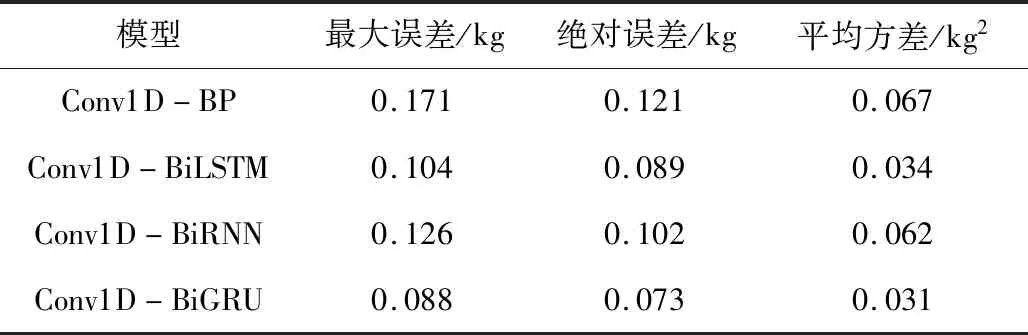
表2 模型测试性能对比
表2中,测试集误差虽较验证集误差(表1)有所放大,但各模型误差范围基本可控。且在实际工程使用过程中,Conv1D-BiGRU模型有着最小的最大误差与平均绝对误差,且方差较小数值波动可控,所以该模型有着最佳的动态称重精度。
5 结束语
(1)设计了采用残差连接的一维卷积网络处理各传感器信号,经实验对比,较传统循环神经类网络与全连接层网络可以获得更好的动态称重精度并有效抽取信号的高维特征。
(2)验证集样本表明,BiGRU模型训练时间复杂度与BiRNN一致,性能也与BiLSTM模型基本持平。
(3)使用改进的Conv1D-BiGRU模型处理来自ax,ay,az,n1,n2,n3,n4传感器信号时,可以在动态模式下实现货物质量的精确测量,并且当工况改变时模型泛化性良好。
