基于MBN检测的励磁控制及波形校正

狄静宇，何存富，刘秀成，李永春

(1.北京工业大学材料与制造学部，北京 100124；2.台湾成功大学机械工程学系，台湾台南 70101)

0 引言

磁巴克豪森噪声(magnetic Barkhausen noise，MBN)对于铁磁性构件的表面硬度、残余应力和塑性变形等力学性能的变化敏感，可用于铁磁性材料力学性能的快速检测和评估[1-4]。目前，国内、国际上对于MBN检测没有一个通用的实施标准，不同检测系统和探头得到的结果无法直接进行对比[5-8]。主要是由于检测过程中，激励磁场强度和波形会受到多种因素影响，如不同磁路结构、不同励磁参数、提离距离波动、传感器倾角改变以及不同的磁轭材料的非线性磁特性等[9]。因此，实现激励磁场强度的稳定控制和激励磁场波形的畸变校正对于实施MBN检测的标准化和实现不同MBN检测系统结果的直接对比是非常必要的。

Birkelbach等[10]通过设置比例控制器，采用模拟电路负反馈算法进行波形校正。Bertotti[11]和Matsubara[12]等针对特定的励磁结构，实施了数字波形校正。White等[13-14]运用数模结合实现了激励磁场强度的稳定控制，但是控制算法比较复杂，不便于硬件的实现。Stupakov等[15-16]基于LabVIEW软件进行磁场幅值、磁场偏置和磁场波形的反馈控制和校正，从而实现可控励磁。Chatziilias[17]等采用谐波补偿数字反馈控制进行波形校正，但只适用于波形畸变较小的软磁性材料。Zurek等[18]利用自适应数字反馈控制算法进行波形校正，但该算法的控制速度较慢。

激励磁场强度的变化会改变MBN幅值，造成检测结果很大的误差[19-20]。激励磁场波形的畸变是由于高次谐波的产生，畸变会造成磁场基波能量的损失，从而影响MBN无损检测的精度要求。本文从激励磁场强度稳定控制策略和波形校正方法的角度，基于MATLAB/Simulink进行计算机动态仿真实验，验证该系统设计的可行性[21-22]。该研究可为实现不同MBN检测系统之间的直接对比以及MBN检测的标准化实施提供借鉴；同时可在一定程度上降低检测过程中多种因素对励磁的影响。

1 闭环控制理论与模型

磁巴克豪森噪声检测多为静态开环模式的无损检测，即检测过程中试件与传感器探头的位置不发生相对变化，并且对激励磁场的强度和波形不进行反馈控制和校正。首先考虑检测系统的基本组成，一般由信号发生器、功率放大器、磁巴克豪森噪声传感器、霍尔元件以及信号采集卡等组成，如图1(a)所示。其中与磁场激励系统相关的为信号发生器、功率放大器和磁巴克豪森噪声传感器的励磁轭铁；为了对激励磁场强度进行稳定控制和对激励磁场波形进行畸变校正，需要引入闭环负反馈控制信号，该信号可由霍尔元件或置于试件表面的闭合线圈获得，负反馈控制系统设计的目的就是对该信号强度进行稳定控制和波形的畸变校正。

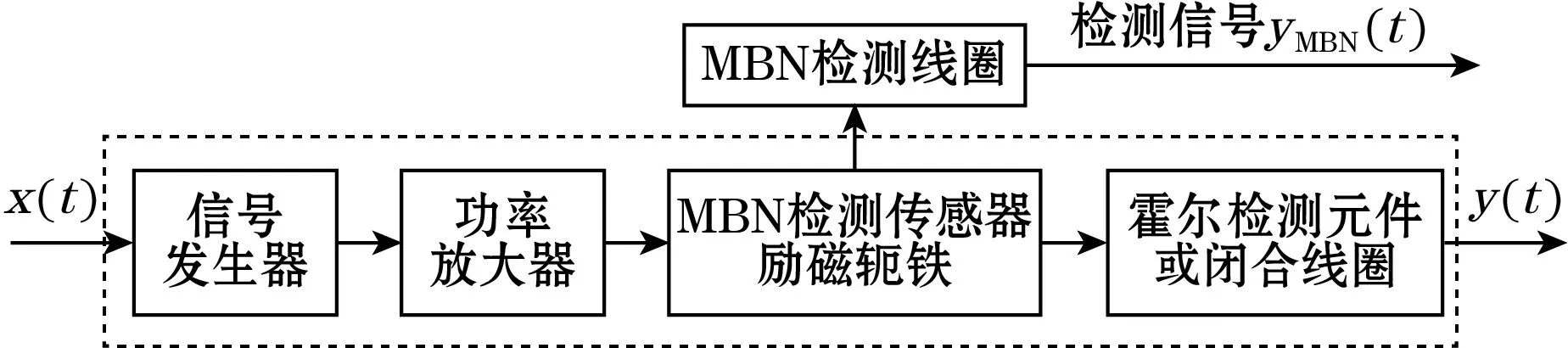
(a)

由于该检测系统不含机械、液压等动力传递过程，因此进行系统设计时可将该系统近似为一阶滞后系统，如图1(b)所示，一阶滞后系统的传递函数为

(1)

式中：T为系统时间常数；A为放大系数。

在进行磁巴克豪森噪声检测的过程中，一般设定信号发生器的原始输入信号为标准正弦信号，对于系统的激励输入信号：

x(t)=usin(ωt)

(2)

该标准正弦信号经过一阶滞后环节后的系统输出信号为

(3)

可见，系统的输出响应为一个快速衰减的瞬态分量和一个同频的正弦稳态分量，根据输入信号和稳态输出信号可以确定该一阶滞后系统的模型参数。对于本研究中，设定输入信号为x(t)=sin(2πt)；设定输出信号为y(t)=5sin(2πt-π/6)；计算得到系统参数为：T=0.1 s，A=5.8。

PID控制器即基于偏差信号的比例-积分-微分控制器。PID控制算法简单，具有很强的鲁棒性，可靠性高并且便于工程上的实现；因此直到现在很多闭环反馈控制回路仍选用这种控制算法，PID控制器的传递函数为

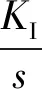
(4)

通过对KP、KI和KD的合理整定，可以实现快速、稳定并且无静态误差的负反馈控制系统设计。对于激励磁场的波形校正就是对产生的高次谐波进行抑制，从而降低波形信号的畸变程度；评价激励磁场信号的畸变程度，引入畸变因子表达式：

(5)

式中：K为畸变因子；U1为基波信号幅值；Ui为二次及以上高次谐波信号幅值。

对于奇谐信号产生的高次谐波以奇次谐波为主，因此在系统输出端引入3、5和7次谐波信号为：

y3rd(t)=sin(6πt)

y5th(t)=0.2sin(10πt-π/10)

y7th(t)=0.04sin(14πt+π/10)

该系统的设定输入信号、设定输出信号和系统开环输出信号如图2所示。对于激励磁场的强度控制，引入信号强度有效值的概念：

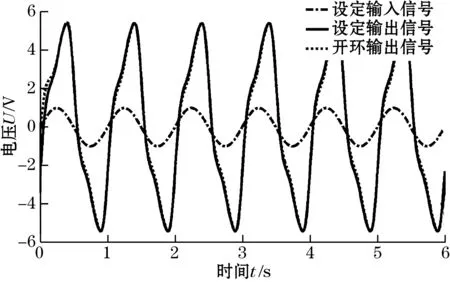
图2 系统的设定输入信号、设定输出信号和开环输出信号

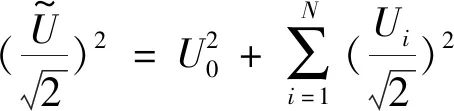
(6)

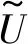
对于上面设定的谐波信号，可求得信号初始畸变因子为K=0.204 1，信号初始强度为r0=5.103 1 V，该初始强度作为参考控制输入。

2 系统设计与计算机动态仿真实验

2.1 激励磁场波形畸变校正

不同磁轭材料的不同非线性磁特性会造成激励磁场波形发生不同程度的畸变，比如由铁氧体材料制作的磁轭，其励磁波形畸变因子为8%左右；而由硅钢片材料制作的磁轭，其励磁波形畸变因子为1%左右，激励磁场波形的畸变会影响MBN检测的结果[23]。为了提高MBN检测的精度和实施MBN检测标准化等方面的需求，对激励磁场波形进行畸变校正是必要的。本研究从系统设计的角度，基于MATLAB/Simulink进行计算机动态仿真实验，验证该系统设计的可行性，图3给出了激励磁场波形畸变校正的Simulink模型。

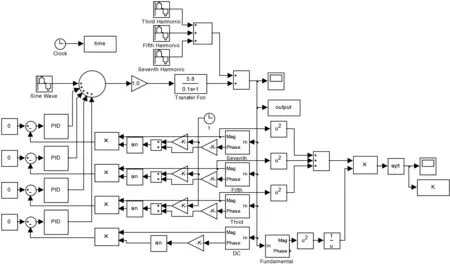
图3 激励磁场波形畸变校正的Simulink模型

图4给出了励磁波形畸变校正前后的波形对比图，结合图5所示畸变因子的定量变化曲线图，畸变因子由初始的20.41%降到5.28%；可以看出利用PID控制算法可以有效抑制高次谐波的产生，从而可以有效对励磁波形的畸变进行校正。图6为励磁波形畸变校正过程中直流分量的变化情况，可以看出对于基频为1 Hz的励磁信号经过6 s左右，即6个周期左右的动态调节，整个负反馈控制过程趋于稳定，直流分量消失。

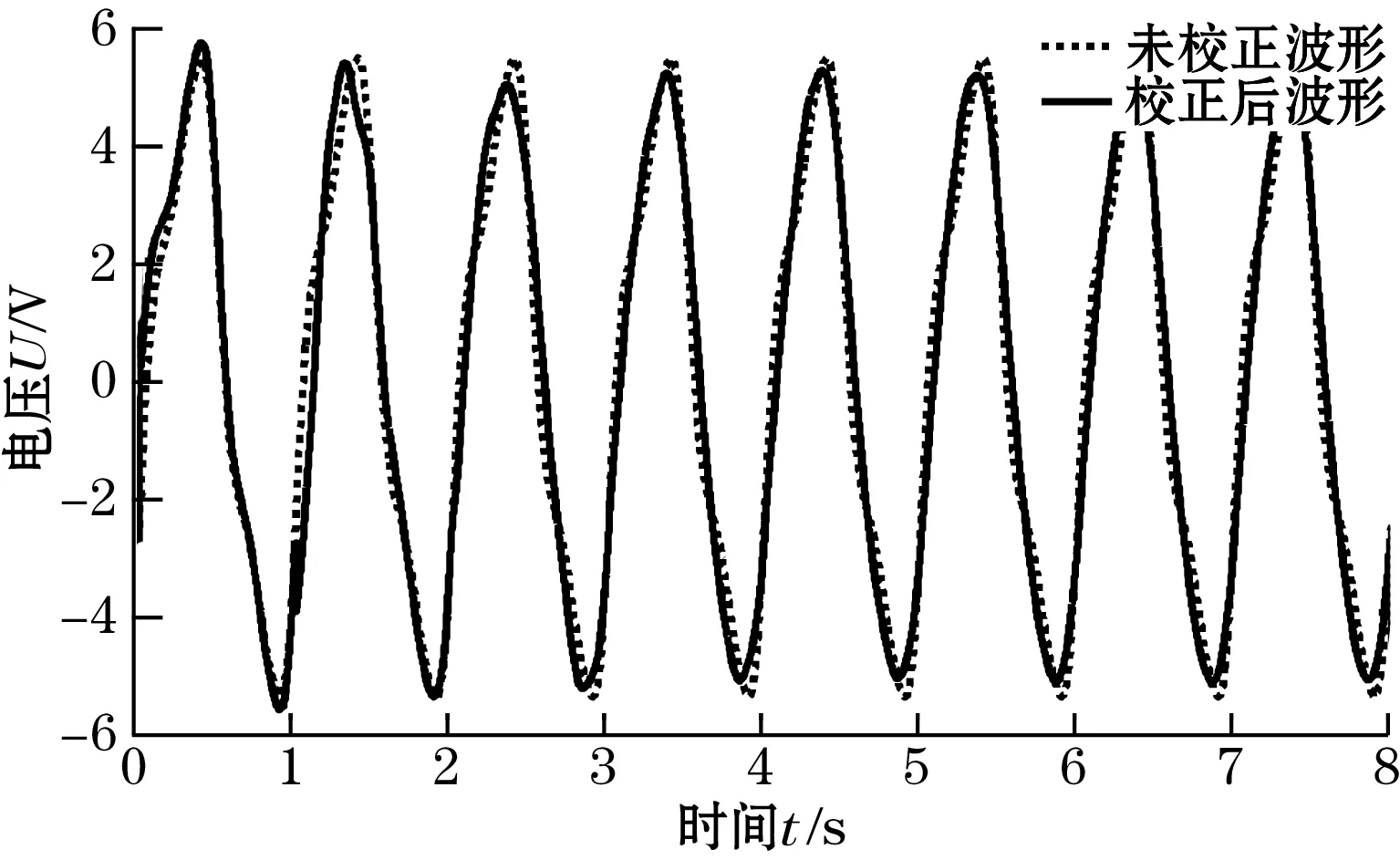
图4 励磁畸变校正前后波形的对比图

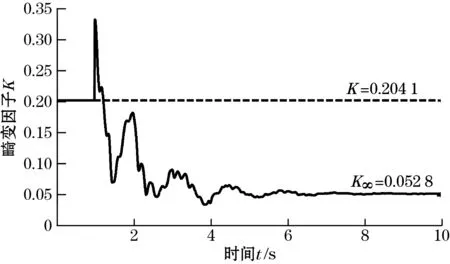
图5 畸变因子的定量变化曲线图

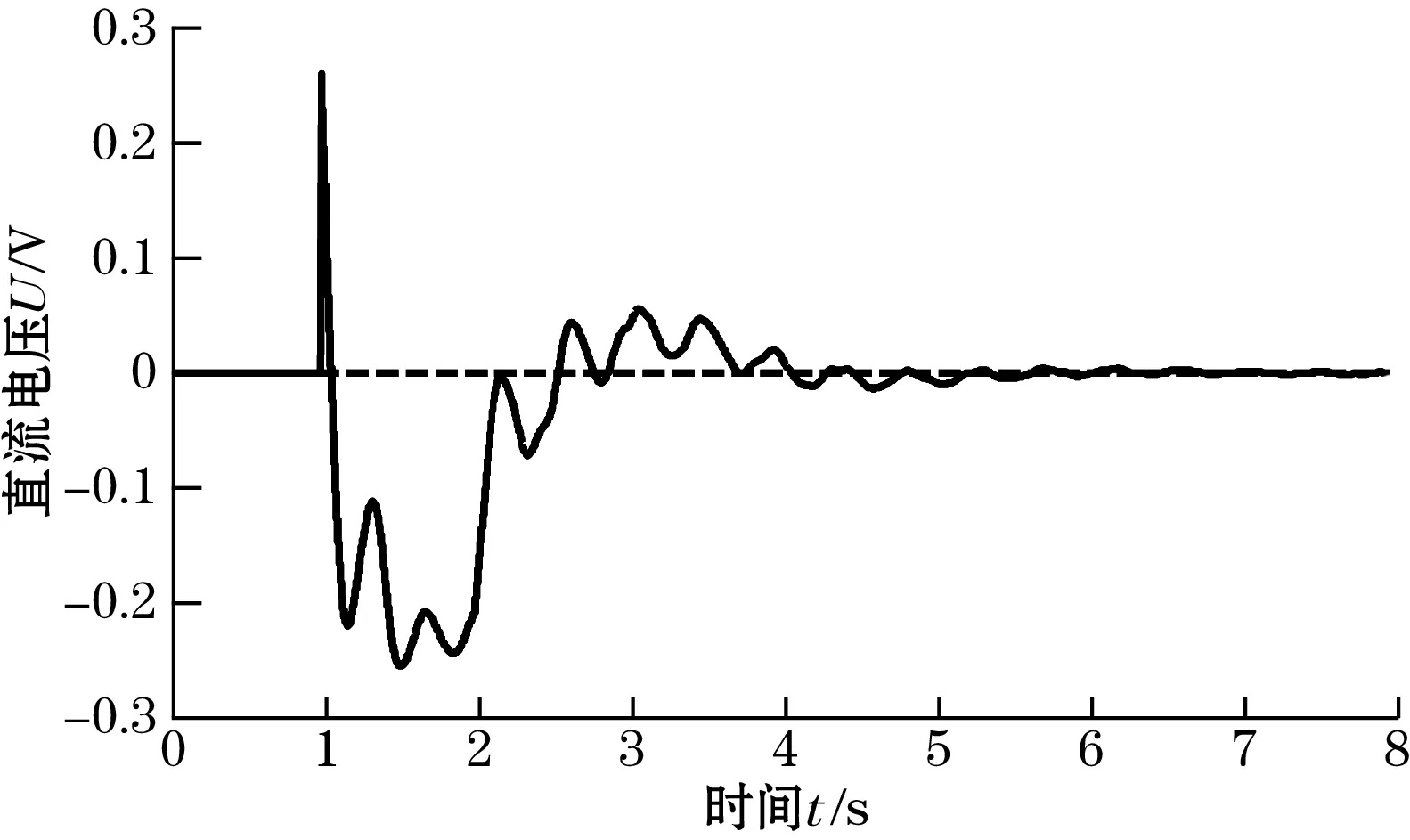
图6 励磁波形畸变校正过程中直流分量的变化情况

2.2 激励磁场强度稳定控制

在MBN无损检测的实施过程中，常由于某种原因使得施加在试件上的激励磁场强度的大小发生变化，比如提离距离的波动、传感器的倾角改变等；因此对激励磁场强度进行稳定控制是必要的。本研究基于MATLAB/Simulink进行负反馈控制系统设计，励磁初始强度为r0=5.103 1 V，以该初始值作为系统参考控制输入。搭建励磁强度稳定控制的Simulink模型如图7所示，在进行计算机动态仿真过程中，以前述等效电压幅值公式(6)作为激励磁场强度的定量描述，并且以此信号作为负反馈控制信号。

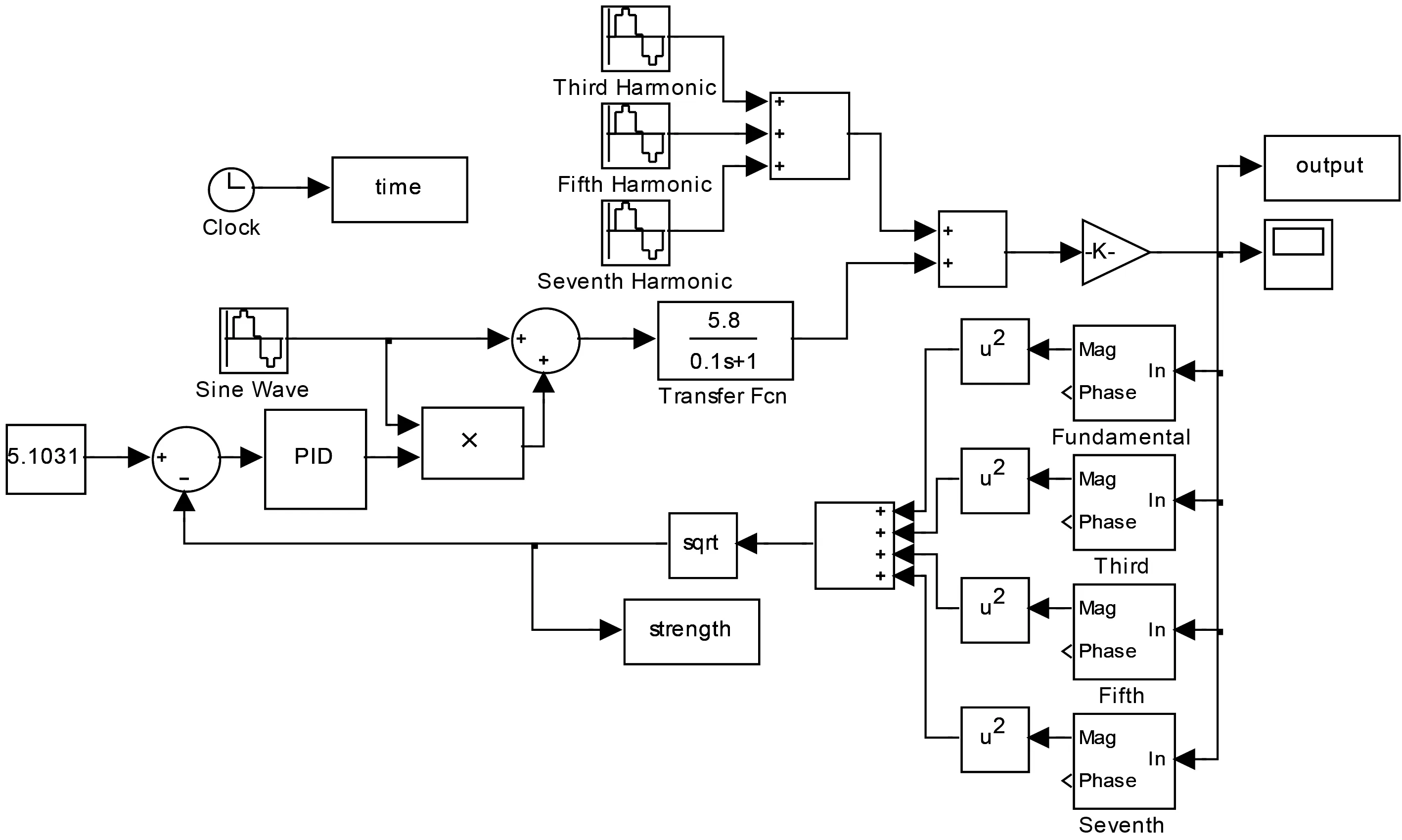
图7 激励磁场强度稳定控制的Simulink模型

如果分别设定激励磁场强度增大为初始强度值的1.4倍，即1.4r0=7.144 3 V，和设定励磁强度减小为初始值的0.6倍，即0.6r0=3.061 9 V；经过PID控制器得到的励磁强度稳定控制波形分别如图8和图9所示，图10和图11为动态调节过程中励磁强度的定量变化曲线图。

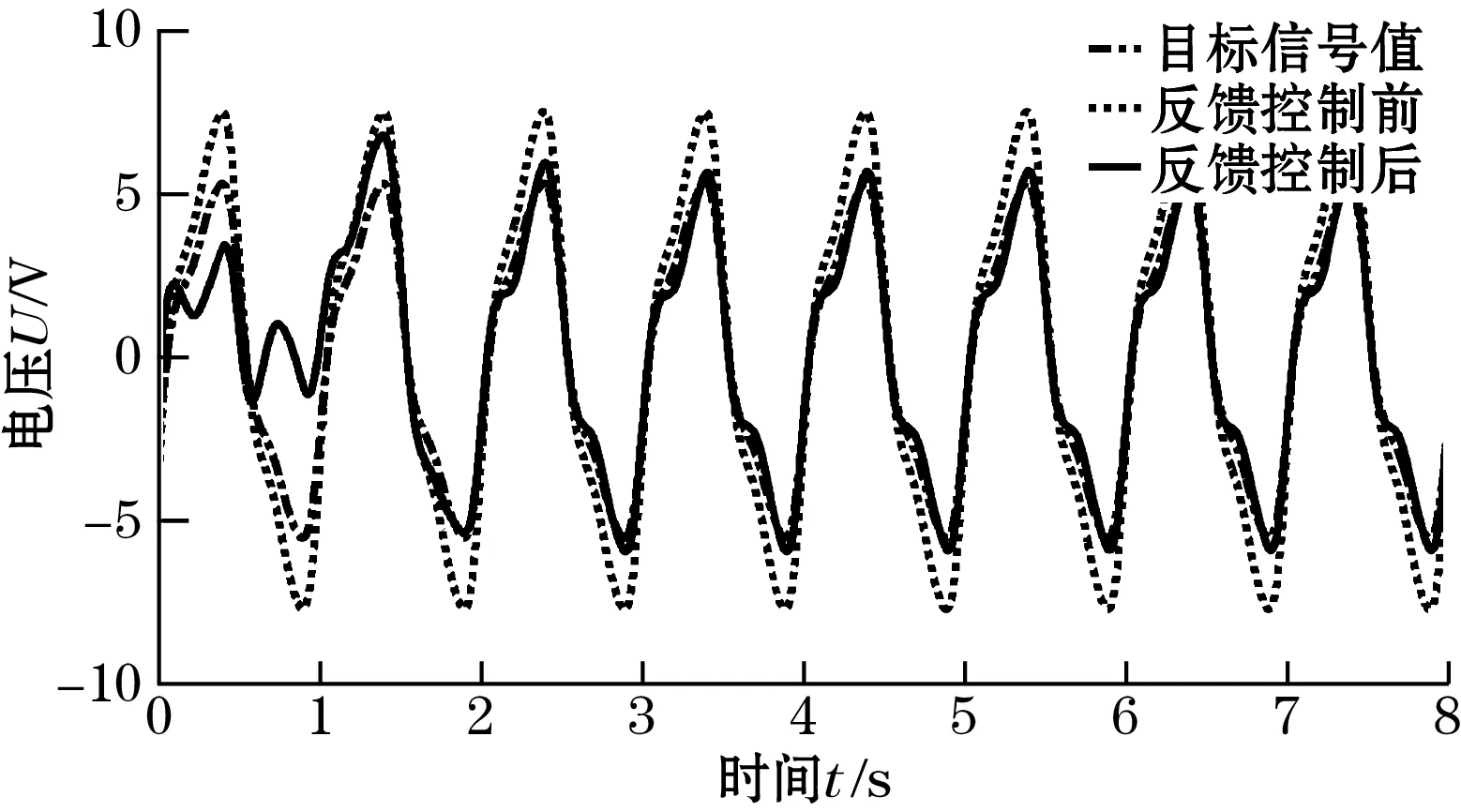
图8 激励磁场强度变大的强度稳定控制波形

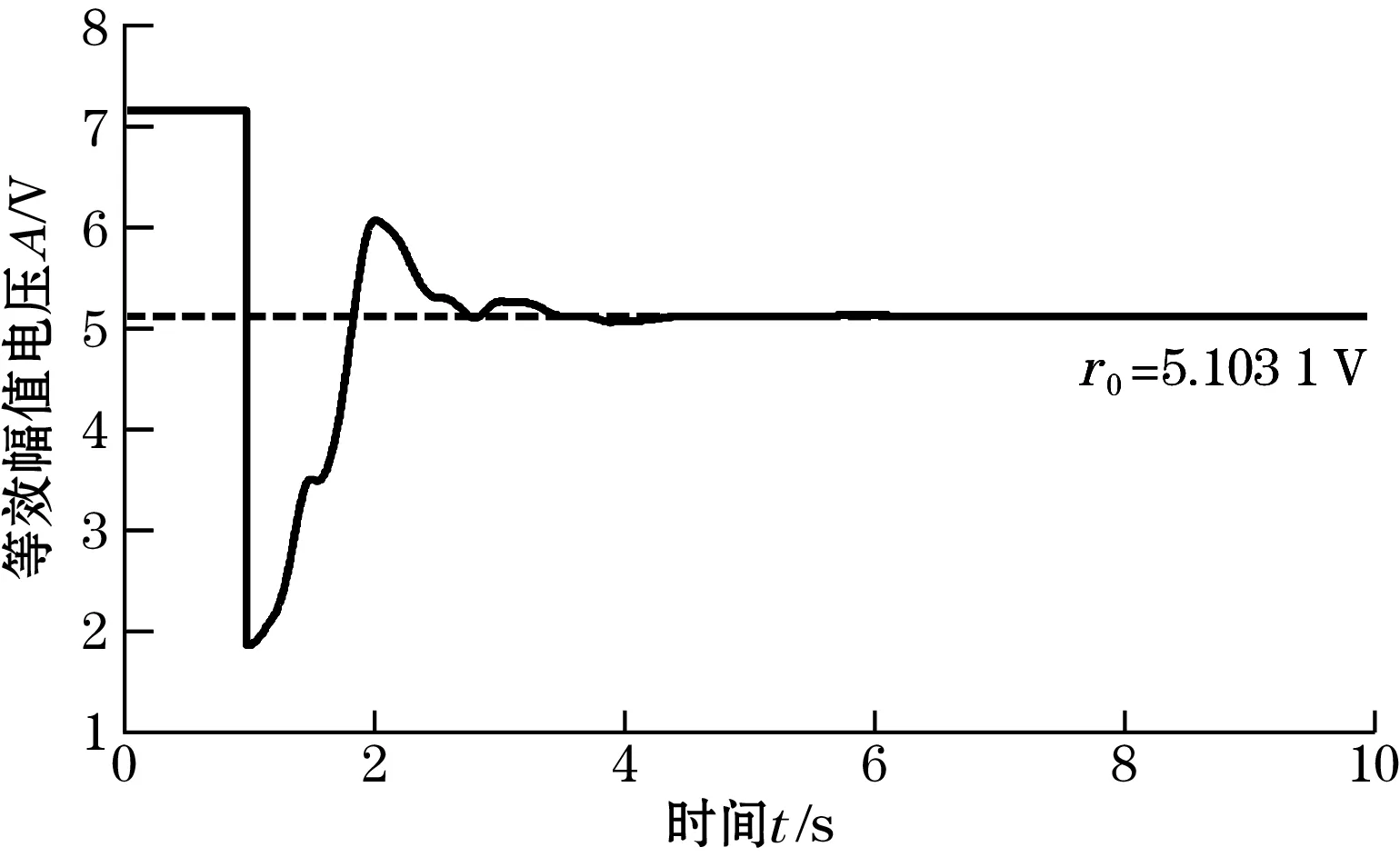
图9 激励磁场强度的变化曲线图1

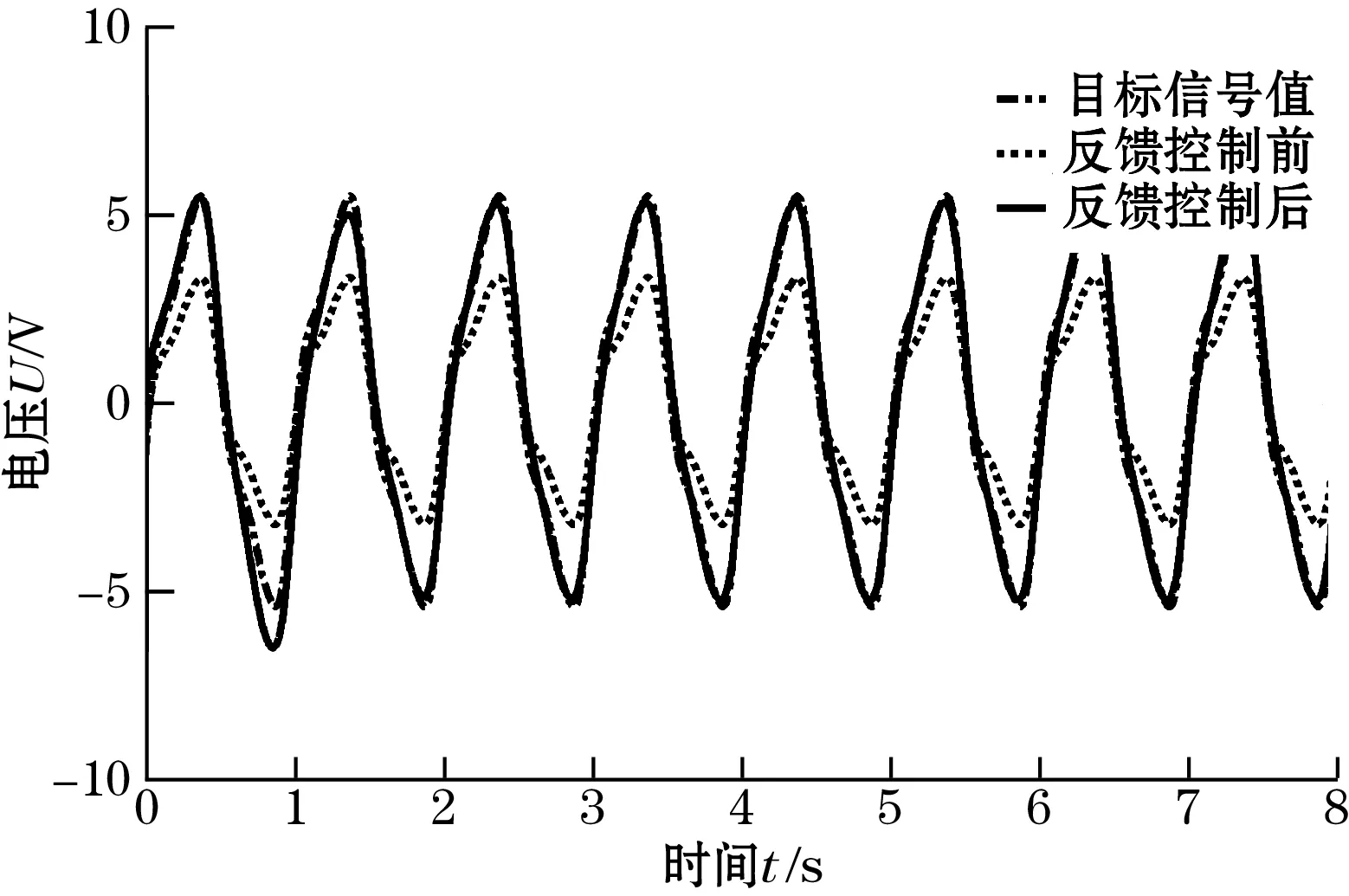
图10 激励磁场强度变小的强度稳定控制波形

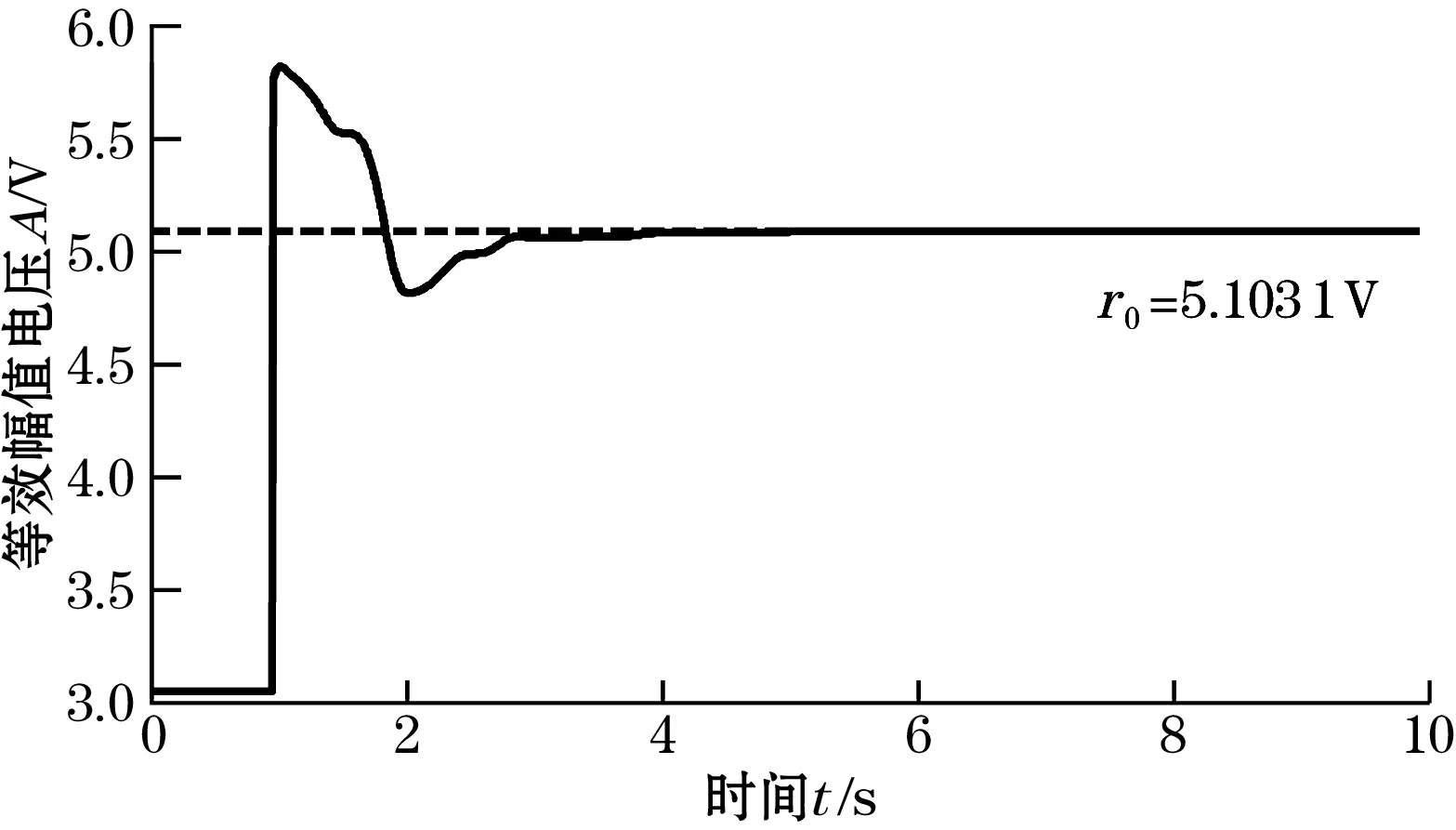
图11 激励磁场强度的变化曲线图2

从这两个例子可以看出，应用PID控制器可以很好的对激励磁场的强度进行稳定控制，控制过程快速、平稳并且无静态误差。经过大约5个周期的动态调节过程，整个负反馈控制系统趋于稳定，激励磁场强度稳定保持在初始强度值r0。

2.3 同时实施波形畸变校正和励磁强度稳定控制

在很多情况下，激励磁场的波形畸变和强度的不稳定是同时存在的，因此需要同时实施励磁波形畸变校正和励磁强度稳定控制。因此同时进行励磁波形畸变校正和励磁强度稳定控制的双闭环负反馈控制系统设计是非常必要的，图12给出了搭建的双闭环负反馈控制系统Simulink程序模型框图。

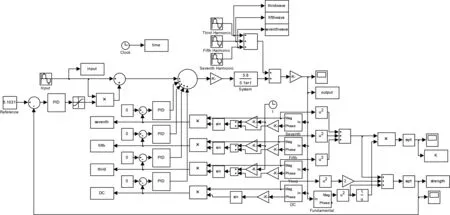
图12 同时实施励磁波形畸变校正和励磁强度稳定控制的Simulink模型

图13～图16为励磁强度增大为原来的1.4倍的励磁强度稳定控制和励磁波形畸变校正同时实施的仿真结果；结果显示经过7个周期左右的动态调节时间，PID负反馈控制系统趋于稳定，直流分量消失，波形畸变因子由初始的20.41%降到6.44%，激励磁场强度稳定保持在初始强度值r0。

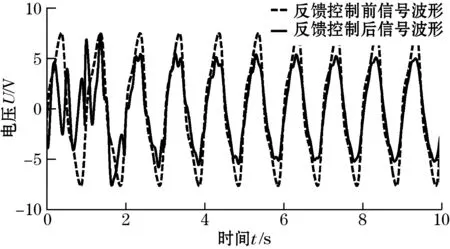
图13 激励磁场的波形对比图(励磁强度增大时)

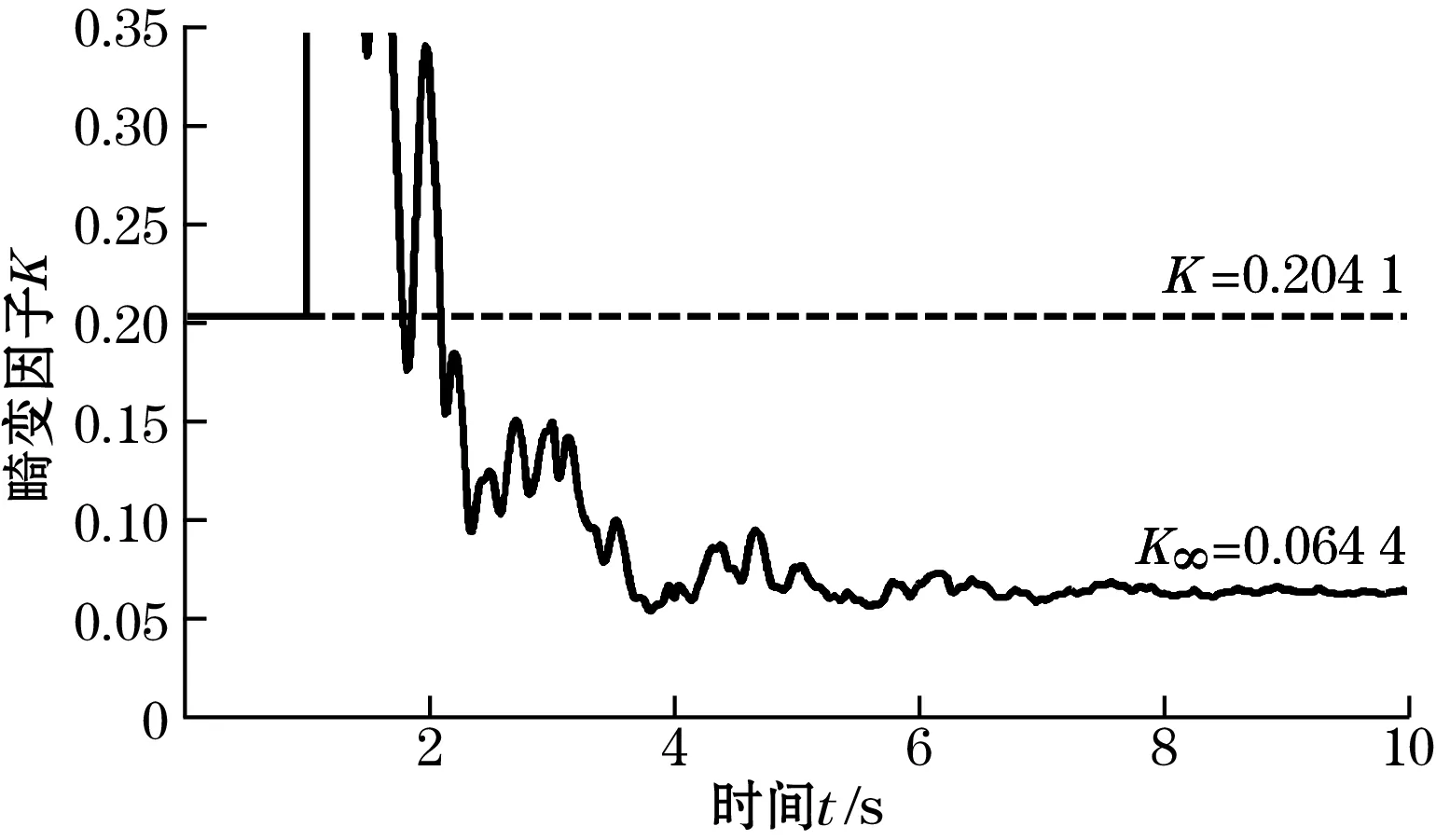
图14 激励磁场的畸变因子变化曲线图(励磁强度增大时)

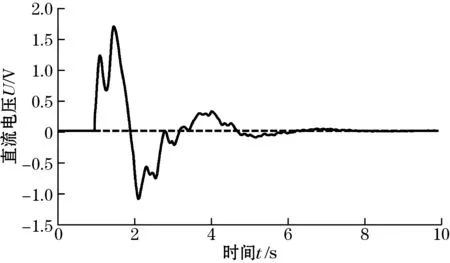
图15 激励磁场动态调节过程中的直流分量变化(励磁强度增大时)

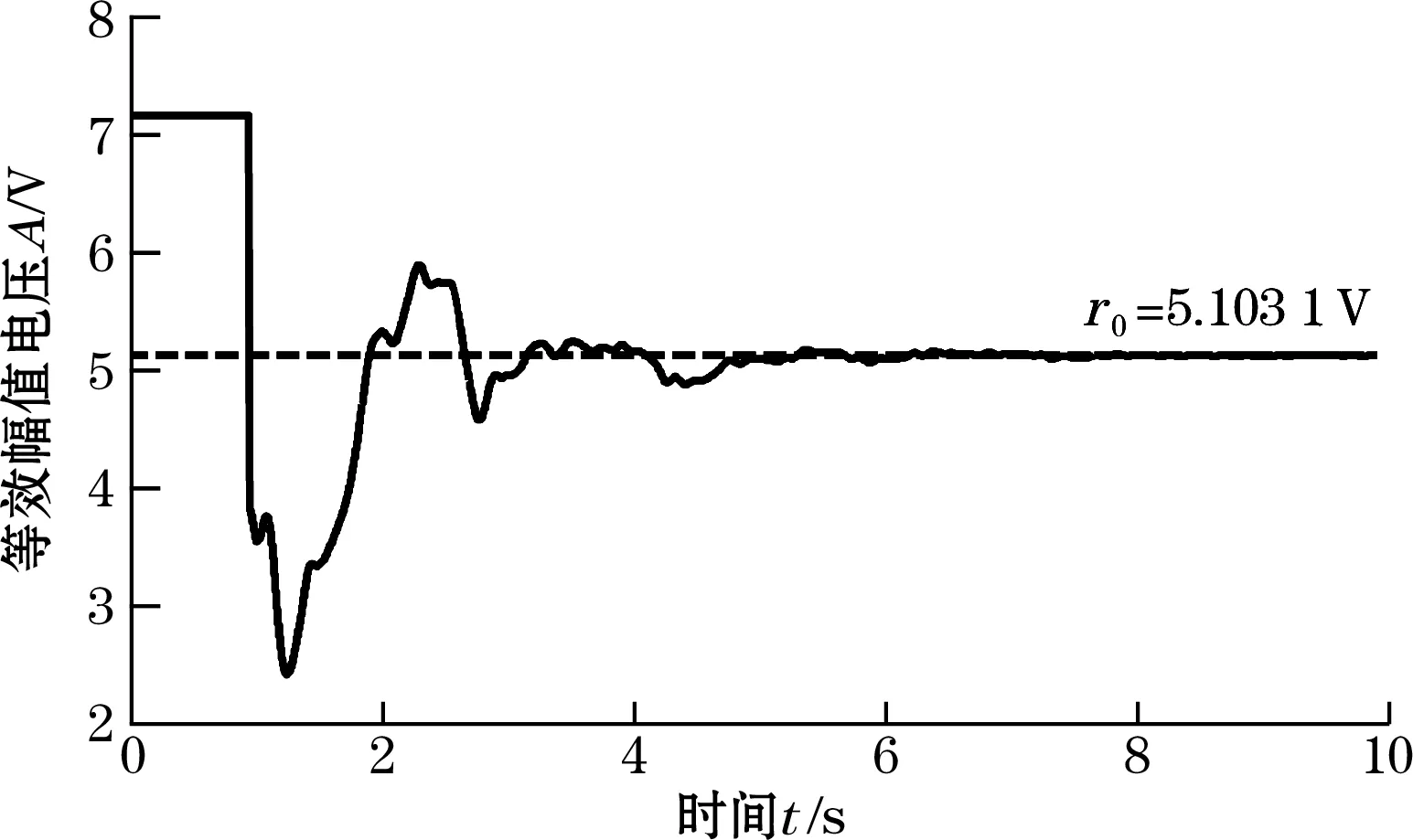
图16 激励磁场强度的变化曲线图(励磁强度增大时)

图17～图20为励磁强度减小为原来的0.6倍的强度稳定控制和波形畸变校正的仿真结果；结果显示大约经过6个周期的动态调节，直流分量消失，系统趋于稳定，波形畸变因子由初始的20.41%降到4.88%，同时励磁强度也实现了无静态误差的稳定控制。

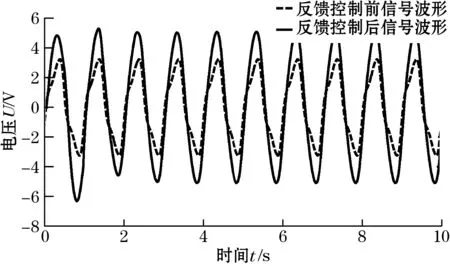
图17 激励磁场的波形对比图(励磁强度减小时)

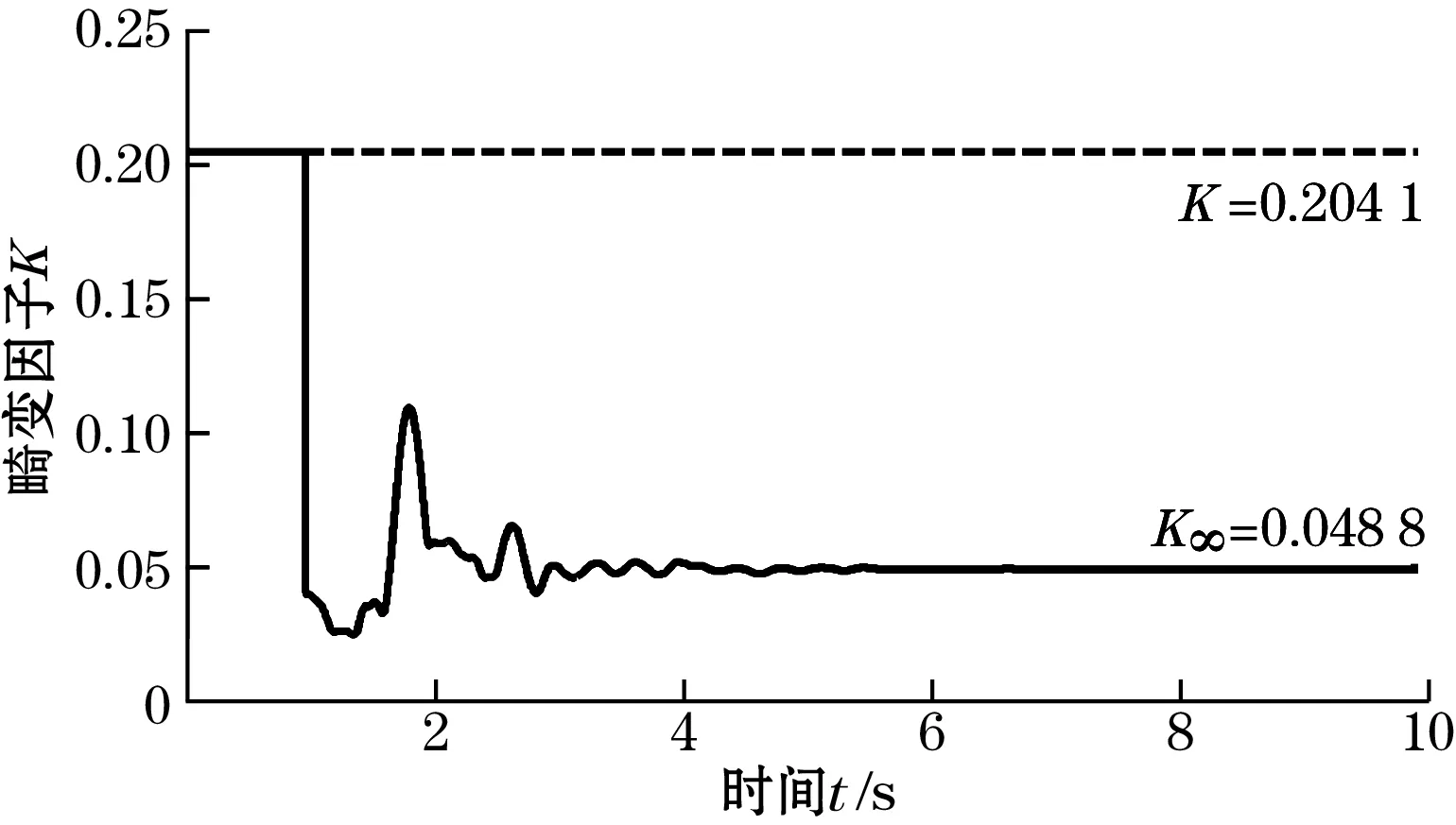
图18 激励磁场的畸变因子变化曲线图(励磁强度减小时)

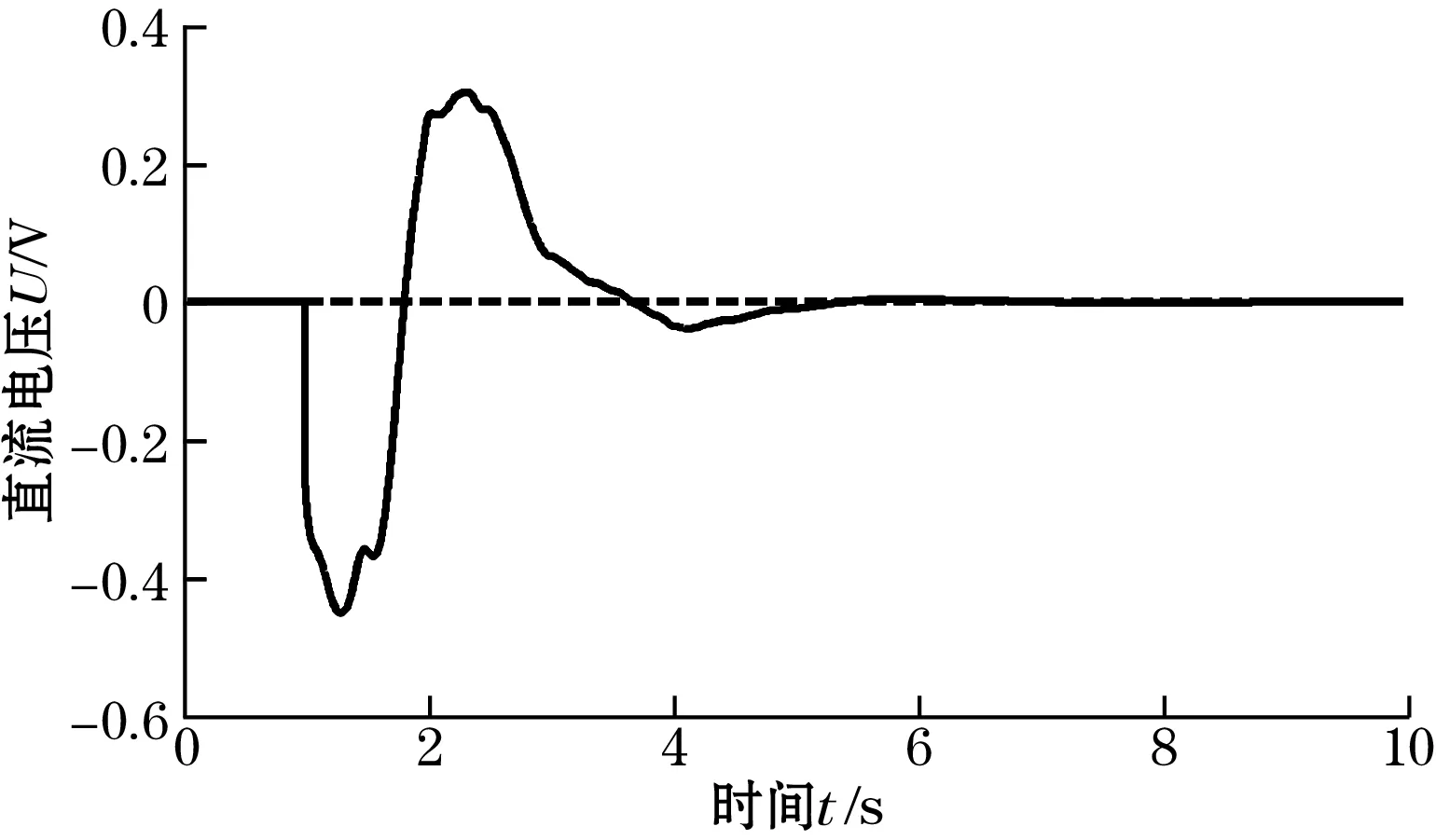
图19 激励磁场动态调节过程中的直流分量变化(励磁强度减小时)

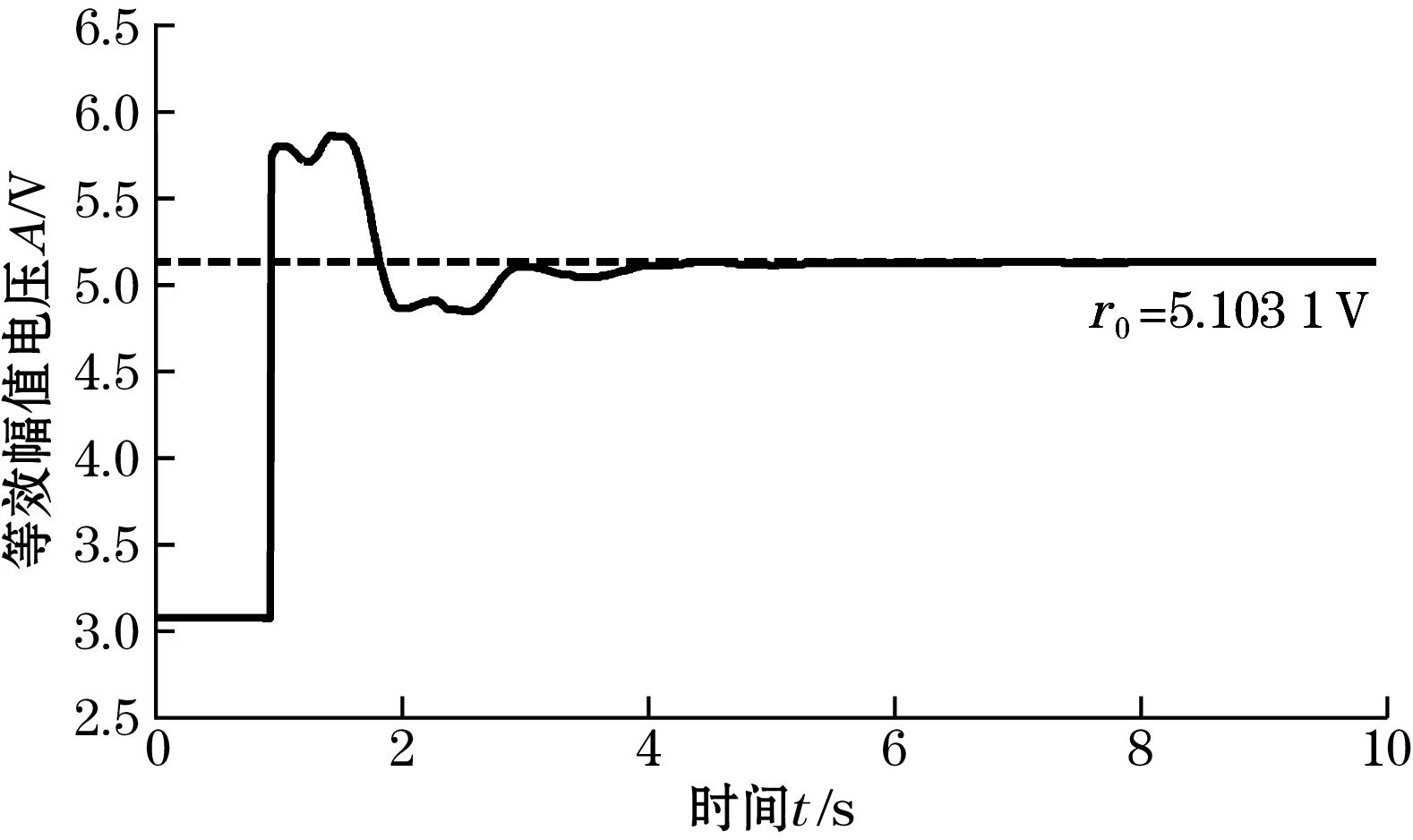
图20 激励磁场强度的变化曲线图(励磁强度减小时)

3 仿真结果分析与讨论

在闭环控制理论与模型中，假设MBN检测系统为一阶滞后系统，并且根据设定的系统输入和输出信号求出了系统的2个待定参数；对于实际中的MBN检测系统，则可以通过实际输入信号和霍尔元件(或置于试件表面的闭合线圈)的检测信号进行系统数学模型的辨识，从而确定系统的参数；而对于复杂的高阶系统，则可以不进行系统的数学模型辨识，可以直接针对实际的检测系统，通过典型的测试信号(比如单位阶跃信号)等，以硬件在环的方式在线进行PID参数的整定。对于计算机动态仿真实验的实施，本研究在系统输出端设定了3、5和7次谐波信号来模拟实际信号的畸变，对于实际的励磁信号畸变，则可以通过采集实际信号进行FFT分析确定畸变的各种谐波成分，从而有针对性地进行系统设计。

在系统设计与计算机动态仿真实验中，首先针对设定的初始励磁波形畸变(初始波形畸变因子为20.41%)进行了畸变校正，可以看出经过6个周期左右的动态调节时间，波形畸变因子降到5.28%。然后针对设定励磁强度增大为初始强度值的1.4倍和减小为初始值的0.6倍，进行了励磁强度的稳定控制，经过5个周期左右的动态调节，励磁强度稳定在初始强度值。最后，同时实施励磁波形畸变校正和励磁强度稳定控制，从仿真结果可看出双闭环PID负反馈控制系统可以有效对励磁波形畸变进行校正，对励磁强度可以稳定地控制在初始强度值。值得注意和深入考虑的是：应用PID控制器可以对励磁强度进行无静态误差的稳定控制，但是对于励磁波形畸变校正只是降低了波形畸变因子，并没有完全消除波形畸变，因此需要进一步研究其他的控制算法或畸变校正技术来彻底消除波形畸变。

4 结论

本文针对MBN检测的标准化实施要求以及为了实现不同MBN检测系统得到的检测结果可以进行直接对比的需求；在假设MBN检测系统为一阶滞后系统的基础上，通过设定系统输入和输出信号，设定励磁波形畸变和设定励磁强度的改变；基于MATLAB/Simulink软件进行PID负反馈控制系统设计并进行了计算机动态仿真实验，可以得到以下主要结论。

(1)应用PID控制器单独对激励磁场波形进行畸变校正，可以有效抑制高次谐波的产生，降低波形畸变因子，整个负反馈控制过程快速、平稳；仿真结果显示畸变因子由初始的20.41%降到了5.28%。

(2)应用PID控制器单独对激励磁场强度进行稳定控制，可以很好地对励磁强度进行稳定控制，整个负反馈控制过程快速、平稳并且无静态误差；仿真结果显示针对励磁强度增大和减小情况，均可实现系统的稳定控制。

(3)应用双闭环PID控制器同时实施励磁波形的畸变校正和励磁强度的稳定控制，可以有效降低波形畸变因子，可以很好地对励磁强度进行无静态误差的稳定控制，整个控制过程快速、平稳；系统的动态调节时间相比单独应用PID控制器对励磁波形进行畸变校正和单独应用PID控制器对励磁强度进行稳定控制的动态调节时间延长2～3个周期左右。