基于改进K-Means聚类算法的NBA球员价值评估*

蔡鹏飞,赵开新

(1.河南工学院 计算机科学与技术学院,河南 新乡 453003;2.河南省制造业物联网应用工程技术研究中心,河南 新乡 453003)

0 引言

球员价值的评估是困扰俱乐部管理者多年的一道难题。在信息膨胀的时代,数据来源不断丰富,数据规模迅速增加,数据让球队评估球员价值时可以更加严谨[1]。本文提出了一种改进的K-Means聚类算法,把NBA球员的数据集中起来进行分析,根据该算法的结果,可以实现对NBA球员价值的评估。

1 K-Means聚类算法

K-Means聚类算法是无监督的聚类算法,它实现起来比较简单,聚类效果也不错,因此应用得很广泛。K-Means算法的思想很简单:对于给定的样本集,按照样本之间的距离大小,将样本集划分为k个簇;让簇内的点尽量紧密地连在一起,而让簇间的距离尽量地大。

K-Means算法使用间隔作为相似性的评估参数,即意味着对象之间的间隔越近,其相似度越大[2]。K-Means算法认为类簇是由间隔接近的对象组合的,所以该算法把获得紧密和独立的簇作为终极任务。在实际使用K-Means算法的时候需要掌握k值的大小,即聚类数量,以达到最终的聚类效果。K-Means聚类算法的流程如图1所示。

图1 K-Means聚类算法的流程图

算法步骤为:

(1)在多个向量里任选出k个向量作为起始的聚类中心点。(2)以这k个中心点为参照点,计算出数据集中所有对象和这些中心点各自的间距。(3)数据集每个向量和k个向量的间隔不同,把向量和距离它最近的中心点划到一个类簇里。(4)重新计算每个类簇的中心点的位置。(5)重复第3步骤和第4步骤,直到类簇的聚类方案里的向量变化非常少时为止[3]。通常情况下,在完成迭代后,若是只有不到1%的向量还在聚类漂移,可认定为完成聚类。

K-Means算法的主要缺点有:k值的选取不好把握;对于不是凸的数据集比较难收敛;如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳;采用迭代方法,得到的结果只是局部最优;对噪音和异常点比较敏感。

2 改进的K-Means聚类算法

改进的K-Means聚类算法步骤为:

(1)在数据集里的所有点中随机选取一个点当成种子点。(2)逐个计算出数据集里的每个点和种子点之间的间距D(x)。(3)选择D(x)大的点作为新的种子点。(4)重复第2步骤和第3步骤直到新的种子被选出来。

对本算法而言,k的选取值相当重要,因为可在给出不同k值的时候,通过比较重要评价参数的变化程度,选取出相对合理的k值。当前主要的k值选取方法有拐点法和轮廓系数法。

拐点法比较简单,选取不一样的k值,并计算其簇内离差的平方和,绘制出线性图形,然后直观地从图中找出“拐点”以及其相对的k值。若簇的数量增加,则簇内样本的数量会变少,离差的平方和会变得更小[4]。

轮廓系数法的研究重点在于簇的密集和分散特性,把数据集划分成理想状态下的k个簇,则相应簇内的样本数会变密集,同时簇之间的样本数会分散。轮廓法的计算如公式(1)所示:

(1)

其中,a(i)表示簇内密集程度,样本i和相同簇内别的样本间距的平均值;b(i)表示簇间分散程度。计算方法为:样本i和别的非同簇的样本间距的平均值,之后从其中选取出最小的值。

本文分析拐点法和轮廓系数法的优点,在实际应用中采用两种方法综合选取最佳k值。

3 实验

3.1 实验环境、数据来源

本文的实验环境硬件为:CPU,Intel(R)Core(TM)i3-7100@3.90GHz;内存,8GB;操作系统,Windows10。软件编译环境为Python3.8。

实验数据为NBA球员投篮情况的记录,包含有球员姓名、隶属球队、每场得分和各种投球命中率等[5]。我们读入数据并观察其部分数据,部分数据实例展示如表1所示。

表1 NBA球员数据集的部分数据实例展示信息

在数据集中,具体参数,如得分、命中率、上场次数和时间等均是数值类型的变量,经观察发现一些数据间的量纲有所区别,因此要对数据执行标准化的处理流程。经研究本文选取得分、命中率、三分球命中率以及罚球命中率这4个维度作为球员集合聚类的指标参数[6]。

3.2 预处理

在Python编译环境中,球员数据标准化通过sklearn子模块的预处理中的scale函数和minmax_scale函数进行实现,scale函数和minmax_scale函数公式如(2)和(3)所示:

(2)

(3)

两个公式中mean(x)指的是变量x的平均数,std(x)为变量x的标准差,max(x)和min(x)分别为变量x的最大值与最小值。

3.3 数据可视化

实验过程如下:执行数据标准化算法初步绘制球员的得分和命中率之间关系散点如图2所示,并观察散点数据的分布,执行的算法如算法1所示。

算法1:数据标准化算法

(1)data←players,

(2)scatter_kws←{‘alpha’:0.8,‘color’:‘steelblue’}

(3)sns.lmplot(x=‘得分’,y=‘命中率’, data, fit_reg=False, scatter_kws)

图2 NBA球员得分和命中关系散点图

3.4 聚类中心选择

根据拐点法得出最佳k值,具体算法如算法2所示,并得到簇的个数图,如图3所示。

(1)X←preprocessing.minmax_scale(players[[‘得分’,‘罚球命中率’,‘命中率’,‘三分命中率’]])//数据标准化处理

(2)columns←[‘得分’,‘罚球命中率’,‘命中率’,‘三分命中率’]

(3)X←pd.DataFrame(X, columns)//将数组转换为数据框

(4)k_SSE(X,15)//使用拐点法选择最佳的k值

图3 用拐点法计算得到的簇的个数

随着簇数的增加,簇内离差平方和的总和在不断减小,当k值在4附近时,折线斜率变动变得缓慢,因此k值的选定范围是3或4。为了得到更精确的聚类结果,可以再通过轮廓系数法计算k值,对k值进行进一步的选择[7]。采用轮廓系数法得到的簇的个数图如图4所示。

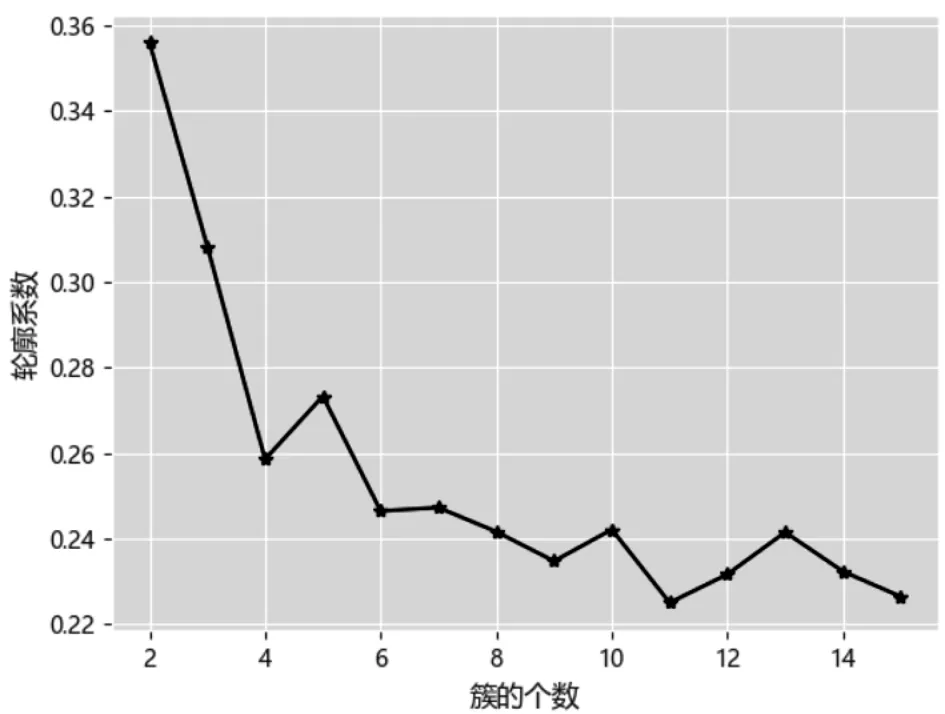
图4 用轮廓系数法计算得到的簇的个数

从图4可以看出,k值是2的时候对应的系数最大,k值是3的时候对应的系数次之,通过对两种方法得到的k值进行综合考虑,本文把最佳聚类k确定为3。

然后使用最佳k值对NBA球员数据执行聚类运算,具体实现如算法3所示。

(1)kmeans←KMeans(n-clusters=3)//定义聚类为3类

(2)kmeans.fit(X)//训练模型

执行上述代码得到聚类后的数据,再次画出得分和命中率关系散点图,通过散点图直观显示和分析聚类结果和效果,具体实现如算法4所示。

(1)players[‘cluster’]←kmeans.labels//定义聚类为3类

(2)for i in players.cluster.unique():

(3)centers.append(players.loc[players.cluster==i,[‘得分’,‘罚球命中率’,‘命中率’,‘三分命中率’]].mean())

(4)centers←np.array(centers)

(5)sns.lmplot(x=‘得分’,y=‘命中率’,hue=‘cluster’,data=players)

(6)markers←[‘＾’, ‘s’, ‘o’]

(7)fit_reg←False

(8)scatter_kws←{‘alpha’:0.8},legend=False)

(9)plt.scatter(centers[:,0],centers[:,2],c=‘k’,marker=‘*’,s=180)

(10)plt.xlabel(‘得分’)

(11)plt.ylabel(‘命中率’)

(12)plt.show()//图形显示

聚类后的散点图如图5所示。图中的三个五角星的意思是每个簇的中心点[8]。相对于正方形和圆形点来说,其差异表现为命中率的差异,正方形表示的球员的得分情况和命中率情况都相对比较低,说明这类球员的实力较差,命中率普遍在50%以下;圆形表示的球员则是代表了得分较低但命中率较高的类型,说明这一类球员很有可能为新球员,新球员的实力较强但由于上场时长少所以得数较低。而正方形和三角形点之间的区别表现在得分项上,三角形点代表得分较高而命中率较低的类型,说明这一类球员的上场时间和投球次数都多[9]。一个好球员的标准就是命中率和得分这两个数值都高,如图5里左上角的几个点表示的球员。需要注意的是,因本文在对数据集聚类前进行了数据标准化,所以聚类图的簇中心无法用cluater_centers_函数得到。

图5 聚类后的散点图

3.5 评估结果及分析

这三类球员的雷达示意图如图6所示,直观比较一下这三类球员在四个参数上的区别。因四个参数在量纲上有区别,无法保持一致,所以本文采用标准化后的簇中心画出雷达图,具体实现如算法5所示。

(1)centers_std←kmeans.cluster_centers

(2)radar_chart←pygal.Radar(fill=True)

(3)radar_chart.x_labels←[‘得分’,‘罚球命中率’,‘命中率’,‘三分命中率’]

(4)radar_chart.add(‘C1’,centers_std[0])

(5)radar_chart.add(‘C2’,centers_std[1])

(6)radar_chart.add(‘C3’,centers_std[2])

(7)radar_chart.render_to_file(‘radar_-chart.svg’)//保存图片

图6 三类球员雷达图

三类球员在每个维度都有差别,以C2和C3来说明,他们的平均得分并没有显著差异,但是C3的命中率却明显比C2高很多;再从平均的罚球命中率与三分命中率来看,C2普遍要比C3要强一些。

4 总结

本文提出了一种改进的K-Means聚类算法,在一个NBA球员数据集中进行聚类实现,通过观察聚类的结果,可以对比球员的特点,评估球员的价值,在实际应用中可以辅助球队挑选人才。与传统方法相比,该聚类方法功能更丰富,应用更灵活。这个算法对于异常的点较敏感,其中心点是通过样本均值确定的。假如聚类数的量纲不同,就需要进行数据的标准化。如果数据中含有离散型的字符变量,就需要对该变量做预处理,如设置为哑变量或转换成数值化的因子。下一步工作主要研究对未知聚类个数的数据集采用探索方法以寻找最佳k值。