电动汽车锂离子动力电池建模及温度场分析*
2021-09-27于建新王红霞
常 成,于建新,王红霞,金 毅
(1.河南工学院 车辆与交通工程学院,河南 新乡 453003;2. 一汽-大众汽车有限公司,吉林 长春 130011)
0 引言
动力电池是纯电动汽车及混合动力汽车的储能装置,其性能是决定汽车品质的主要因素之一。锂离子动力电池具有高能量密度、高功率密度、自放电功率低、无记忆效应、循环寿命长等特点,目前已成为电动汽车动力电池的主要类型[1]。锂离子动力电池在充放电过程中会出现温度升高现象,当温度超过临界温度时,电池将发生热失控,造成电池和连接电路的损坏,同时也会引发各种安全问题[2],因此,充分了解动力电池在散热时的温度场分布是十分必要的。但单体电池都密封在电池壳体内,通过在单体电池内安装传感器进行温度测量显然难以实施。目前许多相关文献都是通过建立有限元等效模型,利用计算机仿真来得到动力电池的温度场分布。文献[3]建立了锂离子聚合物方形电池的二维简化模型,并通过红外热成像仪验证了模型的有效性;文献[4]根据方形动力电池结构特点,建立了热参数等效数学模型和动力电池三维不分层有限元模型;文献[5]在单体电池热参数的基础上,建立了电池组数学热模型,并通过有限元软件模拟了电池组的热特性;文献[6]根据内阻和电化学反应来确定电池热源,建立圆柱形锂离子电池在1C放电条件下的三维有限元热模型,得到不同放电时间的温度场分布。由于单体电池内部结构复杂且由多种材料组成,而且其内部各种材料的热参数并不相同,建立详细的模型较为困难。因此,需要对模型进行适当简化来建立便于计算的等效模型。
为了提高等效仿真模型的准确性,本文依据18650锂离子动力电池的结构特点,提出等效参数求解方法,并基于Ansys-workbench仿真平台中的Fluent模块,建立单体电池有限元等效模型,以此为基础来研究单体电池和电池组的热特性,以期为电动汽车动力电源的发展提供参考。
1 单体电池结构及生热机理
18650锂离子电池主要包括三部分:(1)正极、负极、隔膜和电解液所组成的芯体;(2)正负极接线柱、绝缘板、PTC元件、保护阀和垫片等附属结构;(3)电池金属外壳。其结构如图1所示[7]。
电池芯体是由正极片、负极片和夹在其间的隔膜共同卷绕而成,其中正极片是在正极集流体双面涂覆正极活性物质层而形成的,负极片是在负极集流体双面涂覆负极活性物质层[8]而形成的。电池芯体结构如图2所示。
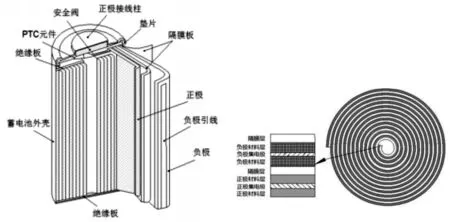
图1 18650锂电池结构示意图 图2 卷绕式锂离子电池芯体横截面示意图
根据锂离子电池工作原理可知,在充放电工作过程中,锂离子通过电解液透过隔膜在两极间迁移,并不断产生复杂的化学反应,与此同时会伴随着热量的产生,因此单体电池的发热源主要集中在电池芯体。
在电动汽车行驶过程中,由于路况和交通状况的随机变化,动力电池工作电流的变化是没有规律的,因此,这是一个时变内热源的非稳态导热过程。电池内部的温度变化可用下述非稳态传热的能量守恒方程来描述[9]:

(1)
其中,ρk表示电池微元体密度,Cp,k表示电池微元体比热容,λk表示电池微元体导热系数,q表示内热源生热速率。
研究热模型时需要计算电池内部的热生成率,锂离子电池的生热源主要来自四个方面:反应热、极化热、焦耳热以及副反应热[10]。单体电池体积狭小,内部结构复杂,很难通过测量来获得电池内部的发热功率。为了解决这一难题,目前公认有效的生热功率模型之一是Bernadi电池生热功率模型[11]。
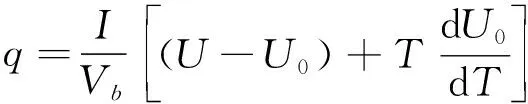
(2)
式中,U表示端电压,单位为V;I表示电流强度,单位为A;U0表示开路电压,单位为V;Vb表示电池体积,单位为m3。
本文将采用Bernadi电池发热功率模型公式来计算电池放电过程中的产热功率。由于电池内部电解液流动十分缓慢,热对流的温度传递影响很小,此外热辐射的影响也极小,因此本文只考虑热传导对电池的换热作用,其大小与电池内各材料的导热系数有关。
2 芯体热阻模型建立及参数确定
2.1 芯体热阻模型
依据传热学理论,对于单层平壁导热过程,其热阻Rp可表示为[12]:
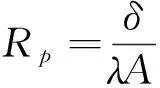
(3)
其中:δ为平壁厚度,λ为导热系数,A为平壁表面积。
对于单层圆筒壁导热过程,其热阻RT可表示为:
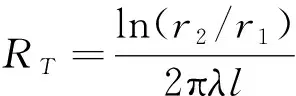
(4)
其中,r1和r2为单层圆筒壁内外半径,l为单层圆筒壁高度。
由电池单体的结构可知,芯体是由多层不同材料卷绕而成,电池的导热系数为各向异性。芯体各层元件的厚度相对芯体整体尺寸较小,可近似认为正、负极片和夹在其间的隔膜为一个单元,并呈同心的环形布置,以此可建立电池芯体热阻模型。
设电池芯体是由两极片和其间的隔膜卷绕N圈制成,则同心环简化模型就是由N组紧密贴合的同心环组成,每组同心环由8层材料构成,且各组环中的材料层排列顺序相同。在忽略接触热阻的前提下,轴向的等效热阻模型Ra可表示为:
(5)
其中,λn为第n层材料的导热系数,rn为第n层材料层的内半径,rn+1为第n层材料层的外半径。
依据电池芯体的结构特点,正、负极材料的层状结构和隔膜中的孔隙都含有电解液。若隔膜中的电解液占隔膜体积的比例为ks,可认为隔膜材料所占隔膜体积的比例就为1-ks。隔膜层在电池轴向可视为是电解液和隔膜材料串联而成,可得到隔膜层轴向等效导热系数λsla:
(6)
同理,正、负极材料层的轴向等效导热系数λpla和λnla为:
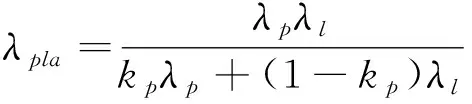
(7)
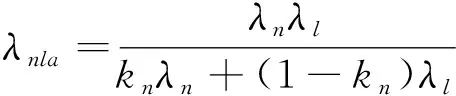
(8)
其中,λs为隔膜材料导热系数,λl为电解液导热系数,λp为正极材料导热系数,λn为负极材料导热系数,kp为电解液占正极材料层体积的比例,kn为电解液占负极材料层体积的比例。
在电池芯体径向的方向上,热量是通过多层圆筒壁进行传导的,可得芯体径向方向热阻模型Rr:
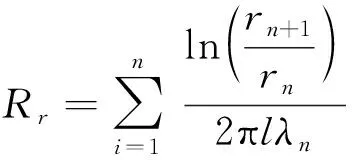
(9)
隔膜层在电池径向可视为电解液和隔膜材料并联组合,则隔膜层径向等效导热系数λslr为:
λslr=ksλl+(1-ks)λs
(10)
同理,正极材料层径向等效导热系数λplr和负极材料层径向等效导热系数λnlr为:
λplr=kpλl+(1-kp)λp
(11)
λnlr=knλl+(1-kn)λn
(12)
2.2 电池芯体热参数的确定
为方便建立仿真模型,可将多层材料构成的电池芯体简化为单一材料实体模型。为分析电池芯体的温度场分布,需确定该简化实体材料的密度、比热容和导热系数。
2.2.1 芯体平均比热容
比热容ca通常通过对组成材料的热容量加权平均的方法进行计算[13],计算公式如下:
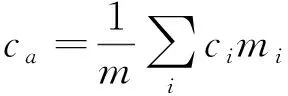
(13)
式中,m是单体芯体的质量,ci是某种材料的比热容,mi是相应材料的质量。
2.2.2 芯体平均导热系数
利用前文中电池芯体各向等效热阻,可推导出电池芯体相应方向的平均导热系数。
电池芯体轴向的平均导热系数λa为:
(14)
其中,rmax为电池芯体外半径,rmin为电池芯体内半径。
电池芯体径向的平均导热系数λr为:
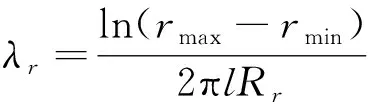
(15)
3 单体电池热仿真
3.1 单体电池模型建立
本文采用某18650电池为研究对象,锂离子电池基本参数见表1所示。

表1 18650锂离子电池基本参数
由于单体电池包含的部件体积尺寸较小,全部构建起来十分复杂,同时考虑到以电池组为研究目标时,电池构件的细节对整个电池组的热仿真没有太大影响,本文将单体电池结构做适当的简化。简化后的模型由芯体、附件体和壳体三部分单一材料实体构成,见图3所示。

图3 单体电池简化结构
热参数计算所涉及电池各组成结构的材料属性,见表2所示。这三部分实体中,芯体作为产热区域,可依据公式(2)得到不同的放电电流相应的产热功率。由于电池单体沿径向对称,可取1/2电池模型作为计算对象,经过网格剖分后,其节点数为137,638、单元数为26,239。
表2 电池材料参数
3.2 仿真结果及分析
电动汽车在加速、爬坡等过程中,电池的放电倍率会在较短的时间内发生很大的变化[14]。因此,研究不同放电倍率时电池的热效应是十分必要的。考虑到实际使用中电流值的范围,对单体模型进行0.5C、1C和2C放电倍率的温度场分布模拟。仿真条件中初始温度和环境温度均设为25℃,以自然对流的方式对外界散热,放电时间为420s,放电结束时刻的温度场分布如图4所示。从图中可知,单体电池在以不同倍率放电时,电池温度分布规律大致相同,由于电池芯体所处位置靠近负极端,电池的最高温度分布在中心稍微偏下的区域,由电池中心向电池外表面呈逐渐降低的温度梯度分布,电池负极端的表面温度要高于正极端。随着放电倍率的增加导致电池整体温度升高,内外温差也逐步加大,当放电倍率为2C时,电池最高温度已达到42.3℃,最高温度与最低温度的差值达到3.8℃。但由于电池表面金属材料导热性能较强,电池表面的温差并不大。

a)0.5C b)0.5C c)2C图4 不同放电电流时单体电池温度分布云图
3.3 单体电池放热试验验证
为验证单体电池有限元模型的有效性,在试验所处条件与仿真边界条件相同的情况下,对单体电池进行放热试验。本试验选用安捷伦N7909A功耗单元和N7954A先进电源系统作为电池的放电设备;选用横河公司的MV2000便携式无纸记录仪,通过连接热电偶传感器,直接将检测到的表面温度实时记录。在电池圆柱面的轴向中点和距离该点上下各15mm处布置3个热电偶,从正极端到负极端依次是测试点①、②、③。图5为试验原理示意图,图6为试验设备实物连接图。

图5 试验原理示意图 图6 试验设备实物连接图
在环境温度为25℃时,对电池分别进行放电倍率为0.5C、1C和2C且放电时间均为420秒的温度数据采集。各测试点温度随时间变化曲线如图7所示。
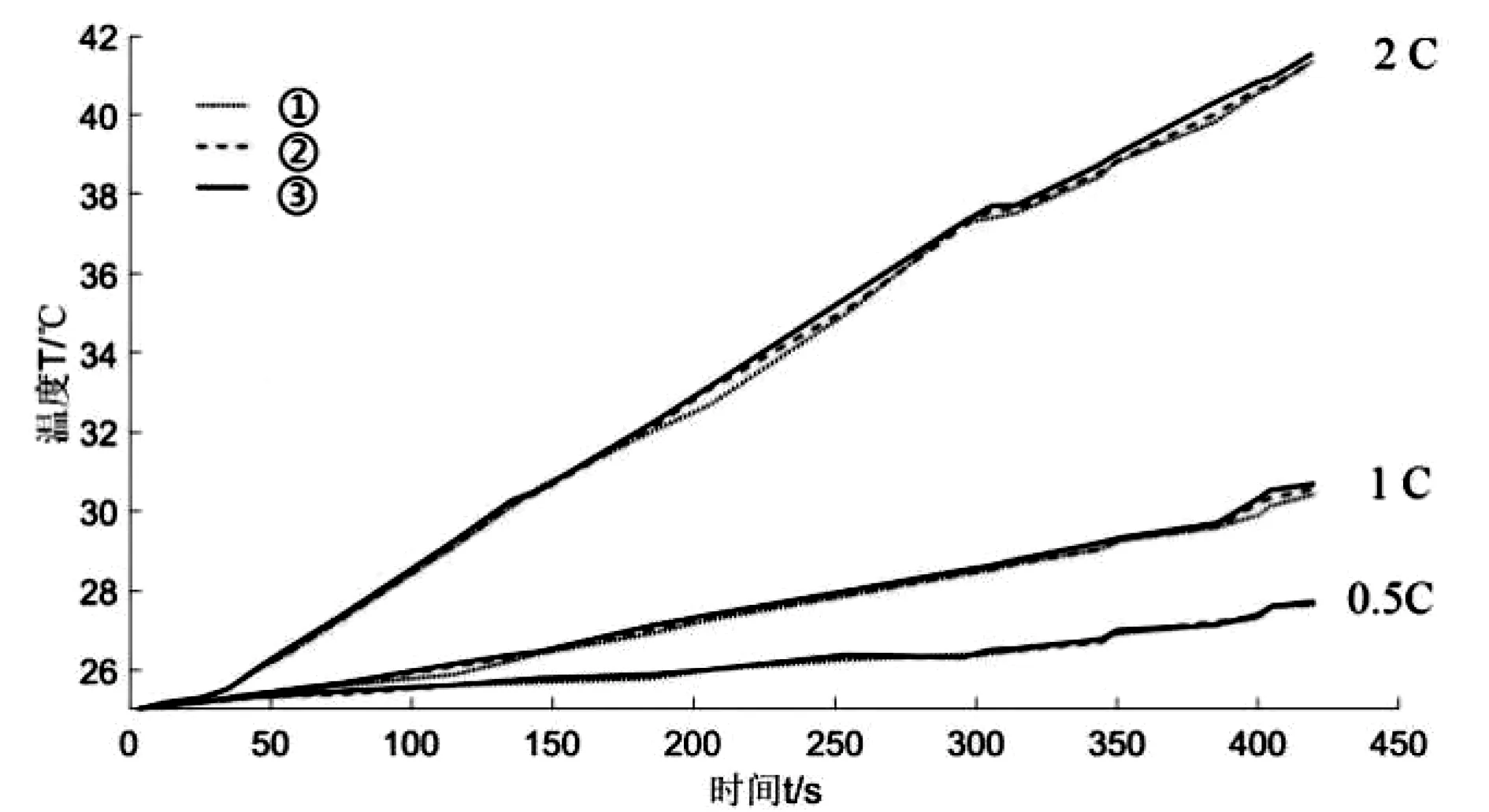
图7 不同放电电流时各测试点温度变化
通过观察可以得出,电池表面温度随时间的增加而趋于线性增长,放电电流越大,温度曲线的斜率越大,温度增长得越快。相同放电电流对应三个测试点的温度值存在一定差异,与仿真结果得到的结论相同,靠近电池负极端的表面温度高于正极端,且在相同的放电时间里,放电电流越大,温度差异越大。当放电时间均为180秒时,放电电流为2C时的表面最大温差为0.7℃,0.5C时的表面最大温差仅为0.1℃,两者相差0.6℃。在1C放电过程中,120秒时表面最大温差为0.1℃,随着时间的增长,到360秒时表面最大温差已达到0.4℃。
现将电池表面测量值与其仿真值相对比,见图8所示。
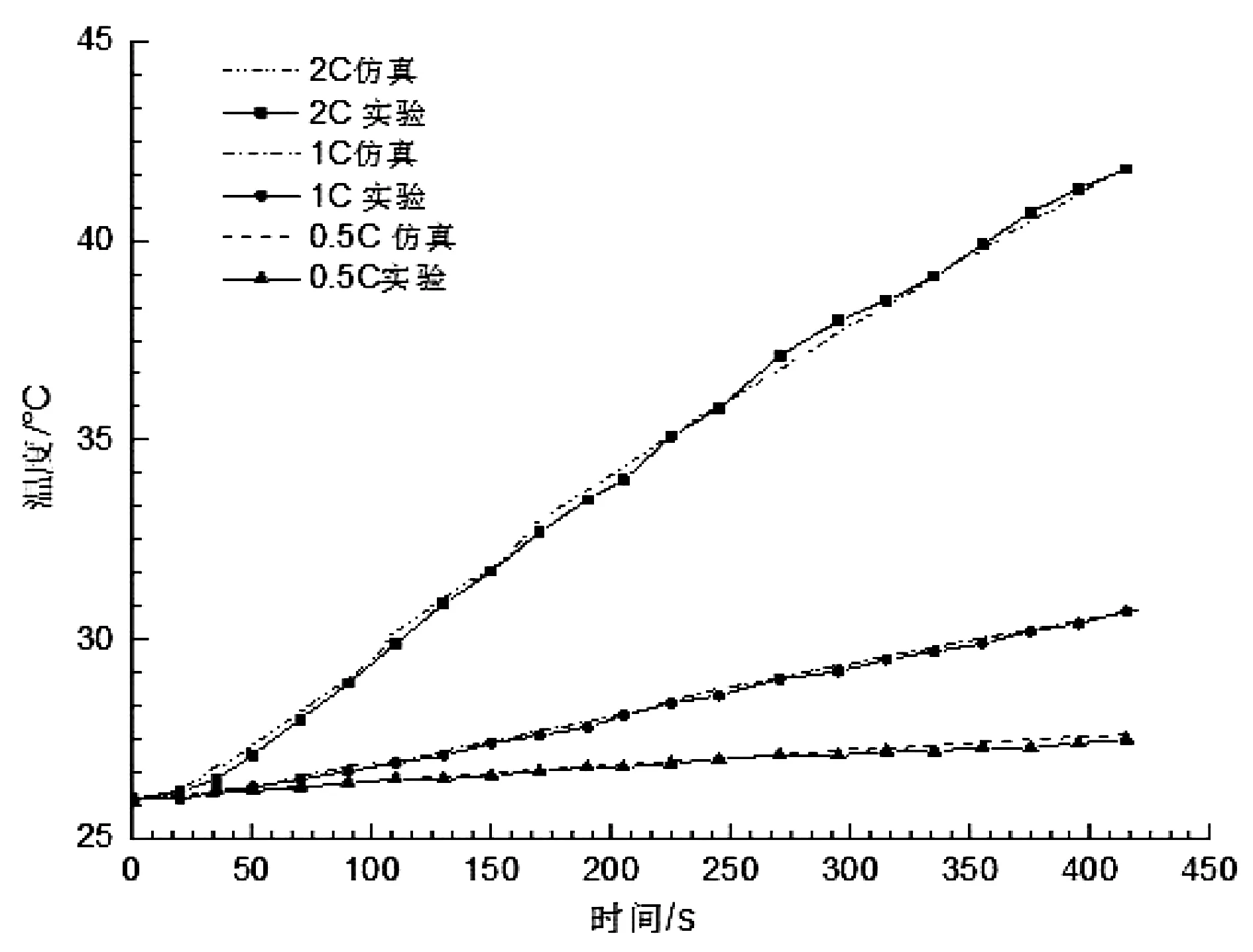
图8 仿真与试验中电池表面温度对比曲线
可以看出两条温度变化曲线的趋势及数值均相差较小,最大差值仅为0.3℃,从而可以说明本文所建立的单体有限元模型是有效的。
对比仿真结果可知,电池内部温度分布不均匀,仅凭温度传感器所测得的表面温度,是难以得知电池内部最高温度的,而通过有限元仿真模型,可以进一步研究电池内部的热特性,这样才能合理控制电池温度,有效防止热失控的出现。
4 电池组温度场分析
4.1 电池组换热系统建模
动力电池是电动汽车的能量来源,需将电池单体通过串并联组成电池组,为电动汽车提供足够的电压、电流以及足够高的能量存储能力。由于汽车空间有限,导致单体电池间排列致密,使散热难度加大。电池组的温度分布不仅与单体电池本身有关,同时还受到周围传热介质的影响[15]。
在上述所建单体电池模型的基础上,建立电池组三维仿真模型。该电池组包含96节电池单体,首先将每12节串联成8组,然后将这8组并联,并将该电池组安装于带有换热介质出入口的电池箱内。本文利用变压器油的绝缘和比热容大的特性,采用变压器油与电池表面直接接触换热的方案,以此来增强换热介质对电池的换热效果。变压器油参数如表3所示。

表3 变压器油热参数
为研究换热介质出入口位置对电池组温度的影响,本文提出三种换热端口位置不同的结构方案,分别是端口在同侧布置的电池组A、端口在电池箱几何轴线上布置的电池组B和端口呈对角线布置的电池组C,三种结构如图9所示。
设置入口质量流量为0.03kg/s,入口换热介质温度为25℃,系统整体的初始温度均为25℃,仿真换热时间为300秒,分别将以上三种方案添加到Fluent模块中进行温度场仿真计算。经仿真计算,不同散热装置中的电池组极限温度随放电电流的变化如图12所示,其中,Tmax表示电池组最高温度值,Tmin表示电池组最低温度,ΔT表示电池组的极限温差。为研究这三种结构对电池组温度的影响,本文将忽略电气连接线和电池箱体与外界的传热影响。
4.2 结果分析
由仿真得到的极限温度值可知,三种系统均能在很大程度上改善电池组的温度。由于电池单体数目较多,冷却介质不能对所有的电池单体同时进行散热,冷却介质在流动的过程中,不断吸收电池传递出来的热量,温度会有所上升,从而导致介质出口附近的电池温度略高于介质入口附近的温度。另外,若出入口相对位置不同,则介质在电池壳体内的流通路径也不同,从而使得上述三种系统中的电池温差也存在差异。
从图10中可以看出:电池组A和电池组B的极限温度值偏高,且极限温差较大;电池组C的极限温度值最低,且极限温差最小。当放电电流为41.6A时,电池组C最高温度为33.3℃,较电池组A和电池组B分别低1.8%和4.2%;而电池组C此时的极限温差为4.9℃,较电池组A和电池组B分别低4.1%和24.5%。随着放电电流增大,极限温度和极限温差都增加,电池组B的增长幅度最大,电池组C的增长幅度最小。
从结构上分析,电池组A在远离介质端口一侧的流阻大,影响了远离端口一侧的电池单体与换热介质间的对流换热强度,造成了热量累积。电池组B的介质出入口位于中间,对四周空间的扩散性不足,造成电池组四个角落位置流动性较差,导致温度相对较高。相比而言,电池组C的散热结构较为合理,温度均匀性较好。

(a)电池组A (b)电池组B (c)电池组C图9 出入口位置不同的换热结构图
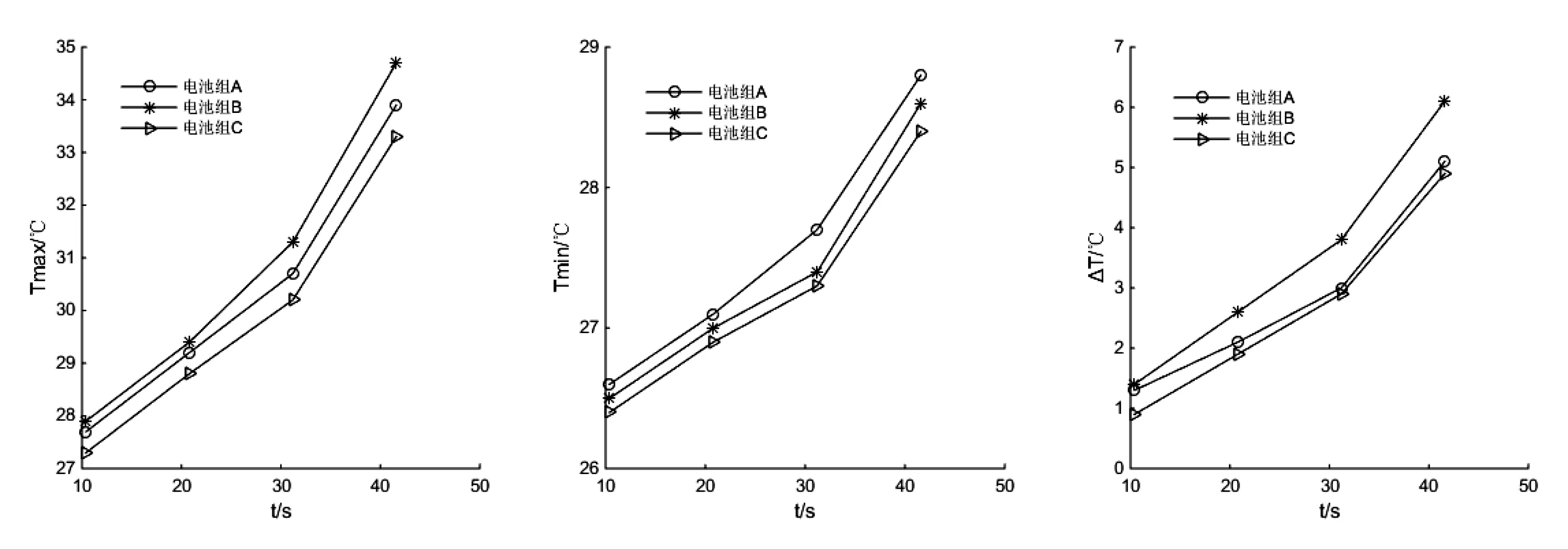
图10 300秒时不同散热装置温度对比曲线
5 结语
(1)通过分析18650动力电池的结构,建立了电池芯体的简化模型,并考虑到电解液对隔膜层和电极材料层的传热影响,得到了各向平均导热系数的值。
(2)建立了电池单体有限元等效模型,进行了不同放电电流对应的温度场计算。结果表明,电池内外存在较大温差,且电池负极端温度略高于正极端温度。将仿真计算结果与试验结果相对比,验证了所建模型的准确性。
(3)利用所建电池单体有限元模型,建立了电池组有限元模型,在此基础上提出了三种冷却结构,并进行了温度场分析。结果表明,介质端口呈对角线布置的冷却结构具有良好的散热效果。
