航空重力测量中垂直加速度改正的固定区间平滑算法研究*
2021-09-27陈学锋闫雷兵
郑 崴,魏 辉,陈学锋,闫雷兵
(1.河南工学院 电子信息工程学院,河南 新乡 453003;2.新乡市信号与信息处理重点实验室,河南 新乡 453003)
0 引言
航空重力测量是在飞行状态下,利用航空重力测量系统进行重力测量的新型动态测量技术。测量过程中,航空重力仪会受到飞机发动机的振动、飞机垂向运动、气流颠簸及飞机高度变化等造成的扰动加速度的干扰[1,2]。这些扰动加速度中又以飞机垂向运动对航空重力仪的干扰最大,其量级可达到104毫伽以上,远大于百十毫伽重力异常信号[3,4]。并且,该扰动加速度具有一定的随机性,无法采用严密的解析公式进行补偿修正,因此,在航空重力测量数据处理阶段,须采用滤波、平滑等多种信号处理技术来补偿这部分扰动加速度干扰,这个过程即为航空重力数据处理的垂直加速度改正。目前,基于傅里叶变换的频域数字滤波和基于系统模型的卡尔曼滤波是实现垂直加速度改正处理的主要方法[5-7]。我国研制的三轴稳定平台式航空重力测量系统的数据处理软件即采用了卡尔曼滤波进行垂直加速度改正处理[8]。卡尔曼滤波是在时域内依据最优估计理论实现全频带干扰的修正,依据状态估计时刻所用到的量测信息情况,最优估计可以分为预测、滤波和平滑三类。其中,滤波是利用当前时刻以及此前时刻的所有量测信息对当前状态进行估计的算法。而平滑除了利用滤波所用的量测信息外还利用了当前时刻以后的部分或所有时刻的量测信息[9]。因此,平滑是一种离线处理算法,能够获得优于滤波的估计精度。常用的平滑算法主要有固定点平滑、固定滞后平滑和固定区间平滑。
结合航空重力测量垂直加速度改正事后处理的特点,平滑算法的应用可以提高垂直加速度改正的精度。国内外众多学者开展了卡尔曼滤波在航空重力测量中的应用研究。蔡体菁等人构造了扩展卡尔曼滤波方程进行重力异常信号提取的方法[10];俄罗斯国立大学的Bolotin等人在惯性导航误差补偿模型的基础上将待估计重力异常信号作为状态向量构建航空重力异常估计的模型,并通过实测数据验证了构建模型的有效性[11];张贵宾等构建了基于重力异常模型的信息提取方法,并设计固定区间平滑器提高了重力异常估计精度[12,13]。尽管上述研究取得了一定的进展,但这些研究仍主要聚焦于滤波算法以及模型的构建上,对于平滑算法研究较少。在具体的平滑算法、设计及处理方案等方面,对航空重力测量垂直加速度改正的平滑处理来说,还需进一步研究分析不同平滑算法在数据处理中的特性,从理论和应用两方面进行综合考虑,选取合适的平滑算法。
本文针对航空重力测量数据处理中的垂直加速度改正处理,在经典卡尔曼滤波算法的基础上,结合工程实际条件,对两种固定区间平滑算法——TFS(Tow-Filter-Smoothing)算法和RTS(Rung-Tung-Striebel)算法在重力异常提取中的应用进行仿真试验,分析两种算法在航空重力测量数据处理中的特点和适用方案。
1 固定区间平滑算法原理
固定区间平滑是利用时间间隔内所有量测值来估计系统在这个时间内整个过程的状态的算法[14]。TFS算法和RTS算法是两种常用的固定区间平滑算法,其中TFS算法是先进行时间顺序的卡尔曼滤波(前向滤波),然后再按照时间的逆序自后向前再次进行滤波(后向滤波),最后对两次滤波结果进行数据融合实现平滑;RTS算法同样也是先进行时间顺序的卡尔曼滤波,但其后向滤波是在前向滤波的基础上进行修正完成数据融合的。两种平滑算法的流程图如图1所示。

(a)TFS算法流程

(b)RTS算法流程图1 固定区间平滑算法流程图
1.1 TFS算法
不难发现,TFS算法实际上包含了两个独立的滤波过程——时间顺序的前向滤波和时间逆序的后向滤波,之后再将两个滤波结果进行数据融合,而数据融合则是以两个滤波过程中估计的协方差为依据进行加权平均。其具体处理过程为:
第一部分,前向滤波。前向滤波本质上就是标准卡尔曼滤波,对于一个线性离散系统,其系统方程和量测方程可分别表示为
Xk=Φk,k-1Xk-1+Wk
(1)
Zk=HkXk+Vk
(2)
式中,Wk~N(0,Qk),Vk~N(0,Rk),则前向滤波按照k=1,2,…,N的顺序依据卡尔曼滤波基本方程确定每个时刻的状态估计[14]:
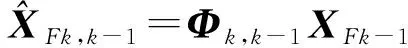
(3)

(4)

(5)
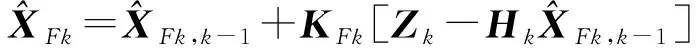
(6)
PFk=[I-KFkHk]PFk,k-1
(7)

第二部分,后向滤波。由于要保证前向和后向滤波的独立性,后向滤波通常采用信息滤波算法按照k=N,N-1,…,1逆序进行状态估计,有[14]

(8)

(9)

(10)
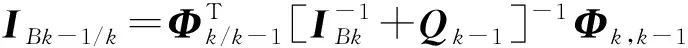
(11)

(12)
式中,IBk,IBk-1/k分别为后向估计协方差的逆和后向预测协方差的逆,即
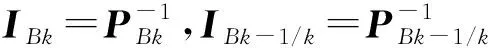
(13)

Psk=(IFk+IBk)-1
(14)

(15)

1.2 RTS算法
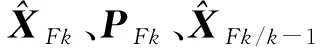

(16)
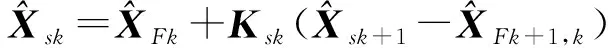
(17)

(18)
可以看到,RTS算法是在后向处理过程中实现数据融合完成平滑的,相较于TFS平滑算法,其在后向滤波过程中同时实现数据融合。
2 数据仿真试验
2.1 试验设计
设待测区域有一半径为400m、顶部埋深为100m的规则球体,且球体的剩余密度为0.15 g/cm3。现有测量间隔为4m、长度为4000m的航空重力测量测线位于球体上空,球心位于测线2000m处,则可得重力异常理论值如图2所示。
测量过程中,航空重力仪受到飞机随机垂直运动产生的扰动加速度干扰,为获得满足精度要求的重力异常信息,需对测量结果进行滤波平滑处理。设垂直扰动加速度是均值为零、方差为20 mGal2的白噪声,如图3所示。不难看出,重力异常已经完全被噪声淹没且噪声的强度比所需信号高出一个数量级。

图2 球体模型重力异常

图3 重力异常与扰动噪声干扰
2.2 平滑试验与分析
现分别采用TFS平滑算法与RTS平滑算法对重力仪观测结果进行滤波平滑处理。由于两种平滑算法都基于卡尔曼滤波,因此需要建立系统方程和量测方程。设重力异常在采样间隔的变化为ux,取其一次近似,有[13]

(19)
式中,x为测线位置,M为剩余质量,D为球体模型埋深。采样点处的重力异常为gx,采样间隔为Δx,则可得系统方程
gx=gx-1+Δxux-1+qx-1
(20)
式中,qx-1是系统噪声项,它是均值为零、方差为Qx-1的高斯白噪声。同时,以重力仪的观测方程作为量测方程,有

(21)
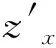
2.2.1 TFS平滑试验
在构建的系统方程和量测方程的基础上,采用TFS算法进行平滑处理,前向滤波过程按照式(3)-(7)标准卡尔曼滤波方程进行处理并存储所需的状态估计和估计协方差,后向滤波按照式(8)-(13)进行处理并存储后向滤波的状态估计和估计协方差,之后再按照式(14)、(15)进行数据融合实现TFS平滑处理。平滑结果如图4所示。
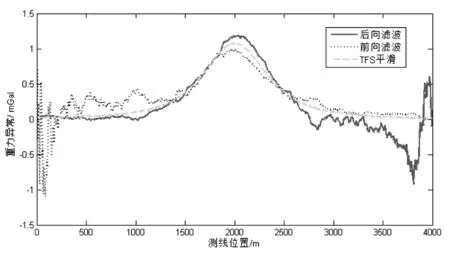
图4 前向滤波、后向滤波和TFS平滑对比
由图4可知,前向滤波结果由前向后逐渐收敛,而后向滤波结果由后向前逐渐收敛,但两者相较于理论重力异常曲线都有较大的差别。而将前向滤波和后向滤波结果进行融合后所获得的TFS平滑结果比较规则,也更接近于理论值。这说明,进行数据融合后所实现的平滑优于两次滤波的结果。
2.2.2 RTS平滑试验
采用RTS算法进行平滑处理中,前向滤波同样按时间顺序依据卡尔曼滤波方程处理,并依次记录所需的状态预测、预测协方差、状态估计及估计协方差。再按照式(16)—(18)实现平滑处理,平滑结果如图5所示。不难看出,RTS算法同样可以消除在滤波初始阶段由于滤波器未收敛带来的估计误差,也使得经过垂直加速度改正后的重力异常曲线更加平滑。

图5 前向滤波和RTS平滑对比
2.2.3 TFS平滑与RTS平滑对比
将TFS算法平滑结果、RTS算法平滑结果分别同重力异常理论值进行对比,结果如图6所示。不难看出,经过TFS算法和RTS算法平滑处理后,都可以获得与理论值形状一致的重力异常结果,附加在测量结果的噪声被压制,平滑后的重力异常曲线形状与理论值基本一致。
分别统计TFS算法与RTS算法平滑处理的误差,结果如表1所示。TFS算法与RTS算法都可以较好地压制扰动噪声,两者性能基本相当,TFS算法获得重力异常均方误差为0.006 mGal,RTS算法均方误差为0.005 mGal,二者在精确度上略有差别。同时也应注意到,TFS算法平滑处理的数据融合阶段需要一直求解系统模型的逆矩阵,因此存在计算量大、逆向模型不易求解的问题。

图6 TFS平滑与RTS平滑对比

表1 TFS平滑与RTS平滑处理重力异常误差对比
3 结论
本文对固定区间平滑算法的基本原理进行了研究分析,并着重研究了TFS算法和RTS算法的原理,在此基础上,将它们应用于航空重力测量的模型试验,并分析了两种平滑算法的性能。
由试验结果可知,在航空重力测量垂直加速度改正处理中,由于TFS算法和RTS算法都采用了更多的量测信息,可以获得相较于滤波结果更精确的重力异常估计结果,提高了垂直加速度改正的精度。在对TFS算法和RTS算法的对比中,发现它们都可以对扰动噪声进行较好的压制,两种算法的精度基本相当,RTS算法的精度略微优于TFS算法。从性能、计算处理复杂程度等方面综合考虑,在航空重力测量数据处理阶段,可优先采用RTS算法进行平滑处理。
