型钢-混凝土组合梁桥面连续抗裂性能

陈 松，陈 真，郭 骞，冯博雅，孙路平，刘晓洲*

(1.大连大学建筑工程学院，大连 116622；2.辽宁省交通规划设计院有限责任公司，沈阳 110111)

传统组合梁的钢梁多采用焊接钢板梁，焊缝的存在不但增加了施工难度，还削弱了梁的局部受力性能。热轧型钢具有焊缝少、造价低、加工方便、力学性能好等优点，采用热轧H型钢代替传统的焊接钢板梁，能够提高桥梁建设工业化水平，是一项节能环保的新技术。受型钢制造技术所限，该类结构目前只适用于中小型跨径桥梁。为了推动型钢-混凝土组合梁桥的应用，提出了先简支后桥面板连续(简称桥面连续)的结构形式，该结构能一定程度上提高简支梁桥的整体性、提高行车舒适性、优化受力性能[1]。由于桥面连续结构薄弱，且处在梁端转动及纵向伸缩最大位置，受力情况复杂，在桥梁投入使用后不久便会出现开裂问题，提高该区域的抗裂性能是无缝桥梁设计的重要关注点。

按照中外相关研究，提高桥面连续抗裂性能的方法有优化结构设计、合理安排施工和采用高性能材料。邵旭东等[2-4]将箱型组合梁负弯矩区桥面板改用高性能混凝土，研究其受力性能，优化结构设计。刘双等[5]通过有限元分析，对组合梁矮塔斜拉桥剪力连接件的抗剪性能和桥面板的抗裂性能进行研究。吕沛文等[6]研究了负弯矩区的剪力件布置范围对该区域桥面板受力性能的影响。胡志坚等[7]对预应力钢-混箱型组合梁桥负弯矩区桥面板的破坏模式和裂缝分布进行了试验和理论分析。另有相关学者研究了通过优化施工方案改善组合梁桥负弯矩区受力性能[8-11]。受经济技术发展水平所限，钢筋混凝土梁桥在中国应用较广，目前中国对于桥面连续的研究绝大部分也为钢筋混凝土梁桥[12-14]，已有的关于组合梁桥的研究则集中在大跨径的钢板、钢桁架混凝土组合梁桥上，对于适用于中小跨径的型钢-混凝土组合梁桥的研究却鲜有涉及。

现首先对一片型钢-混凝土组合梁的桥面连续局部区域足尺模型开展结构试验，重点研究它的破坏模式及裂缝分布情况。在试验基础上，利用Ansys软件建立有限元模型并进行非线性分析，研究在改变剪力钉尺寸、剪力钉布置方式以及桥面板厚度情况下桥面连续的受力情况，并针对结果提出结构优化建议。

1 结构静力试验

1.1 试验模型

基于常规设计方法(刚接式桥面连续)，设计并制作桥面连续局部足尺模型，该模型主要由桥面板、钢梁、剪力钉、端横梁4部分组成。模型总长为6.22 m，其中钢梁和端横梁总计6.14 m,中缝长0.08 m;桥面板截面尺寸均为2 250 mm×220 mm，上下层均布置有纵向钢筋及横向分布钢筋，混凝土选用C40补偿收缩混凝土，钢筋材料选用HRB400；钢梁为热轧型钢，截面尺寸为588 mm×300 mm×12 mm×20 mm，材质为Q345D钢；剪力钉采用22 mm×120 mm的高强栓钉，纵向间距200 mm，横向间距110 mm；端横梁横截面尺寸2 250 mm×607 mm，混凝土及钢筋材料与桥面板所用材料相同，模型尺寸及截面配筋情况如图1所示。

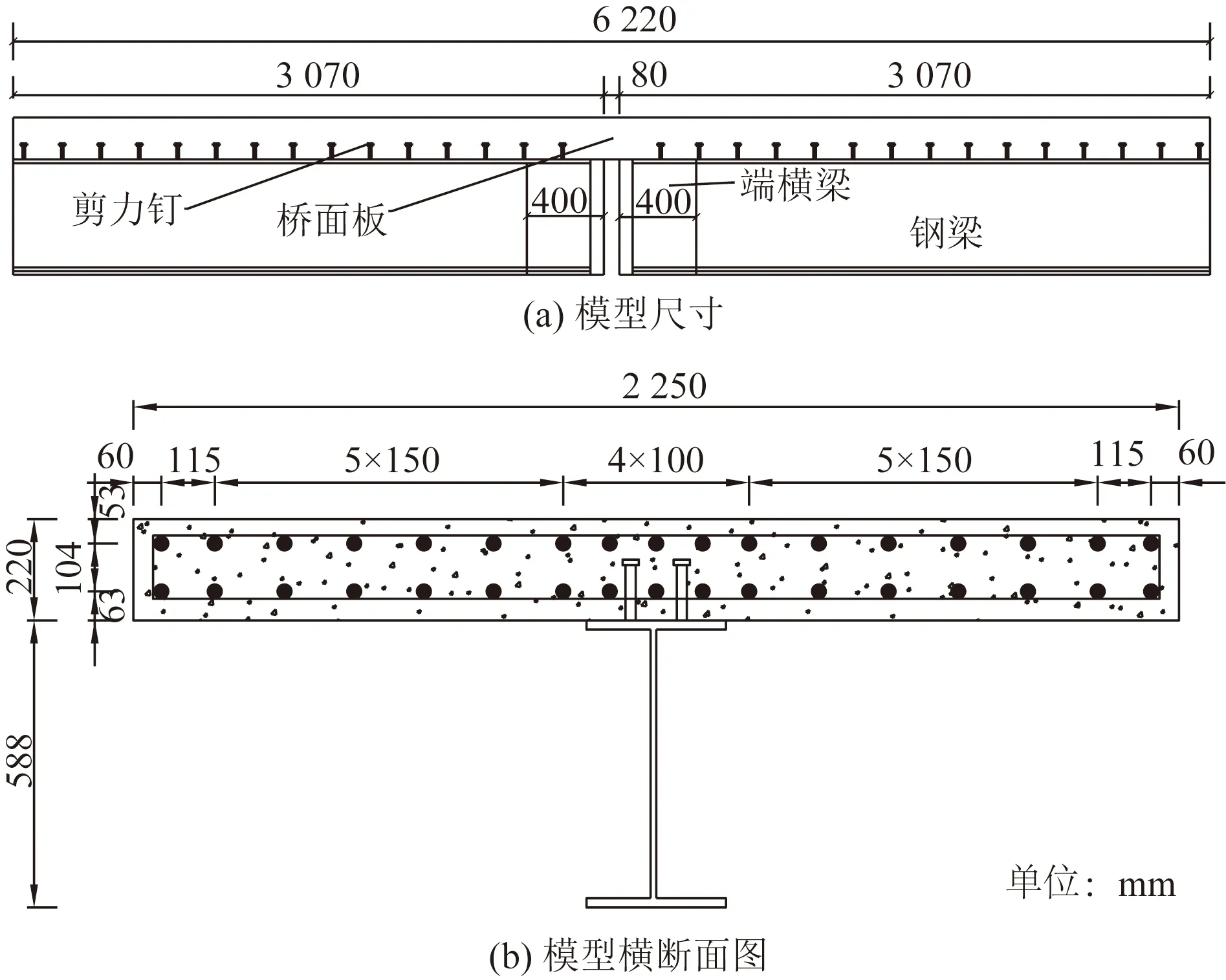
图1 模型示意图Fig.1 The sketch map of the experimental model

1.2 加载体系

由于桥面连续处在负弯矩区，受力情况复杂，为了模拟该位置的负弯矩效应，采用如图2所示的加载体系，通过悬臂加载方式实现桥面连续负弯矩的施加。该加载体系主要有压梁、反力架、垫块、支座及MTS加载装置5部分构成，其中：试件端横梁放置于具有一定高度的带支座的垫块上，使试件两端悬臂；压梁通过立柱与地面连接，从而对试件自由端进行约束；MTS与反力架连接，形成传力结构，对试件加载端施加荷载。

图2 加载体系示意图Fig.2 The sketch of loading system

1.3 测点布置

试验测试内容主要有桥面板裂缝分布、桥面板及钢梁的应变、试件竖向位移、试件滑移。试件外部应变采用自补偿弓形应变计测量，试件内部关键位置埋入钢弦式应变计；裂缝宽度使用智能裂缝测宽仪测量；位移及滑移值分别采用数显百分表、千分表测量，测点布置情况如图3所示。

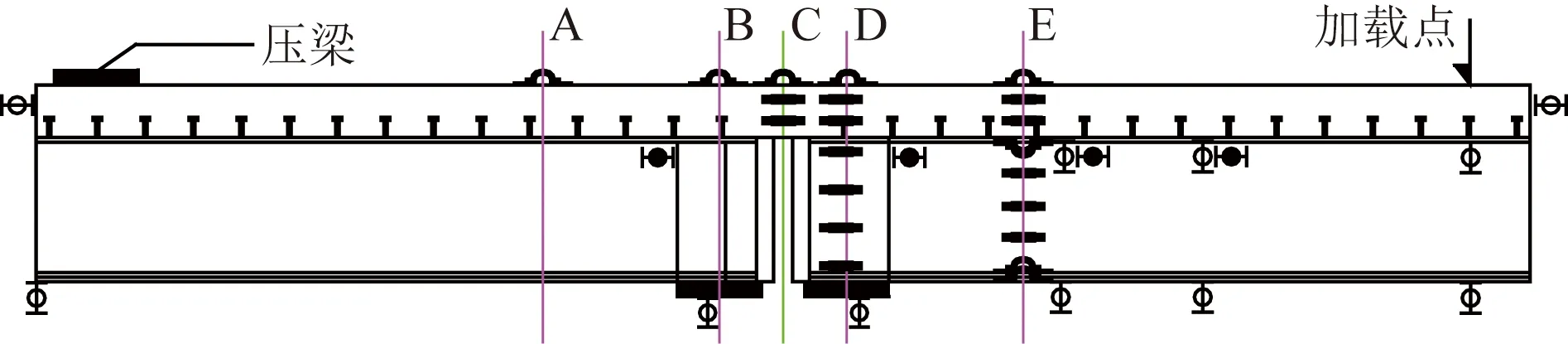
为百分表；为千分表；为表贴应变计图3 测点布置情况Fig.3 The arrangement of measurement points

1.4 试验描述

在试验开始前，进行仪器校准，仪器校准完毕后完成后，开始进入试验加载阶段，如图4所示。首先进行预加载，确认各仪器都正常工作情况下，开始进行正式加载。第一阶段按照每级5 kN进行，每级持载10 min；加载至30 kN时，A截面中心位置出现了第一条微裂缝，随着加载进行，裂缝不断增加；当加载至50 kN时，此时裂缝最宽达到了0.2 mm。此后按每级20 kN加载，随着裂缝的增加，试件刚度不断下降；当加载至230 kN时，挠度增加明显，为了保护仪器，此时撤掉百分表和千分表并改用位移加载；在竖向位移达到153 mm时，桥面连续处钢筋断裂，试验停止，记录此时荷载大小为336 kN。

图4 试验加载情况Fig.4 The loading of model

2 试验结果分析

2.1 滑移情况

提取了加载端梁纵向端横梁、E截面、中点位置的滑移量，分布情况如图5所示。从图5可以直观看出，试件在加载至90 kN左右时，滑移现象开始出现，从桥面连续附近到加载端附近呈现由大到小的趋势，且靠近桥面连续附近的滑移量远大于靠近加载端一侧的滑移量，说明桥面连续附近出现了应力集中现象。

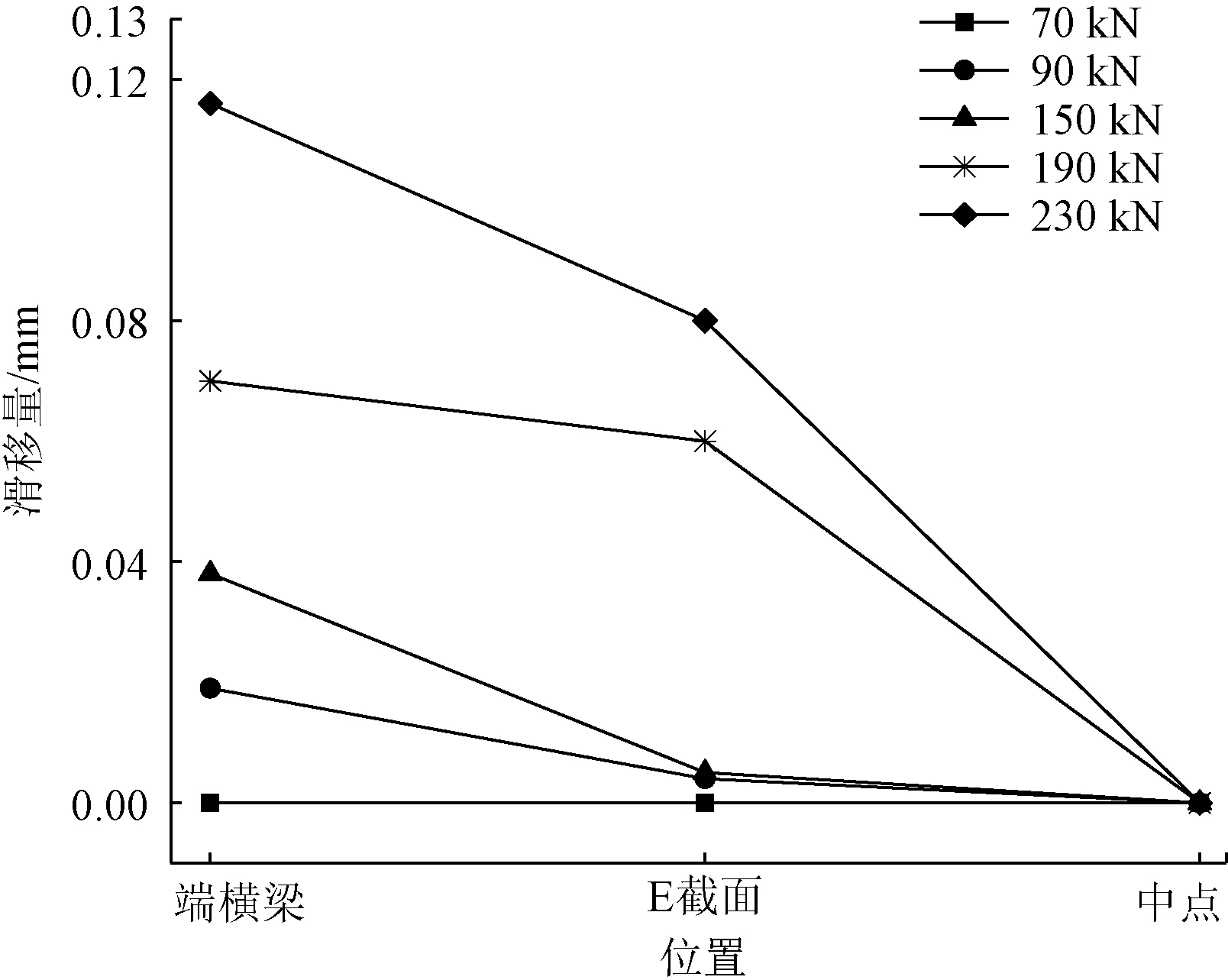
图5 各测点在不同荷载下的滑移量Fig.5 The slip of testing points in different load

由于230 kN时撤掉了千分表，在试件破坏后，利用精度为0.01 mm的数显游标卡尺对两端部最终滑移值进行测量，测量值如表1所示。

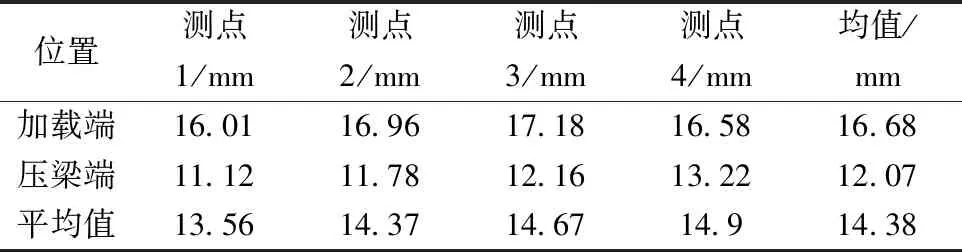
表1 试件两端最终滑移值Table 1 The ultimate slip of specimen

从表1中数据可知，试件两端滑移值均超过了10 mm，平均值为14.38 mm，按组合梁桥规范所列式(1)～式(3)计算所得极限滑移值为0.33 mm，试验所得值是该值的45.6倍。据此可以推测，在试件破坏时，试件的剪力连接件已经破坏，因此桥面连续附近的剪力连接件的类型和布置是影响桥面连续受力的重要因素。

(1)

(2)

(3)

式中：k、V、d分别为栓钉的刚度、正常使用状况下抗剪强度设计值和滑移量；Ec、fck、fc分别为混凝土的弹性模量、混凝土抗压强度标准值、混凝土轴心抗压强度设计值；As、fs分别为焊钉连接杆部截面面积、焊钉最小抗拉强度。

2.2 裂缝分布

试件的起裂点位于桥面板的C截面处，此后在该截面迅速形成1条贯穿裂缝，桥面板裂缝分布情况如图6所示，图中的裂缝均出现在桥面连续及其临近区域，其中通长裂缝4条，伴生裂缝5条。分析原因有以下3点：其一是由于该区域处在负弯矩区，梁端的转动及两端横梁的不同步位移均会通过剪力连接件带动桥面板协同运动，从而使桥面板顶面产生较大的拉应力，导致该位置桥面板过早开裂；其二是由于该位置结构薄弱，处在变截面区域，产生了应力集中现象；其三是由于该区域剪力连接件的破坏，导致该区域应力无法传递给其他区域，出现了裂缝较少的现象。

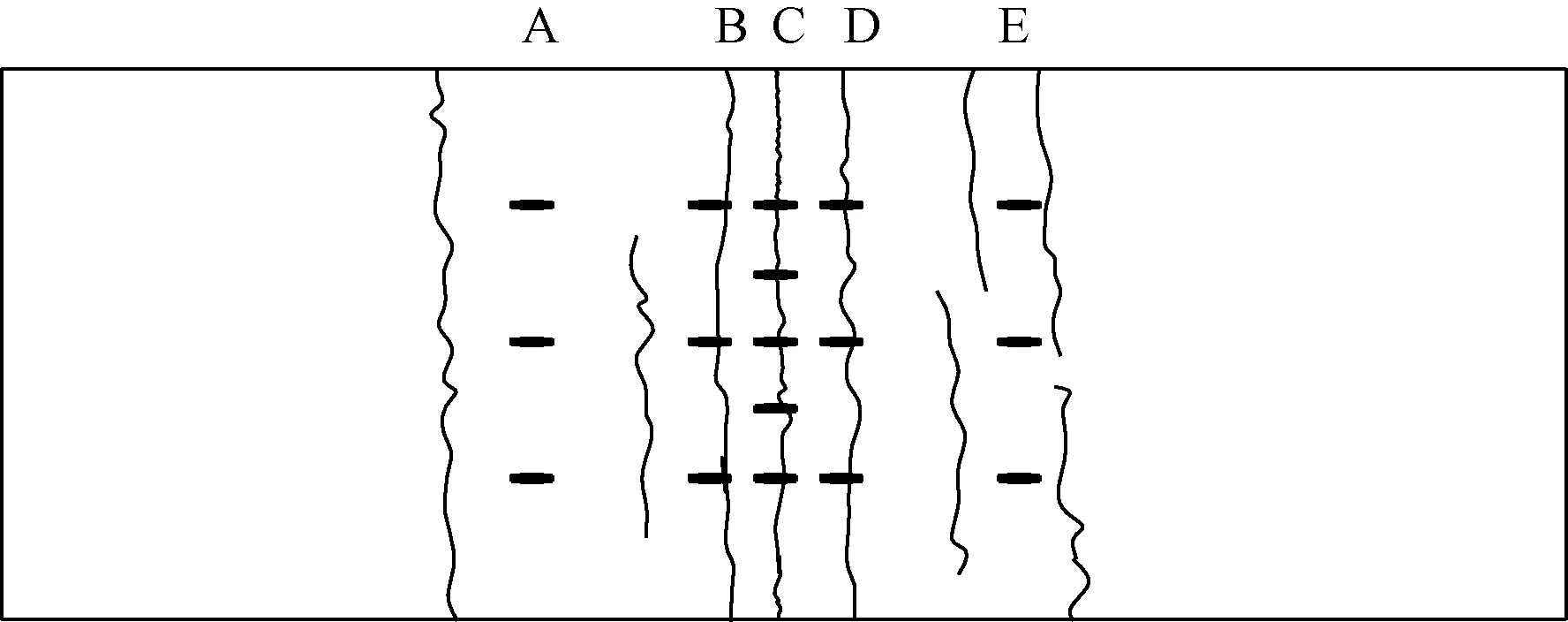
图6 桥面板裂缝分布情况Fig.6 The distribution of cracks on slab

2.3 应变分析

对桥面板上表面A、B、C、D、E共5个截面的应变数据进行处理，做出各荷载下桥面板纵向应变分布情况，如图7所示。总体趋势上看，桥面连续段顶部受拉，应变变化主要出现在B～D截面范围内，而A、E截面的应变量基本没有发生变化，这与观察到的裂缝1.5 m范围内现象基本吻合；在加载至50 kN时，C截面应变值发生了突变，此时C截面的应变值为839 με，这远远超过了混凝土的理论拉应变100 με，说明在30～50 kN的加载范围内，C截面最先出现了开裂，根据此刻C截面处的裂缝宽度达到了0.2 mm，可将50 kN定义为试件的开裂荷载；从图中可以看到C截面最先开裂，但是C截面处应变并未随着荷载的增大而增加，而是当荷载达到92kN后，出现了下降，分析原因是C截面的裂缝扩展到了弓形应变计支座，使得应变计出现了松弛，无法准确测量桥面应变；由试验加载系统并非对称系统，观察到B、D应变差异明显，靠近加载端截面的应变大于靠近压梁端截面的应变；总体上讲C、D截面的应变远大于A、B、E截面，这些截面中最大截面应变甚至达到了最小截面1 000倍，桥面连续区域出现了应力集中现象。

图7 各测点在不同荷载下的纵向应变Fig.7 The longitudinal strain of testing points in different load

3 有限元分析

通过结构试验得出剪力连接件的性能和布置方式会对型钢-混凝土组合梁桥桥面连续的抗裂性能造成影响，为了明确合理的剪力连接件类型和布置方式，在试验基础上，利用Ansys对组合梁桥面连续构造进行非线性分析。在确定了最优剪力钉方案后，建立了两跨先简支后桥面连续结构，找到合理的跨径和板宽，从而优化此类结构设计。

3.1 有限元模型

该模型中，钢梁采用shell181单元，桥面板采用考虑体积配筋率的solid65钢筋混凝土单元，栓钉采用combine39非线性弹簧单元，单元全局尺寸80 mm，有限元模型如图8所示。

图8 有限元模型Fig.8 The model of finite element method

3.2 材料模型

(1)混凝土材料。混凝土采用多现象随动强化模型MKIN，本构关系采用《混凝土结构设计规范》(GB50010—2015)中的拟合公式[15]，即

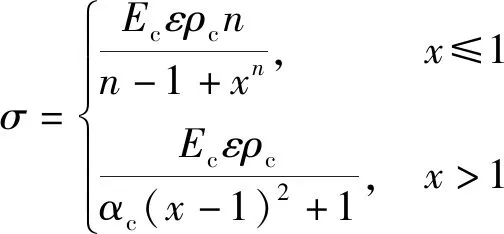
(4)

式(4)中：σ、ε分别为混凝土的应力及其对应的应变；ρc=fc/(Ecεc)为混凝土轴心抗压强度标准值，εc为抗压强度对应的峰值应变，取值为0.002，Ec为混凝土的弹性模量，取值为27 000 MPa；n=Ec/(Ecεc-fc)；x=ε/εc；αc取1.94。

(2)钢材。钢筋及钢梁均选用双线性等向强化模型BISO;钢筋的屈服强度为540 MPa,弹性模量为200 000 MPa；钢梁的屈服强度为345 MPa，弹性模量为200 000 MPa。

(3)栓钉。栓钉选用非线性弹簧单元，其剪力-滑移关系采用Ollgaard等提出的指数公式[16]，表达式为

V=Vu(1-e0.7s)0.8

(5)

式(5)中：V为栓钉所受剪力；Vu为栓钉抗剪极限承载力；s为滑移值。

3.3 边界条件及加载方式

在模型压梁对应位置设置竖向约束；在两支座对应位置按简支形式设置边界。加载方式与试验对应，即在加载处施加集中力，为了防止此处出现应力集中导致计算不收敛，在加载位置设置300 mm宽及30 mm厚的刚性加载垫块，并将该垫块和模型耦合，将集中力施加于刚性垫块上。

4 有限元分析结果

4.1 有限元模型验证

图9为试件加载端跨中截面的荷载-挠度曲线，从图9中可以看到：曲线的第一个拐点出现在30 kN附近，说明此时试件已出现了裂缝，试件从弹性阶段进入了塑性阶段；30 kN以后，曲线斜率不断增大，说明此后试件裂缝在不断发展，刚度在逐渐下降；由于270 kN时撤掉了位移采集装置，因此未能获取整个试验过程中的挠度随荷载的变化规律。在荷载增至120 kN以后，试验数据与有限元值出现了较大偏差，分析原因主要有以下两点：其一是由于混凝土是一种非均匀性材料，Ansys中没有有效模拟混凝土的行为本构模型；其二是由于试件在制作及养护过程中会出现一定的不可控缺陷。

如表2所示，模型关键数据的有限元值和试验值最大误差为9.5%，均小于10%。从图10可以看出，有限元的起裂位置位于桥面连续中缝位置，此后沿着中缝对称发展，这与试验观察到的开裂现象基本一致。此有限元结果进一步印证了利用此有限元模型进行非线性分析结果的合理性，可以按照此方法对桥面连续结构进行进一步研究。

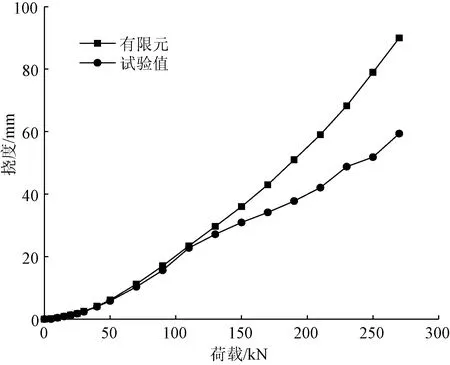
图9 挠度曲线Fig.9 The model of finite element method

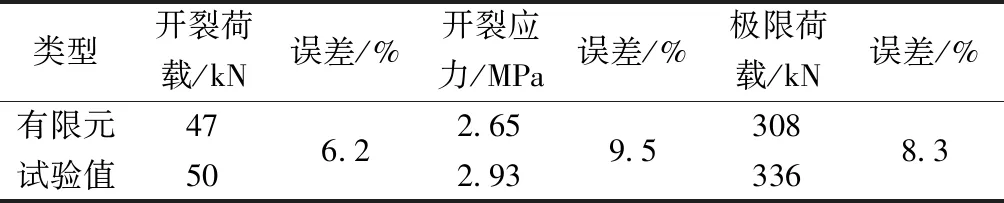
表2 荷载及应力对比Table 2 The comparison between force and stress

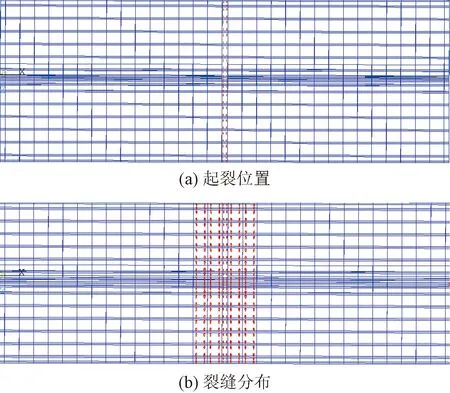
图10 有限元裂缝图Fig.10 The crack graph of finite element method

4.2 滑移对桥面连续抗裂性能的影响

为了研究组合梁的滑移对桥面连续影响，将钢梁与桥面板之间采用绑定接触模拟无相对滑移情形，当无滑移模型桥面板达到开裂荷载时，桥面板顶面的应力云图如图11所示，从图11中可知：两者的最大应力位置基本相同，均位移桥面连续中点附近；此时无滑移模型桥面的最大拉应力达到2.61 MPa，已超过混凝土的极限抗拉强度2.36 MPa,而此时考虑滑移模型桥面的最大拉应力为1.54 MPa,无滑移模型的最大拉应力是考虑滑移模型的1.69倍。然而，无滑移模型的极限荷载时417 kN,而滑移模型的极限荷载为308 kN,无滑移模型的极限荷载反而高于滑移模型109 kN。分析原因有以下两点：其一是滑移模型钢梁和桥面板是靠剪力连接件连接，和无滑移模型相比，其与钢梁的连接度较低，因此桥面板与钢梁的协同性较无滑移模型低，故此模型梁端的转动对桥面板的影响较弱；其二是滑移模型的破坏受栓钉破坏的影响(与试验结果基本符合)，因此其极限承载力受栓钉抗剪抗剪强度的影响较大，故极限荷载会低于无滑移模型。

4.3 栓钉间距及直径对桥面连续抗裂性能的影响

由于篇幅有限，后续分析将通过表格展示，按照试验结果和4.2节分析，组合梁桥桥面连续的受力情况与桥面板和钢梁之间的连接程度有很大关系，由于栓钉是一种实用性较强的剪力连接件，因此不考虑更换连接件类型，仅通过改变栓钉直径及布置间距来研究其对桥面板受力性能的影响。

4.3.1 栓钉间距

表3所示为不同栓钉间距下桥面连续的受力情况，从表3中可以得出，随着栓钉间距的增大，桥面连续处的应力减小，开裂荷载和极限荷载均有所增加。若桥面连续处不设置栓钉，和试验模型相比，桥面连续抗裂性能明显提高，开裂荷载是试验模型的1.6倍，极限荷载是试验模型的1.2倍；同等条件下，桥面连续处的应力均明显降低，其中压应力是试验模型的0.6倍，拉应力时试验模型的0.7倍。由于负弯矩区受力情况复杂，与4.2节类似出现以上现象是由于剪力钉的存在会带动桥面板随着梁端发生转动、上翘等运动，因此栓钉数量越多，桥面连续处与钢梁端的协同性便会更强，桥面连续更容易出现开裂现象。

图11 桥面板顶面应力云图Fig.11 The stress nephogram of top surface on slab

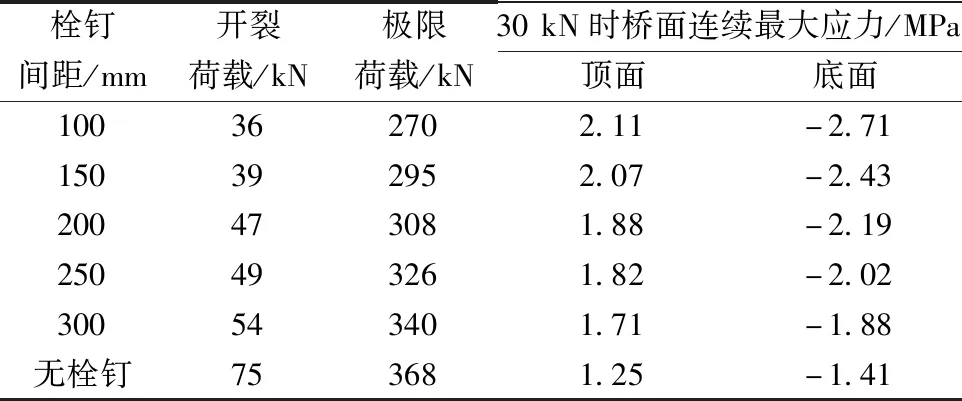
表3 不同栓钉间距下桥面连续的关键数据值Table 3 The key data of continuous slab in the different distance of stud

4.3.2 栓钉直径

按照《电弧螺柱焊用圆柱头焊钉》(GB/T 10433—2002)的规定，圆头焊钉的直径有10、13、16、19、22、25 mm，选取直径10、16、22 mm焊钉进行研究，分析结果如表4所示。

从表4可以看出：栓钉的直径对桥面板的开裂荷载及开裂前桥面板应力影响不大，但对桥面连续的极限荷载影响较大；随着栓钉直径的降低，桥面连续的极限荷载也呈现下降趋势；直径22 mm的栓钉荷载是直径16 mm和10 mm栓钉1.08倍和1.18倍。分析原因有以下两点：其一是由于桥面连续处的开裂荷载较小，开裂时栓钉并未发生较大变形，因此栓钉直径对桥面开裂荷载及应力影响不大；其二是由于后续荷载的增大，栓钉会发生较大变形，直径较小的钢筋抗剪刚度小，为桥面连续应力集中分担的能量较少，同时由于刚度的减小降低了钢梁和桥面板之间的连接性能，使梁端的转动和上翘变得更加明显。

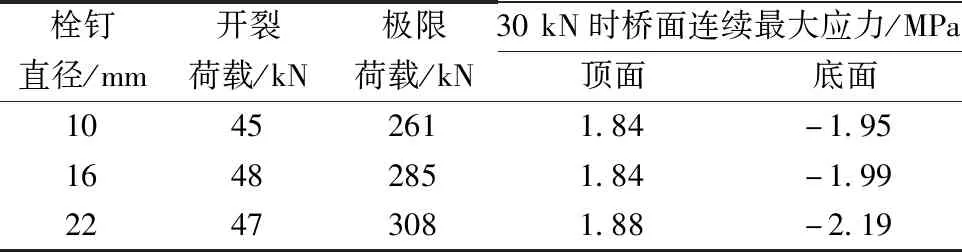
表4 不同栓钉直径下桥面连续的关键数据值Table 4 The key data of continuous slab in the different diameter of stud

4.4 厚度对桥面连续抗裂性能的影响

在分析剪力连接件对桥面连续抗裂性能影响的基础上，进一步研究不同桥面板截面尺寸对桥面连续抗裂性能的影响，为此分析了厚度为120、170、220、270 mm桥面连续的力学性能，为了贴近工程实际，用跨厚比进行表示，分析情况如表5所示。

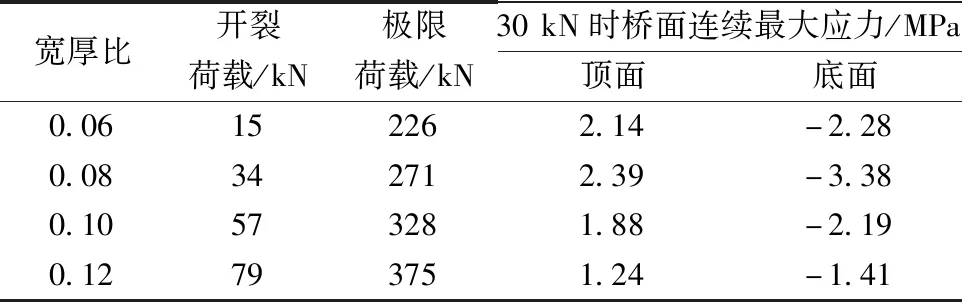
表5 不同桥面板厚度下桥面连续的关键数据值Table 5 The key data of continuous slab in the different thickness of slab

从表5中可以看出：随着桥面连续厚度的增加，其开裂荷载、极限荷载均有所增加，其中开裂荷载的最小和最大值之间相差64 kN，极限荷载最小和最大值之间相差149 kN；桥面连续处的应力值随着宽厚比的增加也呈现下降趋势；宽厚比为0.06与宽厚比为0.08的桥面连续相比应力有所增加，主要原因是由于30 kN时两者桥面连续均已开裂，混凝土的本构关系曲线进入了下降段，因此宽厚比为0.08的应力值会高于宽厚比为0.06的应力值。

5 结论

通过足尺模型结构试验和数值模拟方法对常规设计方法下型钢-混凝土组合梁桥面连续抗裂性能进行研究，得出如下结论。

(1)试验结果表明，常规设计方法下型钢-混凝土组合梁桥面连续在较低荷载内便会发生开裂，此类结构亟待进行优化设计；桥面板开裂范围位于桥面连续及其临近区域1.2 m范围内，通长裂缝只有4条，裂缝数量少；构件的桥面连续区域出现了应力集中现象，试件破坏位置位于桥面连续中缝处；试件破坏时剪力连接件已失效，试件两端出现了均超过10 mm的滑移量。

(2)按照试验及有限元分析结果，栓钉的种类和布置间距会影响桥面连续抗裂性能。当模型不考虑滑移时，开裂荷载降低了23 kN，极限承载力提高了109 kN；随着栓钉间距的增大，桥面连续的应力将随之减少，桥面连续的开裂荷载和极限荷载将会提高；桥面连续处不设置栓钉时，将会大幅提高其力学性能，其开裂荷载和极限荷载分别提高了67%和20%，桥面连续上下表面应力平均降低了40%；栓钉直径的改变对桥面连续的开裂荷载和开裂前应力影响不大，但对桥面连续开裂后的应力重分布和极限荷载影响较大，栓钉直径越小则桥面板极限承载力越小，直径每增大6 mm，桥面连续的极限承载力将提高约20 kN。

(3)桥面连续厚度将会对其力学性能造成影响。桥面连续厚度不宜低于150 mm，宽厚比不宜低于0.08，否则桥面连续结构将会出现过早开裂现象；宽厚比每提高0.02，桥面连续的开裂荷载和极限荷载将分别提高约22 kN和45 kN，桥面连续最大拉应力降低0.64 MPa，最大压应力降低0.7 MPa。

(4)按照试验和有限元分析结果对型钢-混凝土组合梁桥桥面连续的常规设计方法进行如下改进：建议将桥面连续的长度设置为1.2 m,并与钢梁做无粘接处理，此范围内的混凝土采用高性能混凝土；建议在规范允许范围内适当增加栓钉布置间距并采用直径25 mm栓钉；建议按照实际情况调整组合梁桥建筑高度，增大桥面板厚度。