基于负荷曲线分段的配电网无功优化策略
2021-09-26张国彦战文华卢文华余海英李华取
张国彦,姜 磊,战文华,卢文华,曹 磊,余海英,张 辉,李华取
(1.国网内蒙古东部电力有限公司赤峰供电公司,赤峰 024099;2.国网电力科学研究院武汉南瑞有限责任公司,武汉 430074;3.武汉大学电气与自动化学院,武汉 430072)
配电网是电力系统中直接向用户供电的重要环节,但其结构和运行特性决定了系统节点电压质量和线路损耗问题突出,特别是考虑到负荷波动的影响,往往难以达到系统运行的优质性和经济性要求[1-2]。所以有必要寻求有效无功优化补偿策略,以改善配网系统电压质量和提升运行经济性[3-4]。
无功补偿是常用以配网调压的措施,文献[5]以网损最小、电压波动最小和静态电压稳定裕度最大为目标,提出了基于多策略多目标粒子群算法的配电网无功优化方法。文献[6-7]以电压偏差和有功线损为优化目标,研究了串联补偿和并联补偿优化模型对配电网电压质量和网损的改善效果。文献[8-9]从网损、电压偏移和无功补偿投资最小等方面建立优化模型,并分别采用改进粒子群算法和NSGA-Ⅱ算法对模型进行求解。上述研究主要集中于在固定负载的单一断面下进行配电网的无功优化补偿,没有考虑负荷波动特性下的无功优化策略。为此文献[10]基于运行产生的数据进行历史场景匹配的控制策略,以进行无功控制和电压管理,文献[11]基于场景分析法,建立了并联电容器的优化配置模型,并将功率因素、谐振条件等作为约束条件,但基于场景生成的负荷波动性处理方法计算量较大,不具有很好的扩展性。针对负荷的随机波动特性,文献[12-13]采用负荷曲线分段的思想,提出了配电网分时段无功优化控制策略,具有较好实用性,但没有涉及无功补偿点的选择、各优化指标合理赋权等方面的研究,所建立的方法体系还不够完善。
鉴于此,现建立基于负荷分段的配电网无功优化补偿策略。首先,基于负荷曲线分时段静态化的思想,建立典型日负荷曲线的优化分段模型。其次,基于各负荷分段,进行无功补偿点的筛选,并以节点电压平均偏移和运行网损为优化指标,建立求取每个分段内无功补偿方案的优化数学模型。采用基于分解的多目标优化(multi-objective evolutionary algorithm based on decomposition,MOEA/D)算法对所建立的优化模型分别进行求解可得出负荷分段结果及各分段对应的最优补偿方案。最后,以IEEE 33节点配网系统算例仿真分析,验证所建立配电网无功优化策略的可行性和有效性。
1 负荷曲线优化分段模型和无功补偿点筛选
1.1 负荷曲线优化分段模型
基于负荷曲线分时段静态化思路,把连续典型日负荷曲线进行合理的分段,将每个分段内负荷视为确定负荷求取无功优化补偿方案,将有效减少并联补偿装置投切次数和减少设置不同的补偿容量等级,具有更好的合理性和经济性。理论上划分的时段数越多,改善电压质量和降低运行网损的效果将越好,但避免使设备动作过于频繁,影响设备使用寿命和影响经济性,分段数可依据实际情况合理设置。
采用多目标优化的方法对负荷曲线进行分段处理,其中优化目标为表征不同时段负荷的平均值之间离散性的指标M1最大,表征属于同一时段内负荷离散性的指标M2最小。若负荷曲线分段数为NL,为使优化目标方向一致,对优化目标M1取倒数处理,即负荷曲线优化分段的目标为
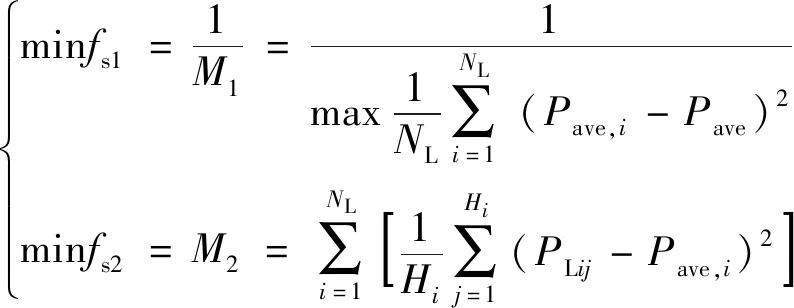
(1)
式(1)中:Pave为所有时刻负荷的平均值;Pave,i为第i个分段内的负荷平均值;PLij为第i个负荷分段内第j个负荷点的负荷大小;Hi为第i个分段内的负荷点总数。
优化分段后每个分段内各时刻的负荷值取该分段的负荷平均值。当划分为NL个负荷分段,则有NL-1个负荷分点,即优化控制变量为t1,t2,…,tN-1,其中负荷分点不能超出全天范围24 h,且分点之间互不相等,则控制变量约束为
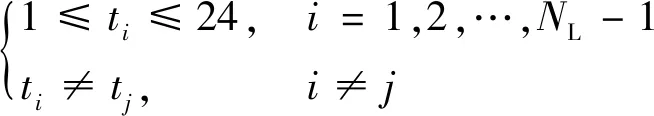
(2)
1.2 无功补偿点筛选确定
针对实际电网节点数规模庞大,若不筛选确定固定的补偿点将会导致优化效率降低,优化效果不理想,另一方面,在一天的24 h周期内,从合理性和投资经济性角度考虑,不同负荷分段内的补偿点应该相同,以减少无功装置的建设点。为此通过综合考虑平均节点电压偏移灵敏度和网损灵敏度进行无功补偿点的筛选确定。其中在每个负荷分段下的平均节点电压偏移灵敏度和网损灵敏度分别定义为
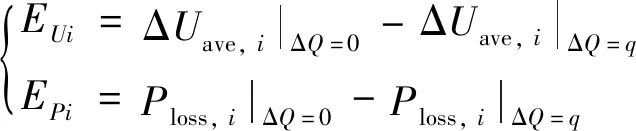
(3)
式(3)中:EUi和EPi分别为在节点i没有无功扰动和注入无功扰动ΔQ=q后引起的系统平均节点电压偏移和网损变化量。其中ΔUave,i和Ploss,i的计算表达式[14]分别为
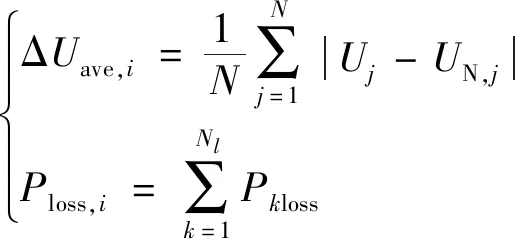
(4)
式(4)中:ΔUave为系统平均节点电压偏移;N为系统节点总数;Ui和UN,i分别为第i个节点的实际电压和额定电压;Ploss为系统运行总网损;Nl为系统支路总数;Pkloss为系统第k条支路的有功损耗。
在灵敏度进行加权之前,针对各指标在数量级或方向上存在不一致,采用式(5)所示方法对方案i下的负向或正向指标进行标准化处理。
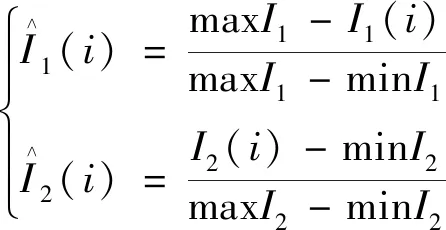
(5)

其中平均节点电压偏移灵敏度和网损灵敏度都为正向指标,越大越好,标准化处理后对每个负荷分段下进行无功补偿点筛选的综合灵敏度指标定义为
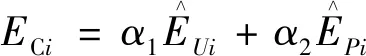
(6)
基于上述方法,可得出每个负荷分段下的全网无功补偿点的综合灵敏度排序,结合配电网结构特性和无功分区就地补偿的原则,可依据不同的馈线进行节点分区,在每个馈线上的节点中选取综合灵敏度较大节点作为此馈线上的无功候选补偿点。即针对有NL个负荷分段,每条馈线可得出NL组备选补偿点方案,选取最优补偿点出现次数最多节点作为该馈线区全天最优补偿点。
1.3 基于组合赋权法的权重确定
对无功补偿点筛选过程中指标权重α1和α2的赋权,采用能兼顾主客观因素的组合赋权法,具有合理全面性。其中采用改进的层次分析法(analytic hierarchy process,AHP)进行主观赋权,可较好地处理传统AHP在实际评价过程中面临效率低、易出现不满足校验等问题[15],客观权重采用反熵权法计算,能克服熵权法确定权重时个别权重过大或过小的极端情况[16]。改进层次分析法和反熵权法原理步骤如下。
1.3.1 改进层次分析法
设共有m项待赋权指标,按照重要程度不减的原则,专家对指标的相对重要性行进行式(7)所示的排序,其中重要度具体数值可参考表1。
x1≥x2≥…≥xm
(7)
表征xi和xi+1的相对重要关系记为si,由此得判断矩阵W中各元素为

表1 指标相对重要程度的标度Table 1 Scale of relative importance of indexes

(8)
据此可得各指标的主观权重为
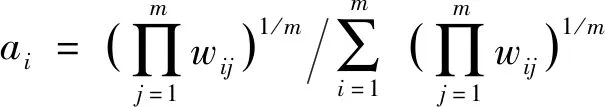
(9)
1.3.2 反熵权法
设指标样本数为n,则指标j的信息熵为
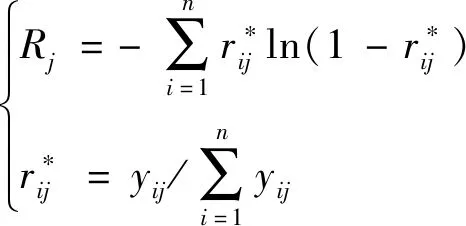
(10)
式(10)中:yij为对原始决策矩阵进行规范化操作后矩阵中的元素值。根据式(10)可确定各指标的客观权重bj为
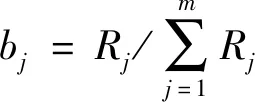
(11)
1.3.3 综合权重确定
在分别得出主客观权重基础上,采用乘法加权计算指标综合权重,公式为
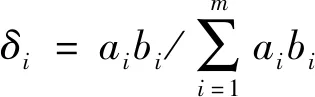
(12)
式(12)中:δi为指标i的综合权重。
2 无功优化数学模型
无功补偿目的主要为改善电压质量和降低运行网损,采用如式(4)所示的系统平均节点电压偏移和系统运行网损指标作为每个负荷分段无功补偿的优化目标,即
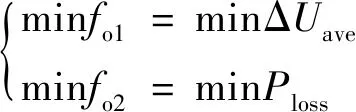
(13)
在每个负荷分段的优化过程中,设定约束条件分别为节点功率平衡约束、发电机有功无功出力约束、节点电压上下限约束、线路最大输送功率约束,以及加上并联补偿容量上、下限值等控制变量约束共同构成优化模型的约束条件,如式(14)所示。
(14)
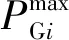
3 基于负荷曲线分段的优化策略
3.1 优化模型求解及最优解集评估
MOEA/D算法思路为将多目标优化问题分解为一组单目标优化问题从而进行同时优化,收敛速度快,相较于NSGA-Ⅱ算法具有计算复杂度低、优化效果好的特点,算法具体细节可参见文献[17]。前文所建立的优化模型都采用MOEA/D算法进行求解,从而得出Pareto最优解集。其中为增强MOEA/D优化算法的局部搜索能力和提升优化效果,对进化操作后的个体元素vi,采用式(15)所示的高斯变异方法以增加种群多样性[18]。
(15)
式(15)中:rand1为产生满足补偿容量上下限约束的随机数操作,共产生Nc个数;Pi为变异率;δ2为给定高斯变异方差;rand2为产生服从高斯分布的随机数操作。
基于求解负荷优化分段模型和求解无功优化模型得出的Pareto最优解集,采用1.2节和1.3节中的指标处理方法和组合赋权评估可得出最优的负荷曲线分段方案和无功补偿参数方案。即负荷优化分段和每个分段下的无功补偿优化综合目标函数可表示为

(16)
式(16)中:ε1、ε2和β1、β2均为权重因子,且ε1+ε2=1,β1+β2=1。
3.2 分时段无功优化策略流程
基于上述所建立的方法,所提的无功优化策略的具体步骤如图1所示。

图1 分时段无功优化补偿整体流程Fig.1 Overall flow chart of reactive power optimization compensation in different periods
4 算例验证
4.1 IEEE 33节点算例
4.1.1 算例参数和负荷曲线分段处理
采用IEEE 33节点配网系统作为算例仿真分析,系统拓扑如图2所示,系统包括4条馈线,馈线编号如图2所示。系统节点电压额定值为1.0 pu,pu为标幺值单位,功率基准值设为100 MW,其中系统结构参数保持不变,依据某地区典型日负荷曲线变化规律,结合原系统的负荷规模,模拟出系统的典型日负荷曲线如图3所示。此外,设置MOEA/D算法最大迭代次数为100,变异率设为0.8,高斯变异方差设为0.075。在利用改进AHP主观赋权时,优化分段指标M1相对M2的重要度取1.0,平均电压偏移指标相对网损指标的重要度也取1.0(下同)。设置负荷分段数NL为5,采用所建立的负荷优化分段方法得出的负荷分段曲线如图3所示,其中对负荷分段最优解集评估的权重因子ε1、ε2分别为0.533和0.477,优化目标值M1和M2分别为0.465 9和0.528 4。
由图3可看出,把全天24 h分为5个时段分别为:1~6 h时间段,7~10 h时间段,11~16 h时间段,17~21 h时间段,22~24 h时间段。基于所得到的负荷曲线分段结果,没有无功补偿时各分段下对应的系统各节点电压分布如图4所示,可看出每个负荷分段下的电压水平都偏低,尤其是线路末端节点,最低电压节点已超出配电网的允许电压偏移下限0.93 pu,所以有必要进行无功补偿实现电网电压质量的改善。
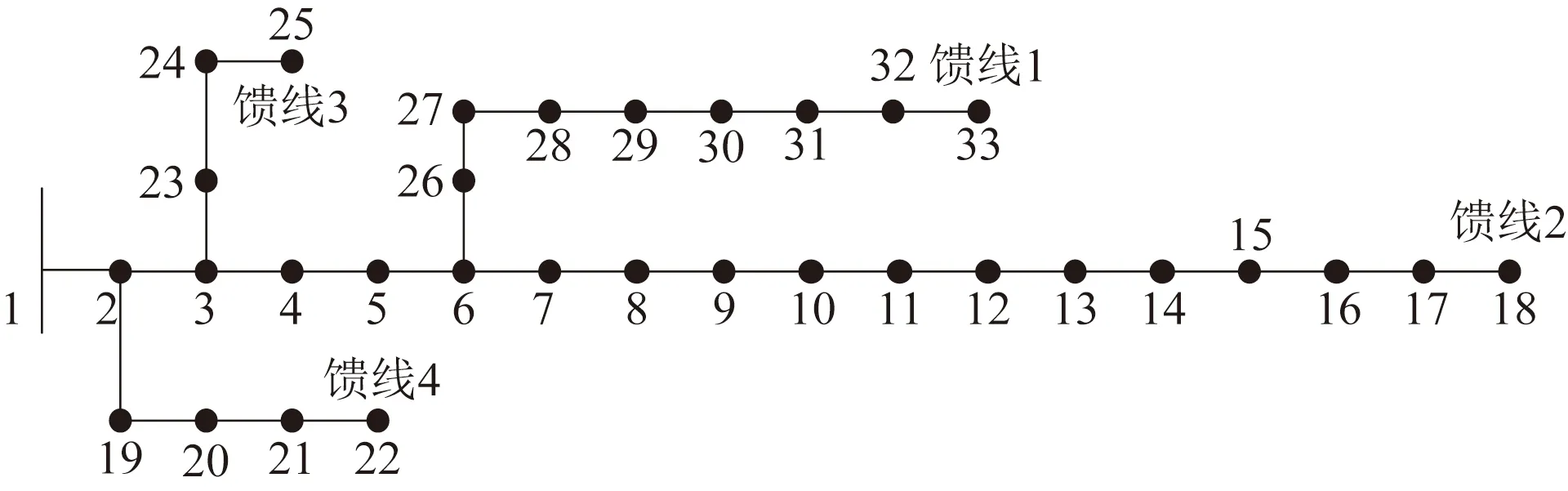
图2 IEEE 33节点系统结构图Fig.2 IEEE 33 node system structure diagram
4.1.2 无功补偿点筛选
设置两组无功补偿装置的容量优化确定,结合图2所示的系统结构分析,无功补偿点分别选择馈线1和馈线2区域。采用所建立的无功补偿点确定方法,取无功扰动ΔQ=0.005 pu时,在每个负荷分段下,根据馈线1和馈线2上综合灵敏度排序结果选取前4节点及目标值、每个分段的权重因子如表2所示。
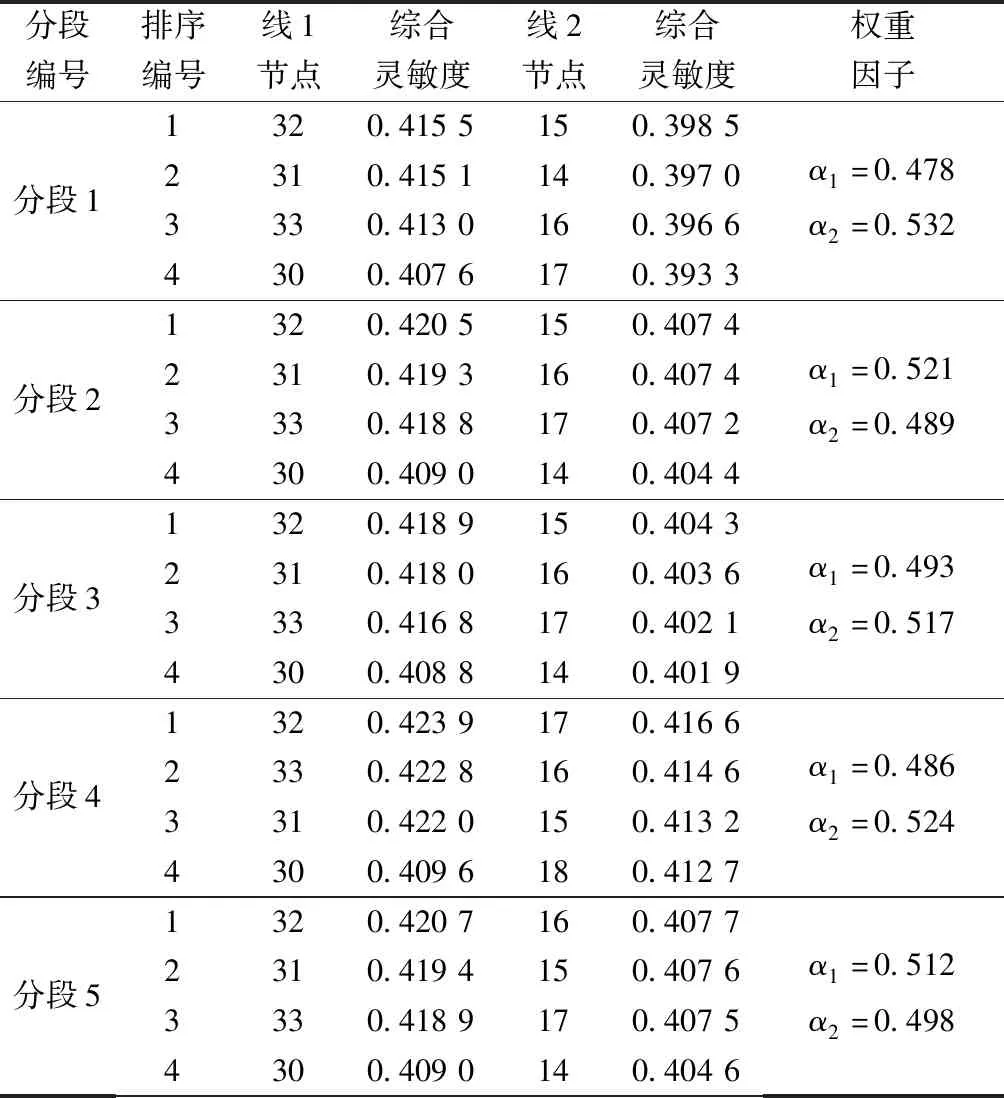
表2 各负荷分段下的综合灵敏度排序Table 2 Comprehensive sensitivity ranking under different load sections
由表2中结果分析可知,馈线1上的最优无功补偿点在每个分段下都为节点32。馈线2上在分段4和分段5的最优补偿点分别为节点17和节点16,其余分段最优补偿点都为节点15,所以综合对比分析选用的无功补偿点分别为馈线1的节点32和馈线2的节点15。
4.1.3 无功优化补偿求解
无功优化补偿过程中,设定电压允许上下限分别为1.07 pu和0.93 pu;支路最大传输功率为2 MW;无功补偿容量上下限分别为2 Mvar和0.5 Mvar。基于MOEA/D算法对优化模型求解后得出每个分段下的无功优化补偿方案及最优目标值如表3所示。
基于表3优化结果,每个负荷分段内补偿前后平均电压偏移对比和网损对比分别如图5(a)和图5(b)所示。由此看出,与没有无功补偿相比,每个负荷分段进行无功优化补偿后的节点电压平均偏移和网损都有了不同程度的减小,使电网电压质量更优和运行经济性提升。
此外,每个负荷分段内补偿后的系统各节点电压分布如图6所示。与图4的对比分析可看出,无功优化补偿后系统的整体电压都得到了有效提升,并且各分段的最低点电压都在0.93 pu以上,满足配电网的电压偏移要求。
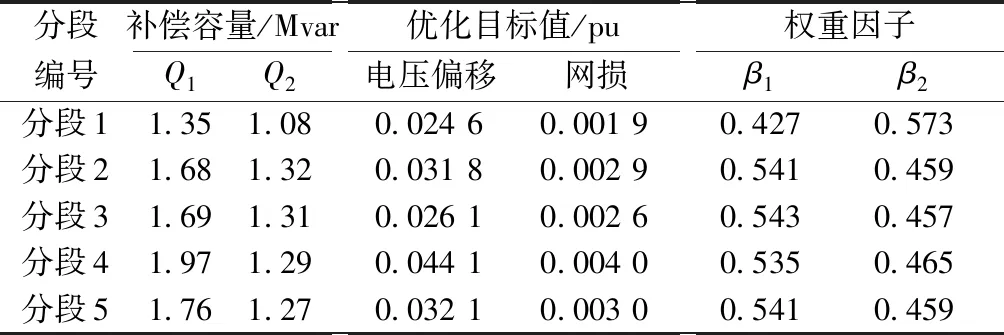
表3 无功补偿参数及对应优化目标和权重Table 3 Reactive power compensation parameters and corresponding optimization objective and weight
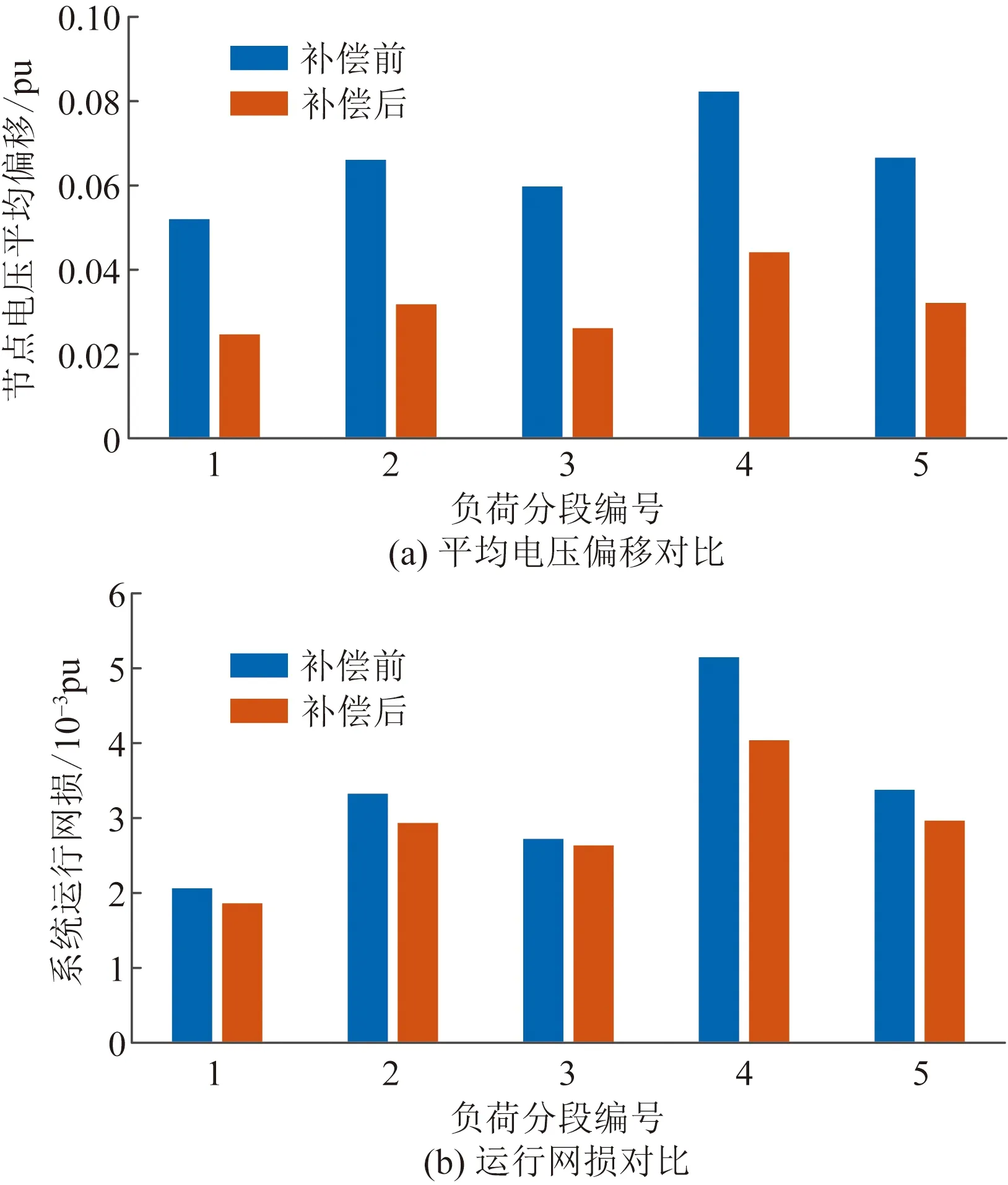
图5 无功补偿前后各分段的平均电压偏移和运行网损对比Fig.5 Comparison of average volage offset and active power network losses before and after reactive power compensation

图6 无功补偿后各分段下的系统电压分布Fig.6 system voltage distribution under each segment after reactive power compensation
4.1.4 无功优化策略有效性验证
上述分析可知,基于负荷分段进行无功优化补偿后,在每个分段的确定负荷下都有较好补偿效果。为验证此优化策略在全天的负荷变动过程中对电网电压和网损的控制效果,使系统负荷按图3所示在全天24 h周期内进行变化,采用基于负荷分段方法确定的无功补偿方案进行补偿,在此过程中与没有无功补偿下的平均节点电压偏移和系统运行网损对比如图7(a)和图7(b)所示。
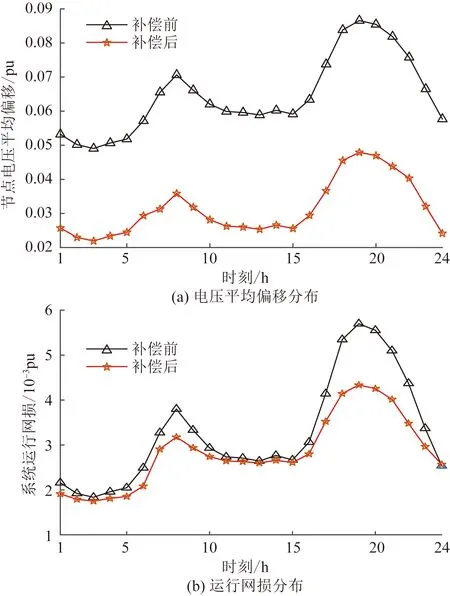
图7 无功补偿前后电网全天电压平均偏移分布和运行网损分布Fig.7 Distribution of network loss of average deviation of voltage and active power operation in whole day before and after reactive power compensation
图7分析可得出,采用基于负荷分段方法所确定的无功优化补偿方案,相较于不进行无功补偿在全天内的电压平均偏移和系统运行网损都更小,且只用设置5组不同容量大小的无功补偿方案就可取得较好的全天补偿效果,验证了所建立无功优化策略具有较好的合理性和可行性。
4.2 实际电网算例
为进一步验证所提优化策略的有效性和可靠性,采用内蒙古长胜变电站出线系统模型进行仿真分析,该系统为典型10 kV配网系统,系统拓扑如图8所示,将长胜变节点设为平衡节点,电压有名值10.5 kV。另外基于系统日负荷分布曲线,当设定负荷分段数为4时,采用所建立的优化分段方法,日负荷曲线和得出的负荷优化分段结果如图9所示。
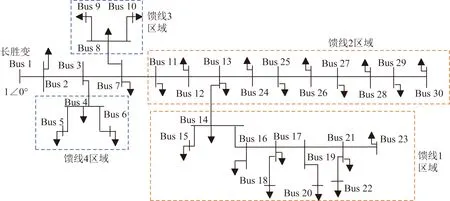
图8 实际电网拓扑图Fig.8 Topology diagram of actual power network

图9 系统日负荷曲线及分段结果Fig.9 Daily load curves and segmentation results of the system
设定无功补偿容量寻优范围为1~100 Mvar,求解无功补偿优化模型,得出每个分段下的无功优化补偿方案如表4所示。
另外由系统拓扑结构分析可将系统主要分为4个馈线区域,如图10所示。设定两组无功补偿装置容量优化确定,可考虑分别在馈线1和馈线2区域确定最优无功补偿点。取无功扰动ΔQ为5 Mvar,基于所建立的补偿点筛选方法,可得出全天范围内馈线1和馈线2最优补偿点分别为Bus22和Bus30。同时在每个负荷分段下,无功优化补偿后,线路电压都得到了不同程度提升,电压质量改善效果明显,且线路末端区域节点电压都在10 kV附近,电压分布更为合理。
当系统负荷按图9所示在全天周期内进行变化,采用所建立优化策略进行控制与没有无功补偿下的平均节点电压偏移和系统运行网损对比如图11所示。分析同样可得出相较于不进行无功补偿,在全天内的电压平均偏移和系统运行网损都更小,因此实际电网中也可验证所建立的无功优化策略具有合理性和可靠性。

表4 无功优化补偿方案Table 4 Reactive power optimization compensation scheme
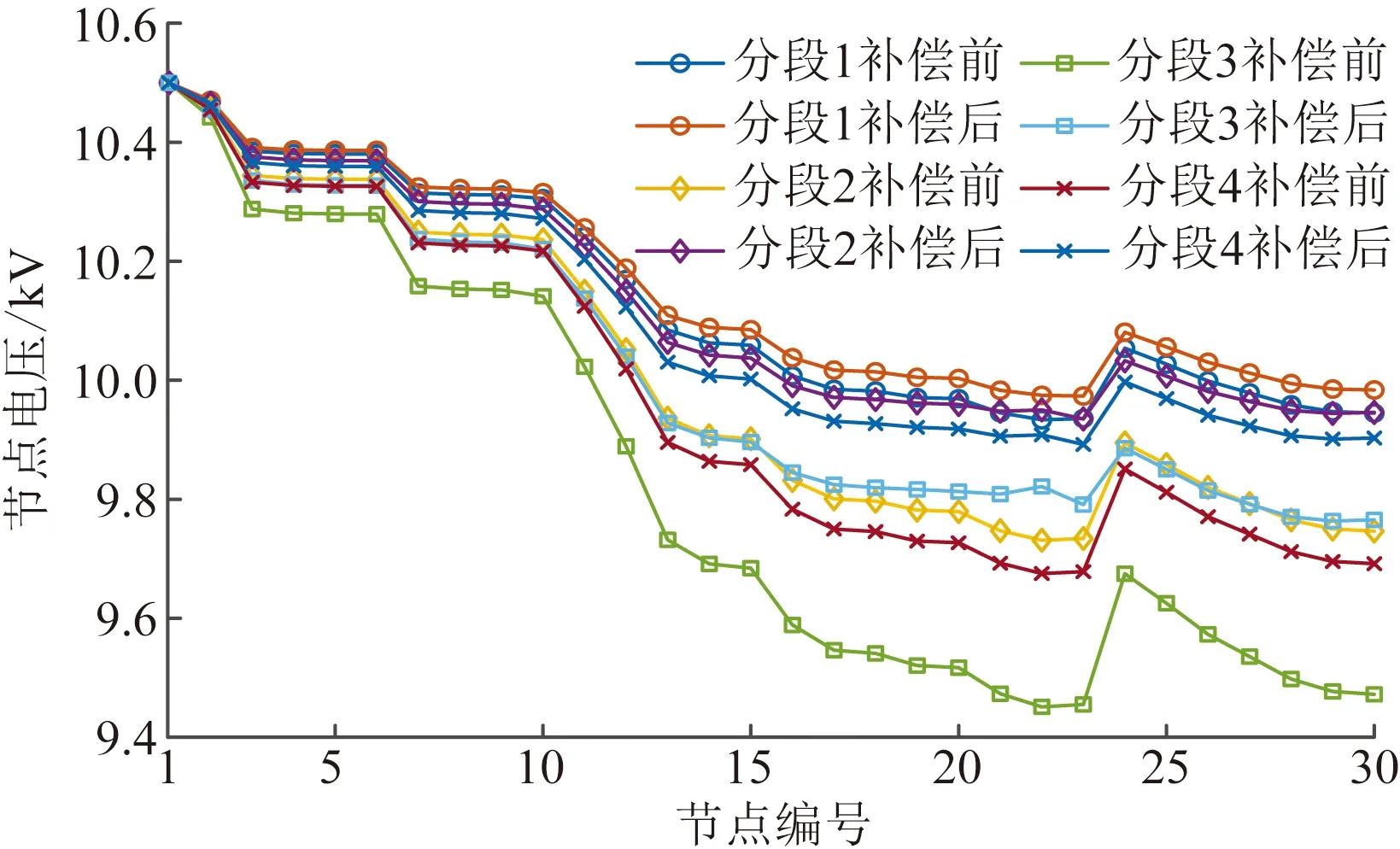
图10 各负荷分段下无功补偿前后节点电压分布Fig.10 Voltage distribution before and after reactive power compensation under each load segment
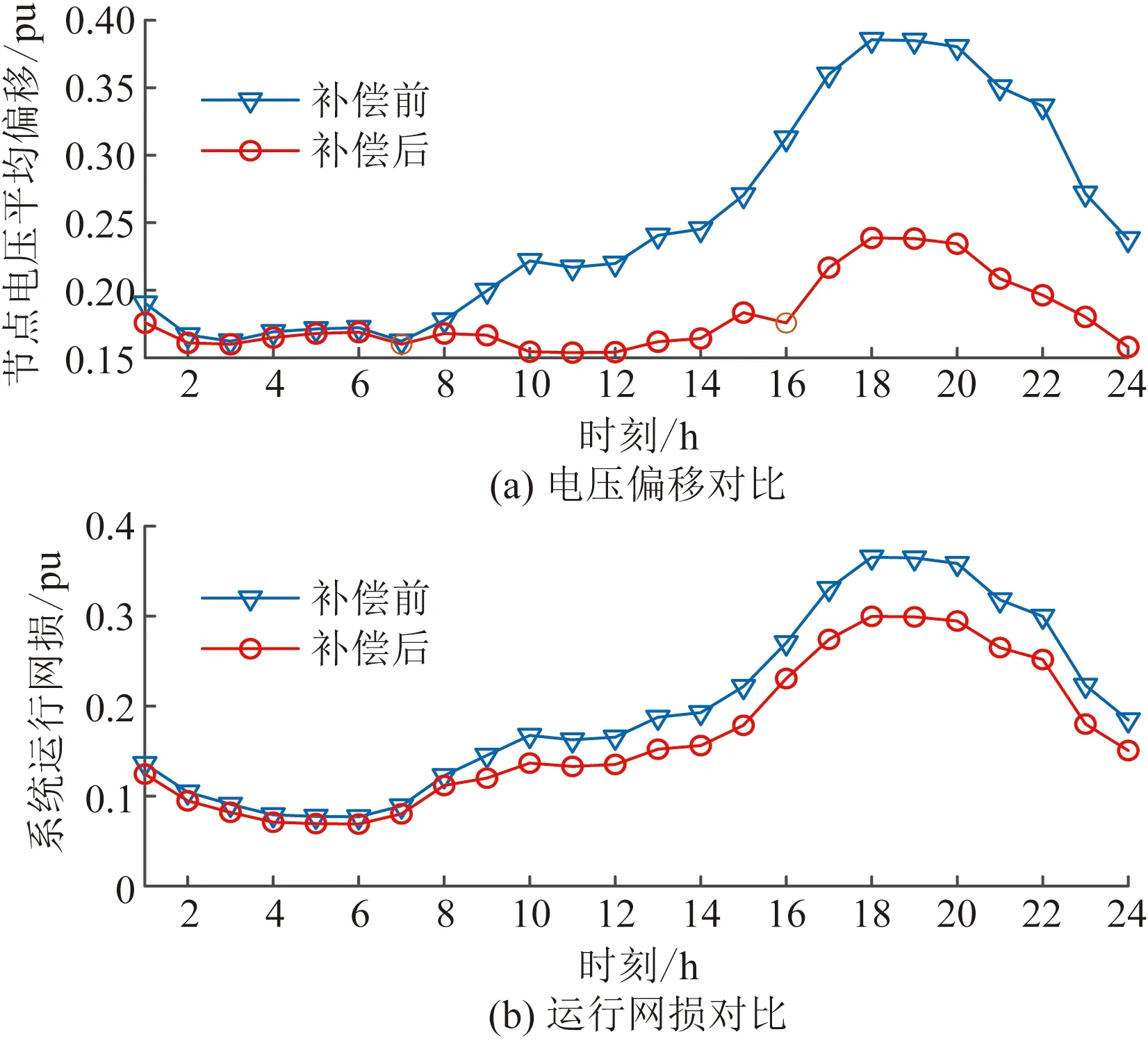
图11 无功补偿前后电网全天运行情况对比Fig.11 Comparison of all day long operation of power grid before and after reactive power compensation
5 结论
通过典型日负荷曲线的优化分段、无功补偿点的筛选确定、以及基于负荷分段结果进行无功优化等步骤,通过采用改进MOEA/D算法对优化模型求解,系统地建立了完善的基于负荷曲线分段的配电网无功补偿优化策略。以IEEE 33节点配电网系统和实际电网算例验证分析得出:基于负荷曲线优化分段,能较好地处理电网负荷的随机波动性。通过主客观组合赋权综合平均电压偏移和网损灵敏度指标对无功补偿点进行筛选,可得出合理有效的无功补偿点。依据所建立的分时段优化补偿策略,在针对全天范围内的负荷波动,可较好地控制电网电压质量和保证系统运行经济性。
主要分析了基于历史典型日负荷曲线进行配电网无功优化配置,此外所提方法流程也可用于根据电网未来某日的负荷预测曲线或者针对中、长期负荷预测结果曲线采用优化分段的思路作出相应的无功预配置。
