结合旋量理论和代数方法的六自由度机械臂逆运动学求解算法
2021-09-26陈禹含韩宝玲王善达许仕杰
陈禹含,韩宝玲*,王善达,许仕杰,刘 杨
(1.北京理工大学机械与车辆学院,北京 100081;2.北京理工大学机电学院,北京 100081)
实现轨迹规划[1]、运动控制[2]等典型机器人功能的前提是解决逆运动学问题。该问题是已知末端执行器位姿,求解关节变量值。因为逆运动学求解存在非线性和多解的问题,所以很难找到一种适用于不同构型机器人的逆运动学解析的求解算法[3]。
对机器人运动学的描述方法有Denavit-Hartenberg参数法[4]和指数积方法[5]。伞红军等[6]、宁祎等[7]和张震等[8]利用前者的描述方法对机器人进行建模并完成逆运动学求解。但是该描述方法存在描述参数复杂且模型表述不唯一等缺点。而后者描述方法具有建模过程简单、描述参数少等优点,且该方法在进行逆运动学求解时具有明确的几何意义,所以指数积方法越来越受到欢迎。赵荣波等[9]及敖天翔等[10]利用旋量理论和代数消元相结合提出了6-DOF机器人逆解算法,该方法适用于末端3个关节轴线相交于一点的串联机器人。李立君等[11]基于旋量理论对6-DOF混联机械臂进行逆运动学求解,该方法可以稳定得出10组工作目标位置信息对应的关节值。卢喆等[12]将几何法与旋量理论相结合推导6-DOF串联机器人逆运动学,该方法是采用几何法解决前3个关节轴线不相交的问题,采用Paden-Kahan子问题的方法求解后3个关节轴线交于一点的问题。Sung等[13]和Wang等[14]将3类Paden-Kahan子问题不同组合,设计出几种新的逆运动学子问题,并利用旋量理论进行分析求解,该结果具有一定的通用性。
目前各位学者的求解逆运动学的方法大多是适用于末端3个关节轴线相交于一点的构型,该构型常用于工业机械臂中,但是另一种满足Pieper准则[3]的构型,即具有相互平行的3个相邻关节轴的机械臂,利用旋量理论求解该逆运动学却少有研究。针对这一问题,现使用旋量理论与代数相结合的方法求解具有相互平行的3个相邻关节轴的串联式机械臂逆运动学问题。
1 预备知识
1.1 旋量理论数学基础
刚体运动可由4×4的齐次变换矩阵T表示,该变换矩阵由旋转变换R和平移变换P组成。根据Chasles定理[15],任意刚体移动都可以表示为绕某一转轴的旋转和沿着该轴平移的组合运动,该运动称为螺旋运动,且其无穷小量为运动旋量[9]。
运动旋量Si由旋转角速度ωi和平移线速度vi组成
(1)
式(1)中:vi可以表示为
vi=-wi×qi
(2)
式(2)中:qi为Si转轴上的任意一点。Si的矩阵形式为
(3)
式(3)中:[wi]为wi的斜对称矩阵;0为1×3维零向量。
基于旋量理论,计算n自由度串联式机械臂末端执行器位姿Te的公式[5]可表示为
Te(Θ)=e[S1]θ1…e[Sn-1]θn-1e[Sn]θnM
(4)
式(4)中:M为末端执行器的初始位姿;θi为机械臂各关节角度;Θ为由机械臂各关节角度组成的向量,表达式为
(5)
[Si]θi的指数形式可以表示为
(6)
式(6)中:0为1×3的零向量;Ri(θi)和Pi(θi)的表达式为
Ri(θi)=e[wi]θi=
I+[wi]sinθi+[wi]2(1-cosθi)
(7)
Pi(θi)=[(I+[wi]2)θi+[wi]×
(1-cosθi)-[wi]2sinθi]vi
(8)
式中:I为3×3的单位矩阵。
1.2 Paden-Kahan 子问题
Paden-Kahan子问题是基于旋量理论的指数积公式,用几何方法求出绕轴的旋转角度[13]。基于旋量理论的运动求解可以分为3 类Paden-Kahan子问题,Murray等[15]对这3 类子问题做了详细的介绍。这里仅介绍求解过程中所用到的第1类子问题。
第1类Paden-Kahan子问题是关于单一转轴旋转,如图1所示。具体过程是绕运动旋量S旋转θ角度,使点q1旋转至点q2。S中向量w为单位向量,且代表旋转方向。那么在已知运动旋量S和点q1、q2坐标的前提下,旋转角度θ[15]可以表示为
θ=atan2[w(uq×νq),uq·νq]
(9)
式(9)中:uq和νq分别为向量u和ν在w的法平面的投影。

图1 第1类Paden-Kahan子问题Fig.1 The subproblems of the first kind Paden-Kahan
2 6R机械臂逆运动学
2.1 运动学建模
机械臂结构参数和旋量坐标系如图2所示。从图2可以看出,该机械臂具有6个自由度,且均为转动关节,其中关节2、3、4互相平行,这种构型满足 Piper 准则,所以该机械臂逆运动学具有封闭形式解。
从图2中可以得出各关节方向向量wi和点坐标qi分别为

坐标系s和坐标系b分别为机械臂的基坐标系和末端执行器坐标系;S1~S6为各转动关节的运动旋量;q0为基坐标系s的原点;q1~q6为各关节旋量上一点,其中点q1、q4和q5分别在S1与S2交点、S4与S5交点、S5与S6交点处,点q6位于坐标系b原点处;W1、W2、L1、L2、H1、H2为上述各相邻点之间距离;xs、ys、zs为坐标系s的方向向量;xb、yb、zb为坐标系b的方向向量图2 机械臂的结构参数和旋量坐标系Fig.2 The configuration parameters and screw coordinate system of the manipulator
(10)
(11)
那么vi可以根据式(2)计算得
(12)
为了后文对点qi进行位置变换,定义其次坐标形式为
(13)
最后末端执行器初始位姿M和根据式(1)计算的Si为
(14)
(15)
根据式(4),图2中的六自由度串联式机械臂的正运动学可以表示为
Te(Θ)=e[S1]θ1e[S2]θ2e[S3]θ3e[S4]θ4e[S5]θ5e[S6]θ6M
(16)
有了机械臂运动学参数就可以应用旋量理论与代数相结合的方法求解上述构型机械臂的逆运动学。
2.2 求解θ1
在式(16)的左右两侧同时右乘M-1可得
(17)

(18)
式(18)等号右侧均为已知量,为了便于后续推导,设
(19)

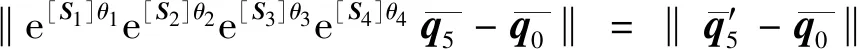
(20)

(21)
设
(22)
有
(23)
解得
(24)
将式(22)和式(19)代入式(18)得
(25)
θ1=atan2[w1(up1×νp1),up1νp1]
(26)
式(26)中:
(27)
2.3 求解θ5和θ6
因为运动旋量S2、S3和S4相互平行,所以这3个运动旋量对于姿态的影响可以看做一个整体,即θ234=θ2+θ3+θ4。由图2可知,运动旋量S2~S6带来的姿态变化可以等效为Y-Z-Y欧拉角变换
(28)
式(28)中:c234=cosθ234,s234=sinθ234,c5=cosθ5,s5=sinθ5,c6=cosθ6,s6=sinθ6。该Y-Z-Y欧拉角变换Ryzy可以根据已知参数计算,将式(17)左乘e-[S1]θ1得
e[S2]θ2e[S3]θ3e[S4]θ4e[S5]θ5e[S6]θ6=e-[S1]θ1Ta=
(29)
这里采用式(28)和式(29)对应元素相等的代数方法求解θ5和θ6。根据式(28)第2行第2列元素对应相等可以求得θ5,即
θ5=±arccos[Tb(2,2)]
(30)
根据式(28)第2行第1列和第2行第3列元素对应相等可以求得
(31)
(32)
那么θ6可以被计算为
1977年起,他参加了国内外举办的400多场团体展览,获得了150多个奖项。至今布兰尼斯拉夫布尔基在国内外已经举办了31场个人影展。在国际摄影艺术联合会,他拥有MFIAP、HonEFIAP、EFIAP、EFIAP/Silver等荣誉。在塞尔维亚摄影协会,他享有摄影大师的最高艺术头衔。自2003年以来,他一直担任塞尔维亚摄影协会主席。
θ6=±atan2(s6,c6)
(33)
由于θ5和θ6已知,那么根据式(28)第1行第1列和第1行第3列元素对应相等可以求得
s234=Tb(1,3)c6-Tb(1,1)s6
(34)
根据式(28)第3 行第1 列和第3 行第3 列元素对应相等可以求得
c234=Tb(3,3)c6-Tb(3,1)s6
(35)
所以θ234可以被计算为
θ234=±atan2(s234,c234)
(36)
2.4 求解θ2、θ3和θ4
式(29)右乘e-[S6]θ6e-[S5]θ5得
e[S2]θ2e[S3]θ3e[S4]θ4=Tbe-[S6]θ6e-[S5]θ5=Tc
(37)

(38)
因为S2与S3互相平行,点q4的轨迹投影图如图3所示。图中点O2和O3分别为点q2和q3,α、β、θ′2、θ′3分别为各向量间的夹角。向量uq、vq、O32和O23可表示为
(39)

图3 轨迹投影图Fig.3 The trajectory projection
根据第1类Paden-Kahan子问题的求解公式计算θ′3和θ′2得
θ′3=atan2[w3(uq×O32),uqO32]
(40)
θ′2=atan2[w2(O23×vq),O23vq]
(41)
根据三角形余弦定理,角度α和β可以表示为
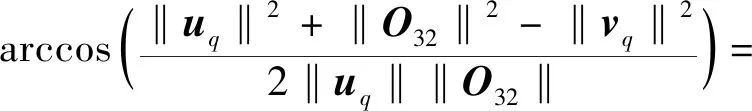
(42)

(43)
有了上述参数,θ2和θ3可以计算为
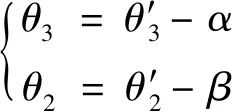
(44)
最后,θ4可以被表示为
θ4=θ234-θ3-θ2
(45)
3 实例与验证
UR5协作机械臂满足所述机器人的构型要求,为了验证提出的逆运动学求解算法的正确性,将该机械臂作为实例进行逆运动学求解。UR5机械臂各结构参数的数值是W1=0.109 m,W2=0.082 m,L1=0.425 m,L2=0.392 m,H1=0.089 m,H2=0.095 m。具体过程如下。
(1)任意给定一组关节角度。
(46)
(2)根据正运动学计算公式[式(16)]计算的末端执行器位姿如式(47)所示。
(3)由逆运动学计算公式可以求出逆运动学的8组解,如表1所示,该8组解的位姿如图4所示。
(4)步骤(3)中8组逆解的位姿与步骤(2)中的位姿作差得出误差矩阵并计算该矩阵的2范数。通过计算,第7组解对应的位姿误差矩阵的2范数最大,为1.072 782 134 37×10-15,该位姿误差矩阵ΔTmax如式(48)所示。

(47)

表1 逆运动学求解的8 组解Table 1 The 8 groups of solutions for inverse kinematics

图4 逆运动学求解的8组解的位姿Fig.4 The poses of 8 sets of solutions solved by inverse kinematics
ΔTmax=Te-Te7≈
(48)
式(48)中:Te7为步骤(3)中第7组逆解对应的位姿。
(5)为了更进一步说明提出算法的鲁棒性和准确性,将步骤(1)~步骤(4)循环执行1 000次,然后对1 000组ΔTmax取平均,计算结果为
(49)
4 结论
(1)利用旋量理论与代数相结合的方法推导了六自由度且具有相互平行的3个相邻关节轴的串联式机械臂的逆运动学求解公式,该方法具有几何意义明确的优点,并以UR5型号机械臂为例进行逆运动学求解,计算得出逆解的最大位姿误差为10-15数量级,与文献[9]相比,其最大位姿误差为10-12数量级,因此,该精度足以验证算法的准确性和优越性。
(2)提出的逆运动学求解算法针对一类具有相互平行的3个相邻关节轴构型的机械臂,该构型常见于协作式机器人。因此,提出的逆运动学算法具有一定通用性。
