车致桥梁振动与黏滞阻尼器参数

2021-09-26陈永祁郑成成郑久建马良喆

科学技术与工程 2021年25期

陈永祁，郑成成，郑久建，马良喆

(1.北京奇太振控科技发展有限公司，北京 100037；2.燕山大学建筑工程与力学学院,秦皇岛 066004)

大跨度桥梁为减小结构的内力响应，常采用纵向无约束的隔震体系，但也由此带来了车辆荷载作用下桥梁结构较为强烈的振动问题。中外的一些学者针对此类问题进行了相关研究。Xiao等[1]研究了美国阿拉斯加州丘利塔河大桥在移动车辆荷载作用下的非线性动力特性；Yin等[2]研究了冲击调谐质量阻尼器对移动车辆荷载引起的桥梁结构动力响应的抑制作用；Li等[3]利用自行开发的车桥耦合振动分析程序，研究了加宽桥梁在各种车辆荷载作用下的动力响应；刘安胜等[4]采用数值模拟的方法研究了移动行车荷载对拱桥耐久性的影响；高庆飞等[5]通过理论分析与数值模拟结合的方式，研究了移动车辆荷载作用对桥梁冲击系数的影响；顾颖等[6]通过数值模拟的方式，研究了不同车速下高低塔斜拉桥主梁跨中位置的动挠度、冲击系数及竖向加速度等动力时程响应的变化情况；朱劲松等[7]利用裂缝尖端三维动态应力强度因子求解法，分析了梁体裂缝在移动车辆荷载激励下的扩展规律；Liu等[8]通过建立有限元模型，对车辆在路面系统上的移动负荷进行了模拟，详细分析了各参数的动态响应情况。综上可以看出，现有研究主要以车桥耦合分析模型的建立及结构动力响应分析等为主，对于了解车桥耦合相互作用的机理及车辆荷载对桥梁结构耐久性、冲击系数、裂缝扩展的影响有很大帮助，但对车辆荷载引起的桥梁振动控制的研究较少。

随着中国公路桥梁抗震设计理念的不断演变，其设计理念和方法已由单一依据强度验算逐渐修改为依据强度和变形双重指标控制的抗震设计[9]。黏滞阻尼器凭借着对主梁位移及墩底内力良好的控制效果在桥梁工程中得到了广泛应用[10-11]。而与强烈的地震响应相比，车辆荷载引起的结构振动相对较小，因此目前关于黏滞阻尼器的应用研究仍主要在桥梁的抗震领域，阻尼器参数的选用也主要依据地震响应分析的结果。但随着车流量的增加和行车速度的增大，高频次车辆荷载引起的振动问题已严重影响到大跨度桥梁结构的耐久性和行车的舒适性。当初仅针对桥梁抗震要求选用的黏滞阻尼器，其参数设计由于缺乏对车辆荷载作用的考虑，在长期的被动工作中容易提前发生疲劳破坏，造成结构保护的失效[12-13]。例如，中国的江阴长江大桥在车辆荷载作用下的梁端位移平均日累计量达到了93.36 m，使大桥伸缩缝仅工作4年且远未达到其40年的使用标准和最大允许行程的情况下就发生了破坏，同时支座也有损坏[14-15]。类似的情况在宜昌长江公路大桥和润扬长江大桥南汊桥上也有出现。可见，因对车辆荷载作用的重视不足而造成的大跨度悬索桥结构的疲劳破坏已成为亟待解决的问题之一。

基于以上原因，为更好地应对日常高频次车辆荷载对悬索桥的扰动作用，提高黏滞阻尼器抵抗疲劳破坏的能力，现以宜昌长江公路大桥为依托工程，通过建立大桥的有限元模型，对车辆过桥的整个动力过程进行模拟分析，并对设置黏滞阻尼器前后的时程响应进行比较计算，研究阻尼器参数变化对悬索桥振动控制的影响。

1 有限元模型建立及动力特性分析

1.1 工程概况

宜昌长江公路大桥(图1)采用双塔单跨布置，全桥跨径分布为(246.25+960+246.25)m，垂跨比为1/10，主缆横向间距24.4 m。全桥吊索共156根，桥塔侧的吊索距桥塔中心线的纵向距离为15.69 m，其他吊索纵向间距为12.06 m。主梁采用扁平钢箱梁，其梁全宽30 m，梁高3 m，为双向四车道设计。本桥结构设计采用全漂浮体系，跨中未设中央扣，总体布置如图2所示。

图1 宜昌长江公路大桥Fig.1 Yichang Yangtze River Bridge

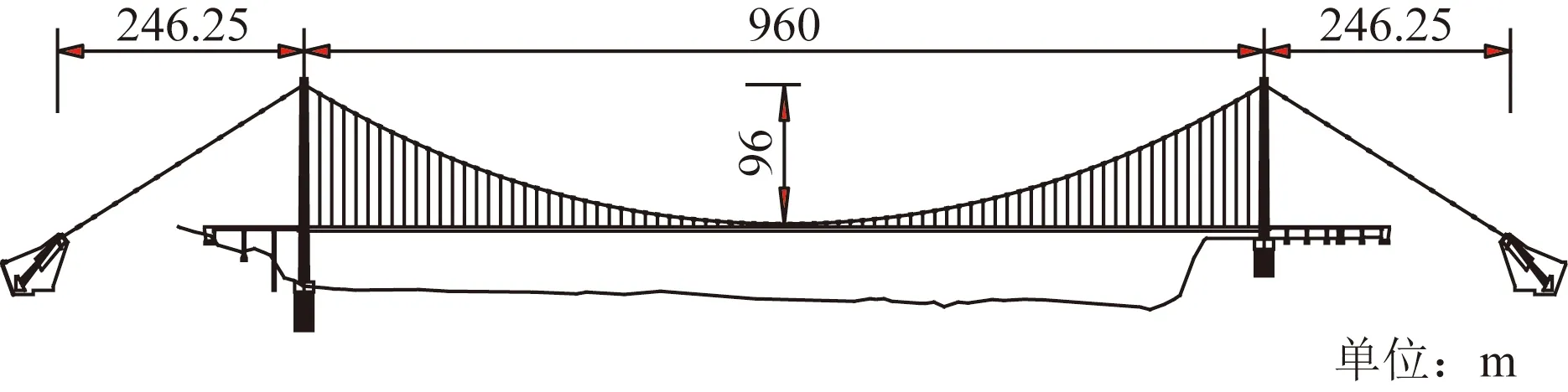
图2 悬索桥总体布置图Fig.2 General arrangement diagram of suspension bridge

1.2 有限元模型

基于Sap2000有限元软件建立悬索桥的计算模型。主梁、桥塔及横梁采用梁单元模拟，其中主梁采用鱼骨刺单梁形式；主缆和吊索采用索单元模拟，并考虑成桥索力产生的初始刚度矩阵；桥面系二期恒载及主缆、吊索的附属材料和设施，均以质量形式考虑，不计其对刚度的影响；黏滞阻尼器使用Maxwell模型的Damper连接单元模拟。全桥共有946个梁单元、320个索单元和计算采用的8个阻尼器连接单元。边界条件：塔底固结，边缆锚锭处铰接，主梁梁端竖向与横向平动自由度与桥塔横梁采用主从约束连接，其他自由度释放，形成纵飘体系。全桥有限元模型如图3所示。

图3 悬索桥有限元模型Fig.3 Finite element modal of suspension bridge

1.3 动力特性分析

采用飘浮体系结构的大跨度悬索桥具有明显的几何非线性，即P-Δ效应和大位移，其中，P-Δ效应也称侧移效应，因杆件-端节点偏差而产生。在进行动力时程分析时需提供实际成桥的初始状态，包括初始刚度、内力和位移。故在动力时程分析前，需先进行成桥恒载下的非线性静力分析，在分析中考虑缆索体系的几何非线性，并保存最终结果作为后续分析的初始状态。表1给出了该悬索桥的自振特性。

表1 悬索桥自振特性Table 1 Natural vibration characteristics of suspension bridge

从表1可以看出，第1、3阶悬索桥的振动特性呈现出纵飘振动与竖向振动相互耦合的特点。众多桥例的分析结果反映出悬索桥振动耦合效应主要表现为主梁纵飘与低阶反对称竖向挠曲振型的耦合，以及侧向弯曲与扭转振型的耦合，尤以前者更为明显[16]。因此，悬索桥在车辆荷载作用下激起竖向振动的同时势必引起结构的纵向振动，后续的分析结果也验证了这点。

2 车致桥梁的纵向振动

该悬索桥由于采用了全飘浮体系，自振周期很长，使载重汽车1.5～4.5 Hz的固有频率远高于其主要的竖向自振频率[17]。考虑到车辆的质量远小于桥的质量，车辆自振对车桥耦合振动的影响也很小，因此车辆过桥的动力作用可以用移动荷载来模拟[18-19]。

根据《公路桥涵设计通用规范》(JTG D60─2015)[20]，选用公路-Ⅰ级车辆荷载模型，车速为V，前后车之间的距离为s，并由n辆车组成一列车队。每辆车的自重用5个集中力模拟，具体荷载布置情况如图4所示。

图4 移动车辆荷载布置Fig.4 Layout of moving vehicle loads

为研究车辆荷载作用下大跨度悬索桥的纵向振动特性，分别对单向车队过桥和双向车队过桥两种工况进行非线性时程分析，并考虑不同车速V和车距s对结构动力响应的影响。

2.1 单向车队过桥

单向车队过桥采用在一侧车道以速度V匀速行驶的单列车队进行模拟，n取9，s保持一定。考虑车距s分别取40、60、80和100 m，车速V分别取20、30、40、50、60、70、80、90、100 km/h，计算不同车距s和车速V组合下的所有工况，共36个。提取悬索桥结构主要部位处的竖向和纵向位移的计算结果，s=40 m,V=80 km/h的计算结果如图5(a)、图6(a)、图7(a)所示。其中主缆垂点为主缆跨中最低点，所绘竖向位移分别为主梁1/8、1/4、3/8和1/2跨处位置的位移，后文所述亦同。

2.2 双向车队过桥

在进行双向车队过桥分析时，采用速度相同的两列车队沿两侧车道相向行驶，模拟从开始入桥到刚离开的整个过程。n取9，s保持一定。s分别取40、60、80和100 m，车速V分别取20、30、40、50、60、70、80、90、100 km/h，计算不同车距s和车速V所有组合下的工况，共36个。计算结果如图5(b)、图6(b)、图7(b)所示。

2.3 结果分析

从图5和图6可以看出，无论车队以何种形式过桥，车辆荷载在引起悬索桥竖向振动的同时，均会引起较大的纵向振动。在单向车队和双向车队过桥时，主梁及其他各部位的竖向振动和纵向振动时程曲线以车队到达跨中的时间点(约30 s处)为对称中心分别呈现出近似反对称和正对称的特征。

比较图7(a)和图7(b)可知，在不同的车距和车速下，一列车队单向过桥均比两列车队双向过桥引起的主梁纵向位移大。分析其主要原因是：单向车队过桥和双向车队过桥的过程，在每个时间点上主梁车辆荷载分布分别相当于反对称和正对称竖向布载，前者主要激起结构的反对称竖向挠曲振型，后者主要激起正对称竖向挠曲振型。而由悬索桥第一阶自振特性可知，其振动耦合效应主要表现在纵飘振动与反对称竖向挠曲振型的耦合，因此单车队过桥引起的主梁纵向振动相对更大。且可以发现，当s=40 m、V=80 km/h时，无论车队以何种形式过桥，主梁的纵向振动响应都较大，并随车距s的增大而减小，而车速V对其影响较小。

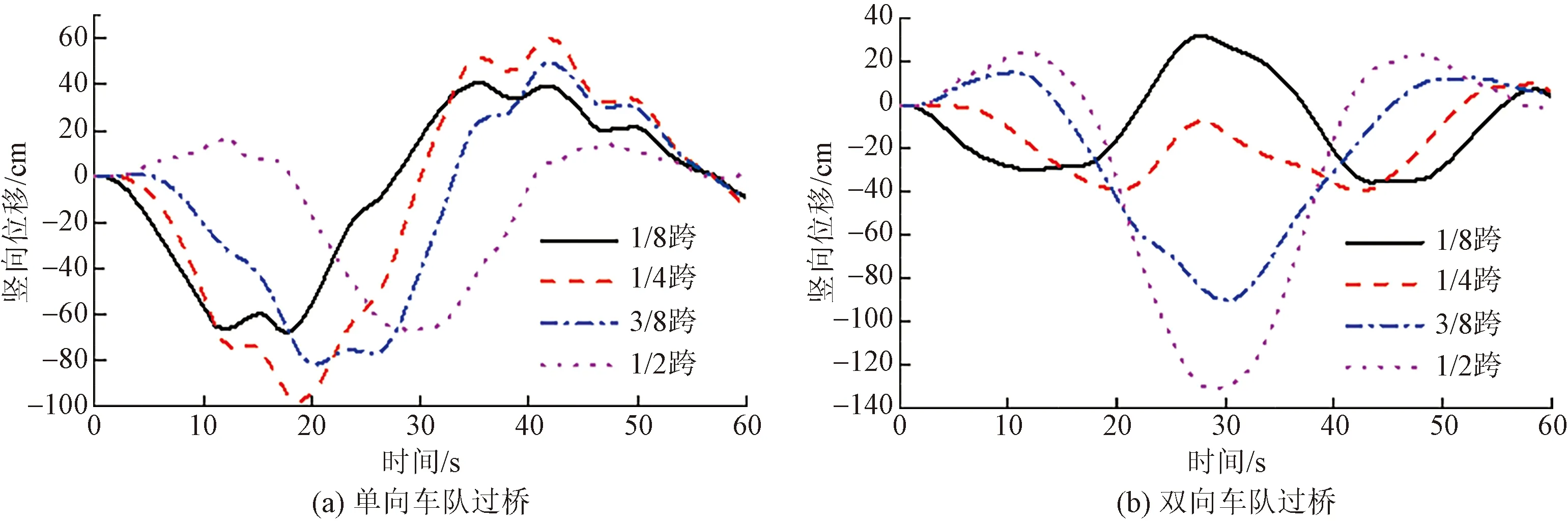
图5 主梁竖向位移时程Fig.5 Vertical displacement time history of main beam

图6 不同结构位置的纵向位移时程Fig.6 Longitudinal displacement time histories of different structural locations

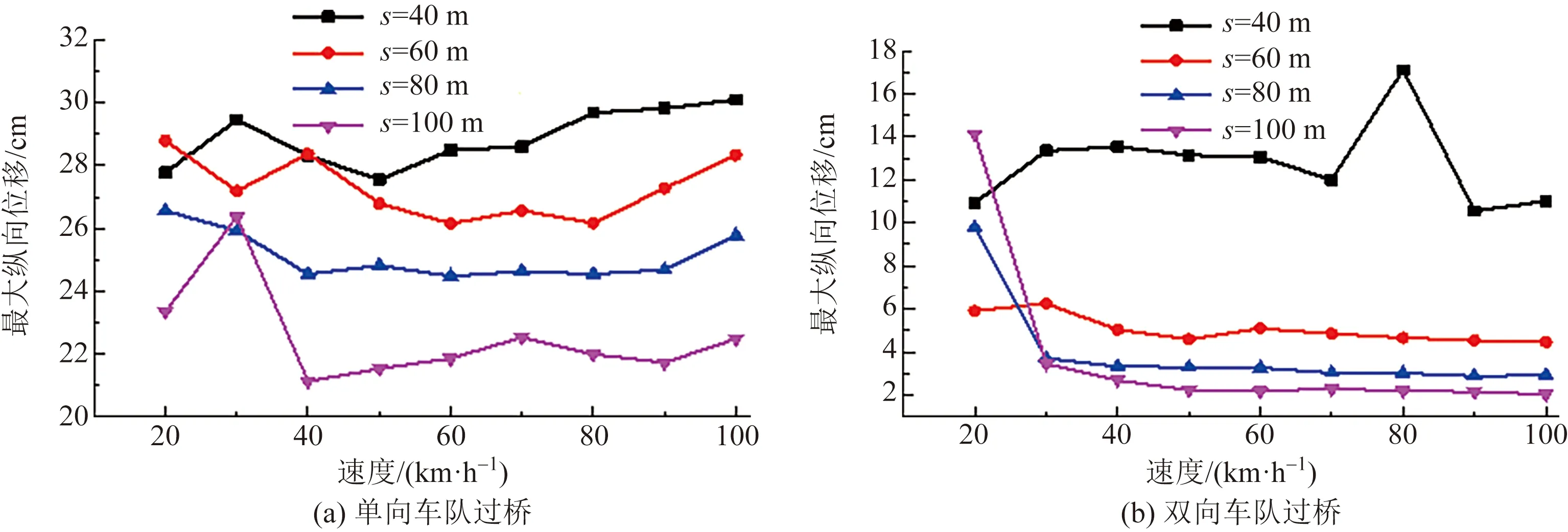
图7 梁端最大纵向位移Fig.7 Maximum longitudinal displacement of beam end

3 车辆荷载作用下黏滞阻尼器参数研究

3.1 黏滞阻尼器的工作原理

目前，在桥梁减振领域广泛应用的黏滞阻尼器，属于速度相关型减振装置，主要组成部分为缸体、阻尼介质、带小孔的活塞、活塞杆以及密封件等。在车辆荷载作用下，活塞杆牵动活塞在缸体内往复运动并产生阻尼力。阻尼力[10]的表达式为

F=CVα

(1)

式(1)中：F为阻尼力；C为阻尼系数；V为阻尼器连接两端的相对速度；α为速度指数(取值范围在0.2～2.0，常用取值一般在0.2～1.0)。阻尼器的滞回曲线如图8所示。

3.2 黏滞阻尼器参数敏感性分析

阻尼器一般设置在悬索桥振动相对位移较大的塔-梁连接处或主梁端部，选取在每侧塔-梁连接处各设置4个纵向阻尼器，全桥共8个。考虑到该桥为双向四车道设计，因此分别在单向两车道和双向四车道两种行车工况下进行计算。假设每列车队车辆数n=9，车辆间距s=40 m、车速V=80 km/h，且各列车队同时进出桥梁。

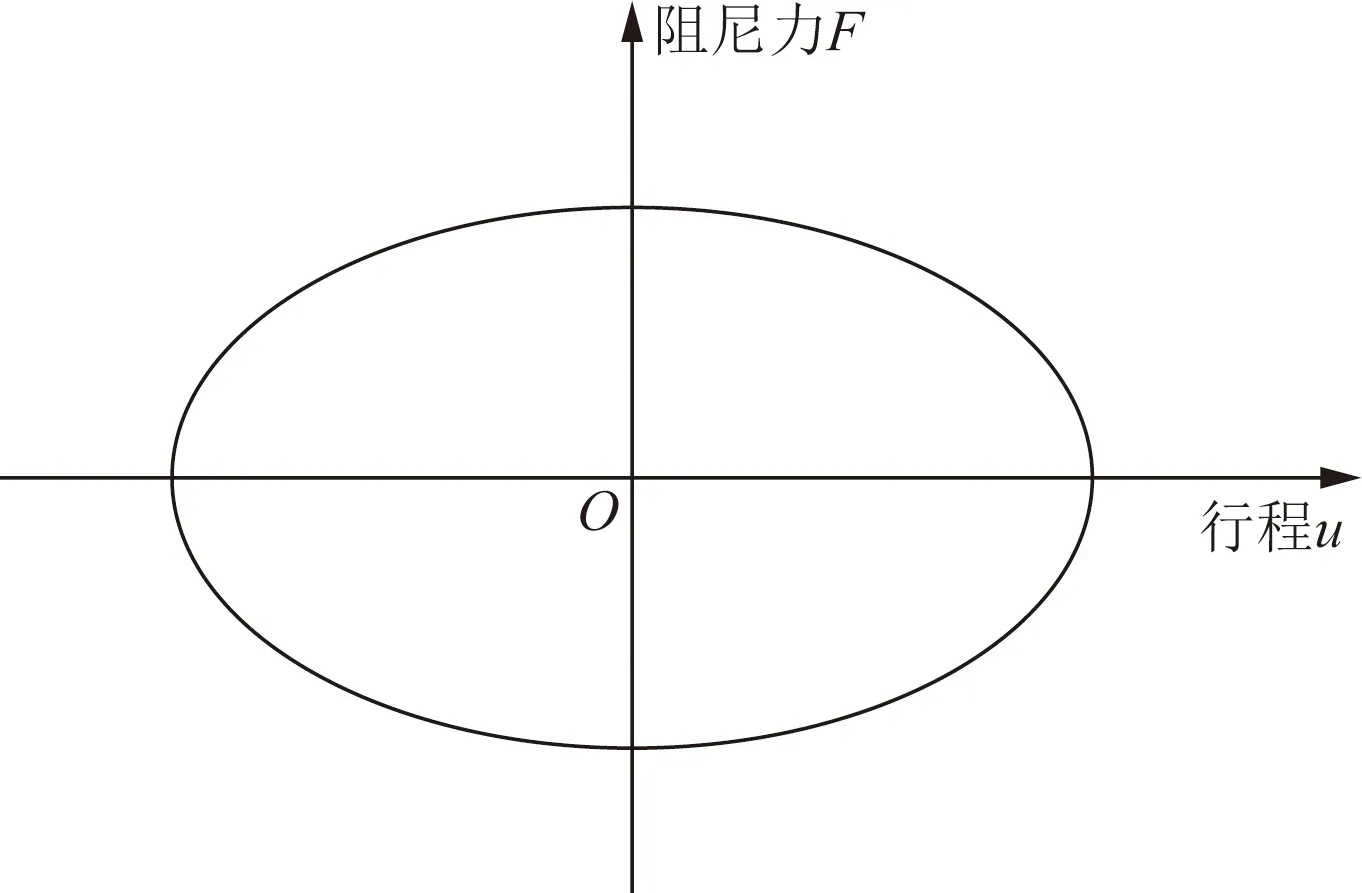
图8 阻尼器的滞回曲线Fig.8 Hysteresis curve of damper

由式(1)可知，选取不同的速度指数α、阻尼系数C，阻尼器会表现出不同的性能，将会对结构的动力响应产生不同的影响。为了将悬索桥在车辆荷载下的动力响应控制到最优，需先进行阻尼器参数的选取。为此，速度指数α分别取值为0.3、0.5、0.7和1.0，阻尼系数C分别取值范围为500～5 000 kN·s/m，取值间距500 kN·s/m，即总的阻尼系数CT(CT为全桥8个阻尼器的阻尼系数之和)取值范围为4 000～40 000 kN·s/m。分别计算无阻尼器和设置不同参数阻尼器的悬索桥在车辆荷载作用下的振动响应。结构关键部位响应的最大绝对值随阻尼器参数的变化情况如图9～图12所示。其中梁端最大位移为梁端纵向绝对值最大位移；梁端累计位移为梁端在车队上桥到离开的整个过程中的纵向累计位移。

从图9～图11可以看出，阻尼器选取合适的参数不仅可以显著减小单向、双向车队过桥引起的主梁纵向位移和累计位移，最大减振率均在90%以上，还可以减小主梁的竖向振动位移，最大减振率为22%。主梁梁端最大位移、梁端累计位移和1/4跨处的竖向最大位移随阻尼器参数变化的规律为随速度指数α的增加而变大，随着阻尼系数C的增加而变小[21]。说明在单向、双向车队过桥下振动响应具有一致性，即阻尼器参数的变化对三者的控制具有一致的影响效果。

图9 梁端最大位移随阻尼器参数变化Fig.9 The maximum displacement of the beam end varies with the damper parameters

图10 梁端累计位移随阻尼器参数变化Fig.10 Cumulative displacement of beam end varies with damper parameters

图11 主梁1/4跨处最大竖向位移随阻尼器参数变化Fig.11 The maximum vertical displacement at the 1/4 span of the main beam varies with damper parameters

图12 最大阻尼力随阻尼器参数变化Fig.12 The maximum damping force varies with damper parameters

现以梁端最大响应位移为例，进行详细说明。从图9可以看出，当C一定时，梁端最大位移随α的增大而增大；当α一定时，梁端最大位移基本随C的增大而减小，当C增大到一定值时，位移衰减趋于平缓。在参数α和C相同时，双向车队过桥时阻尼器对梁端位移的控制效果在77%～94%，明显优于对单向车队过桥控制效果的15%～91%，且在α=0.3时对两种行车工况的控制效果均较好。以控制主梁纵向振动位移为优化目标，综合考虑单向、双向车队过桥，阻尼器参数倾向于α取小值、C取大值。综合考虑阻尼器参数取值过大带来的安装困难及经济性，当α取0.3，C取4 000 kN·s/m(即CT取32 000 kN·s·m)时，对主梁纵向振动位移控制效果较好。

从图12可以看出，在所有工况下，阻尼器最大力均未超过1 000 kN，即全桥8个阻尼器的合力未超过8 000 kN，说明阻尼器在车辆荷载作用下出力较小，远在其安全工作范围内。由于大跨度桥梁黏滞阻尼器选用的主要目的仍是针对地震作用，因此为进一步确定具有足够安全储备的阻尼器参数，需在车辆荷载分析的基础上再进行地震响应分析。现主要针对车辆荷载下的阻尼器参数研究，不对地震响应做过多分析。

4 悬索桥黏滞阻尼器参数的选用

对于桥梁抗震用黏滞阻尼器的选用，通常只需考虑阻尼力、冲程、速度指数和阻尼系数等参数的影响。但对于既要承担抗震任务又要对车辆荷载起控制作用的阻尼器除考虑以上参数外，还须考虑在车辆动荷载下的累计行程和工作功率(输出功率)。通过这两个参数分别来衡量阻尼器的累计磨损量和单位时间耗能的大小。阻尼器的累计行程可以用塔-梁相对位移的累计量来代替，由于塔-梁相交处塔的纵向位移在车辆荷载作用下很小，相对主梁的位移可以忽略，所以阻尼器的累计行程与主梁梁端累计位移等同。因此，对阻尼器参数的优化选取与前文对梁端最大位移的控制有相同之处。

车辆荷载作用下的阻尼器的工作功率计算式为

P=W/t

(2)

式(2)中：P为阻尼器的工作功率；W为车队过桥时阻尼器的滞回耗能；t为车队过桥的时间。

通过分析发现，阻尼器在单向车队过桥时的工作功率比在双向车队过桥时大，故以单向车队过桥时阻尼器的工作功率作为控制目标。阻尼器在不同参数下的工作功率如图13所示。

由图13可知，随着阻尼系数C的增大，速度指数α越小，阻尼器工作功率降低的速率越快。当α取0.3，C取4 000 kN·s/m(即CT取32 000 kN·s/m)时对工作功率的控制效果较好。

车辆荷载作为一种日常动力荷载几乎作用于悬索桥的整个生命周期，使黏滞阻尼器工作的次数远大于地震。因此，用于桥梁抗震选用的阻尼器无法避免且将长期经受这种高频次疲劳荷载的作用，这对阻尼器是一种巨大的工作负担。因此，在进行悬索桥阻尼器参数设计和选用时，应先以车辆荷载作用下的主梁纵向位移、阻尼器的累计行程和工作功率作为优化计算的控制目标，确定一个初步的参数范围。然后在此参数范围内，根据地震响应分析的计算结果，来确定最优的阻尼器参数。由于阻尼器参数的选用是综合考虑了日常车辆荷载和偶然地震荷载的共同作用，所以阻尼器的出力和冲程应为两种作用的叠加值，以保证阻尼器具有足够的安全储备。