基于多变量混合长短期记忆神经网络的长沙PM2.5预报模型

罗 宇，袁 薇，罗林艳，陈明诚，唐 杰，万文龙，范嘉智

(1.中国气象局气象干部培训学院湖南分院，长沙 410125；2.湖南省气象防灾减灾重点实验室，长沙 410118；3.中国气象局气象干部培训学院，北京 100081；4.湖南省气象信息中心，长沙 410118；5.南京信息工程大学大气科学学院，南京 210044；6.湖南省气象台，长沙 410118；7.东营市气象局，东营 257100)

随着工业发展和城市化，空气污染问题已在世界范围内引起广泛关注，世界卫生组织研究[1]指出每年约有超400万人因空气污染相关疾病死亡。长沙作为湖南省会，人口密度大、工业发达，且由于特殊的地理位置，易造成区域型空气污染[2]，仅2019年冬季就出现了4次重污染过程，其首要污染物为PM2.5[3]。PM2.5是指空气动力学当量直径小于等于2.5 μm的颗粒物，可长时间悬浮于空气中，并吸附重金属和挥发性有机物等有毒污染物[4]。相关研究表明，环境中PM2.5浓度每增加10 μg/m3，心脑血管疾病和肺癌的死亡风险增加4%～8%[5-6]。同时，PM2.5能够影响大气的成云致雨过程，间接影响气候变化[7]。

近年来，中外学者针对PM2.5特征及其浓度预报进行了大量研究。总体而言，PM2.5浓度预报方法可分为确定性方法和统计方法两类。确定性方法利用大气科学相关理论对污染物的物理化学反应进行建模，模拟其排放、扩散和传输等过程。目前在城市空气污染预报中使用较多的确定性模型主要有嵌套网格空气质量预报模型[8](nested air quality prediction model，NAQP)，气象-化学耦合模型[9](weather research and forecasting model coupled to chemistry，WRF-Chem)和多尺度空气质量模型[10](community multiscale air quality model，CMAQ)。这些模型均基于一定的理论假设和先验知识构建，因此有助于更好地理解大气污染机理，但在模型输入条件准确性、物理化学过程描述和计算有效性提升等方面仍面临较大挑战[11-12]。统计方法则直接利用统计模型找出不同变量与PM2.5之间的关系，并将这一关系应用到空气质量预报中。张天航等[13]采用多元线性回归集成方法，较大幅度降低了空气质量数值预报偏差；杨正理等[14]构建基于随机森林的城市空气质量预测模型，可较好改进大数据背景下的预测精度；杨涛峰等[15]结合自回归积分滑动平均(autoregressive integrated moving average，ARIMA)和支持向量机(support vector machine，SVM)对北京某站点PM2.5浓度进行预测，取得了良好的预测精度；张岳军等[16]基于华北区域环境气象数值预报系统预报结果，利用后向传播神经网络建立10 d的滚动修正模型对太原市空气质量预报进行修正。20世纪80年代出现的循环神经网络(recurrent neural network，RNN)，能对序列数据的非线性特征进行高效率学习，而作为RNN变体之一的长短期记忆(long short-term memory，LSTM)因可有效解决简单RNN的梯度爆炸或消失问题，使其在空气污染预报方面展现出广泛的应用前景。白盛楠等[17]和Li等[18]基于LSTM构建预测模型对北京市PM2.5浓度分别进行逐日和逐小时预测，发现LSTM神经网络可较好提取PM2.5浓度时序特征，在不同的时间分辨率上均取得较好的预报精度。

在分析长沙各空气质量监测站PM2.5浓度的时空相关性基础上，现提出一种基于LSTM的多变量混合PM2.5逐小时预报模型，对长沙10个空气质量监测站PM2.5浓度进行逐小时预报，为PM2.5统计预报模型提供新的思路。

1 资料与方法

1.1 资料选取

本研究使用数据时间段为2014年5月13日—2020年8月30日，其中空气质量数据为长沙10个空气质量监测站探测得到的逐小时数据，由中国环境监测总站全国城市空气质量实时发布平台获取，包含颗粒物(PM10、PM2.5)、二氧化硫(SO2)、二氧化氮(NO2)、一氧化碳(CO)、臭氧(O3)和空气质量指数(AQI)；对应时段的气象数据使用长沙市黄花国家基本气象站探测得到的小时数据，包含气压(P)、气温(T)、相对湿度(RH)、能见度(VIS)、风向(WD)和风速(WS)，由全国综合气象信息共享平台(CIMISS)获取。研究涉及站点位置分布和基本信息如图1所示，其中黄花站为气象站，其他为空气质量监测站。对于少量缺测数据，利用R语言imputeTS包的卡尔曼平滑(Kalman smoothing)算法进行插补。

1.2 PM2.5数据时空相关性分析

计算长沙市10个空气质量监测站PM2.5浓度之间的Pearson相关系数，用以分析各站PM2.5浓度的空间相关性，如表1所示，所有相关系数均在0.88以上，表明各站间的PM2.5浓度具有强相关性，因此考虑利用单一模型对所有监测站的PM2.5浓度进行建模预报。随后，利用自相关函数研究各站PM2.5浓度序列的时间相关性，其计算公式为

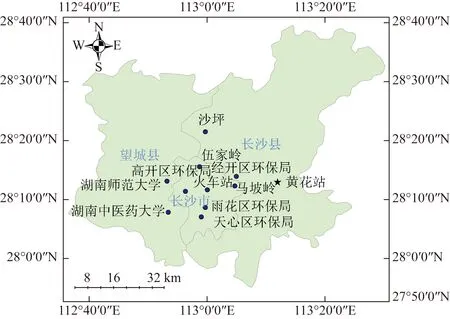
图1 站点位置分布情况Fig.1 Locations of air quality monitoring stations and meteorological station

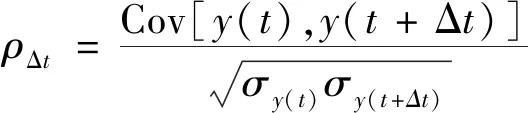
(1)

式(1)中：y(t)和y(t+Δt)分别为t和t+Δt时刻的PM2.5浓度；Cov(·)和σ(·)分别为PM2.5浓度的协方差和方差。各站PM2.5浓度序列的自相关系数如图2所示，随滞后阶数的增加逐步减小，表明较早的PM2.5浓度对当前值的影响随时间间隔的增大逐渐降低；同时还可以发现当时间间隔小于24 h时，各站PM2.5浓度的自相关系数均大于0.6，因此可将预报模型的最佳时间窗选择范围缩小到24 h以内。

1.3 多变量混合LSTM模型

LSTM是由Hochreiter等提出的一种改进的循环神经网络(RNN)[19]，依靠内部特殊的自连接设计，可以提取任意长度时间序列的自回归结构，目前广泛应用于文本生成[20-21]、语音识别[22-24]、机器翻译[25]、气象及环保[17-18,26-28]等领域。LSTM单元结构如图3所示，其对应计算公式如式(2)～式(6)所示。

it=σ(Wxixt+Whiht-1+bi)

(2)

ot=σ(Wxoxt+Whoht-1+bo)

(3)

ft=σ(Wxfxt+Whfht-1+bf)

(4)

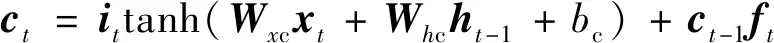
(5)

图2 各站PM2.5浓度自相关系数Fig.2 Autocorrelation coefficients of PM2.5 concentrations in stations

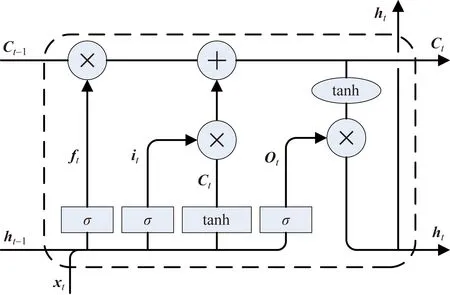
it、ot和ft分别为输入门、输出门和遗忘门3个门控结构，分别控制输入、输出和保留在LSTM单元内信息的多少；ct为单元间激活向量；ht为存储了t时刻及之前时刻有用信息的隐状态向量；xt为t时刻输入向量；σ(·)为sigmoid函数；tanh(·)为激活函数图3 LSTM单元结构Fig.3 Structure of LSTM cell

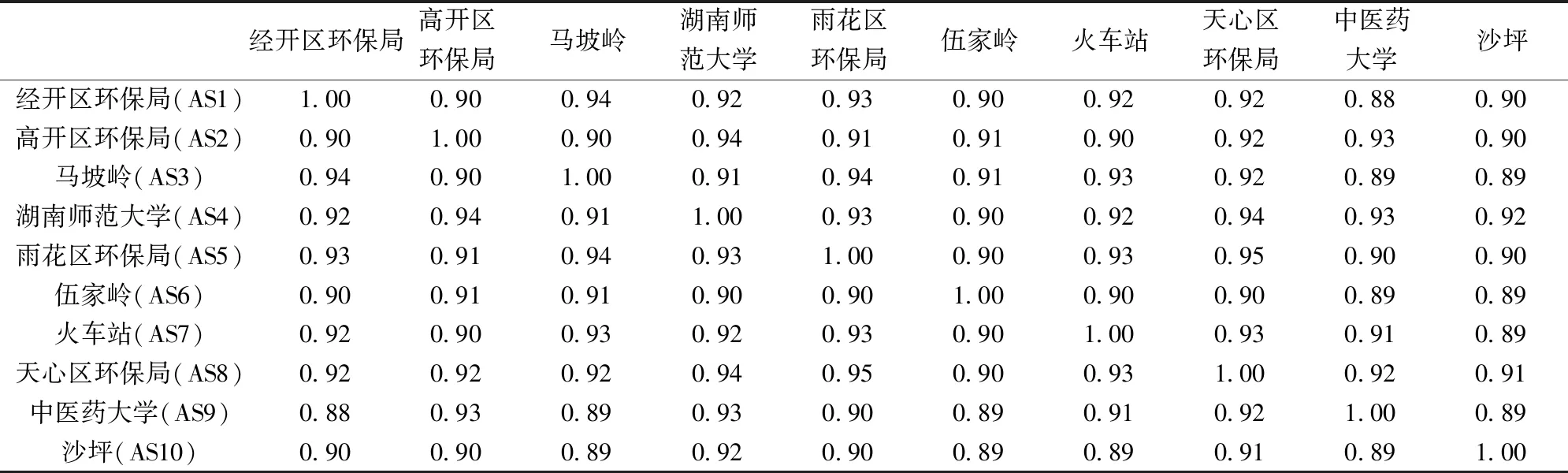
表1 各站PM2.5浓度相关系数Table 1 Correlation coefficients of PM2.5 concentration between stations

ht=ottanh(ct)

(6)

式中：W为权重矩阵；b为偏置项。σ对应的计算公式为

(7)

提出的多变量混合LSTM(hLSTM)模型利用LSTM层提取空气质量数据和气象数据时序特征，并结合日期时间信息对未来24 h的PM2.5浓度进行逐小时预报，其结构如图4所示。不同大气污染物之间在一定条件下会发生各种物理化学反应[29-30]，加剧大气污染程度；同时大量研究表明[2,31-32]，PM2.5的浓度变化与大气温度、湿度、气压和风速等气象条件存在一定相关性，因此将10站的空气质量数据(PM2.5、PM10、SO2、NO2、CO和O3)以及长沙气象数据(P、T、RH、VIS、WD和WS)组成特征因子张量作为模型LSTM层的输入。除此之外，数据观测时间等附加信息的引入也可在一定程度上提升预测精度[33]，因此通过一位有效编码(one-hot encoding)将PM2.5浓度数据的日期时间信息引入模型，结合LSTM层提取的时序特征，利用全连接层(dense layer)获取10站的PM2.5浓度24 h逐小时预报结果。

为评价hLSTM模型预报精度，选取均方根误差(root mean squared error，RMSE)、平均绝对误差(mean absolute error，MAE)和平均绝对百分比误差(mean absolute percentage error，MAPE)作为指标，对预报值和观测值的偏离程度进行度量，计算公式为

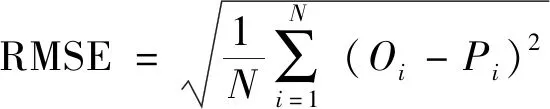
(8)

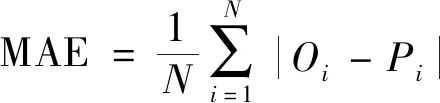
(9)

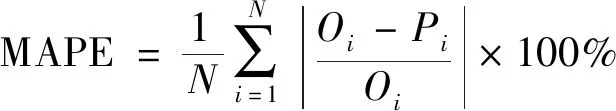
(10)

式中：N为样本数量；Oi和Pi分别为PM2.5浓度观测值和预报值。

1.4 数据预处理

深度学习中，若某些特征因子方差过大，则会主导目标函数从而无法正确地去学习其他特征，造成模型精度降低，甚至无法收敛等问题。因此，本研究采用Standardization标准化方法，将特征因子的分布转换为高斯分布，即均值为0，方差为1。

根据多变量混合LSTM模型结构，由空气质量数据和气象数据组成的原始数据集无法直接作为模型输入，因此利用滚动时间窗方法生成时间序列样本[34]。时间序列样本量N由原始数据量n、时间窗Δt和预报时效h决定，即N=n-(Δt+h)+1。不同大小的时间窗对PM2.5预报精度有直接影响[33-34]，过小的时间窗会造成模型的输入信息不足，而过大的时间窗则可能引入不相关的噪声，且增加计算复杂度。结合1.2节中PM2.5数据自相关分析结果可将Δt范围缩小到24 h内，因此在研究过程中将时间窗分别设置为6、12和24 h，评估其对hLSTM模型预报精度的影响，以选取最适宜的时间窗。除时间窗外，模型中LSTM层数和各层神经节点数也会影响PM2.5预报精度。因此，在确定最适宜时间窗大小的基础上，参考相关研究模型结构[20-22]，选用2层LSTM，各层神经节点数相同，分别设置为50、100和200，评估不同节点数对hLSTM模型预报精度的影响，以确定最适宜的神经网络结构。

图4 多变量混合LSTM模型Fig.4 Multivariable hybrid LSTM model

LSTM层和Dense层激活函数(activation function)分别选用tanh和linear，各层节点丢弃率(dropout rate)设为0.2，以避免过拟合，模型选择均方误差(MSE)作为损失函数(loss function)，采用RMSProp算法作为优化器(optimizer)提升训练效率，参数详细设置如表2所示。研究利用Python和Keras深度学习框架进行。

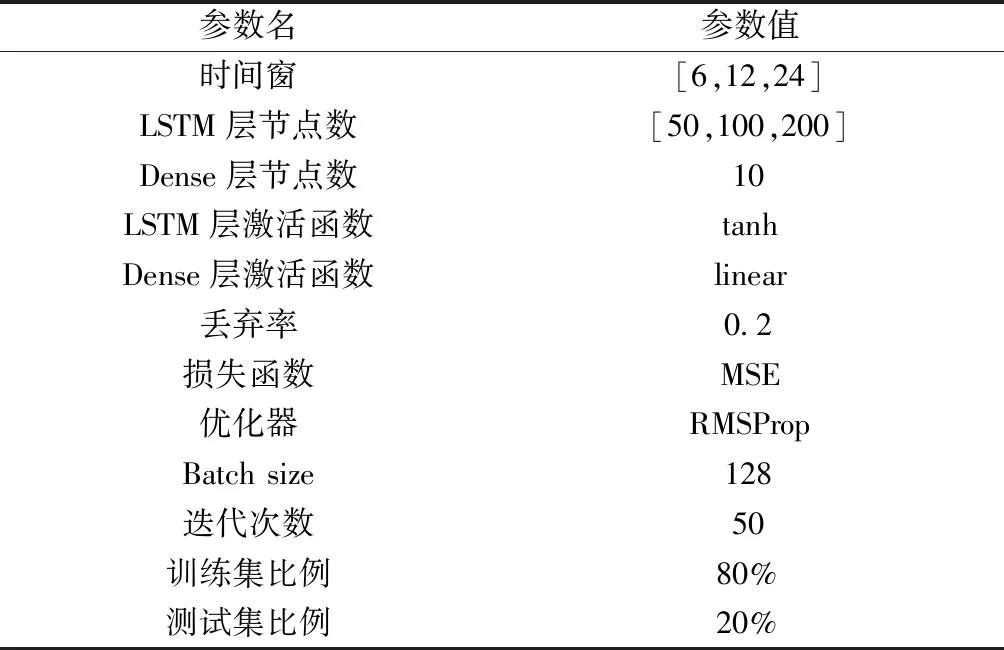
表2 多变量混合LSTM模型参数设置Table 2 Parameter settings of hybrid LSTM model

2 结果与分析

2.1 时间窗和节点数对模型精度影响

为评估时间窗大小和节点数对hLSTM模型预报精度的影响，按照1.4节方案设置时间窗和LSTM层节点数，对长沙10个空气质量站未来24 h的PM2.5浓度进行逐小时预报，利用预报结果绘制箱线图，如图5所示。由图5可知，hLSTM模型的预报误差随时间窗的增大和节点数的增多呈现逐渐增大，6 h时间窗配合50节点数的设置使模型的均方根误差、平均绝对误差和平均绝对百分比误差3项指标均达到最低，且波动均相对较小，对应逐小时均值分别为18.71 μg/m3、12.50 μg/m3和38.95%。产生这一结果原因可能有两个，一是较大的时间窗引入更多不相关数据，使模型训练效率降低，在同样的迭代次数下无法更好提取有效的特征信息；二是较多的神经节点使模型在训练过程中更容易出现过拟合现象，影响模型的泛化能力。因此，选取6 h和50分别作为模型的时间窗和LSTM层节点数。

2.2 预报模型精度

确定最适宜时间窗和LSTM层节点数后，基于训练集数据对hLSTM模型进行训练，并利用测试集数据对10站的PM2.5浓度逐小时预报精度进行验证，结果如图6所示，hLSTM模型误差随PM2.5预报时效的增大，总体呈现逐步增大趋势，10 h前误差增大迅速，10 h后误差增大较为平缓，且呈现震荡性。均方根误差、平均绝对误差和平均绝对百分比误差分别从1 h的6.53 μg/m3、4.03 μg/m3和16.02%增大到24 h的20.62 μg/m3、13.56 μg/m3和47.34%。为对比hLSTM模型和其他机器学习模型的预报精度，引入决策树(DTs)、RNN和普通LSTM作为对比模型，其中RNN模型将hLSTM模型中的LSTM层替换为RNN层得到，普通LSTM模型为hLSTM模型去除附加信息得到，其余参数不变，对比结果如表3所示，作为传统机器学习方法的DTs模型预报误差较基于神经网络的RNN、LSTM和hLSTM模型大，其主要原因是由于后3种模型是专门针对时间序列数据设计的，可以更好地提取数据在时序上的特征；与RNN和普通LSTM模型相比，hLSTM模型的RMSE分别降低6.26%和8.92%，MAE分别降低8.22%和10.91%，MAPE分别降低24.79%和27.99%，表明LSTM层和附加信息的引入可以更好地提取长沙PM2.5浓度时序特征，实现更好的预报效果。同时，hLSTM模型在不同地区均有较好的适用性。采用相同的数据预处理方法和hLSTM模型结构，对湖南省岳阳、常德和衡阳3地PM2.5浓度进行预报，预报精度与长沙基本一致(图7)，均方根误差分别由1 h的6.26、6.12和6.95 μg/m3增大到24 h的19.41、19.16和21.42 μg/m3。

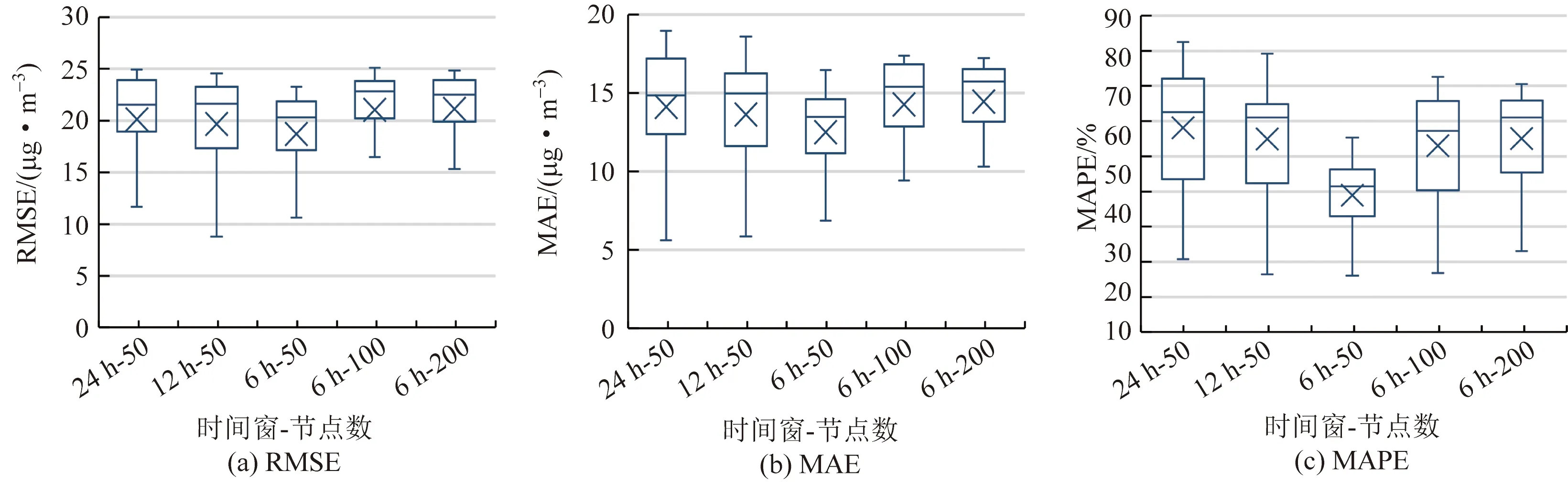
图5 不同时间窗和节点数对hLSTM模型预报精度的影响Fig.5 Effect of different time windows and node numbers on prediction accuracy of hLSTM model

图6 hLSTM模型逐小时预报精度Fig.6 Hourly prediction accuracy of hLSTM model

为研究hLSTM模型预报结果的季节性差异，对于PM2.5预测结果的RMSE按春季(3—5月)、夏季(6—8月)、秋季(9—11月)和冬季(12—次年2月)进行分析，结果如图8所示。由图8可知，hLSTM模型误差存在明显的季节性差异，在所有预报时效上均呈现冬季>秋季>春季>夏季的特征，与确定性方法预报结果类似[35]，其中当预报时效大于3 h时，冬季的预报误差达到夏季的2倍以上。造成这一现象的原因可能是由于长沙冬季受外源输入性污染和本地不利扩散条件共同影响，使PM2.5变化规律更为复杂，增加了hLSTM模型提取数据时序特征的难度。

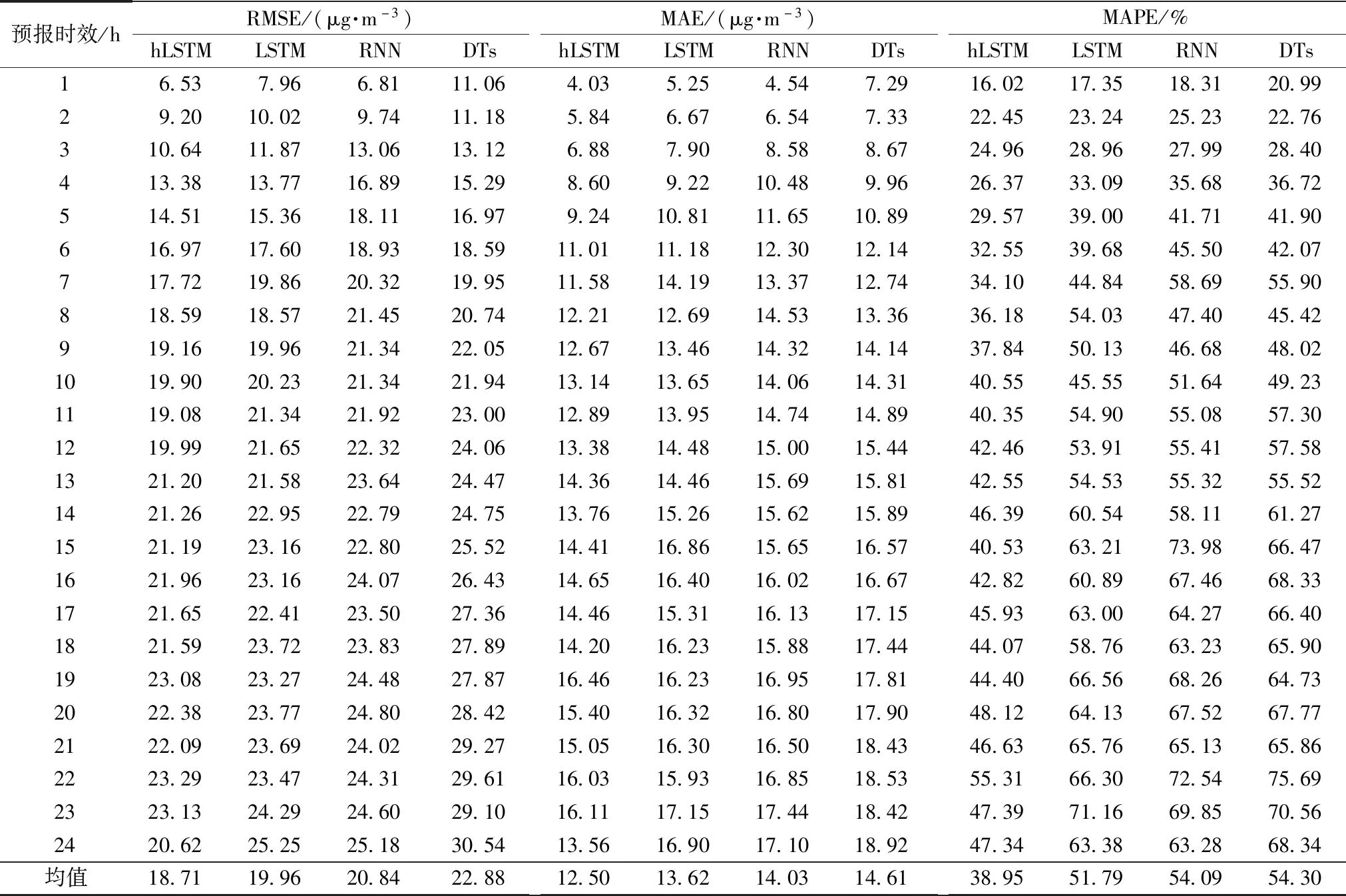
表3 不同机器学习模型逐小时预报精度Table 3 Hourly prediction accuracy of different machine learning models

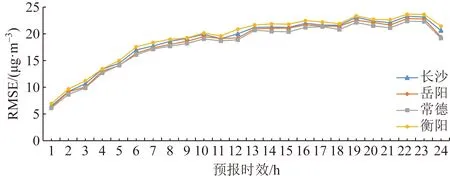
图7 hLSTM模型在不同地区的预报精度Fig.7 Prediction accuracy of hLSTM model in different districts

2.3 污染天气个例预报

由于本地污染排放叠加外来输入影响，长沙市2019年12月13—16日出现以PM2.5为首要污染物的持续性重污染天气过程。以马坡岭空气质量监测站为例，其PM2.5浓度于13日为111 μg/m3，14日夜间上升至189 μg/m3，15日持续重度污染，达到244 μg/m3，16日18:00后迅速下降。利用本研究的hLSTM模型对此次重污染过程进行逐小时预报，选取预报时效为1、2、3、6、12和24 h的预报值和观测值进行对比。如图9所示，6个时效基本都能够预测到本次污染过程的变化趋势，其中3 h内的临近预报结果与观测值吻合程度较高，而6、12和24 h预报值在14日后存在较明显的偏低；1、2、3、12和24 h时效结果对污染过程峰值和消退时间点的预报基本准确，但6 h时效结果对峰值和消退时间的预报则较观测值提前了约8 h。造成这种情况的可能原因一是空气污染物局地小尺度扰动使得针对较长预报时效的时序特征提取难度增大；二是引入的气象因子仅限地面气象要素，不能很好反映污染物传播和扩散的天气条件，进而低估了重污染天气过程中PM2.5浓度。

图8 hLSTM模型不同季节各时效预报精度Fig.8 Prediction accuracy of hLSTM model in different seasons

图9 hLSTM模型对长沙2019年12月13—16日重污染天气过程PM2.5浓度的预报结果Fig.9 PM2.5 concentration prediction results of hLSTM model for the heavy pollution process in Changsha city from December 13 to 16,2019

3 结论

利用Pearson相关系数和自相关系数分析了长沙10个空气质量监测站PM2.5浓度的时空相关性，提出一种以LSTM为主要构成的多变量混合PM2.5浓度逐小时预报模型，利用均方根误差、平均绝对误差和平均绝对百分比误差指标对模型精度进行评估，并与基于DTs、RNN和普通LSTM模型的预报精度进行对比，得到以下结论。

(1)不同的时间窗和LSTM层神经节点数对hLSTM模型精度有显著影响。较大的时间窗会引入更多不相关数据，造成特征信息提取不充分，降低模型训练效率；较多的神经节点使模型更易出现过拟合现象，影响模型泛化能力，二者均会增大hLSTM模型误差。

(2)hLSTM模型误差随预报时效的增加呈现前陡后缓逐步增大，均方根误差、平均绝对误差和平均绝对百分比误差分别从1 h的6.53 μg/m3、4.03 μg/m3和16.02%增大到24 h的20.62 μg/m3、13.56 μg/m3和47.34%。与基于DTs、RNN和普通LSTM模型预报精度进行对比可知，得益于以LSTM层为主体的模型结构和附加信息的引入，hLSTM能够更好地提取长沙PM2.5浓度时序特征，达到更高的预报精度。

(3)hLSTM模型误差存在明显的季节性差异，呈现冬季>秋季>春季>夏季的特征，冬季的预报误差可达夏季的2倍以上。由于空气污染物局地小尺度扰动和地面气象因子无法很好反映污染物传输和扩散条件等因素，hLSTM较易低估重污染天气过程中PM2.5浓度，造成预报精度下降。