超大直径盾构隧道穿越岩溶发育区地表注浆合理加固范围

舒 恒，彭雨杨，宋 明*，刘尚各，阳军生，张 聪

(1.中交第二公路勘察设计研究院有限公司，武汉 430056；2.中南大学土木工程学院，长沙 410075；3.中南林业科技大学土木工程学院，长沙 410004)

随着城市交通建设步伐的不断加快，特别是盾构机械的广泛应用，中国盾构隧道建设进入了高速发展的黄金期[1-2]。然而，受困于地层的复杂性、不均匀性，盾构法施工过程中将不可避免遭遇各类不良地质条件所带来的挑战[3-4]。其中，盾构隧道穿越复杂岩溶区的施工安全问题较为普遍，施工过程中极易发生盾构下沉或偏移、地表隆陷或坍塌、隧道突涌水等工程事故，甚至造成重大经济损失和人员伤亡[5-7]。因此，开展盾构穿越岩溶区安全灾害防控研究，提出合理的盾构隧道穿越岩溶发育区地表注浆加固范围，对于工程建设具有重要意义。

近年来，许多学者针对盾构穿越岩溶区的注浆加固范围的确定做了大量研究，主要包括理论分析、经验类比和数值计算等方法。其中，理论分析方面，陆平等[8]依托武汉地铁6号线红马区间工程，通过分析岩溶塌陷机理，确定了不同地质岩溶发育区的注浆加固范围；李鸿博等[9]以大连5号线跨海隧道为工程依托，结合盾构隧道注浆加固理论和塌落拱理论分析，确定了不同的溶洞位置和充填形式的溶洞注浆加固范围。经验类比方面，研究大多基于特定地区相似工程案例来探讨注浆加固范围的取值，相关学者[10-13]根据工程实际和相关规范，分别结合广州、武汉、大连、南宁地区施工经验，制订了相应工程盾构隧道沿线溶洞处理原则，进而确定了注浆加固范围。数值计算方面，李金奎等[14]以大连5号线后后区间为工程背景，基于数值模拟方法分析了溶洞对盾构掘进的影响，提出掘进面与溶洞之间塑性区贯通距离与溶洞大小呈近线性关系；谢琪[15]以南宁某盾构隧道开挖工程为依托，通过数值模拟方法建立了岩溶隧道安全距离与围岩参数、溶洞高宽、侧压力系数等影响因素关系的预测模型。但遗憾的是，上述研究主要集中在盾构直径小于14 m的工程，而对于超大直径盾构(直径14～18 m)穿越岩溶区注浆加固范围的研究则鲜有报道。考虑中外超大直径盾构隧道的不断增多，开展超大直径盾构穿越岩溶区注浆加固范围的研究具有重要的现实意义和工程价值。

鉴于此，现以某超大直径盾构穿越岩溶发育区为工程背景，设计以围岩等级、溶洞尺寸及溶洞充填范围为影响因素的正交试验，采用三维数值求解不同方位溶洞与超大直径盾构隧道的最小安全距离，并提出以影响最小安全距离主要因素为分段计算准则的地表注浆加固范围确定方法。研究成果可为类似工程确定岩溶合理加固范围提供参考，对于盾构穿越岩溶发育区灾害防控与安全施工具有一定意义。

1 工程概况与岩溶发育特征

1.1 工程背景

武汉市某超大直径盾构隧道工程在里程K8+865～975段将穿越岩溶发育区，该段隧道顶板标高-8.8～-6.5 m，埋深36.5～40.6 m，隧道底板标高-24.3～-22.0 m，埋深52.0～56.0 m，内净空高约15.5 m。区间地貌形态属剥蚀堆积平原区，地势较为平坦，地层自上而下依次为填土层、粉质黏土及黏土夹碎石层、红黏土夹碎石层和灰岩、炭质灰岩、炭质泥岩层，围岩级别为Ⅱ～Ⅴ级，隧道地质纵剖面如图1所示。区域内地下水按含水地层的岩性、赋存条件及水力性质，划分为碎屑岩裂隙水和碳酸盐岩裂隙岩溶水两种类型，岩溶水埋深6.7～8.4 m，水位绝对高程22.34～24.82 m，水头较高且多具承压性，局部富水性较好，可能存在突水、涌泥问题。

图1 某超大直径盾构隧道地质纵剖面图Fig.1 Geological longitudinal section of a super large diameter shield tunnel

1.2 岩溶发育特征

为探明盾构穿越段岩溶的发育特征，并减小对后续盾构的掘进影响，采用盾构掘进线两侧钻探与盾构掘进线内物探相结合的勘探方法。现场勘探反映溶蚀现象较为明显，场地岩溶强发育，以溶隙型溶洞为主，沿线部分地段分布可溶性灰岩，埋深在12.3～16.8 m，揭露溶洞41个，见洞隙率为78.6%，平均线岩溶率为11.7%。

(1)溶洞尺寸特征。溶洞高度统计如表1所示。由表1可知，洞高主要集中在6 m以下，局部较大，且形态不规则。

(2)溶洞分布特征。溶洞与盾构隧道之间的空间位置关系如表2所示。由表2可知，溶洞在隧道洞身、顶板之上，隧道底板之下均有分布，岩溶在水平方向及垂直方向均密集发育，溶洞与隧道的距离分布较为离散，多在8 m以上。

(3)溶洞充填特征。溶洞充填情况如表3所示。由表3可知，区域内溶洞以全充填为主，少量无充填及半充填，岩溶充填度高。岩溶充填物主要为可塑状红黏土，其间夹杂有灰岩碎石，其中红黏土具有上硬下软、含水量高、孔隙比大、高液限、高塑限、低压缩性等特点。

表1 溶洞洞高统计Table 1 Statistics of karst cave height

表2 溶洞与盾构隧道空间位置关系Table 2 Spatial relationship between karst cave and shield tunnel

表3 溶洞充填情况统计Table 3 Statistics of cave filling

2 注浆加固范围数值计算

2.1 三维计算模型建立

三维模型横向(X方向)宽度取120 m、纵向(Y方向)长度取50 m，竖直(Z方向)长度往隧底下取56 m、向上按实际地形取至地表(顶板埋深40 m)。边界约束为模型前、后、左、右水平约束，模型底面竖向约束，模型顶面为自由边界。此外，本计算模型假设围岩和支护结构都为均质、各向同性材料，溶洞简化为球体。计算模型分为围岩、溶洞、充填物、盾构主机钢板、盾构机刀盘、盾构隧道管片以及注浆等代层等网格组。其中，围岩和岩溶内部充填物采用摩尔-库伦本构模型的实体单元进行模拟，溶洞采用圆球形实体单元钝化(model null)进行简化，考虑充填物与岩体之间非连续的接触关系，在二者之间设置接触面单元以模拟材料间的错动与滑移，具体三维计算模型如图2所示。

盾构主机钢板、盾构机刀盘以及盾构隧道管片均采用壳单元模拟，注浆等代层采用实体单元模拟，并考虑主机钢板自重、盾构掌子面掘进压力、刀盘开口率、管片接缝刚度折减及等代层浆液硬化状态。盾构机模型细节如图3所示。

2.2 参数选取

盾构穿越地层主要为填土、粉质黏土、岩层及岩溶充填物红黏土。其中，为进行正交试验分析，将岩层围岩等级简化为Ⅱ、Ⅲ、Ⅳ、Ⅴ共4种，各地层的详细参数如表4所示。

根据现场盾构机选型情况，计算模拟结构单元参数如表5所示。

图2 三维计算模型Fig.2 Three-dimensional calculation model

图3 盾构模型细节Fig.3 Details of shield model

表5 结构单元参数Table 5 Parameters of structural units

2.3 计算工况

根据上述地质特征和岩溶发育特征，采用正交试验设计方法，将围岩等级、溶洞尺寸和充填范围正交试验设计影响因素，分别对溶洞位于盾构隧道上方、溶洞位于盾构隧道侧方和溶洞位于盾构隧道下方3种不同情况进行注浆加固范围求解，试验设计采用3因素4水平的正交试验表，共计16组试验工况，具体正交试验工况设计如表6所示。

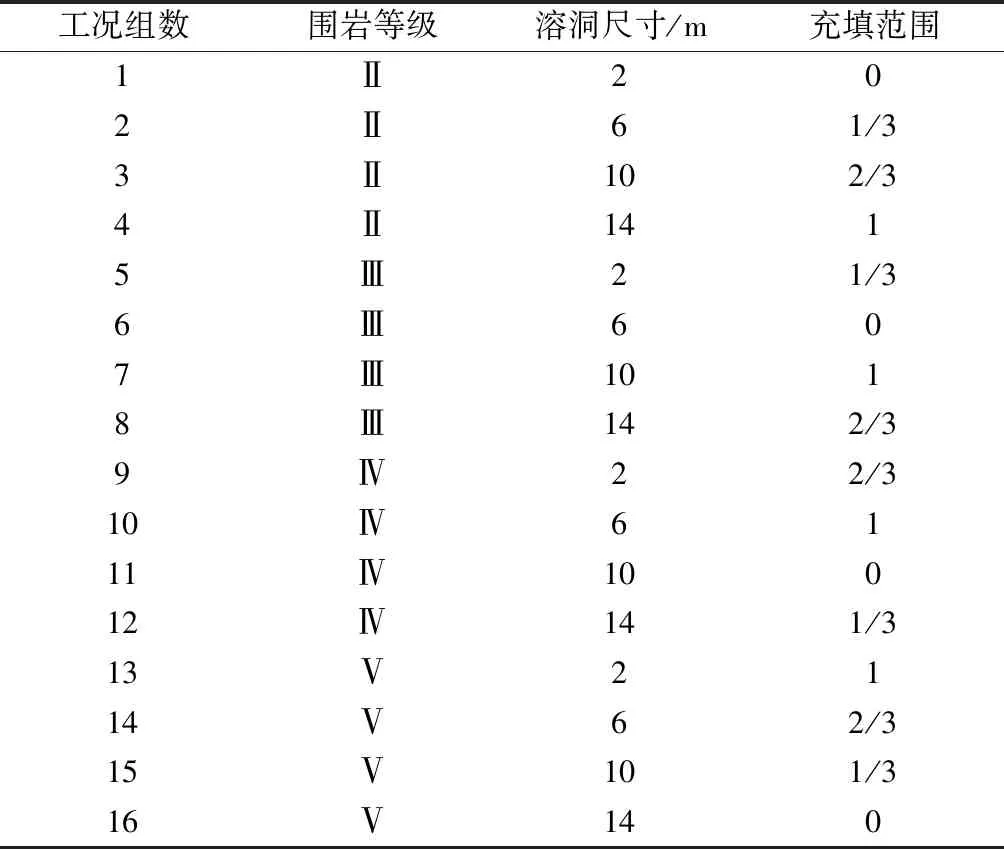
表6 正交试验工况设计Table 6 Orthogonal experimental condition design

2.4 注浆加固范围计算方法

基于数值模拟方法，提出对溶洞位于盾构隧道上方、侧方和下方3种情况分别进行讨论，根据计算和数据分析结果对两湖隧道岩溶段划分区域，对不同区域进行不同范围的注浆加固。其中，各区域注浆加固范围计算方法如图4所示。

以盾构隧道掘进至溶洞球心所在竖向平面为最不利工况，通过调整开挖面与溶洞边界之间的间距，以地层是否出现贯通开挖面与溶洞的塑性区，来判断是否达到溶洞与盾构之间的最小安全距离[14-15]，此即为正交试验要求解的不同工况下的注浆加固范围。

对正交试验结果进行方差分析，确定溶洞位于盾构隧道不同空间位置时注浆加固范围的影响因素排序。

对正交试验结果进行回归分析，得出溶洞位于盾构隧道不同空间位置的注浆加固范围线性回归预测模型。

综合考虑围岩等级、溶洞尺寸、充填范围3个影响因素，根据溶洞位于盾构隧道不同空间位置的最重要影响因素对两湖隧道岩溶段进行注浆区域划分。

基于相应的注浆加固范围预测模型分别计算盾构隧道上方、侧方和下方的各区域注浆加固范围。

图4 计算方法流程图Fig.4 Calculation method flowchart

3 数值模拟结果分析

3.1 溶洞位于盾构隧道上方结果分析

为了计算获得溶洞位于盾构隧道上方的注浆加固范围，需通过不断调节溶洞与盾构隧道距离，直至两者塑性区贯通，此时两者的距离即为注浆加固范围。现以典型工况5为例，围岩等级Ⅱ级，溶洞尺寸2 m，溶洞充填范围为溶洞下方1/3范围，通过前期试算和距离调节，可获得典型工况5下，溶洞与隧道距离为6 m及5 m时的塑性区分布情况如图5所示。

由图5可以看出，当溶洞与盾构隧道距离为5～6 m时，两者塑性区达到贯通状态，为获得更精确的注浆加固范围，采用半分法原理逐步确定塑性区贯通距离所在区间，根据进一步的计算结果，得到典型工况5的注浆加固范围为5.2 m。采用上述计算方法依次对16组工况进行数值计算，获得16组工况下的注浆加固范围，计算结果如表7所示。

图5 溶洞位于隧道上方数值模拟求解示例Fig.5 Numerical simulation solution example of karst located above the tunnel

表7 溶洞位于盾构隧道上方时注浆加固范围计算结果Table 7 Calculation results of grouting reinforcement range when the karst is located above the shield tunnel

3.1.1 方差分析

为了进一步评价和验证围岩等级(因素A)、溶洞尺寸(因素B)以及充填范围(因素C)各影响因素对注浆加固范围的影响，采用SPSS统计分析软件对16组试验结果进行方差分析，结果如表8所示。

表8 溶洞位于盾构隧道上方时注浆加固范围方差分析Table 8 Variance analysis of grouting reinforcement range when karst cave is located above shield tunnel

通过对F分布表进行查询可知：F0.1(3，6)=3.290，F0.05(3，6)=4.760，F0.01(3，6)=9.780。采用F分布进行方差分析显著性检验，可知各因素对溶洞位于盾构隧道上方注浆加固范围均有一定影响，各因素排序为B>C>A。其中，B为显著因素，C为较显著因素，A为不显著因素。

3.1.2 多元线性回归分析

为了定量评价围岩等级(因素A)、溶洞尺寸(因素B)以及充填范围(因素C)对溶洞位于隧道上方注浆加固范围的影响规律，对表7计算结果进行标准化处理，得到溶洞位于盾构隧道上方的注浆加固范围(dabove)与标准化处理之后的各影响因素之间的线性回归方程式为

(1)

由式(1)可知，模型复相关系数R为0.937，表明溶洞位于盾构隧道上方注浆加固范围与围岩等级、溶洞尺寸以及充填范围之间具有较强的相关性。围岩等级和溶洞尺寸与注浆加固范围呈正相关关系，充填范围与注浆加固范围呈负相关关系。

3.2 溶洞位于盾构隧道溶洞侧方结果分析

以典型工况10为例对溶洞位于盾构隧道溶洞侧方结果进行分析。采用前文所述计算方法可获得典型工况10下，溶洞与隧道距离为3 m及2 m时的塑性区分布情况如图6所示。

由图6可知，当溶洞与盾构隧道距离为2～3 m时，两者塑性区达到贯通状态。进一步的计算结果表明，典型工况10下侧方注浆加固范围为2.7 m。

采用上述计算方法依次对16组工况进行数值计算，获得16组工况下的注浆加固范围，计算结果如表9所示。

图6 溶洞位于隧道侧方数值模拟求解示例Fig.6 Numerical simulation solution example of karst cave located on the side of tunnel

表9 溶洞位于盾构隧道侧方时注浆加固范围计算结果Table 9 Calculation results of grouting reinforcement range when the karst is located on the side of the shield tunnel

3.2.1 方差分析

为了进一步评价和验证各影响因素对注浆加固范围的影响，采用SPSS统计分析软件对16组试验结果进行方差分析，结果如表10所示。

表10 溶洞位于盾构隧道侧方时注浆加固范围方差分析Table 10 Variance analysis of grouting reinforcement range when karst cave is located on the side of the shield tunnel

通过对F分布表进行查询可知：F0.1(3，6)=3.290，F0.05(3，6)=4.760，F0.01(3，6)=9.780。采用F分布进行方差分析显著性检验，可知各因素对溶洞位于盾构隧道侧方注浆加固范围均有一定影响，各因素排序为A>B>C。其中，A为显著因素，B为较显著因素，C为不显著因素。

3.2.2 多元线性回归分析

对表9计算结果进行分析，得到溶洞位于盾构隧道侧方的注浆加固范围(dside)与标准化处理之后的各影响因素之间的线性回归方程式为

(2)

由式(2)可知，模型复相关系数R为0.873，表明溶洞位于盾构隧道侧方注浆加固范围与围岩等级、溶洞尺寸以及充填范围之间具有较强的相关性。围岩等级和溶洞尺寸与注浆加固范围呈正相关关系，充填范围与注浆加固范围呈负相关关系。

3.3 溶洞位于盾构隧道下方结果分析

以典型工况15为例，对溶洞位于盾构隧道溶洞下方结果进行分析。采用前文所述计算方法可获得典型工况15下，溶洞与隧道距离为10 m及9 m时的塑性区分布情况如图7所示。

图7 溶洞位于隧道下方数值模拟求解示例Fig.7 Numerical simulation solution example of karst cave located under the tunnel

由图7可知，当溶洞与盾构隧道距离为9～10 m时，两者塑性区达到贯通状态。进一步的计算结果表明，典型工况15下侧方注浆加固范围为9.8 m。

采用上述计算方法对16组工况进行数值计算，获得16组工况下的注浆加固范围，计算结果如表11所示。

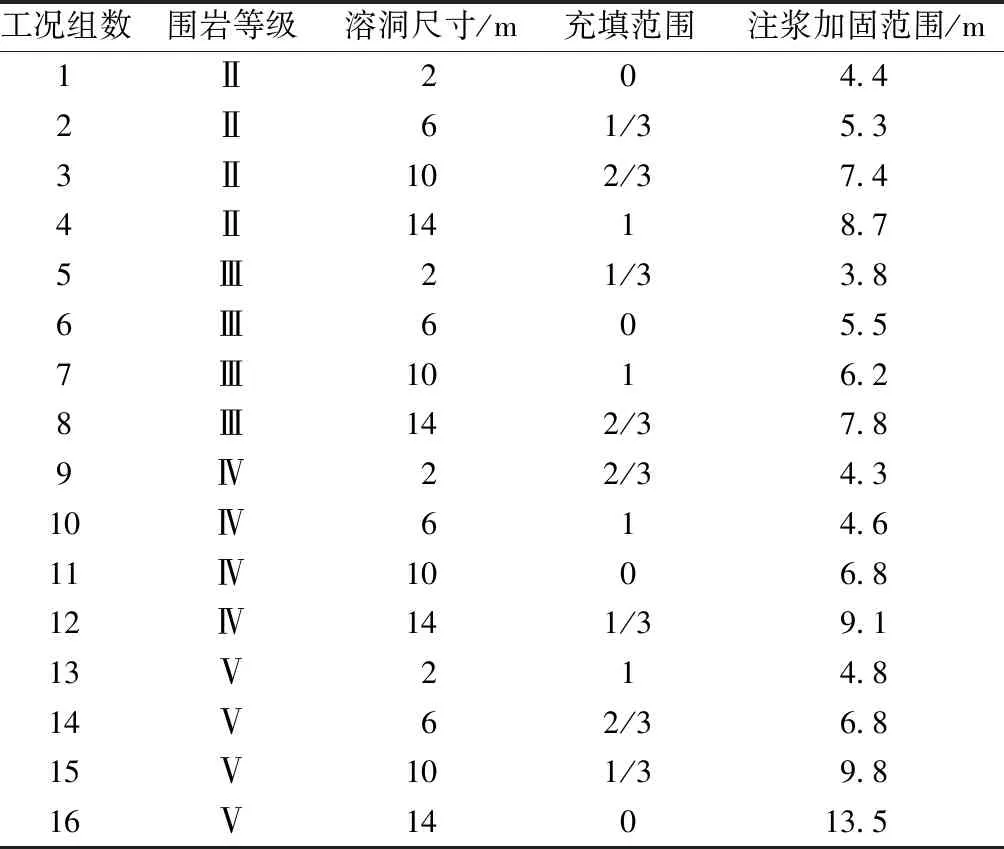
表11 溶洞位于盾构隧道下方时注浆加固范围计算结果Table 11 Calculation results of grouting reinforcement range when the karst cave is located under the shield tunnel

3.3.1 方差分析

为了进一步评价和验证各影响因素对注浆加固范围的影响，采用SPSS统计分析软件对16组试验结果进行方差分析，结果如表12所示。

表12 溶洞位于盾构隧道下方时注浆加固范围方差分析Table 12 Variance analysis of grouting reinforcement range when karst cave is located under the shield tunnel

通过对F分布表进行查询可知：F0.1(3，6)=3.290，F0.05(3，6)=4.760，F0.01(3，6)=9.780。采用F分布进行方差分析显著性检验，可知各因素对溶洞位于盾构隧道下方注浆加固范围均有一定影响，各因素排序为B>A>C。其中，B为显著因素，A为较显著因素，C为不显著因素。

3.3.2 多元线性回归分析

对表11计算结果进行分析，得到溶洞位于盾构隧道下方的注浆加固范围(dbelow)与标准化处理之后的各影响因素之间的线性回归方程式为

(3)

由式(3)可知，模型复相关系数R为0.916，表明溶洞位于盾构隧道下方注浆加固范围与围岩等级、溶洞尺寸以及充填范围之间具有较强的相关性。围岩等级和溶洞尺寸与注浆加固范围呈正相关关系，充填范围与注浆加固范围呈负相关关系。

上述回归分析结果中，隧道与溶洞的最小安全距离的线性关系与相关性与现有研究成果[14-16]基本相符，但超大直径盾构穿越岩溶发育区时，最小安全距离在最主要影响因素等方面仍表现出不同的规律。

3.4 分段注浆加固范围计算

方差分析结果表明，溶洞位于盾构隧道上方及下方注浆加固范围的主要影响因素均为岩溶尺寸，溶洞位于盾构隧道侧方注浆加固范围的主要影响因素为围岩等级和岩溶尺寸。因此，计算时均以岩溶尺寸作为主要区域划分标准。根据武汉市某超大直径盾构隧道上方、侧方以及下方的最大溶洞尺寸，并考虑围岩等级与充填情况以及安全系数(K取1.2，考虑实际施工方便对于计算结果小数大于0.5的取1，对于小于0.5的按0.5取值)。其中，为确保施工安全，即使划分区域内无溶洞发育，考虑武汉市盾构隧道岩溶高风险区(盾构隧道上方5 m、侧方5 m及下方8 m范围)内均需注浆加固处理。综合考虑计算获取的盾构隧道上方、侧方及下方不同区域注浆加固范围和高风险区注浆加固范围，得到武汉市某超大直径盾构隧道穿越岩溶发育区注浆加固范围如表13所示。此外，获得的注浆加固范围与中外已建成的类似工程[9-12]较为接近。

表13 不同岩溶区域盾构隧道上方、下方注浆加固范围Table 13 Grouting reinforcement range above and below shield tunnels in different karst sections

4 结论与建议

(1)基于正交试验设计，并采用三维数值计算求解了不同方位溶洞与超大直径盾构隧道的最小安全距离，分析得到了围岩等级、溶洞尺寸、充填范围各影响因素排序及其线性回归方程式。当溶洞位于隧道上方、侧方及下方时，最小安全距离主要影响因素分别为溶洞尺寸、围岩等级及溶洞尺寸。

(2)依托典型工程提出了以最小安全距离主要影响因素为分段计算准则的地表注浆加固范围确定方法，并用于指导工程实践。计算获得的注浆合理加固范围：当溶洞位于隧道上方时，分为4个区段，加固范围在12～22.5 m，当溶洞位于隧道侧方时，分为4个区段，加固范围在8～15 m，当溶洞位于隧道下方时，分为5个区段，加固范围在8～15.5 m。

(3)提出的注浆加固范围计算方法在保证盾构施工安全的同时，提高了浆液利用率，具有较高的社会经济效益和广泛应用前景。但值得注意的是，该方法在计算过程中对岩溶地层进行了简化模拟，忽略了岩溶地层的复杂性与不均一性，如岩溶充填类型、溶洞真实形态、裂隙管道等。此外，影响注浆加固效果的因素众多，该方法仅针对部分主要影响因素进行了探讨。因此，后续研究应充分考虑地层特点和工程实际进一步优化计算模拟。