用“思维”让学生“看见”图形——兼评《认识线段》教学设计

文|潘小福（特级教师）

几何学概念的基础是图形，图形相对于数量而言似乎更为直观，因此在几何图形的概念教学中，我们一直存在一个认知偏差，总认为几何学概念更容易感知对象，相对于代数而言更容易抽象。事实上，事物越是直观，越是与日常生活联系密切，抽象就越难。因此，在认识图形的教学过程中，尤其是低年级学生，需要通过丰富的实践和操作活动，积极引导学生开展抽象、想象、描述等数学思维活动，才能用“思维”让学生“看见”图形。

一、现象与本质的思考

复旦大学王德峰教授在一次“西方的知识是怎么来的”主题讲座中，举了“水结成冰”的例子，“水”和“冰”都可以通过感官知觉到，而“结成”是无法直接感知的，需要通过思维才能形成概念，并成为经验。由“水结成冰”引发了我们关于几何学概念教学的现象与本质的思考与探讨。

关于几何学概念的抽象问题，数学历史发展中有着“唯实论”和“唯名论”的争论。柏拉图认为通过肉眼看到的图形是一般意义上存在的图形的影子，一般意义上的图形是真正存在的，这种存在要通过“思想”才能“看”到。作为柏拉图的学生，亚里士多德却认为，一般概念是人从感性的经验中通过直观和抽象获得的，这些一般概念只存在于我们的主观意识之中，而不是看得见摸得着的客观存在。“唯实论”“唯名论”的争论旷日持久，各有价值。但是从几何学概念的教学角度而言，都要关注现象与本质，让学生从感性经验出发，然后通过数学的方法，经历思维的过程，获得更为一般的几何学概念。

历来，小学数学教材也正是这样进行编写的。以苏教版教材为例。图1为一年级下册《认识图形（二）》的教材，先让学生玩积木，积累起充分的感性经验，再让学生把长方体上的面画下来，形成对图形的直观感知，为了让学生初步形成长方形的概念，必须借助于数学的抽象，引发学生数学思维：从长方体上画下的面都是长方形吗？从长方体不同的面上画出的长方形是不一样的，但都可以用怎样的图形来表示？长方形还可以有不一样的吗？帮助学生跳出“影子”或“客观存在”，由现象至本质，初步认识到“长方形”是“一般概念”，不是某一具体的存在，是“思想”的“产物”。

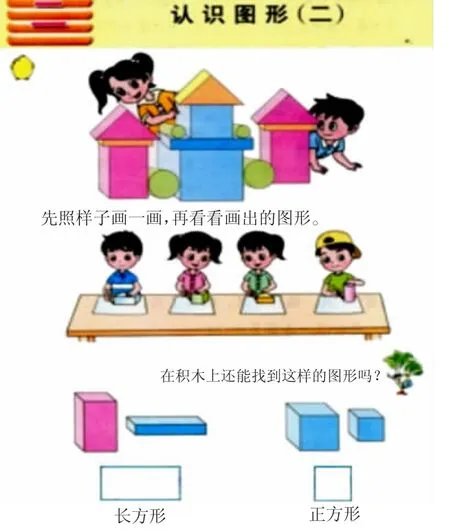
图1

类似的，苏教版二年级上册“厘米和米”单元第一课时《认识线段》的教材（如图2），也是通过“拉一拉”“找一找”“折一折”“画一画”等一系列活动，从感性的经验中感悟、体验线段的本质属性，形成线段的一般概念。特别是“折一折”的活动，把线段置于平面图形中，还原线段作为构成平面图形要素的本来面目，引导学生正确把握线段的概念恰到好处。

图2

二、内容到目标的解析

基于小学生的年龄特点及认知规律，以“思”“见”图的要求是逐步递进的，“思”的方法，“见”的程度都是分阶段达成的，不是一次性完成的。因此，每一几何学概念的编排都是螺旋式的，教学目标都是阶段递进，其内在存在着特定的结构性与逻辑递进性。

内容编排螺旋上升。小学阶段教学几何学的概念，都会根据学生的年龄特点，采用螺旋上升的方式分成几段教学，让认识逐步深化。例如，苏教版教材对几何学概念的编排有着独有的体系，先是直观认识立体图形，整体感知立体图形的形状，识别这些图形，形成初步的表象，并初步感知平面图形和曲面图形的区别；然后再通过在立体图形上找平面图形的方式，直观认识平面图形，整体感知，形成初步表象，初步感知直边图形和曲边图形的区别；在此基础上，直观认识“线段”和“角”，通过构成图形的要素——“边”和“角”，认识平面图形；在认识图形的特征时，先认识长、正方形的特征，继而深入认识“线段、直线、射线”“角”“垂直与平行”，再认识平行四边形、三角形、梯形、圆的特征，并把轴对称图形、旋转与平移、图形的放大与缩小穿插其中，形成对平面图形的完整认知。这样的编排不追求一下子让学生全部“看清”图形，而是在学生的最近发展区内，开展适切的思维活动，恰当地“见”到图形。

教学目标阶段递进。循着螺旋上升的教学内容的编排，相应的教学目标也是分学段逻辑递进的。第一学段的教学目标主要是“辨认”立体图形或平面图形，“初步认识”长方形和正方形的特征，“了解”直角、锐角和钝角。第二学段的教学目标主要是“认识”三角形、平行四边形、梯形和圆，“认识”长方体、正方体、圆柱和圆锥，“知道”平角与周角，“了解”平面上两条直线的平行和相交（包括垂直）关系。按照《数学课程标准（2011年版）》的设计，作为结果目标的行为动词，“了解”“知道”和“初步认识”是同类词，是指“从具体实例中知道或举例说明对象的有关特征；根据对象的特征，从具体情境中辨认或者举例说明对象”。“认识”和“理解”是同义词，是指“描述对象的特征和由来，阐述此对象与相关对象之间的区别与联系”。第一学段，学生对图形的认识主要定位于结合具体实例，能够辨认或举例说明，即对图形形成整体的、直观的认识。第二学段，学生对图形的认识不仅能够描述图形的特征，还要能够阐述图形之间的区别与联系，形成相应的认知结构，即对图形形成分析的、抽象的甚至关联的认识。

基于此，对二年级上册“认识线段”的教学，要从整体上理清教材的编排，要依据学段把握“直观认识”的教学目标。苏教版教材对“线段的认识”是分两次编排的，一次是在二年级上册“厘米和米”单元，第二次是在四年级上册“垂线与平行线”单元。二年级时，通过丰富的“做数学”活动，在充分的直接经验的基础上，形成“直直的”“有两个端点”的认识，并据此能够“辨认”出线段来，特别是初步理解到线段是构成其他平面图形的要素，要能初步脱离具体事物“想象”出线段；而到四年级时，不再借助直观感知经验，通过线段的端点向一边或两边无限延长，引出射线、直线，借助数学的思维，理解几何概念之间的联系。只有整体把握了教材的编排和教学目标，才能在二年级时准确定位目标，运用恰当的学习方式让学生“思”得起来，也才能“见”得合理。

三、经历至思维的升华

以“思”“见”图，“思”就是要培养学生对几何学概念的抽象、归纳能力，这种能力不是与生俱来的，必须要系统培养，只有这样，才能真“见”到几何学概念的本质，而不是只看到它们的“影子”，造成认知上的偏差，也影响几何学概念认知结构的形成。因此，在小学阶段要重视学生经历“做数学”的过程，通过数学操作、数学体验及数学实验活动，让学生对几何学概念形成丰富的感知经验，但不能仅此而已，还要引发想象、比较、推理等数学思维，在动手动脑“做数学”的过程中以积极的“思维”去主动“看见”图形。

以二年级上册《认识线段》一课为例，从“看见”图形的角度，有这样三层目标：第一层是判断画出的线是不是线段（根据是不是直直的来判断）；第二层是数出已知的平面图形中由几条线段围成；第三层是数一数图形中有几条线段，并因此对图形进行命名或分类。毕竟是二年级的学生，从“思维”的角度而言，还只能从直观例子中抽象出“直直的”“有刻画长度的端点”，因此，通过拉一拉、找一找、折一折、画一画等具体动作思维进行简单的抽象、归纳，让学生“看见”线段，形成适切的线段的认知。

以王妍和王丽娟两位教师的《认识线段》教学设计为例。我们可以看到两位教师是如何让学生经历“做数学”的过程，实现经历到思维的升华。

王妍老师在教学中有这样几个层次：第一层，通过拉、找、想，形成表象。以比较两条随意摆放在桌上的线的长短作为学习的开端，组织学生进行“拉一拉”的活动，形成“线段是直直的”的表象，这是可以感知的经验；继而从表象出发，先引导学生从数学课本的封面上“找一找”，并从正确“比划”的角度，帮助学生认识线段的“两个端点”，在此基础上，通过“激光笔投射”“水滴的滴落”想象线段，虽然“看不见”，但可以“想象”，这一有创意的活动为学生今后形成对“线段”概念的科学认知种下“慧根”。第二层，通过数、折、比，深化认知。教师把线段置于平面图形之中，回归线段是构成平面图形的要素的本质，通过数一数知道正方形是由四条线段围成的平面图形，并通过“折一折”“比一比”来深入认识线段，理解线段“有长有短”。第三层，通过画一画，多元表征。在充分的实践和操作活动之后，开展“画一画”活动，把实践和操作的经验，进行归纳抽象，把通过“思维”“看见”的图形用图表征出来，并通过方向、长短的变式多元化表征，帮助学生抽象成线段的概念。整节课，既有充分的操作、实践活动，更有恰到好处的思维活动，有效地帮助学生形成“一般的概念”。

王丽娟老师的教学设计也有三个层次。第一层，试画图形，整体入手。从画平面图形开始，先让学生感知到线段是构成图形的要素。第二层，拉、找线段，初步感知。这一层是结合实践体验活动初步认识线段，通过“拉一拉”“找一找”活动，用感知积累起线段是“直直的”的直接经验。第三层，画画想想，深入建构。这一层王老师重点放在了“画线段”上，这是低年级学生很适合的几何图形抽象的有效方式，是把建立起来的感知经验，经过数学思维，用自己喜欢的方式表征出来，并通过与班级同学的互动交流，形成完整的概念。王老师在这一环节上，特别地跟进了三个层次的问题探索：第一，你是怎么画的？沿着直直的边画；第二，这些线段有什么相同点？都是直直的；第三，这些线段又有什么不同点？有直、有横、有斜，方向不同；有长有短，长度不同。学生画画想想，多视角的思考表征，让学生思维由单一走向纵深。最后规范画法：画出两个端点。在教师针对性的引领之下，学生手脑并用，以做促思，对线段的认识从经验感知逐步上升至理性思维，进而建构数学概念。

两位教师的教学设计虽有不同，但都重视在充分感知、建立直接经验的基础上，融入抽象、想象、多元表征等思维活动，凸显以“思”“见”图意旨，有效建立起图形的基本要素———“线段”这一概念。