指向深度学习的『三勤』学习策略
2021-09-26徐素珍余泽仙
文|徐素珍 余泽仙
深度学习是指学生深入本质,能实现自主迁移的学习。从学生学习行为的角度来说,自主提问、同伴合作、思维表达是深度学习的重要表现特征。为了准确把握小学生深度学习方面的状况,笔者对本校的五年级学生进行了问卷调查,统计数据表明,学生的深度学习能力不强,针对问题,笔者进行了《指向深度学习的“三勤”学习策略研究》的实践,主要运用勤提问、勤合作、勤表达这三种学习策略,使学生的质疑问难能力提高,合作交流意识增强,语言表达能力提升,从而使学生的深度学习能力日益增强。
一、勤提问,训练质疑问难能力
通过数学学习,应使学生在提出问题、分析问题、解决问题以及交流和反思方面获得发展。课堂提问是数学教学的重要手段,是师生进行对话、交往互动的纽带。因此,在教学中教师要营造质疑的氛围,让学生敢问、善问、能问。
1.知识生长处勤提问。
学生提出有价值的问题比解决数学问题更为重要。教师在知识的生长处要给予足够的时间,让学生根据数学信息提出有价值的问题,进而让学生围绕问题进行探究,从而促进学生思维的发展。
【案例1】《减法性质》教学片断。
师:同学们已经学习了一个数连续减去两个数,等于一个数减去这两个数的和。根据减法性质,你能提出什么数学问题?
生:学习减法性质有什么用?
生:减法性质可以逆用吗?
生:减法性质可以改成一个数连续减去几个数,等于一个数减去这几个数的和吗?
师:20000-1-2-3-4-……100=?运用减法的性质能把这个问题解决吗?
学生学习了减法性质后,教师创设了学生提问的空间,学生提出了多个有价值的问题,然后学生便围绕这几个问题展开研究。这样设计,学生在发现问题、提出问题、分析问题、解决问题的过程中培养了问题意识。
2.图式表征处勤提问。
在小学数学教学过程中教师应该渗透数形结合思想,在图式表征处让学生提出各种各样的问题,然后围绕问题展开自主探究,培养学生的问题意识和应用意识。
【案例2】在一个长、宽、高分别为40厘米、50厘米、60厘米的长方体水箱中有A、B两根进水管,先开A管,经过一段时间后两管同开。下面折线统计图表示进水情况,请根据折线统计图提出数学问题并解决问题。(见图1)
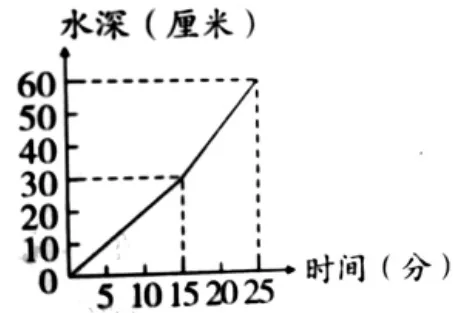
图1 折线统计图
师:仔细观察这幅折线统计图,你能提出什么数学问题?
生:A、B两根水管一起开放,每分钟进水多少?A管独自开放呢?
生:A、B两管齐开,每分钟进水多少毫升?
生:A、B两管齐开每分钟进水比A管单开要多多少毫升?
生:A、B两管齐开每分钟进水比A管单开每分钟进水要多百分之几?
教师先请学生独立解决这四个问题,接着小组内交流各自想法,最后分享成果。
学生根据数学信息提出了层层递进的四个数学问题并一一解决,学生在提出问题和解决问题的过程中发展了思维,提升了深度学习力。
3.知识关键处勤提问。
教师在知识关键处创设学生提问的平台,使学生提出值得研究的问题,并围绕问题自主探究与合作交流,使学生的深度学习能力不断增强。
【案例3】《圆的面积》教学片断。
师:请同学们观察图2,能提出什么问题?
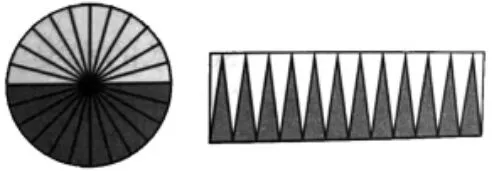
图2 圆转变成近似的长方形
生:近似长方形的长相当于圆的什么?宽相当于圆的什么?圆的面积与近似长方形的面积相等吗?
生:长=圆周长÷2,宽=半径,圆面积=长方形面积,所以圆的面积=圆周长的一半×宽=圆周率×半径×半径=圆周率×半径的平方,用字母表示为S=πr2。
师:请同学们观察图3,能提出什么问题?并与同桌交流。
生:梯形的上底与下底的和是圆周长的一半,梯形的高相当于圆的2条半径,梯形的面积等于圆的面积。圆的面积即S=2πr÷2×2r÷2=πr2。
师:请同学们观察图4,能提出什么问题?

图4 圆转变成三角形
生:三角形的底和高相当于圆中的什么呢?面积有没有发生变化?
生:通过观察,我知道三角形的底就是圆的周长,三角形的高就是圆的半径,面积是相等的。即S=ah÷2=2πr×r÷2=πr2。
教师依次呈现三幅有代表性的图,请学生观察图形并提出数学问题和解决问题。学生在分享聆听的过程中掌握了三种圆面积计算公式的推导方法,使学生的思维得到拓展和延伸,学生的数学核心素养也得到培养。
二、勤合作,提升合作交流意识
动手实践、自主探索、合作交流是小学生学习数学的重要方式。因此,教师在教学过程中要给学生创设利于表达交流的平台,使学生在表达的过程中实现学习资源的共享,从而促进学生共同发展。
1.合情推理勤合作。
推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式。发展学生的推理能力,对于他们适应社会和进一步发展有着重要的作用。
【案例4】六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有ABC;第二次有BDF;第三次有AEF。请问哪两位班长是同班的?
用数字1表示到会,用数字0表示未到会。

A B C D E F第一次1 1 1 0 0 0第二次0 1 0 1 0 1第三次1 0 0 0 1 1
师:请你们根据题目的条件把表格填写完整,然后推理得出哪两位是一个班,并在小组内进行交流,然后派代表分享。
生:因为一起开会的不可能同班,那么A不可能与B、C、E、F同班,所以A与D同班;B不可能与A、C、D、F同班,所以B与E同班;F不可能与A、B、D、E同班,所以F与C同班。
生:从第一次开会情况可以推出A可能与D、E、F同班,从第二次开会情况可以推出A可能与B、D、F同班,从第三次开会情况可以推出A可能与B、C、D同班,由此可见A与D同班。用这样的方法依次类推,可以得出B与E同班、C与F同班的结论。
学生经历了独立思考、讨论交流、分享汇报等数学活动。学生在聆听、分享的过程中提升了抽象逻辑思维能力和推理能力。
2.活题解决勤合作。
合作学习既是学习取得成功的条件,也是一种重要的学习方式。合作学习促进学生之间互帮互助,学习资源实现优化。因此,教师要多设计一题多解的应用题,让学生在小组内分享自己的解题思路,然后派代表汇报,通过这样的分享汇报促进学生深度学习。
【案例5】要修一条长1800米的水渠,工作5天后,已修的长度与未修的比是2∶3,照这样的进度修下去,还要多少天才能修完这条水渠?
师:画出线段图,分析数量关系,解决问题,并在小组内进行分享。
师:请小组派代表进行分享。
生:5÷2=2.5,2.5×(2+3)=12.5(天),12.5-5=7.5(天)。
生:5∶2=2.5,2.5×3=7.5(天)。
生:3∶2=1.5,1.5×5=7.5(天)。
教师设计了一道可以用多种方法解决的问题,学生通过自主思考、合作交流、分享成果等环节,探索出了份数解题、倍比解题、按比例分配解题等多种方法,使学生的思维进阶,提升了学生数学的学习力。
3.名题探究勤合作。
合作学习是一种新型的学习方式。在教学中,教师应选择合适的内容实施有效的合作学习,使学生在合作学习中提升思维、发展能力,促进核心素养的提高。
【案例6】笼子里有若干只鸡和兔,从上面数,有8个头,从下面数,有26只脚,鸡和兔各有几只?
师:在《预学单》上选择喜欢的方法解决,并在小组内进行交流,然后派代表分享。
生:我用画图法画出了兔5只,鸡3只。
生:我用列表法。在表格中先填8只鸡,0只兔;接着填7只鸡,1只兔;这样依次填,就得出3只鸡和5只兔。
生:我是跳跃式列表,从4只鸡和4只兔开始列表的,根据脚的只数对鸡和兔的只数进行调整从而得出结果。
生:假设全是鸡,脚有16只,比26只脚少10只脚,又因为一只鸡比一只兔少2只脚,那就把5只鸡换成5只兔,鸡就是3只。
教学古代名题“鸡兔同笼”时,教师让学生用自己喜欢的方法探究问题,而后进行成果的分享,学生在倾听思考的过程中进一步理解了画图法、按序列表法、跳跃列表法、假设法等多种方法,最后对方法进行优化,使学生感受到解决鸡兔同笼问题的最佳方法是假设法。通过合作学习,取长补短,发挥了团队的力量。
三、勤表达,提升语言表达能力
教师应在概念建构、公式推导、难题破解等教学过程中,让学生充分地表达自己的想法,通过表达的训练,使学生的表达能力螺旋式上升。
1.概念建构勤表达。
数学概念是客观世界中事物的空间形式和数量关系的本质属性在人脑中的反映。教师要提供学生建构数学概念的现实背景和数学材料,通过观察、分析、比较、概括和归纳等数学活动,让学生在概括和归纳概念的过程中提升语言表达能力。
【案例7】《三角形的认识》教学片断。
师:判断下面图形是不是三角形,并说出理由。(课件呈现)

图5 典型的图形
生:图①是三角形,因为它是由三条线段围成的图形。
生:图②不是三角形,有一条线是弯曲的。
生:图③不是三角形,相邻两条线段的端点没有相连。
师:请你们根据刚才判断是不是三角形的理由思考三角形的概念。
生:由三条线段围成的封闭图形叫做三角形。
生:有三条边和三个角的图形叫做三角形。
生:由三条线段围成的(每相邻两条线段的端点要相连)图形叫做三角形。
三角形概念教学时,教师没有直接告诉学生三角形的概念,而是搭建了学生表达的平台,先让学生判断所给图形是不是三角形,然后再请学生根据判断的理由进行辨析思考,概括出三角形的概念,这样安排教学环节,可以促进学生自主建构三角形的概念。
2.公式推导勤表达。
教师要让学生经历公式形成的全过程,要提供适合学生的学习材料,创设学生交流和表达的机会,通过语言将学生的想法进行表达,促进学生高阶思维的形成和发展。
【案例8】《三角形的面积》教学片断。
生:两个相同的三角形拼成平行四边形,三角形的底和高分别等于平行四边形的底和高,因此三角形的面积等于=底×高÷2。

图6 转化为平行四边形
生:先画出三角形ABC的中位线DE,延长DE至F,使DE=EF,连接CF,原来三角形ABC的面积等于平行四边形的面积,三角形ABC与平行四边形的底相同,平行四边形的高与三角形高之比为1:2,所以三角形的面积=底×高÷2。

图7 转化为平行四边形
生:找到AB和AC边的中点,过点A作BC边的平行线EG,再画出平行线之间的距离EH和GR,然后将三角形BHD旋转到AED处,将三角形FCR旋转到FAG处,长方形EHRG的面积与三角形ABC的面积相等。长方形的长就是三角形的高,宽就是三角形BC的一半,所以三角形的面积=底×高÷2。

图8 转化为长方形
学生通过独立思考、动手实践、自主探索等数学活动,用拼组法、剪拼法和割补法推导出三角形的面积公式。学生在充分表达每一种公式推导的过程中,思维的宽度和广度得到了拓展。
3.难题破解勤表达。
在教学难题的过程中,教师先让学生经历独立思考的过程,再让他们经历交流和分享,引导学生用规范的形式进行表达,促进学生抽象逻辑思维的发展。
【案例9】求下面物体的体积,见图9。

图9 不规则物体
生:高为8厘米圆柱的体积再加上高为2厘米圆柱体积的一半就是不规则物体的体积。
生:两个这样的形状可以拼成高为18厘米的圆柱,用这个圆柱的体积除以2。
生:先把这个不规则物体熔铸成一个高为9厘米的圆柱,求出圆柱的体积即可。
学生在用分割法、叠加法、熔铸法解决这道难题的过程中,不断完善自己的知识结构,学生的表达力、思维力、学习力都得到了大幅度提升。
教学实践证明,“三勤”学习方式的确是培养学生问题意识、发展学生合作交流能力、提高学生语言表达能力的有效学习方式。
