留有『新悬念』，让学习在持续、主动的探究中走向深刻——以《三角形的秘密》教学为例

文|管小冬

小时候听单田芳先生的评书，印象最深的是每到情节紧要处，他便会来句“欲知后事如何，请听下回分解”，让人恨不得把他从收音机中揪出来，讲个究竟，道个明白。后来才知道，这叫“悬念”，是文艺作品中常用的一种表现技法，指“读者、观众、听众对文艺作品中人物命运的遭遇，未知的情节的发展变化所持的一种急切期待的心情”。单先生在讲评书时，于关键处断章，让大家欲罢不能，不知不觉就成了他的“追星族”，运用的就是设置“悬念”的技法。

成为教师，有了些经验后，再回想起儿时的这种经历时，便想着如果教学中我们也能像单先生那样，时时都能给学生留有“新悬念”，让他们的数学学习“一波方平，一波又起”，那么，在这样的体验中所进行的数学探究，一定会是件持久的趣事，学习也一定会在他们持续、主动的探究中不断走向深刻。

为什么这样认为呢？

首先，“悬念”意味着一个新问题的发现与提出。爱因斯坦曾经说过：“提出一个问题往往比解决一个问题更重要。因为解决一个问题也许仅是一个数学上或实验上的技能而已，而提出新的问题，却需要有创造性的想象力，而且标志着科学的真正进步。”《数学课程标准（2011年版）》（以下简称“课标”）也指出，“学生自己发现和提出问题是创新的基础”。“课标”中的课程目标由原来的“两能”变为“四能”，也正是意在突出“发现和提出问题的能力”在学生数学核心素养的培养与发展方面的重要作用。留有“新悬念”便是指学生在对某一数学问题或现象的探究过程中，在观察、思考、分析与交流的基础上，又有了新的发现，进而提出了与当前问题相关联的新问题，并且对解决问题、寻求结果有着强烈的心愿。这种强烈的心愿会驱使他们主动投入到持续、深入的探究中去。

其次，“悬念—发现—新悬念—新发现”这种循环递进的学习与探究，契合真实环境下的学习与研究进程。1896年，铀元素放射性质的研究给居里夫人留下了“新悬念”———“一定还有别的元素也具有同样的放射性质”。这一悬念驱动她继续研究并发现了钍元素，同时又留下一个“新悬念”，即一定有一种比铀和钍的放射作用强得多的未知元素。进而她才在研究中发现了镭，为人类探索原子世界的奥秘打开了大门，并由此诞生了一门新的学科——放射学。居里夫人的这一研究历程告诉我们：在真实而复杂的问题研究中，往往会有新感悟、新发现，进而生成新问题，形成新悬念。这些新感悟、新发现、新问题、新悬念会催生我们不断加深对研究的热情与动力，进而进入新的境界。

然而，回顾我们的现实教学，往往却很少能引领学生感受与经历这一点。教师常常会拘泥于具体的课时教学内容，带领学生就问题解决去研究问题解决。以《三角形的三边关系》教学为例，教师创设与之密切相关的问题情境，引导学生发现问题、提出问题、分析并解决问题。在得出“三角形两边之和大于第三边”的结论后，研究就戛然而止，随后的练习都指向结论的深化理解与巩固应用。过于明晰的教学内容划分，过于聚焦的教学目标指向，让教师忽视了即使在对某一具体数学问题的研究中，学生仍然有可能在观察、思考、辨析与交流中，形成一些与当前问题相关联，但却看似没有直接作用的新发现与新悬念。要知道，恰恰是这些看似没有直接作用的新发现、新悬念，会催生学生继续学习与研究的热情与动力，推动着他们的数学学习与研究不断向更深、更广处迈进。而这样的学习与研究，才是指向于“未来生活中，真实而复杂情境下的问题解决”的“真学”，意味着学生创新意识的萌发，问题解决能力的提升，数学核心素养的形成与发展。再次，以“新悬念”推动学生持续、主动、深入地展开数学学习与探究，回应了当下教学中对儿童主体性的召唤。成尚荣先生在《儿童立场》一书中写到：“小学教育好比一扇门……小学教育就是引导学生一次又一次地叩开这扇门，推开这扇门，迎接一个又一个新日子和新世界。”显然，“怎样引导？”“以何种方式叩门？”都是值得我们思考与研究的问题。给学生的数学学习留有“新悬念”，就是引导他们在主动观察与思考中发现不同的“叩门”方式，激发他们“一次又一次叩开这扇门”的热情，引领他们主动去“叩门”，进而发现一个又一个更新的世界。情境教育创始人李吉林老师曾说：“儿童会因好奇、因美感、因探究……凡此种种都促其形成一种关注、探究而要学。”脑科学的研究发现，“只有情绪才能为我们提供足够多的热情来达到目标”。留有“新悬念”正是从心理学与脑科学的研究角度出发，注重“把情感活动与认知活动相结合”，确保数学学习中儿童主体性的实现。

接下来，我将以《三角形的秘密》一课教学为例，与大家分享我在这方面的实践与思考。

在对苏教版四年级下册“三角形”这部分内容进行整体研究时，我发现，虽然都是在研究“三角形”，但教材对各课时内容的编排均相对独立（练习课除外），未能很好地呈现出同一主题下不同知识间的相互联系，也不利于学生数学学习的自主开展。比如，教材第二、第三课时的内容分别是“三角形的三边关系”与“三角形的内角和”，前者研究三角形的边，后者研究三角形的角，但无论是教材的编排还是我们的常规教学，给学生的感觉都是研究完边，再去研究角，这两者间似乎没有关联，只是在教材及教师的指导下听命行事。

对此，我思考，在“三角形”这个板块中，是否能为学生预留一条可以贯穿这些内容始终的线索，指引他们不断有新的感悟、新的思考、新的发现，进而围绕这些感悟、思考与发现进行一些有目的、有意义并初具主动性的数学活动呢？如果可以，想必在这样的过程中，学生会有更进一步探究的欲望，更能感受到数学思考、数学发现的乐趣，更能体验到数学本身的魅力。

经过梳理，我发现，这条线索应该就是三角形中边与角这两种元素间的紧密联系。因此，从这个板块的第一课时《认识三角形》的教学开始，我就十分注重为学生的探究留有“新悬念”，让他们在感受三角形边、角间紧密联系的同时不断有新的感悟与发现。（具体可参阅本刊2021年第1~2期《立足“高观点”，让学习在数学与儿童的和谐统一中走向深刻》）

同时，我又将“三角形的三边关系”改编为“三角形的秘密”，这里的“秘密”不仅指“三角形的三边关系”，更指学生在发现三角形的角与其对边相互关系的基础上，更多可能的发现。

关于这一内容新授部分的教学设计与思考，大家可参阅本刊2021年第5期《创设“真情境”，让学习在学与教的价值归一中走向深刻》一文。以下案例重点介绍在新授部分教学的基础上，如何为学生留有“新悬念”，引领他们持续、主动、自发地展开数学探究。

【案例】“三角形的秘密”拓展练习

师：通过刚才的探究我们发现，三角形中固定长度的两边，夹角越大，对边越长；夹角越小，对边越短。在此基础上，通过思考、交流与辨析，又发现了“三角形任意两边之和大于第三边”。接下来，让我们一起来看一道练习。

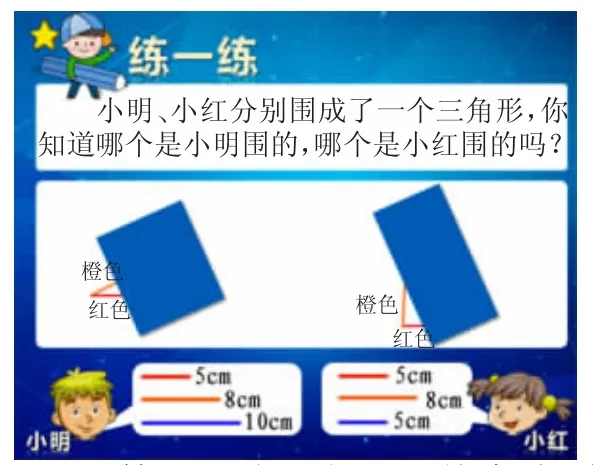
课件出示问题后，学生先独立思考，随后教师组织交流。

生：第二个三角形是小明围的，第一个是小红围的。因为我们看到的是三角形中红色与橙色这两条边的夹角，而固定长度的两边，夹角越大，对边就越长，第二个三角形中这个角更大，所以它的对边应该更长些。

师：是这样吗？大家同意他的观点吗？一起来看看。

课件移去遮挡的图形，呈现两个完整的三角形。（如图1）

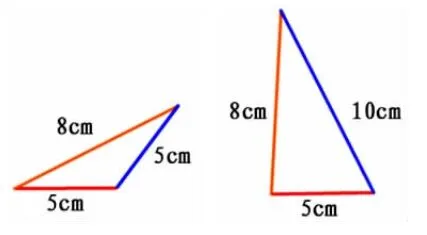
图1

师：抓住三角形边与角的关系进行分析，真棒！小丽也用三根小棒围成了一个三角形，你能想象出这个三角形的样子吗？

生：5厘米和8厘米这两条边的夹角应该比第一个三角形的这个角要大些，比第二个三角形的这个角要小一些，大致应该是这样。（边说边比划）

生：这是一个等腰三角形，因为有两条边都是8厘米。

学生交流后，课件出示答案。（如图2）

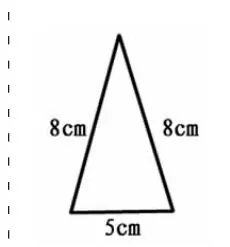
图2

师：怎么样，与你想象的一样吗？仔细观察，你还有什么新发现？

生：等腰三角形的两个底角大小相等。

师：是啊，好多同学都听说过这一点。不过，想想，为什么这两个角的大小会相等呢？与我们今天发现的秘密有关联吗？

师：小亮也围了一个三角形，他的三角形又会是什么样呢？

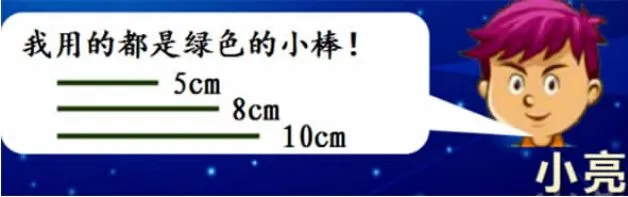
生：与小明的三角形一样，因为他用的三根小棒也是5厘米、8厘米和10厘米。

师：可能会是其他形状吗？

生：（边说边比划）不可能。大家看，如果5厘米和8厘米这两条边的夹角变了，那第三条边的长度也会变，就不可能是10厘米了。所以，只要三条边的长度相同，它们围成的三角形形状就一定相同。

师：看来，三角形的形状与它的三条边的长度密不可分。想想，这里又会藏着三角形怎样的秘密呢？

整节课中，在教师的精心设计下，为学生预留了多处可能会引发“新悬念”的空间。在这里，“三角形的秘密”既指经过探究已经发现的“秘密”，也指在探究中初步有所感悟，但还未及深入去观察、操作、思考的潜在“秘密”。

比如，在拓展练习之前的探究中，学生发现“固定长度的两边，夹角越大，对边越长……”时，如果关注到三角形的三个角，就会初步发现这个夹角越大，另外两个角就越小，而当这个夹角张到接近180°时，另两个角就越接近0°，由此引发关于“三角形内角和”的“新悬念”。

又如，上面的练习中，小丽的等腰三角形的出现，可能引发的是“等腰三角形的两个底角为什么相等？”这样的“新悬念”。对于这一点，教材是引导学生通过操作进行验证的，即把等腰三角形对折后能完全重合，说明两个底角相等。而在上面的活动中，“新悬念”的引发，则为学生预留下了以推理、思辨来进行论证的探究之路。在此基础上，学生对“三角形中，大角对大边”这一性质的发现也会成为可能。

再如，在对小亮所围的三角形形状的辨析中，为学生预留的“新悬念”是“三角形的边、角与它的形状间的紧密关联”。从学生的发言中也可看出，他们已初步触摸到“三角形的稳定性”的数学本质。

这些经过教师精心设计，为学生预留下的“新悬念”，一定会成为学生心心念念、极欲一探究竟的数学“秘密”，也一定会促发他们主动踏上揭秘的探究之旅。如此，数学的学习与研究就不再是教材与教师指引下的按部就班，而会在“悬念—发现—新悬念—新发现”的循环中不断走向主动、持久与深刻。