一种基于机相扫阵面雷达的重点目标方位角估计方法

完 诚，张 磊，钱乔龙，曹文杰，赵中兴

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

应用于区域监视的雷达，其目标探测概率及扫描周期在一定程度上相互制约，对目标的扫描积累时间越长意味着多普勒处理得到的信噪比(SNR)和杂波抑制就越好[1]。对于数字波束形成(DBF)阵面雷达，为了实现广大区域内目标的监视搜索，雷达一般工作在宽发窄收的模式下，阵面宽空域发射以满足最大探测覆盖区域，应用数字接收波束形成技术能在接收通道的同时形成多个波束，利用高重频可实现对目标的多次扫描积累，以满足较好的检测概率和杂波抑制能力。

阵面雷达的方位精度一般取决于方位波束宽度和方位量化角度。单脉冲测角可以获得很高的方位精度[2]，通过和差波束的方式，利用相位比较法或者幅度比较法精确估算目标位置，若需要工作在边扫描边跟踪的模式下，雷达阵面设计一般较为复杂[3]。本文提出一种机相扫同时方位电扫的一维相控阵体制阵面雷达。该雷达在全阵工作模式下，仅通过机扫即可对目标方位进行滑窗处理，在边监视边对重点目标跟踪的工作模式下，可以将阵面划分为2个子阵。一个子阵用于监视搜索；另一个子阵对重点目标进行跟踪，该子阵可以对重点目标在一定方位角度范围内进行多次积累探测，这样重点目标方位角的估算精度就比机相扫监视搜索的精度高得多。

文献[4]提出了一种迭代求解混合范数约束下的稀疏谱以提高估计精度，该算法在同等阵元条件下有较好的探测性能、较高精度的估计误差以及噪声子空间，但是算法计算复杂，对硬件的要求较高。在文献[5]中，假设波束形状为高斯函数，可计算出方位中心。但利用高斯函数模型处理低于半功率电平的波束时，精度就会快速下降。

本文提出了一种基于机相扫阵面雷达的比幅测角技术来实现重点目标的方位角估计，给出数字波束形成雷达表达式并介绍了幅度比较技术，阐述了波形模型以及阵面旋转时对重点目标的方位角估计方法，最后给出仿真结果。

1 数字波束形成

雷达射频前端利用数字波束形成技术，通过阵面中的阵元加权求和实现接收信号的合成。加权求和可以在特定方向实现信号积累，同时抑制其他方向的信号。假设雷达阵面天线由M个平行天线线阵组成，天线线阵均匀安装在雷达阵面中，某个点目标相对于雷达天线阵面的方位角为θ，接收时可以在几个不同角度处同时形成多个波束(如图1所示)，这些角度称为扫描角，第i个波束的扫描角用θi表示。

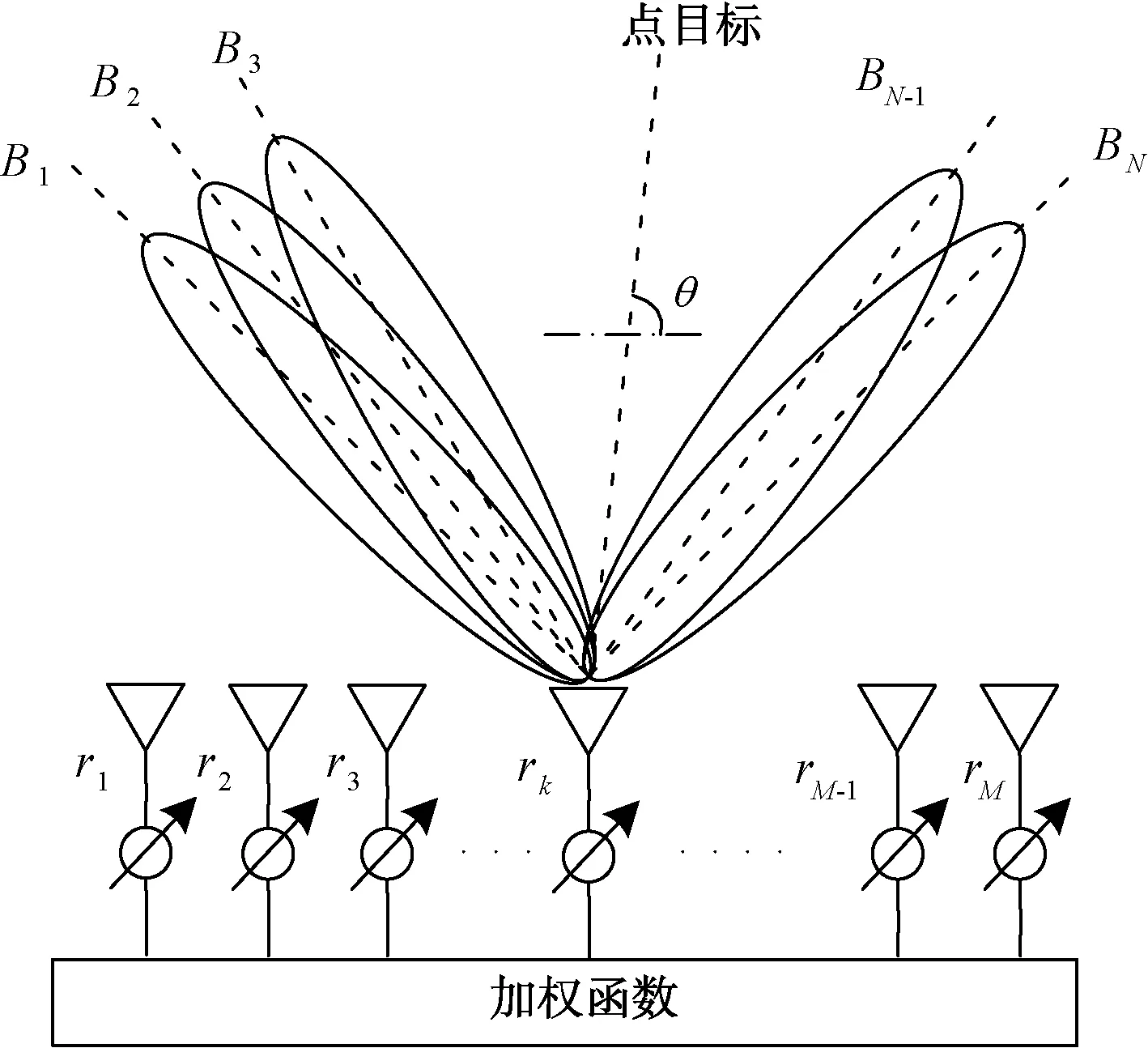
图1 数字波束形成雷达结构

假设在方位上有N个固定波束扫描角，扫描角为θi的第i个波束处的信号为Si(t)，那么第k个阵元的接收信号可表示为：

(1)

M个接收阵元信号的矢量形式为：

R(t)=B·S(t)+N(t)

(2)

式中：R(t)=[r1(t)…rM(t)]T,为各阵元接收信号组成的信号矩阵;B=[b1(θi)…bM(θi)]T,为M个阵元第i个波束角θi的扫描矢量矩阵；bk(θ)=[b(θ1)…b(θN)]，k=1，…，M；S(t)=[s1(t)…sM(t)]T，为M个阵元扫描角的信号量矩阵；N(t)=[n1(t)…nM(t)]T，为M个阵元白高斯噪声矩阵。

式(2)是接收信号的矩阵形式。调节每个阵元的加权系数可以获得波束方向图。如果加权系数组成加权函数V，那么波束形成器的输出信号表示为：

Y(t)=VHR(t)

(3)

将泰勒加权[6]用于加权函数V，波束的具体形状和位置由加权函数V确定(见图2)。

图2 泰勒加权的波束方向图

在有限的雷达阵面尺寸与处理资源及存储资源内，为了获得可接受的目标方位精度，雷达波束必须充分叠加(相邻波束间距不超过2/3个3 dB波束宽度)，若目标回波信号能够超过信号处理SNR的检测门限，则可以利用多个相邻波束对方位角进行估算。

图3为目标在3个相邻波束中的示意图，实际目标位置稍微偏向波束中心右侧，在波束中心方向图中观察到的目标强度为AC，波束右侧处的目标强度为AR，波束左侧处的为AL。从图中可以看出，在目标与右侧波束的交点，其幅度AR远低于-3 dB电平,但略大于-30 dB。因此波束建立模型至少满足AR最小值，同时雷达方位副瓣必须小于-30 dB。

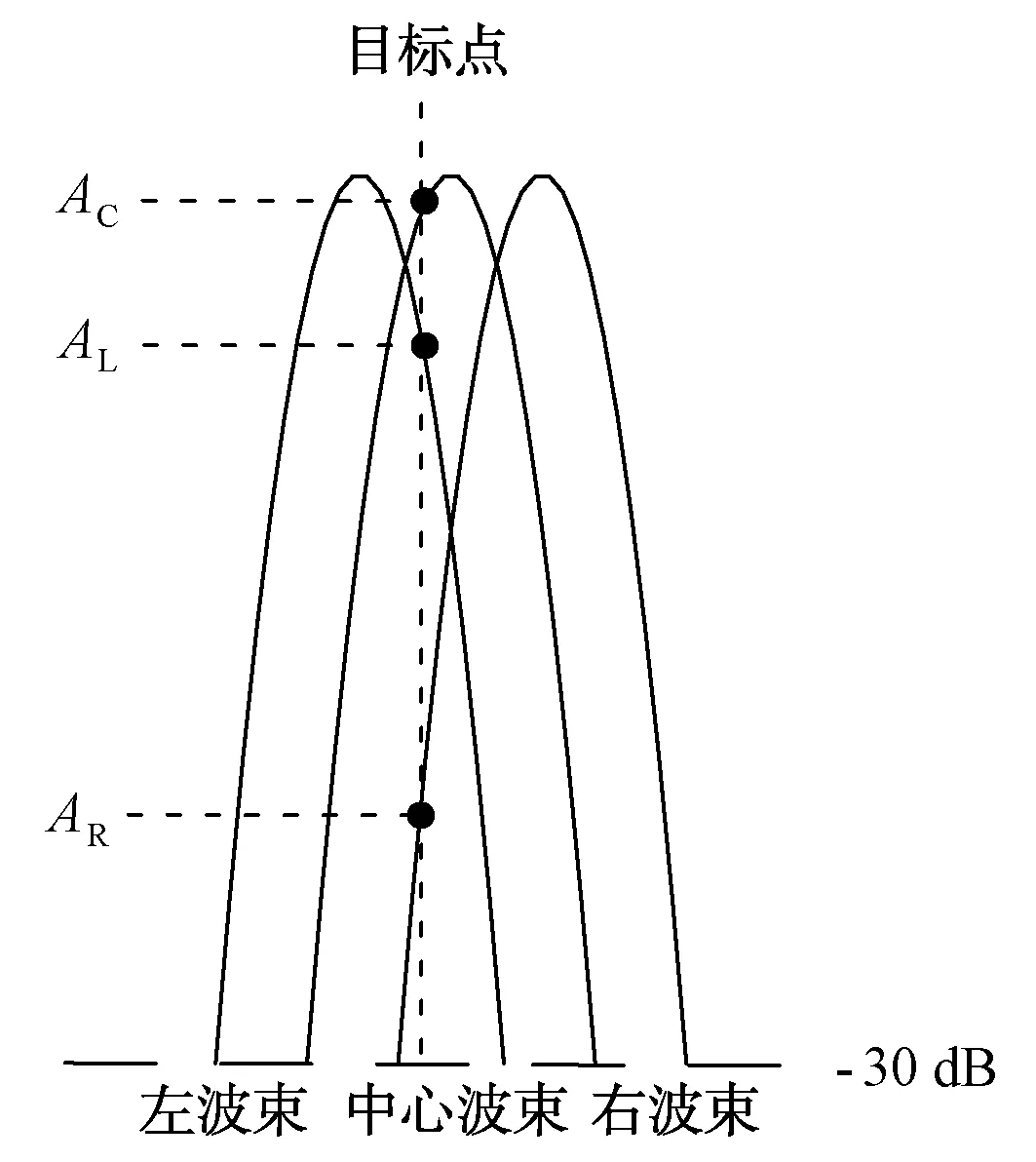
图3 多个波束中的目标探测

2 方位角估计法

2.1 多项式拟合法

由于每个扫描角处的波束形状都不同，因此要单独建立每个波束的模型，为了能够建立可用于半功率电平点之外的接收波束数学函数模型，采用多项式拟合的方法。图4为0°扫描角的波束方向图，仿真方向图中-30 dB以上的点采用0.10°的角度间隔，应用多项式拟合法得到近似波束方向图。在分析了所有扫描角处的波束形状之后，应用四阶多项式拟合近似波束形状。

图4 在0°时多项式拟合近似的波束方向图

第i个波束处的目标幅度由下面的多项式给出：

(4)

主波束和相邻波束的绝对幅度是已知的，因此角度估计值可以写成：

(5)

2.2 重点目标的方位角估计

本节阐述在机相扫阵面雷达中应用该方法对重点目标的方位角进度估计。图5、图6和图7说明了3个雷达波束中目标能量的扩展情况。

图5 中心波束的目标能量

图6 右侧波束的目标能量

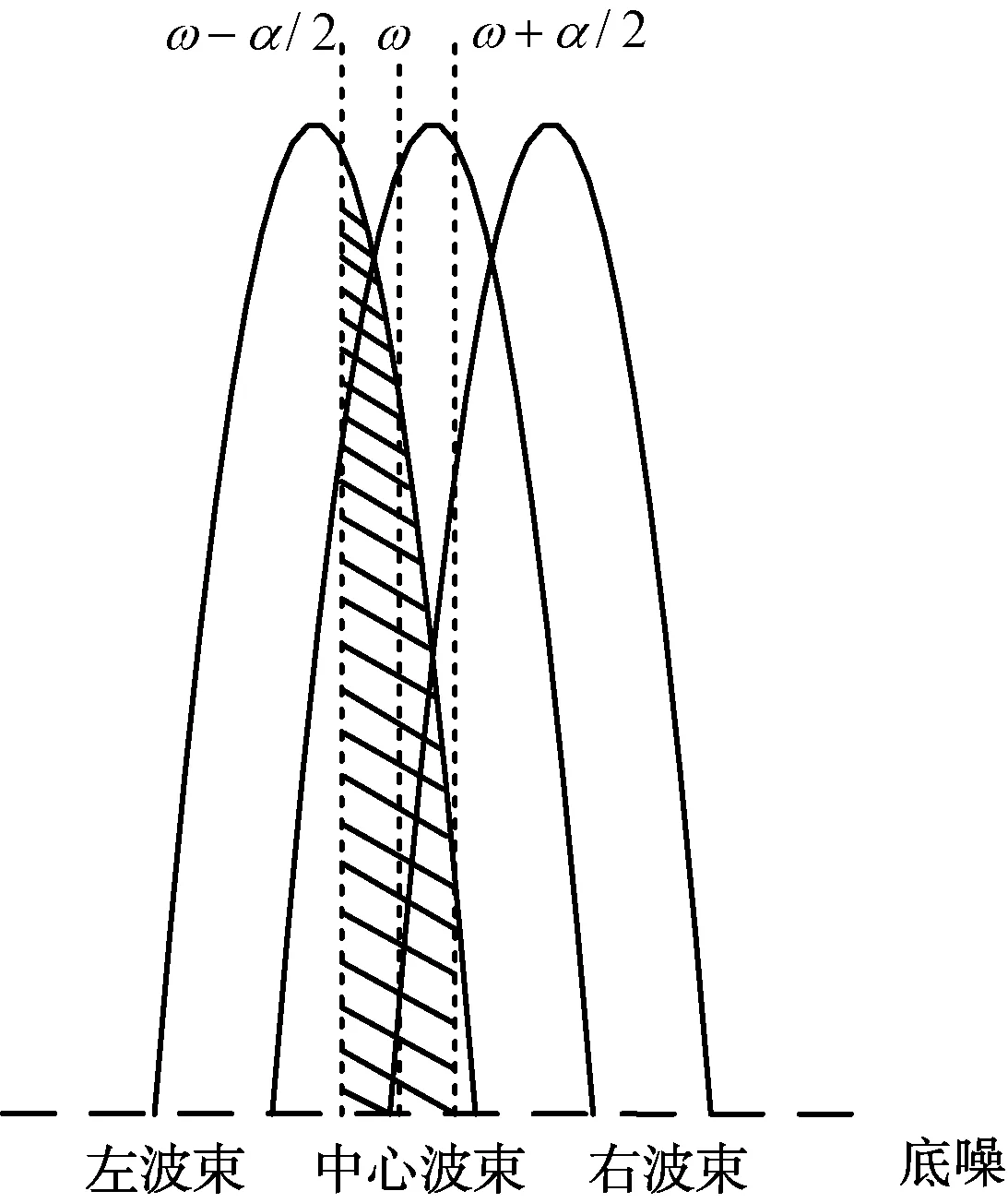
图7 左侧波束的目标能量

当目标SNR为TSNR时，第i个中心波束的多项式近似表达式为：

(6)

类似地，目标SNR为TSNR时，左侧波束(i-1)和右侧波束(i+1)的表达式为：

(7)

下面用中心波束和左侧波束计算方位中心：

(8)

用中心波束和右侧波東计算方位中心：

(9)

式中：α为角估计周期内的转动角度；ω为搜索角，ω=[θi-1,θi+1]。

如果目标是在2个以上的波束中探测到的，那么平均左侧波束和右侧波束的角度测量值就可计算出方位角：

(10)

3 仿真与分析

为了验证该方法的可行性，假设某C波段低副瓣天线阵面的方位阵元个数为32个，阵元间距为发射波长的一半，副瓣≤-30 dB，该雷达阵面的法线方向3 dB波束宽度为1.8°，方位副瓣≤-30 dB。

假设雷达不旋转，目标位于阵面法线方向，天线发射波束主瓣完全对准目标，调整目标积累前信噪比从-5 dB到15 dB，变化间隔2 dB，在不同信噪比条件下进行300次蒙特卡洛重复独立实验，对目标方位角均方根误差随信噪比的变化情况进行仿真评估，统计结果如图8所示。

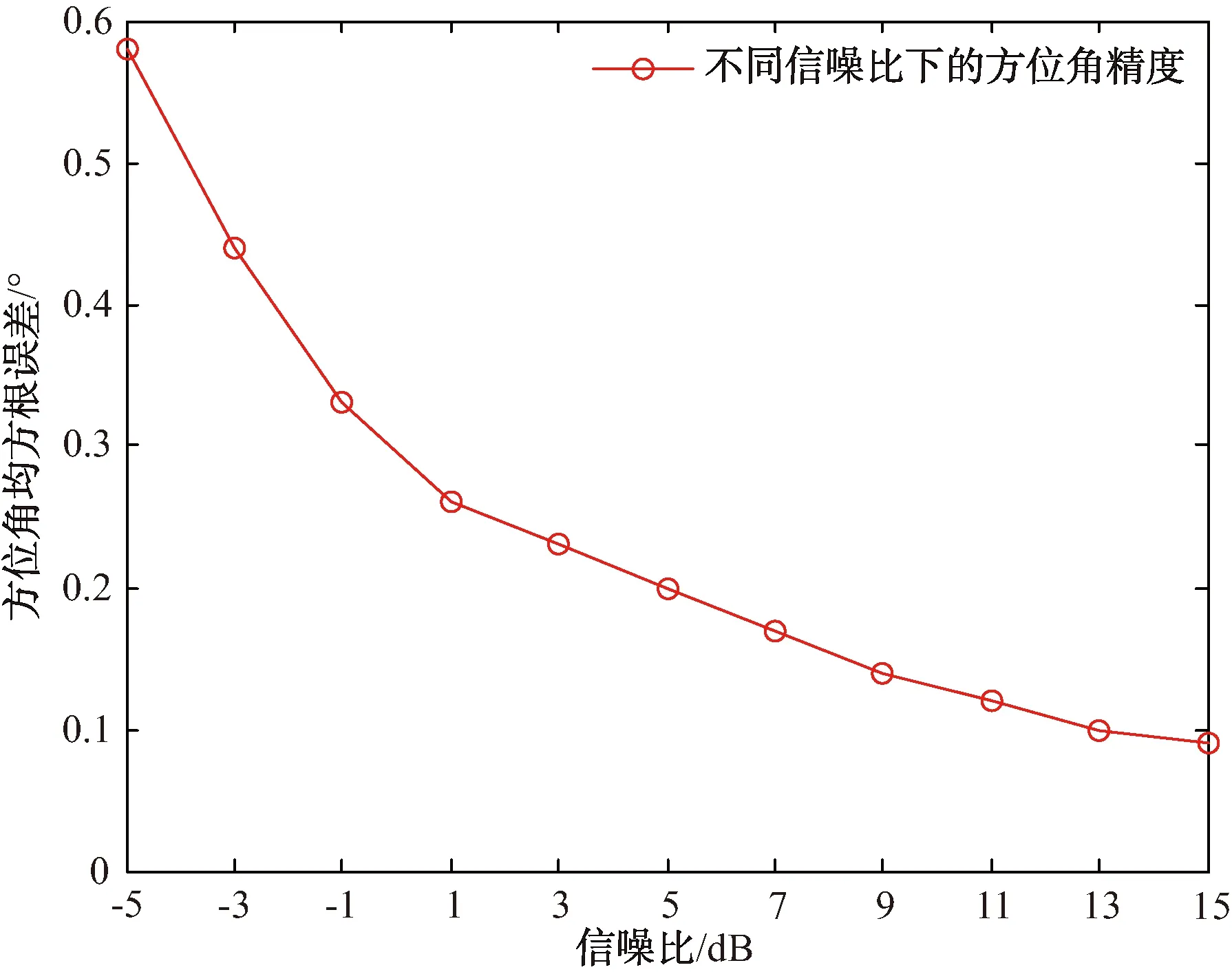
图8 不同信噪比下的方位角误差

从图8中可以看出，当目标SNR小于1 dB时，该算法下的均方根误差急剧减小，保证了强杂波区域小目标的探测能力。

雷达阵面在不旋转的情况下，模拟信噪比为10 dB的相同目标，相对雷达阵面法线不同方位处的均方根误差值，其结果如图9所示。从图9中可以看到，虽然在偏离法线方向波束宽度会相应展宽，但是雷达采用了多项式拟合近似波束形状，其方位精度变化不大。

图9 不同方位的方位角误差

为了进一步验证雷达在不同旋转速度下目标方位角精度的变化情况，假设雷达旋转速度为15°/s、30°/s以及45°/s，天线发射波束主瓣完全对准目标，调整目标的积累前信噪比从-5 dB到15 dB，变化间隔2 dB，不同信噪比和不同转速条件下进行300次蒙特卡洛重复独立实验，仿真结果如图10所示。

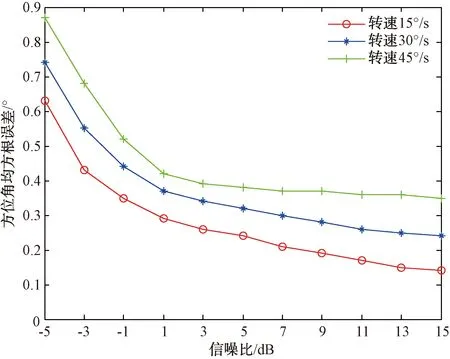
图10 不同转速下的方位角误差

从图10中可以看出，当雷达转速增大后，目标信噪比对方位精度的影响明显减弱，其方位精度主要取决于接收波束的叠加程度以及方位波束的拟合精度。当雷达转速较低时，对于SNR大于1 dB的目标，其方位精度至少可以达到0.3°。

4 结束语

本文提出了一种对监视区域内重点目标的方位角估计方法，介绍了利用多项式拟合对不同方位波束的精确建模，进而对旋转阵面应用比幅测角法实现对重点目标方位的估算，最后对该方法进行了仿真分析。