基于离散傅里叶变换的天线扫描周期测量方法
2021-09-25黄自强
黄自强
(中国电子科技集团公司第五十一研究所,上海 201802)
0 引 言
天线扫描周期是机械扫描雷达的重要特性。尤其对于大型设备,在设计确定后,一般不会进行更改;在使用过程中,也仅有少数以天线扫描周期为特征的工作模式可以选择运行。基于天线扫描周期信息通常具有较长的生命周期,可作为雷达辐射源识别的一项重要作战技术参数[1]。
扫描周期测量方法有直接法、自相关法[2]和脉冲族法[3]等。本文通过研究雷达照射持续时间内的脉冲幅度信息,提出一种新的测量方法,即基于离散傅里叶变换的频域处理方法。由于频域的信号处理方法在短波和微波等领域有较为成熟的应用,可以将成果应用于扫描周期测量领域,在一定程度上拓展了扫描周期测量领域的研究空间。
1 技术原理
简化的侦察方程如下[4]:
(1)
式中:Pt为发射功率;Pr为接收功率;Gt为发射天线增益;Gr为接收天线增益;λ为波长;R为收发距离。

Pr=GtK
(2)
发射天线方向图APt(φ),其中φ∈[0,2π);令φ=2πk+φ,其中φ∈[0,+∞),k∈Z,将APt()拓展到[0,+∞),则:
APt(2πk+φ)=APt(φ)
(3)
发射天线的扫描周期记为Tt,则发射天线的角速度wt=2π/Tt,易知ft=1/Tt,则:
Gt(φ)=APt(2πftt+φ0)
(4)
结合式(2)和(4),可得:
Pr(t)=K·APt(2πftt+φ0)
(5)
由式(5)发现Pr(t)呈现周期性变化,Pr(t)可用傅里叶级数形式表示[5]:
(6)
对于正弦信号x(t),其幅值、频率、初相为A、f0、φ0,有:
x(t)=Acos(2πf0t+φ0)
(7)
式(7)离散化后可得x(n):
(8)
因为采样和处理数据为有限长度,故对x(n)使用矩形窗g(n)截断,则信号为:
(9)
x(n)的N点离散傅里叶变换(一般采用FFT运算)记为X(k),由于实数序列FFT具有对称性,只需分析频谱X(k)的前N/2点分布情况:
(10)
式中:l0=Nf0/fs,l0为实数;l0=k0+δ0,k0为最接近l0的整数。
易知X(k)在k=k0时取得最大值。
综上所述,提取Pr(t)数据并离散化形成Pr(n),对Pr(n)进行离散傅里叶变换形成频谱X(k),寻找X(k)的最大值X(k0),则天线扫描周期为Tt=N/k0fs。
2 实现方法
具体测量方法如图1所示。
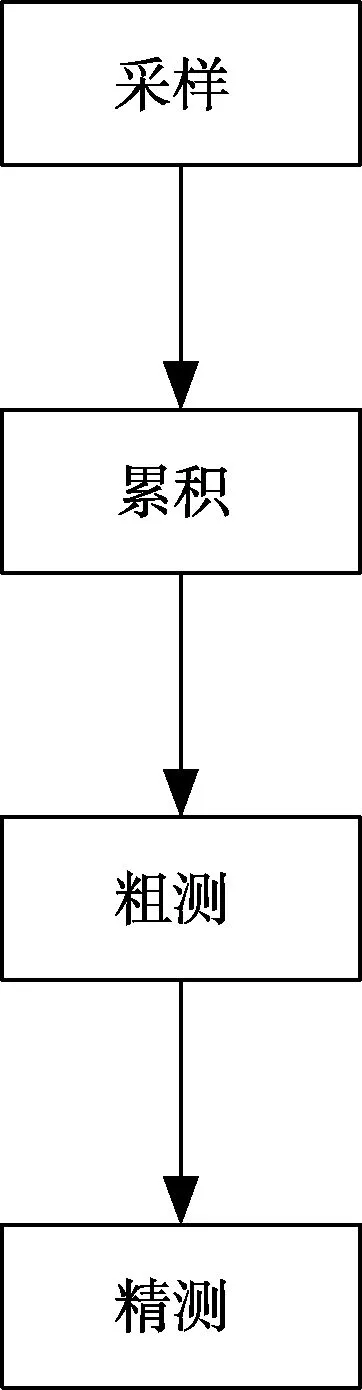
图1 测量方法流程图
2.1 采样
通过侦察设备截获发射信号,经过一系列射频处理和数字处理形成持续脉冲描述字{P0,P1,…,Pm},提取脉冲描述字中的脉冲到达时间T和脉冲幅度信息A,形成持续天线幅度描述字{B0,B1,…,Bm},其中Bm=[Tm,Am]。
采样频率fs=1/Ts,根据奈奎斯特采样定理需满足如下要求[6]:
fs≥2fh=max(ft)
(11)
对于T=kTs时刻,存在Tm≤kTs≤Tm+1,由于:
ΔTm=Tm+1-Tm≪Ts
(12)
可以认为第m个脉冲和第(m+1)个脉冲之间的幅度变化为线性,易得:
(13)
形成的采样数据为{S0,S1,…,Sk},其中Sk=[kTs,AkTs]。
2.2 累积
累积N个采样点{Sk,Sk+1,…,Sk+N-1},形成数组x(n)为:
x(n)=A(k+n)Ts=An,n=0,1,…,N-1
(14)
为方便快速傅里叶变换(FFT)运算,一般N取:
N=2p,p=0,1,2,…
(15)
FFT的频率分辨率Δf受采样时长T限制:
(16)
当采样时长T较大时,频率分辨率高;反之,频率分辨率低。需要根据实际应用情况合理选择T或N值。
2.3 粗测
求x(n)的均值,x(n)减去均值形成新的序列xa(n):
(17)
对xa(n)进行FFT运算,形成频谱X(k),寻找X(k)的最大值X(k0):
X(k0)=max{X(k)},k=0,1,…,N/2
(18)
2.4 精测
对于单频率成分或间隔较远的多频率成分的离散频谱,目前主要有比值法、能量重心法、FFT+FT连续细化傅里叶变换分析法和相位差法4种校正方法[7]。本文采用了修正Rife算法[8]对粗测频率进行校正,形成精测频率。由于具体场景对实时性要求不高,通过调整算法参数增加了运算量,提高了测频精度。
最大谱线X(k0)左右谱线分别为X(k0-1)和X(k0+1),则:
(19)
当X(k0+1)>X(k0-1)时,r=1;当X(k0+1)≤X(k0-1)时,r=-1。
当δ0较小时,则|X(k0+r)|很小,易受噪声影响;反之,最大谱线和次大谱线之间的中间区域可以保证较高的估计精度。将|X(k0)|和|X(k0+r)|频移,使得整体频移后的频率位于频移后|X1(k0)|和|X1(k0+r)|的中间区域,则:
(20)
(21)
整个过程为:根据式(19)对δ0进行估计,不满足要求则进行频移,重复上述过程,直至δ0满足要求,并进行最终校正。
3 仿真分析
设天线扫描周期转速如表1所示。

表1 天线扫描周期转速设定表
采样频率fs=0.5 Hz,N=64,假定发射天线方向图如图2所示。

图2 模拟发射天线方向图
对天线扫描周期分别为20 s、10 s和6 s,对接收信号的信噪比为20 dB、10 dB、5 dB和0 dB进行了仿真,每种情况(扫周,信噪比)进行了100次仿真,结果如表2所示。

表2 仿真结果表
通过以上仿真发现,在信噪比大于20 dB时,平均绝对百分比误差小于0.3%;在信噪比大于10 dB时,平均绝对百分比误差小于0.8%;对于相对高频的转速,每转6 s在0 dB时,平均绝对百分比误差还能小于0.8%。通过适当增加观测时间和针对性调整算法,测频精度还能进一步提高。
4 结束语
通过侦察方程和傅里叶变换的公式推导,提出了基于离散傅里叶变换的测量方法。对提出的测量方法的各个实现过程进行了分析,确定了采样、累积、粗测和精测4个主要实现步骤。在计算机仿真的基础上,通过模拟典型天线方向图、天线扫描周期、信噪比等,对一些典型情况进行了仿真分析,验证了提出的测量方法的可行性。理论分析和仿真分析表明,基于离散傅里叶变换的天线扫描周期测量方法具有广阔的研究和工程应用空间。
