计算思维素养下程序设计项目式教学探索与实践

仲轶宏

《普通高中信息技术课程标准（2017年版）》（以下简称《课标》）提倡基于项目的学习，让项目式教学在日常课堂中落地，是当前高中信息技术教师关注的热点，而计算思维是信息技术学科核心素养之一，是信息技术课堂培养学生的重要素养。如何将学科核心素养与项目式教学有效融合，将计算思维有效渗透到日常课堂教学实践中，是笔者一直探索的问题。

● 计算思维与项目式教学

1.计算思维

周以真教授认为，计算思维是一种以计算科学为核心，运用计算科学的基本概念进行问题求解、系统设计和行为理解的，涵盖计算机科学之广度的一系列思维活动。

2.项目式教学

项目式教学是随着《课标》的颁布而逐渐成为热点的教学模式，通常围绕学生生活、学习实际选取合适的项目，采用“自顶而下，逐步细化”的方法，即将完整的大项目分解成若干个小项目，再将每个小项目逐步细化、分解成一系列具体的可以实现的小任务。教师负责创设这样的真实的项目情境，在项目实施过程中以学生为主体，全程参与项目的分析、管理、求解、完善、评价等。

3.基于计算思维的项目式教学

基于计算思维的项目式教学可以理解为一种渗透式教学，它将计算思维这一学科核心素养渗透、融入到项目实施的每个环节，在计算思维的引导下推进课堂项目进度。它兼顾思维训练和课堂教学，项目随着思维的扩散而推进，思维随着项目的完善而进阶，最终使能力在思维的训练下得以提升，从而把信息技术课堂教学从重技术层面提升到重思维素养层面。

● 计算思维素养下程序设计项目式教学探索与实践

基于计算思维能力提升的程序设计项目式教学是一个较为复杂的工程。本文围绕“解决火柴棒摆数字问题”项目，开展课堂教学。该部分属于《信息技术必修1 数据与计算》中的2.4节“可以复用的代码”，旨在通过函数和模块的方法，实现代码的复用。

1.计算思维环境——创设

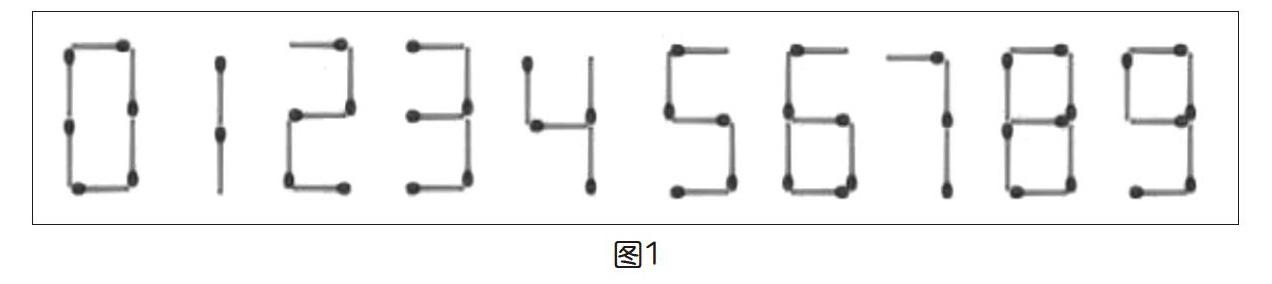
计算思维不是靠教师课堂讲解其概念、知识及方法就能形成的，它需要教师为之创设特定的内、外部环境。本课创设了“解决火柴棒摆数字问题”的Python语言程序设计的项目环境，让学生在其环境中迸发思维碰撞的火花。题目如下：已知0～9这十个数，分别由若干根火柴棒摆放而成，如下页图1所示。问题为：若给你6根火柴棒，请列出所有能摆出的自然数，要求6根火柴正好用完。

根据项目式教学中“自顶而下，逐步细化”的方法，可以对题目进行分解，把它分解成以下几个子问题：①每一个数字分别需要多少根火柴棒？②列举5个能用6根火柴棒摆出的数字？③用6根火柴棒能摆出的最大、最小数分别是多少？④一位数、两位数、三位数所需要的火柴数量分别怎样计算？依次解决这些子问题，将有助于学生找到解题思路和方法。

2.计算思维构建——求解

编程的核心是算法设计，算法即解决问题的方法和步骤，找到算法之后，还需要准确地将它通过自然语言或者流程图的方式描述出来，然后进行程序结构分析、代码编写，最后进行调试、迭代、完善，在问题求解过程中构建学生的计算思维。

如何计算一个数需要多少根火柴棒呢？即将这个数每个位上的数字所需的火柴棒数相加。那么，如何加呢？首先，让学生拆解数字如4，5，6，得出需要的火柴数为15根;其次，反推，如果给你15根火柴，能摆出哪些数字？通过拆解和摆放这一正一反的逆过程，让学生熟悉项目题意。然后根据分解的子问题，从已知条件入手，可以创建一个列表，即f=[6，2，5，5，4，5，6，3，7，6]，表达每个数字分别需要的火柴数;尝试摆出几个数字，如0，6，14，111等符合要求的数字;找到6根火柴棒能摆出的最小数0和最大数111。画出流程图，如图2所示。最后我们发现，6根火柴棒能摆出的数是[0，111]区间的部分一位数、两位数和三位数，那么将这三种类型分别找出来问题就迎刃而解了。

显然，根據列表索引及元素之间的对应关系（如下页表1），当0≤n<10时，s=f[n]，就解决了一位数问题。那么两位数呢？两位数是由十位（sw）和个位（gw）组成，思路就变成了分别取出两位数中的十位和个位上的数，通过应用整除（//）和取模（%），可得出当10≤n<100时，gw=n%10，sw=n//10，s=f[gw]+f[sw]，s即为摆出两位数中个位、十位上对应的数分别需要的火柴棒数之和。同理可类推出三位数，即当100≤n<1000时，gw=n%10，sw=n//10%10，bw=n//100，s=f[gw]+f[sw]+f[bw]，如下页表2所示。三种情况合在一起，即通过if多分支语句判断三种情况，完成一个自定义match_num（n）的函数，然后通过主程序在range（112）中判断match_num（n）==6，即可完成火柴棒摆放数字问题。

3.计算思维进阶——转变

围绕“解决火柴棒摆数字问题”的项目，笔者对项目进行升阶，把火柴数由6根改为10根，请列出所有能摆出的自然数，要求10根火柴正好用完。此时会发现，按照原来的解题思路，可以得出10根火柴能摆出的最大数是11111，此时就会涉及四位数和五位数的每位的取数问题，可以想象一个五位数将变成s=f[gw]+f[sw]+f[bw]f[qw]+f[ww]，程序将变得非常冗余复杂。显然，当火柴棒数量发生变化时，原来的算法程序已经不再适用，思维也应随之产生变化，那么，是否可以设计一个不管火柴棒怎么变，都可以适用的算法呢？

计算一个数所需的火柴棒数，即计算这个数的每个位上的数所需的火柴棒数之和，可以继续应用取模（%）和整除（//）的原理，将这个数除以10取模（n%10），求得个位数;然后将这个个位数所需的火柴棒数累加;接着去掉个位数，即将这个数对10取整（n//10）;重复以上步骤直到这个数为0。以数字12345为例，如表3所示，通过while语句循环5次，便可完成这个五位数每位的取数，然后判断这些位上的数所需的火柴棒数之和是否等于10，便可完成问题的求解，而且似乎不再受火柴棒数量的牵制。这种方法可行吗？可通过流程图来验证，如上页图3所示。

4.计算思维回归——严选

算法的改变，是计算思维变化的结果，两者互为因果关系。严谨的思维和算法设计，是程序编写的前提。再次围绕“解决火柴棒摆数字问题”，把火柴数由刚才的10根改回6根，以验证程序的严谨性。通过修改程序、调试运行，可以发现10根火柴棒摆数字完全正确的程序，火柴棒改回6根后，运行结果少了一个数0。此时，思维再次回归到刚才的算法设计上，重新思考算法的严谨性，不难发现上述算法中while循环语句的前提是n>0，即忽略了考虑n=0的问题，而10根火柴不可能摆出0这个数，故而在10根火柴棒摆数字没有出现问题，在改回6根后却出现了问题。改变思维，完善算法，堵住0这个漏洞，通过添加一个if判断分支，即当n=0时，s=f[0]，否则s=0，便可达到程序的优化。

围绕“解决火柴棒摆数字问题”的项目，解题的终点是摆出每个符合要求的数。选择if分支结构语句解题，思路清晰，便于理解，但对于数据量大、程序冗长时却不相适应;而选择while循环结构语句解题，显然更适合复杂的情况，但需要前瞻的大局观和缜密的计算思维，这也是程序算法设计的精髓。

5.计算思维升华——共享

在互联网时代，信息共享已经成为一种常态。自己编写的程序代码也可以帮到其他人，如把自己编写的“火柴棒摆数字问题”的代码成果共享给其他人。那么如何把自己的代码共享给别人呢？笔者展示了一个近似火柴棒摆数字问题的主程序的简短程序，运行后却能得到相同的结果，而且任意修改火柴棒数量，都能运行出正确的结果，如上页图4所示。这里的谜出现在程序开头的第一句“import ZYH”，ZYH是笔者姓名的首字母。有学生思维敏捷，也用自己的名字给程序加了一句，但却没有出现想要的结果，顿时陷入疑惑。解开ZYH这个谜团，便能化解学生的疑惑。ZYH是笔者自己命名的模块名，“import ZYH”就是导入ZYH这个模块。其实它的本质是把自己编写的程序代码封装进去，需要用的时候首先利用import导入模块，然后调用模块中的函数，如要实现火柴棒摆数字问题，便可通过ZYH.match_num（），调用ZYH模块中自定义函数的matchnum（）。同时，也可以把其他自定义的函数一起封装进去，ZYH.*即可调用该模块下任意函数。打开展示ZYH模块的内容，如上页图5所示。最后，把封装好的模块，构建发布文件，以崭新的维度，实现思维的升华，完成成果共享。

● 结束语

伴随着大数据、人工智能等技术的飞速发展，计算思维为学生打开了看世界的新视角，提供了解决问题的新思路，它也是今后适应社会的关键能力。教育是慢的艺术，学生计算思维的形成不是一蹴而就的，它需要在教学实践中，不断地渗透、培养。探索在项目式教学过程中渗透、培养学生的计算思维素养，不仅使思维训练有了具体的依托，而且丰富了项目式教学的内涵。尤其是在程序设计项目式教学中，从实际问题出发，分析问题，从形成抽象到简单数据模型，从算法设计到程序编写，从代码调试到优化完善程序，整个过程都伴随着思维的变化与挑战，有助于不断训练和提升学生的计算思维，使其养成良好的思维习惯，也为项目式教学从思维方法的高度培养学生做了有益尝试。

参考文獻：

[1]杨简云.基于计算思维的项目教学法在高中信息技术教学中的实践[J].课程改革与教学研究，2020（05）：35-38+44.

[2]薛磊，孙玉强，顾晓清.基于计算思维的项目教学法的研究与实践[J].职业与教育，2012（11）：148-150.

[3]张勇.基于计算思维培养的小学信息技术教学策略探究[J].中小学电教，2021（02）：95-97.

[4]王荣良.计算思维的教学评价方法探析[J].中国信息技术教育，2020（15）：56-60.

[5]韩晶.计算机基础教学中学生计算思维能力的培养分析[J].科技经济导刊，2019（17）：176-177.