把握起点,任务驱动直至思维外显
2021-09-24张琦
张琦

[摘 要]以四年级下册数学广角——“鸡兔同笼”问题为例,探究如何把握学生的学习起点,实施任务驱动策略,让学生掌握解决问题的真正策略,建立解题模型,提升思维深度。
[关键词]鸡兔同笼;起点;任务;核心素养;思维
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)23-0023-02
教师教学时常常遇到这样的情况:教学例题时學生都会,一到要学生自己动手解题时总有人不会。改作业时,常常听到教师抱怨:“这个知识点讲了多少遍了,怎么还有人错啊?”习题讲评时,常常能听到学生无奈地说:“这些知识点老师一讲我知道了,可是我自己怎样就想不起来呢?”
出现这些情况,究其原因,就是学生对学习的知识不理解,或者记住了但不会用,学习过程中只能依样画葫芦进行模仿。根据布鲁姆的认知学习过程,这属于记忆、理解、应用的低阶思维中的最底层,显然学习效果低下。如何让学生的学习从低阶思维向高阶思维转变?如何使学生的学习向分析、评价、创造迈进,让学生的学习更有深度、更有广度?笔者认为可以从以下三方面入手。
一、现实起点和逻辑起点的深度挖掘
“鸡兔同笼”一课在小学阶段属于一节“熟课”,而且也正因为是“熟课”,很多教师都喜欢挑这节课当公开课,学生或多或少都对此有所了解。但也正是由于过熟、过于出名,所以起点并不好把握。
首先,教材的逻辑起点。人教版教材将本节内容放在四年级下册的“数学广角”中进行教学,教材中列举了两种方法:列表法、假设法。用列表的方法解决问题,在三年级的方案的设计中已经有所涉及,学生并不陌生。而对于用假设法来解决问题,以往的教学并没有真正涉及。仔细分析教材中用假设法的解题思路:
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
(1)假如笼子里都是鸡,那么就有8×2=16(只)脚,这样就多出了26-16=10(只)脚。
(2)1只兔比1只鸡多2只脚,因此有10÷2=5(只)兔。
(3)所以笼子里有3只鸡,5只兔。
虽然看到的只有3个序号,但仔细观察就可以发现,实际上包含着5步计算。
第一步:假设全都是鸡,那么就有8×2=16(只)脚。
第二步:多出了26-16=10(只)脚。
第三步:1只兔比1只鸡多4-2=2(只)脚。
第四步:10只脚里包含着几个多出的2只脚,就有几只兔,即10÷2=5(只)兔。
第五步:8-5=3(只)鸡。
5步计算解决问题,学生在四年级以前很少接触到,而且除了第五步数量关系很明确以外,其他4步都和解决问题没有直接的联系,导致学生只能模仿着记忆。
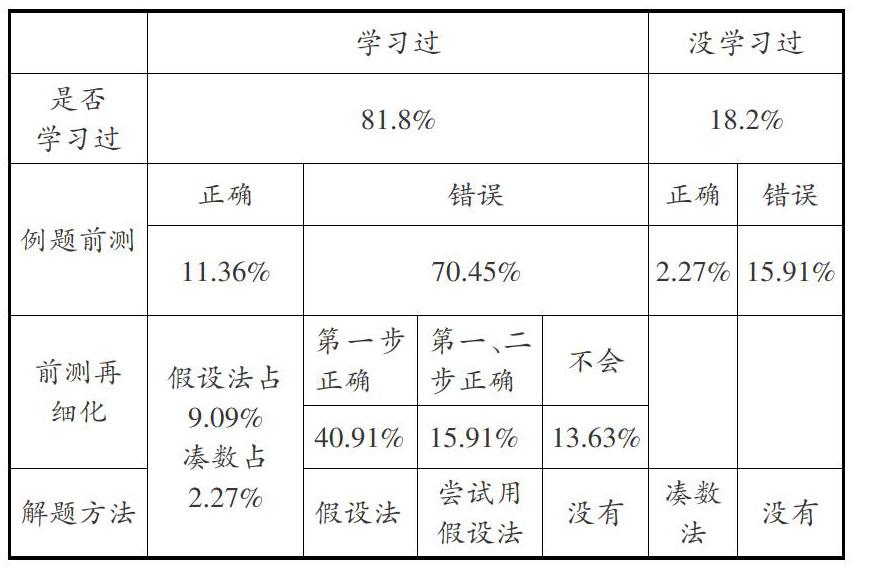
再看现实起点。以学校一个班作为样本从3个维度进行问卷分析,具体数据如下:
从表中可以看出,虽然很多学生已经接触或者学习过“鸡兔同笼”的内容,但实际效果并不能让人满意,56.82%的学生凭借着模糊的记忆去解题,显然达不到理解应用的程度。
面对这样的前测结果,笔者可以肯定,学生对“鸡兔同笼”问题的前期浅层次的接触,在一定程度上影响了学生的探究思维,学生凭借以前的模糊记忆或者解题方法硬性拼凑,导致错误率高。
根据对学生学习起点的深度挖掘,结合学生学习的逻辑路径,笔者得出两个教学思路:第一,淡化“鸡兔同笼”情境,设计与学生生活实际相联系的学习情境激发学生的学习兴趣;第二,给学生的学习路径搭建一个有以往经验的模型。基于此,笔者教学时将教材中的情境改为组装玩具小车:
学校车模小组组装三轮和四轮小赛车,要组装12辆,最多要几个轮子?最少要几个轮子?一共有几种可能?
这样的设计不仅将学生以前关于租车方案设计的经历结合起来,而且在一个相对开放的情境中,使学生可以打破原来记忆中“鸡兔同笼”的思维定式,为学生的探究提供基础保障。
二、层层驱动促使深度探究
任务驱动是深度探究的重要保障和核心要素,有趣味性和挑战性,就近发展区的任务驱动更能激发学生探究的兴趣,让学生沉浸其中并获得成功的体验。
第一层任务驱动:组装玩具小车。有以往设计租车方案的经验基础,学生会从最多或者最少的角度出发进行探究,问题解决的策略呈现出多样性。
多样的解题策略为不同层次的学生提供了不同的探究方式,满足了学生共性与个性的需求。
第二层任务驱动:观察刚才探究中组装玩具小车的所有可能,你能将这些可能有序排列吗?
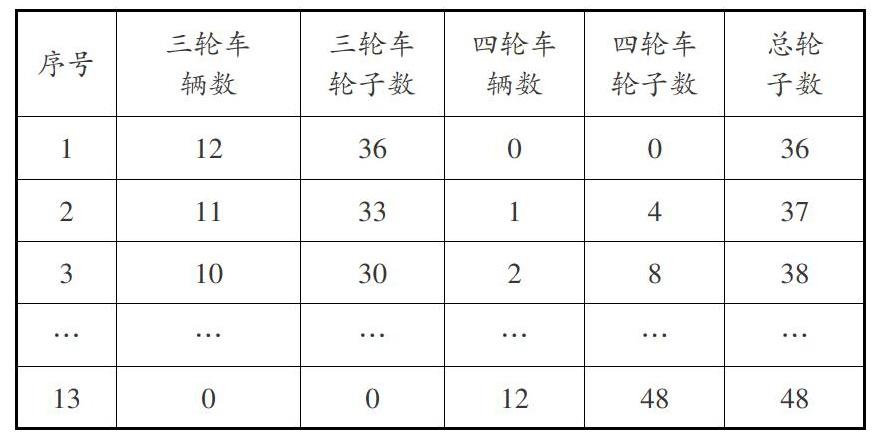
将所有可能有序排列,最直观的方法就是列表,在这样的任务驱动下,促使其他几种解题策略与列表的方法进行融合与有序统整,最后得出下表。
第三层任务驱动:从表格中你发现了什么变化规律?思维层次不同的学生得到的结论也不同,从最初的三轮车数量逐一减少,四轮车数量逐一增加,逐渐探究到每减少1辆三轮车、增加1辆四轮车,总轮子数就会多1,这个“1”就是1辆四轮车比1辆三轮车多的1个轮子。在不同层次的表达中,学生的思维不断完善、不断提升。
第四层任务驱动:如果现在组装12辆车用了40个轮子,利用刚才的规律,你能根据第一种方案一下子就想到三轮车的数量和四轮车的数量吗?说说你是怎样想的。这个过程你能用算式表示出来吗?
12×3=36(个)
40-36=4(个),4-3=1(个)
4÷1=4(辆)四轮车
12-4=8(辆)三轮车
从案例中可以看出,从第一层任务驱动写出所有可能如何将可能有序排列发现规律、利用规律,回归算式。任务驱动层层递进,每一层任务都给了学生探究的空间。学生可以通过“学共体”,共同进行深度探究,找到规律以及知识点之间的共性,真正理解假设法解决“鸡兔同笼”问题的策略。
三、建模中提炼深度思维深度
一道题的解决并不意味着学生对“鸡兔同笼”问题的理解就十分深刻了,还需要通过更多同种类型的问题去引导学生从一道题走向一类题。
第一步“辨”。出示问题:“鸡兔同笼”问题和“40个轮子组装三轮车和四轮车共12辆,有几辆三轮车,几辆四轮车?”这个问题有什么相同之处和不同之处?学生在对比中可以慢慢发现,其实这两个问题都是同一种类型。相同之处在于,车辆的总数相当于头的总数,轮子的总数相当于脚的总数;不同之处在于,1辆三轮车与1辆四轮车只相差1个轮子,而1只鸡和1只兔相差2只脚。
第二步“练”。除了辨别异同之外,更直观的是让学生能自己解决“鸡兔同笼”问题,放手让学生进行练习,针对学生学习水平的不同,可以让他们用不同的解题方法来解决这类问题,比如列表法、画图法和列算式法,并说说这些方法的优劣。
第三步“归”。无论用哪种方法,说说用这几种方法的共性是什么?无论哪种方法,都用到了假设这一方法。
深度学习是师生共同经历的一场智慧之旅,旅程的目的是走向核心素养。在关注终点的同时,教师还应该关注旅程的过程,让学生经历积极、深入地去思辨、去验证、去探索的思维过程,使得学习走向深度。
(责编 吴美玲)
