基于IFAHP-TOPSIS方法的控制系统执行器风险评估

张文广， 沈炀智， 李浩瀚， 袁桂丽

(1．华北电力大学 新能源电力系统国家重点实验室，北京 102206；2．华北电力大学 控制与计算机工程学院，北京 102206)

自动控制技术被广泛应用于电力、航空航天和化工等领域[1]，由于现代控制系统规模和复杂程度日益提高，系统发生故障的可能性也增加[2]。根据故障发生位置的不同，控制系统故障可分为执行器故障、传感器故障、控制器故障和被控对象故障等。其中，执行器是控制系统中唯一的运动元件，如果执行器故障未被及时处理，会严重影响控制系统的工作性能[3-4]。因此，需提高执行器故障诊断技术水平。不同故障模式对系统造成的影响程度不同，其中序位前20%故障模式造成的危害程度占所有故障模式的80%以上[5]。因此，需要对执行器不同故障模式进行风险评估，以确定序位较高的故障模式。

风险评估属于综合评价范畴，综合评价包括评估指标体系构建、评估指标赋权、数学模型建立和评价方案量化等环节，目前国内外学者围绕综合评价方法进行了大量的研究工作[6]。李毅佳等[7]在传统故障模式及影响分析(FMEA)方法的基础上引入模糊理论，根据模糊风险优先度数值(FRPN)对海底管道建造期的质量进行了风险评估。杨小彬等[8]基于层次分析法(AHP)建立了配电网能效指标体系，确定了各单项指标权重，验证了指标体系的有效性和实效性。刘自发等[9]通过用5/5-9/1标度取代1-9标度来改进AHP，提高了所求权重的合理性。谭吉玉等[10]将逼近理想解排序(TOPSIS)方法与区间直觉模糊数相结合，提出了一种新的综合评价方法。Prakash等[11]将传统AHP与TOPSIS方法相结合，并对印度电子工业中的物流方案进行综合评价，消除了评价过程中主、客观因素的影响。

上述评价方法在各自工程领域均取得了一定效果，但也存在不足。笔者以控制系统执行器为研究对象，根据AHP，基于传统FMEA方法建立风险评估指标体系，构建故障序位层次结构模型；然后将改进模糊层次分析法(IFAHP)与熵权法进行动态组合，计算出风险评估指标的复合权重；运用改进的模糊逼近理想解排序(IFTOPSIS)方法得到各故障模式的最终序位；最后通过典型算例对所提出的改进模糊层次分析与逼近理想解排序相结合的方法(IFAHP-TOPSIS方法)进行验证。

1 执行器风险评估指标体系构建

按照驱动执行器的能源形式，可以将执行器分为气动、电动与液压执行器三大类。由于气动执行器具有结构简单、价格低廉等优点，较其他类型执行器应用更为广泛[12]，因此以气动执行器为研究对象进行风险评估。表1给出了气动执行器典型故障模式及对应编号。

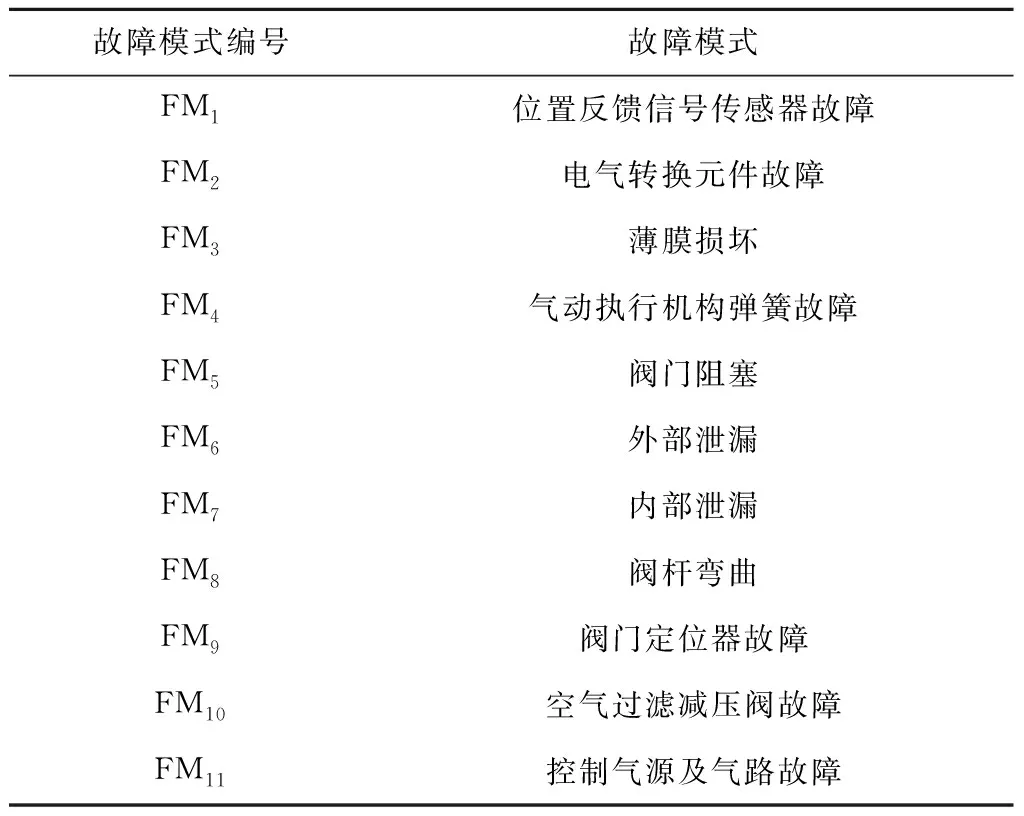
表1 气动执行器典型故障模式

为便于实际应用，需对风险评估指标进行简化统一[13]。传统FMEA方法通过计算风险因子得到相应的风险顺序数值(RPN)，从而对故障模式进行评估[14]。因此，笔者根据传统AHP的基本原理，以气动执行器故障序位为目标，分解得到2个准则层，从而建立风险评估指标体系，共计3个一级风险评估指标和6个二级风险评估指标，见表2。

表2 执行器风险评估指标

将表1中的典型故障模式作为方案层，构建控制系统气动执行器故障序位层次结构模型，见图1。

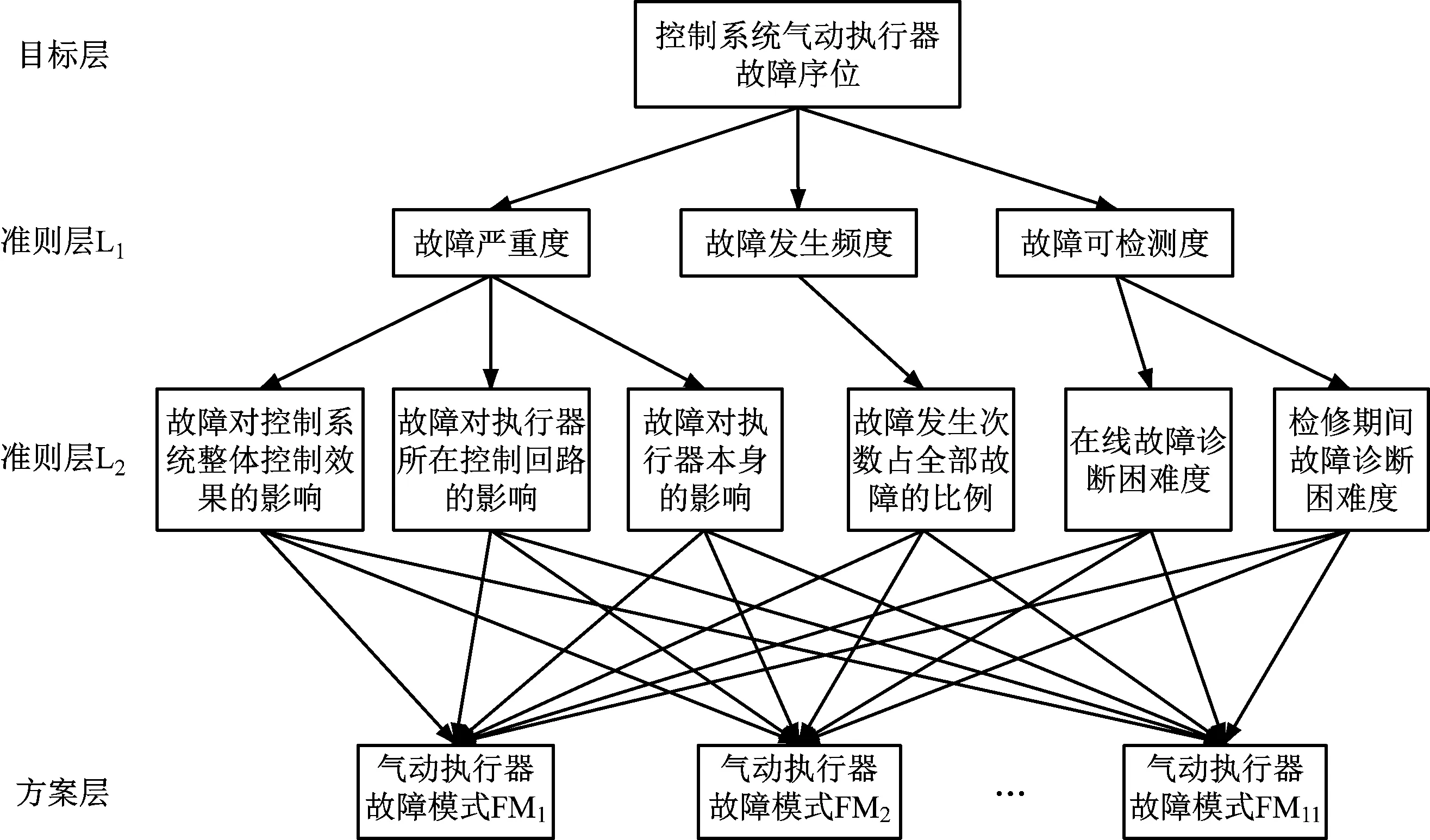
图1 控制系统气动执行器故障序位层次结构模型Fig.1 Hierarchical structure model of pneumatic actuator fault sequence in control system

2 IFAHP-TOPSIS方法

建立控制系统执行器风险评估指标体系后，基于模糊理论，将传统AHP中优先判断矩阵转换成模糊一致性判断矩阵，提出IFAHP；然后采用动态权重偏好系数代替传统组合赋权法中的固定权重偏好系数，将改进AHP与熵权法动态结合，计算风险评估指标的复合权重；最后，在传统TOPSIS方法中引入三角模糊数，并改进距离计算公式，提出IFTOPSIS方法，得到最终故障序位。

2.1 IFAHP

针对表2所建立的气动执行器风险评估指标体系，运用AHP求取指标权重[9]。IFAHP步骤如下。

步骤1：根据层次结构，构建优先判断矩阵A，用0.1-0.9标度代替1-9标度，对准则层中的风险评估指标进行两两比较。

(1)

式中：n为准则层中风险评估指标的个数；aij为风险评估指标i相比风险评估指标j的重要度，取值范围为0.1～0.9。

0.1-0.9标度法及其定义见表3。

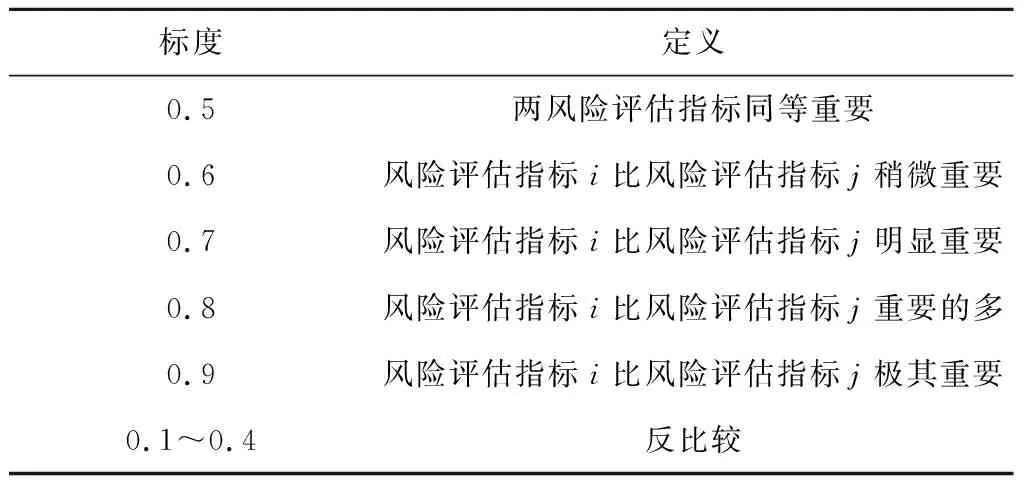
表3 0.1-0.9标度法及其定义

步骤2：优先判断矩阵A中元素满足aij+aji=1，对其中元素进行数学变换,将其转换为模糊一致性判断矩阵。

(2)

(3)

式中：ri为优先判断矩阵A中第i行元素之和,i=1,2,…,n;rij为模糊一致性判断矩阵R中第i行第j列的元素。

由此，将优先判断矩阵A转化为模糊一致性判断矩阵R=[rij]n×n，且R满足一致性条件，无需对其进行一致性检验。

步骤3：利用转换公式eij=rij/rji将矩阵R转化为互反型矩阵E=[eij]n×n。

步骤4：由方根法求取准则层下各风险评估指标的层次单排序权重向量。

计算互反型矩阵E每行元素的乘积Ei。

(4)

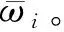
(5)

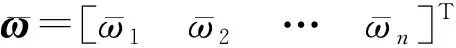
(6)

则ω=[ω1ω2…ωn]T即为所求的权重向量。

步骤5：计算层次总排序权重。

设层次结构模型中准则层L1包含m个评估指标(L11，L12，…，L1m)，层次单排序权重为ω11，ω12，…，ω1m；其下一准则层L2包含n个评估指标(L21，L22，…，L2n)，相对于层次指标L1j的层次单排序权重为f1j，f2j，…，fnj(j=1,2,…,m)；准则层L2中第i个指标相对于目标层的层次总排序权重w2i为

(7)

使用上述方法还可确定评分专家的AHP权重。

2.2 主、客观动态组合赋权法的风险评估指标复合权重

通常风险评估指标会同时存在定性和定量指标[15]。按照权重产生方法，可分为主观赋权法和客观赋权法两大类。AHP作为主观赋权法，充分考虑了评分专家的主观意愿，适用于求取定性指标权重。但是，对定量指标进行赋权时，AHP未考虑风险评估指标本身的信息，存在主观性。熵权法作为客观赋权法，能够充分利用原始数据，根据决策矩阵数据特点求取风险评估指标权重[16]。

传统组合赋权法采用固定权重偏好系数，将主观和客观赋权法所得权重结合，但由于不同评估指标偏向于定性或定量指标的程度不同，固定权重偏好系数不能体现评估指标本身的性质。为兼顾主观意愿和客观信息，将AHP与熵权法相结合，用动态权重偏好系数代替组合赋权法中的固定权重偏好系数，根据评估指标本身性质确定相应的权重偏好系数，形成主、客观动态组合赋权法，求取风险评估指标复合权重。

步骤1：由IFAHP求取AHP的权重。

步骤2：利用熵权法求权。根据标准化决策矩阵V计算熵Hj。

(8)

式中：Hj为第j个风险评估指标的熵，j=1,2,…,n；K为熵值常系数；vij为标准化决策矩阵V中的元素。

第j个风险评估指标的熵权θj为

(9)

步骤3：复合权重计算。用动态权重偏好系数代替固定权重偏好系数，以距离指标ρ作为最终的复合权重。

结合AHP权重ωj和熵权法权重θj，第j个风险评估指标的复合权重ρj可表示为

(10)

(11)

式中：εj为动态权重偏好系数。

2.3 IFTOPSIS方法

根据群决策基本假设[17]可知，风险评估质量与所用评价方法有关。TOPSIS方法是一种综合评价方法[18]，被广泛应用于评价决策领域。TOPSIS方法也需要构建标准化决策矩阵，与熵权法求取权重过程相似。为保证风险评估方法的全面性，采用TOPSIS方法进行故障排序。在排序过程中，引入三角模糊数处理不确定因素并改进距离计算公式，得到IFTOPSIS方法。基于IFTOPSIS方法的故障排序步骤如下。

步骤1：求取标准化决策矩阵。

(1) 构建模糊决策矩阵

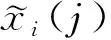
(12)

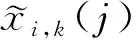
(13)

(2) 规范化模糊决策矩阵

依据风险评估指标的不同属性，共有3种模糊决策矩阵[20]，即效益型、成本型和偏离型，其中效益型模糊决策矩阵中随着风险评估指标的增加，序位升高。由于传统FMEA方法中风险因子S、O和D均为效益型风险评估指标，所以采用效益型模糊决策矩阵的规范化方法。

(14)

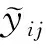
(15)

步骤2：由标准化决策矩阵中的元素确定正、负理想解。

(16)

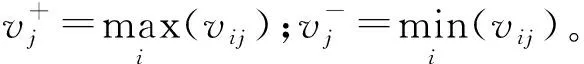
步骤3：计算故障模式与正、负理想解的距离。

采用传统TOPSIS方法计算最终序位时，其风险评估指标权重改变了原决策数据间的关系结构，导致出现逆序问题。根据权重所致逆序问题消除方法[21]，对TOPSIS方法的距离计算公式进行改进。

(17)

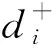
步骤4：计算故障模式FMi的相对贴近度Cl,i。

(18)

3 应用案例

采用IFAHP-TOPSIS方法对某燃气轮机电厂的气动执行器进行风险评估，并与文献[11]中的AHP-TOPSIS方法进行比较。

3.1 AHP权重

邀请5名专家(TM1～TM5)对表2中风险评估指标的相对重要性进行打分，得到各级风险评估指标及评分专家的优先判断矩阵A，其元素取值见表4～表7。根据以上优先判断矩阵，采用IFAHP计算得到二级风险评估指标和评分专家的AHP权重，见表8和表9。

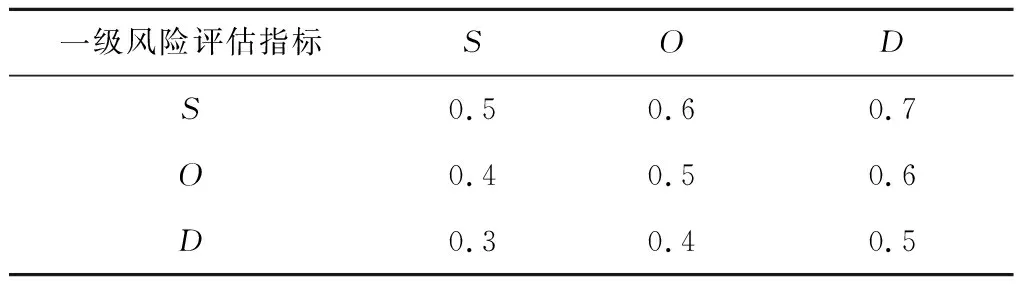
表4 一级风险评估指标优先判断矩阵中的元素取值

表5 二级风险评估指标(S)优先判断矩阵中的元素取值

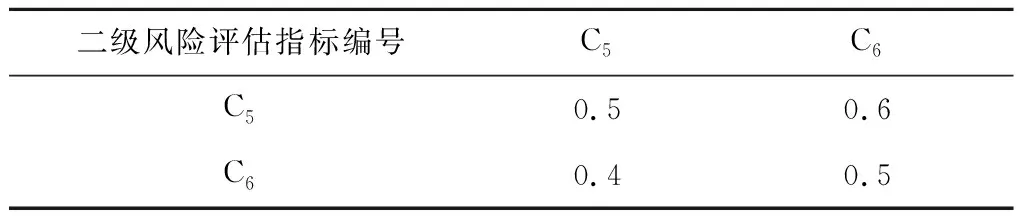
表6 二级风险评估指标(D)优先判断矩阵中的元素取值

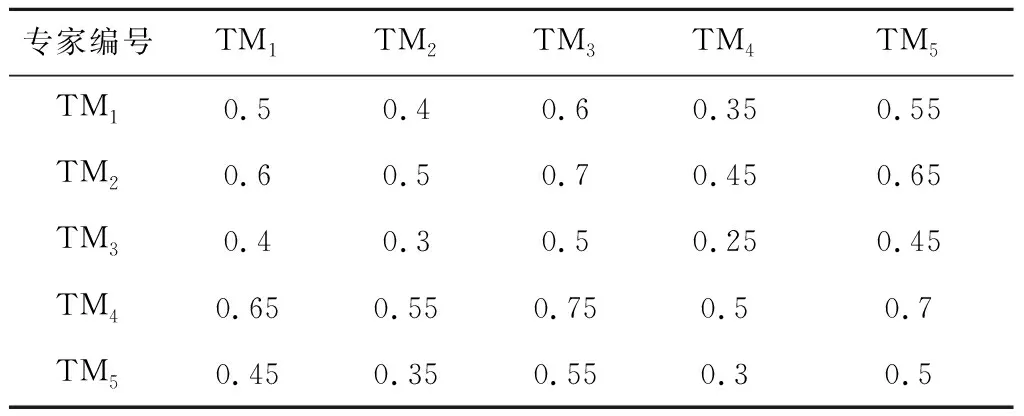
表7 评分专家优先判断矩阵中的元素取值

表8 二级风险评估指标的AHP权重

表9 评分专家的AHP权重

3.2 复合权重

表10和表11分别为风险评估指标的熵权法权重和复合权重。

表10 二级风险评估指标的熵权法权重

表11 二级风险评估指标的复合权重

3.3 故障排序

针对所有故障模式，以二级风险评估指标为基准进行模糊评价，得到模糊决策矩阵，其元素取值见表12。对模糊决策矩阵进行规范化和归一化处理，得到标准化决策矩阵，其元素取值见表13。

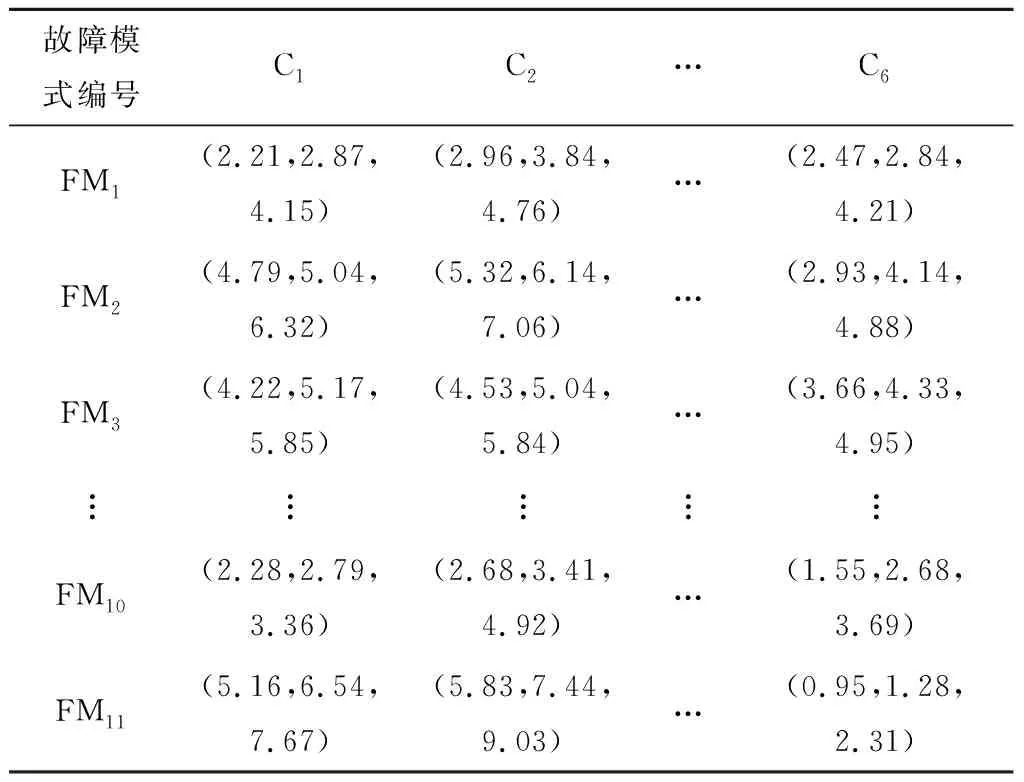
表12 故障模式的模糊决策矩阵中的元素取值

表13 故障模式的标准化决策矩阵中的元素取值

在确定正、负理想解后，采用改进的距离公式计算得到所有故障模式与正、负理想解之间的距离，见表14。基于IFAHP-TOPSIS和AHP-TOPSIS方法的故障模式相对贴近度见表15。

表14 故障模式与正、负理想解之间的距离

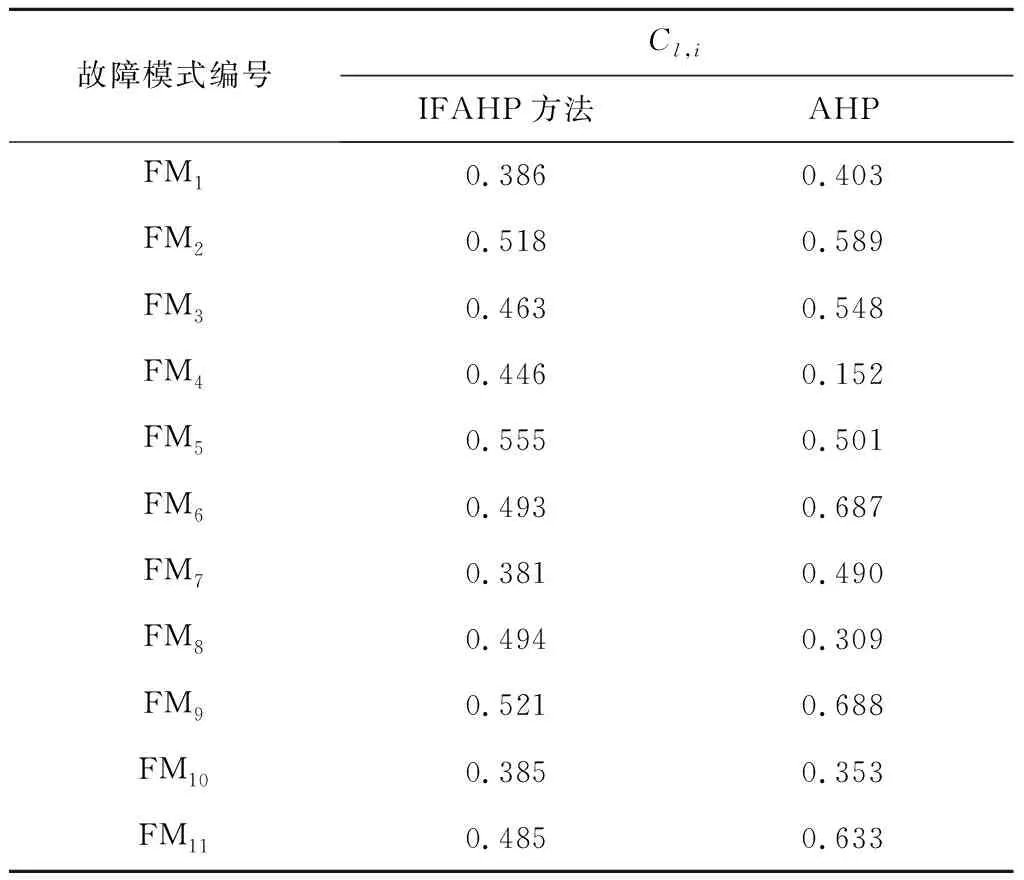
表15 基于IFAHP-TOPSIS和AHP-TOPSIS方法的故障模式相对贴近度

3.4 结果分析

在IFAHP-TOPSIS方法和AHP-TOPSIS方法下不同故障模式的序位对比见图2。从图2可以看出，基于2种方法的排序结果总体趋势大致相同，但个别故障模式排序结果差别较大。这主要是因为在利用这2种方法进行风险评估的过程中对风险评估指标权重分配不同(见图3)。

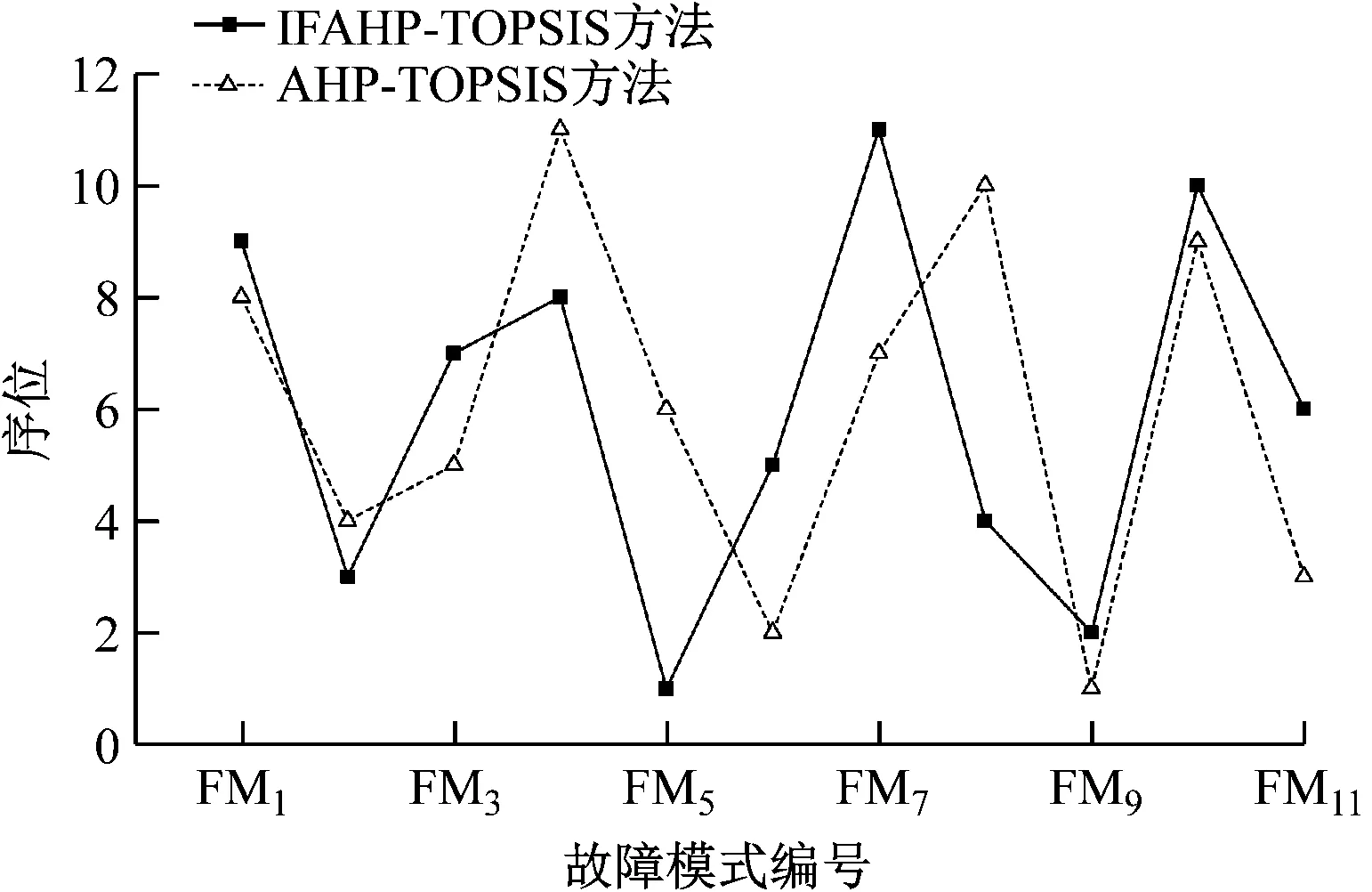
图2 在不同方法下各故障模式的序位对比Fig.2 Sequence comparison of failure modes based ondifferent methods

图3 不同方法下二级风险评估指标权重的对比Fig.3 Comparison of criteria weights at different methods

2种方法风险评估指标的权重分配差异较大，AHP-TOPSIS方法中C1的权重明显高于其他风险评估指标，C3和C6的权重相对较低。这是由于本文采用的是多准则层体系，在计算层次总排序时需要由高准则层指标权重加权确定低准则层指标权重。在进行加权过程中，风险评估指标间权重的差距会成倍增大，可能会出现由某单一风险评估指标确定最终序位的情况，这明显不符合实际。并且，风险评估指标C1偏向为定性指标，含有不确定因素，受主观影响较大，评分专家对C1打分的细微差异会导致故障序位的大幅变化。所提出的IFAHP-TOPSIS方法综合考虑了主观和客观因素，以动态组合方式得到复合权重，分配更为合理；同时引入模糊理论处理不确定因素，所得序位结果也更符合实际。此外，IFAHP-TOPSIS方法无需进行一致性检验。

假设新增故障模式FM12，每个风险评估指标按最高风险进行打分，同样采用AHP-TOPSIS方法和IFAHP-TOPSIS方法进行风险评估，所得故障序位见表16。

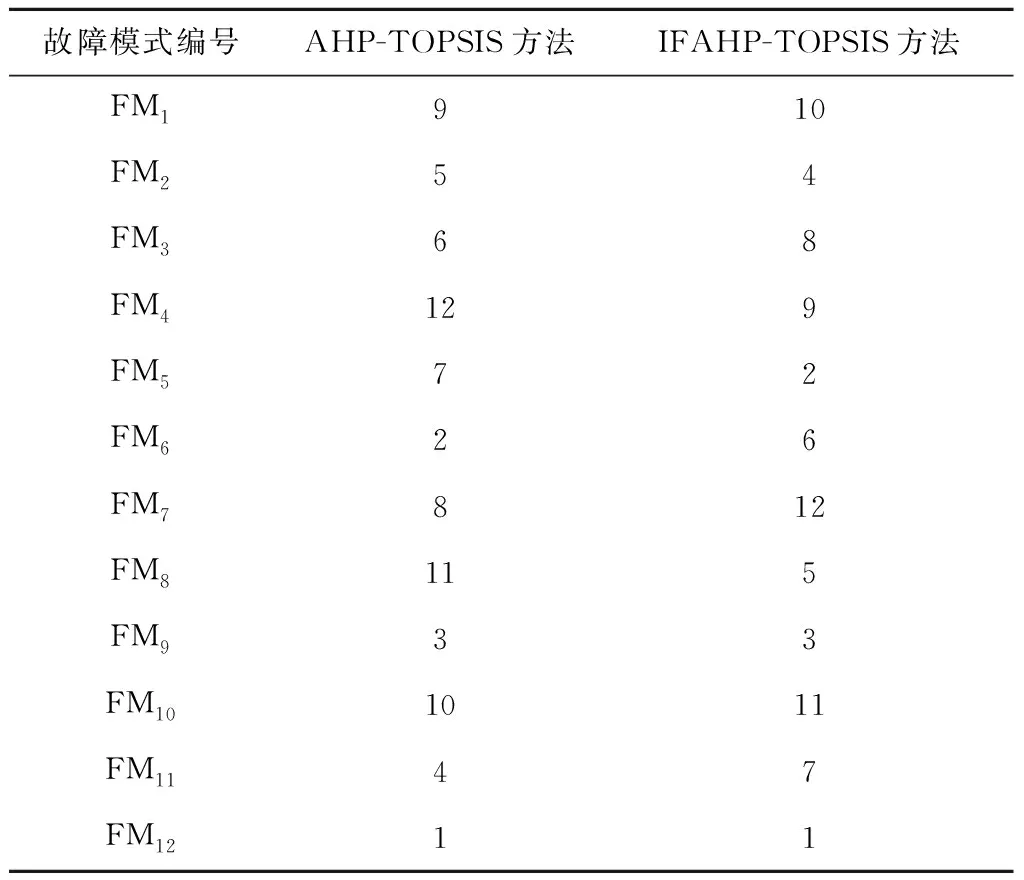
表16 增加新故障模式后的序位对比

与原排序结果对比发现，采用AHP-TOPSIS方法所得序位结果发生了逆序问题。原排序结果中FM6的序位低于FM9，在新排序结果中FM6的序位高于FM9；而IFAHP-TOPSIS方法的新排序结果中除了新增加的故障模式FM12外，其余故障模式序位均无变化。主要原因是采用传统TOPSIS方法计算最终序位时，其风险评估指标权重改变了原决策数据间的关系结构，导致出现逆序问题；而 IFAHP-TOPSIS方法是先将决策矩阵标准化，确定正、负理想解，再使用风险评估指标权重计算各评价方案与正、负理想解之间的距离。所提出的IFAHP-TOPSIS方法既不会改变原始数据结构，又符合权重作为风险评估指标相对重要性的本意，有效解决了逆序问题。

4 结 论

与AHP-TOPSIS方法相比，所提出的IFAHP-TOPSIS方法引入了模糊理论，应用模糊数对主观和模糊信息进行量化描述，能够处理评价过程中的不确定因素；将优先判断矩阵转换为模糊一致性矩阵，无需进行一致性检验，实际应用更加方便；综合考虑主、客观因素，以动态方式将AHP与熵权法相结合，降低了主观敏感度，权重分配更为合理；改进了传统TOPSIS方法中的距离计算公式，解决了增减评价方案会出现逆序的问题，评估结果更符合实际。