一种分析四级离心泵转子系统模态的计算方法
2021-09-24高红斌贡毅超霍小华
高红斌, 贡毅超, 霍小华
(1.山西大学 自动化与软件学院,太原 030013; 2.中国电子科技集团公司第三十三研究所,太原 030032)
振动是旋转机械中非常普遍的一种运动现象,也是导致设备发生故障的主要原因之一[1]。因多级离心泵能头大、易调节、高效工作区宽,常被作为动力设备广泛应用于电厂给水、热力循环水和生活供水等场合。叶轮转子系统作为离心泵最核心的工作部件,工作时直接与液体相互作用,无论是否在工况运行都会产生多种振动[2-3]。这些振动不仅可能会造成故障,还可能导致严重的安全事故[4-5],若在临界转速附近运行将可能产生更大的危害[6]。因此,众多学者对离心泵的模态特征特别是临界转速(固有频率)进行了研究。在目前众多的理论分析中,采用最多的是解析法[7]和三维模拟仿真法[8],解析法简便快捷但是计算所得固有频率的误差比三维模拟仿真计算所得结果的误差大,三维模拟仿真所得结果误差很小但需要内存很大的计算机才能完成[9]。因此,提高解析法的求解精度值得研究。
质量偏心和不平衡造成的转子系统径向振动受到国内外学者的重视[10-11]。离心泵在制造中及工作中的磨损和汽蚀等都会使叶轮产生质量偏心[12-13],而目前有关叶轮质量偏心对模态影响方面的研究较少。笔者以四级离心泵转子系统为例,在常用的简化集中质量解析法的基础上寻求优化计算方法,以提高解析法结果的精度,并以新的计算方法为基础分析叶轮质量偏心对多级离心泵模态的影响,从而为多级离心泵的结构设计、故障诊断及运行调节提供理论依据。
1 数学模型
由牛顿经典力学可知,对于任一系统或者物体,其广义动力学方程可表示为:
(1)
式中:M为质量矩阵;C为黏性阻尼矩阵;A为柔度矩阵;x为位移向量;τ为时间;F为外部激励。
图1为某典型悬臂式四级离心泵转子系统结构图,其安装方式见图2。泵轴通过轴承被支撑在悬臂架上,就像一根悬臂梁,设外伸部分轴的长度为l。4个叶轮被等间距地固定在泵轴悬臂侧一端,叶轮4与右侧悬臂架之间为轴端填料密封装置,设其轴向距离为s,则2个叶轮之间的轴向距离b为:

图1 悬臂式四级离心泵转子系统Fig.1 Rotor system of cantilever four-stage centrifugal pump

图2 悬臂式四级离心泵转子系统安装方式Fig.2 Installation mode of cantilever four-stagecentrifugal pump rotor system
(2)
由梁的弯曲变形理论可知,叶轮1在叶轮1、叶轮2、叶轮3和叶轮4处的柔度影响系数分别为:
(3)
(4)
(5)
(6)
式中:E为泵轴弹性模量;I为泵轴惯性矩。
叶轮2在叶轮1、叶轮2、叶轮3和叶轮4处的柔度影响系数分别为:
(7)
(8)
(9)
(10)
叶轮3在叶轮1、叶轮2、叶轮3和叶轮4处的柔度影响系数分别为:
(11)
(12)
(13)
(14)
叶轮4在叶轮1、叶轮2、叶轮3和叶轮4处的柔度影响系数分别为:
(15)
(16)
(17)
(18)
由于悬臂架对泵轴有较好的轴向定位作用,轴向上泵轴右端通过联轴器与电机实现紧连接,同时忽略扭转振动和陀螺力矩的影响,因此只考虑转子系统的弯曲振动。由图2可以看出,叶轮比轴的径向尺寸大得多、轴向尺寸小得多,因此适合采用集中质量解析法来分析其动力学特性。设叶轮1~叶轮4的质量分别为m1、m2、m3和m4,黏性阻尼系数为c,则由式(1)~式(18)可以得到研究中常用的简化集中质量解析法[14]的悬臂式四级离心泵转子系统在弯曲方向上的拉格朗日动力学方程,其中:
(19)

(20)
(21)
(22)
由式(19)和式(21)可得到集中质量解析法的悬臂式四级离心泵转子系统的特征方程为:
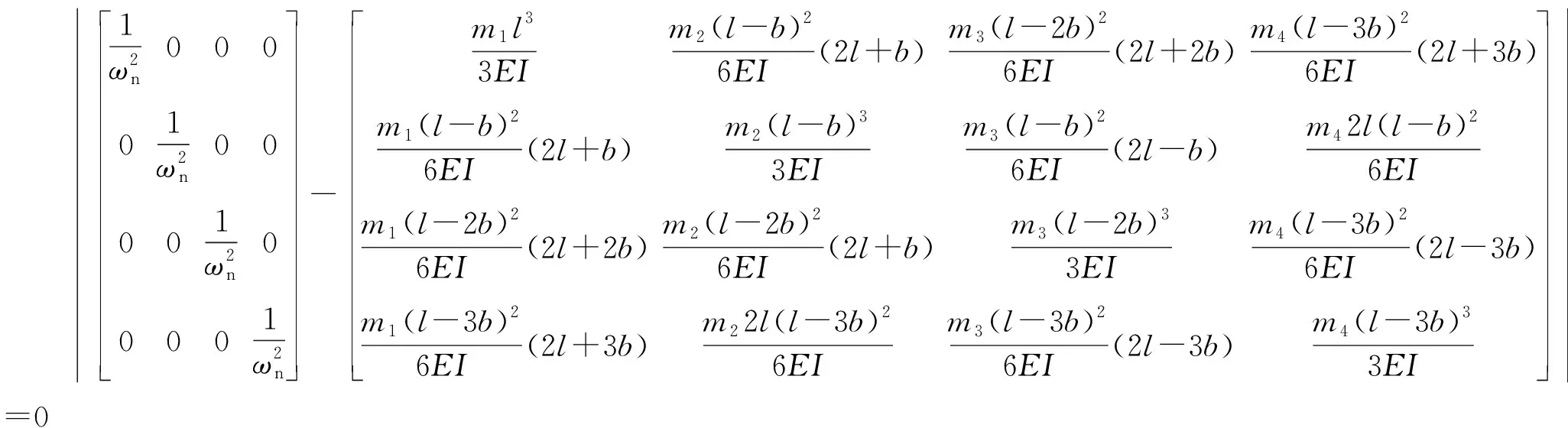
(23)
式中:ωn为四级离心泵转子系统的固有圆角频率。
式(21)所示的柔度矩阵为非对称的正定矩阵,且其秩为4,即为满秩矩阵,因此该矩阵不仅具有4个特征值,而且其特征值均为正的实根。采用式(23)对图1中悬臂式四级离心泵的模态进行计算,其中转子系统的参数见表1。表1中,m为每个叶轮质量;l、s表示的尺寸见图2;d为悬臂外伸部分泵轴直径;ρ、μ分别为系统材料的密度和泊松比。

表1 转子系统参数
由此可以求得该四级离心泵在弯曲方向的固有频率,结果如表2所示。
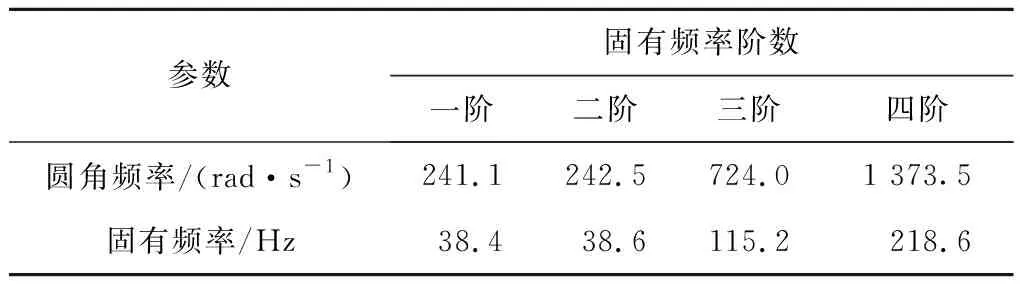
表2 解析法求得的固有频率
该泵的额定转速为1 470 r/min(24.5 Hz),而工程中转速可调的多级离心泵的转速范围一般不超过6 000 r/min(100 Hz)。可见,在同步转速为1 500 r/min的三相电机拖动下,该泵干态运行不会产生共振,而在同步转速为6 000 r/min时该泵干态运行可能会发生2次共振。
将所得第四阶固有频率及该泵的结构和质量等相关参数代入如下特征方程式:
(24)
可以得到该四级离心泵转子系统的振型矩阵为:
r=[r1r2r3r4]=

(25)
式中:r1、r2、r3、r4分别为各阶振型向量解。
各阶振型如图3所示。由图3可知,在前三阶固有频率下叶轮1的变形量最大,4个叶轮的变形方向一致,但其他3个叶轮的相对变形程度有较大差异。在第四阶固有频率下4个叶轮中心的相对径向变形最严重,叶轮1与叶轮2、叶轮3和叶轮4的变形方向相反,且变形量最大的是叶轮3,可见在第四阶固有频率下工作对整个轴系的破坏性最大。
2 三维模拟仿真
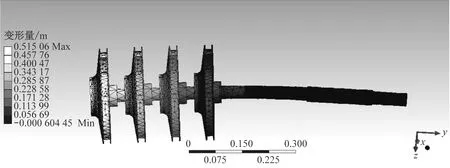
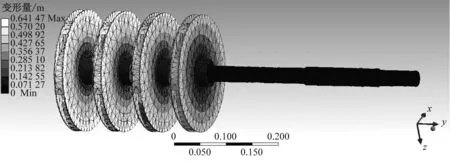
研究[9,15]表明对于附有集中质量块的悬臂梁结构,由ANSYS workbench求得的梁系统的纵向各阶固有频率与实验结果基本吻合。将固定于泵轴的叶轮视为集中质量,泵轴又被固定安装于悬臂架上,因此符合附有集中质量块的悬臂梁的特征,故采用ANSYS workbench对图1中悬臂式四级离心泵转子系统进行模态分析,并作为理想结果与前面建立的数学模型的计算结果进行比较。根据表1中该悬臂式四级离心泵参数设置好材料属性,对其划分网格得到有限元分析模型,再按照图2所示转子系统的安装方式对泵轴中与两轴承接触处施加径向固定约束。利用ANSYS workbench求出该泵的前4阶固有频率分别为38.9 Hz、39.4 Hz、126.1 Hz和247.9 Hz,相应的模态结果如图4所示。

(b) 第二阶振型

(d) 第四阶振型图3 各阶振型图Fig.3 Patterns for each order
由图4(a)~图4(c)可以明显看出,在前三阶固有频率时,整个泵轴中叶轮1处的变形量最大、叶轮2处的变形量次之、叶轮4处的变形量最小。前两阶固有频率比较接近,第一阶固有频率下与第二阶固有频率下转子系统的模态分布特征很相近;每个叶轮在第一阶固有频率下与在第二阶固有频率下的模态分布特征也相似。第三阶固有频率下4个叶轮中心区域的应变差异减小,第四阶固有频率下轴系发生了严重弯曲。这些特征与前面的数学模型求解结果一致。

(a) 第一阶振型
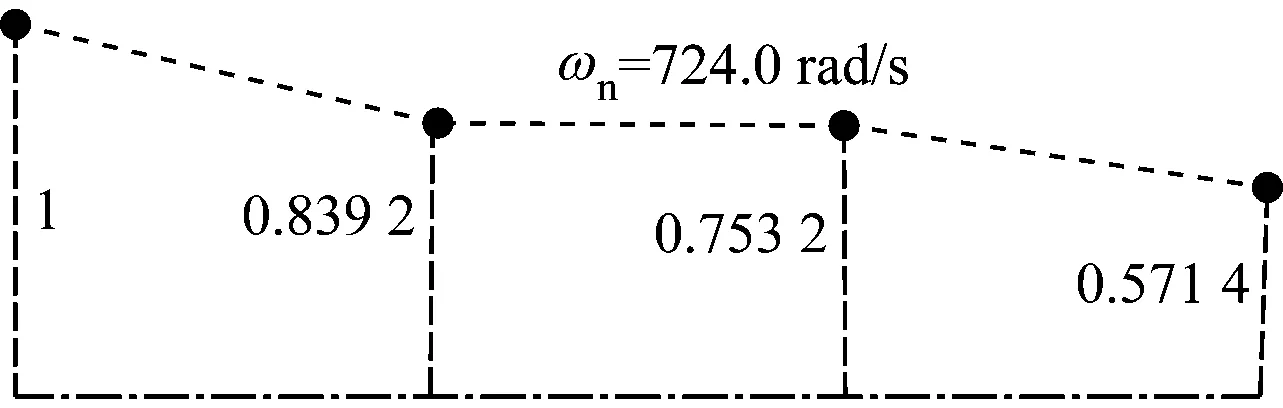
(c) 第三阶振型

(c) 三阶模态
(a) 一阶模态
(c) 三阶模态

(a) 一阶模态
3 优化的数学模型
从前述分析可知,如果数学模型与三维模拟仿真得到的固有频率一致,则2种方法计算得到的振型及模态分布特征也会相同。因此,提高固有频率的计算精度是提高悬臂式四级离心泵转子系统模态分析准确性的基础。将数学模型与三维模拟仿真所得前四阶固有频率进行比较,结果见表3,其中误差1表示三维模拟仿真结果与前述解析法所得数值计算结果的误差。

(b) 二阶模态

(d) 四阶模态图4 四级离心泵转子系统ANSYS分析结果Fig.4 Analysis results of four-stage centrifugal pumprotor system by ANSYS

表3 数值计算结果与三维模拟仿真结果Tab.3 Numerical calculation results and 3D simulation results
由表3可以看出,由前面所建立的悬臂式四级离心泵转子系统模态方程所求得的一阶和二阶固有频率误差较小,但是随着阶数的增大,误差越来越大,四阶固有频率的误差达到11.82%(相当于相差1 758 r/min)。同时,由数学解析得到的各阶固有频率均小于三维模拟仿真结果,说明集中质量解析法所得的结果小于连续体法计算所得结果。以上分析方法使用的材料参数相同、建模使用的尺寸数据也相同,然而其结果却出现了差异,数学计算结果是根据式(23)计算得出的,主要原因如下:(1) 式(23)将原本连续的泵轴转子系统人为分割为4个质量集中部分;(2) 矩阵中质量仅考虑了叶轮质量,没有考虑轴系的质量;(3) 矩阵中抗弯刚度仅考虑了轴系截面的惯性矩而没有考虑叶轮惯性矩的影响。研究表明[16],质量被集中的个数越多,所得固有频率与实际越接近,因此笔者研究泵轴质量和叶轮抗弯刚度对悬臂式四级离心泵转子系统固有频率的影响,并以此为基础分析叶轮质量偏心对该转子系统固有频率的影响。
由于悬臂梁被固定部分的变形量远小于外伸部分,因此为了提高计算精确性,在质量矩阵中仅计入泵轴在悬臂架外(左侧)的质量。如图2所示,将2个叶轮之间的轴质量平均折算至每个叶轮,即4个叶轮处轴段的质量等效为:
(26)
(27)
(28)
(29)
叶轮通过键与轴过盈相连,这相当于泵轴中串联了4个叶轮,叶轮的存在必然影响整个泵轴的变形。因此,转子系统的抗弯刚度EI应该由泵轴的抗弯刚度EsIs和叶轮的抗弯刚度EiIi组成:
EI=EsIs+EiIi
(30)
由材料力学知识可知,在推导弯曲应力和弯曲变形时,将与梁的长度尺寸有关的参数放置于分子中,而将与截面和材料有关的参数放置于分母中,且在集中力下等截面梁的弯曲应力和弯曲变形与梁的长度成正比。模态分析涉及弯曲应力和弯曲变形,属于广义材料力学的研究范畴,因此在式(30)中必须考虑叶轮轴向尺寸。在叶轮的任一轴面中,叶片的截面积远小于前后盖板的截面积,因此仅考虑盖板造成的抗弯刚度对转子系统模态的影响。设盖板的厚度为t、叶轮外径为D、集中质量段轴向尺寸为T,则根据串联轴刚度的计算方法,式(30)可以表示为:
(31)
即,
(32)
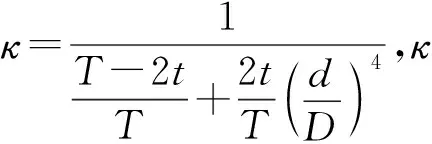
将式(27)~式(29)和式(32)代入式(23)可以得到悬臂式四级离心泵转子系统优化后的数学模型特征方程为:
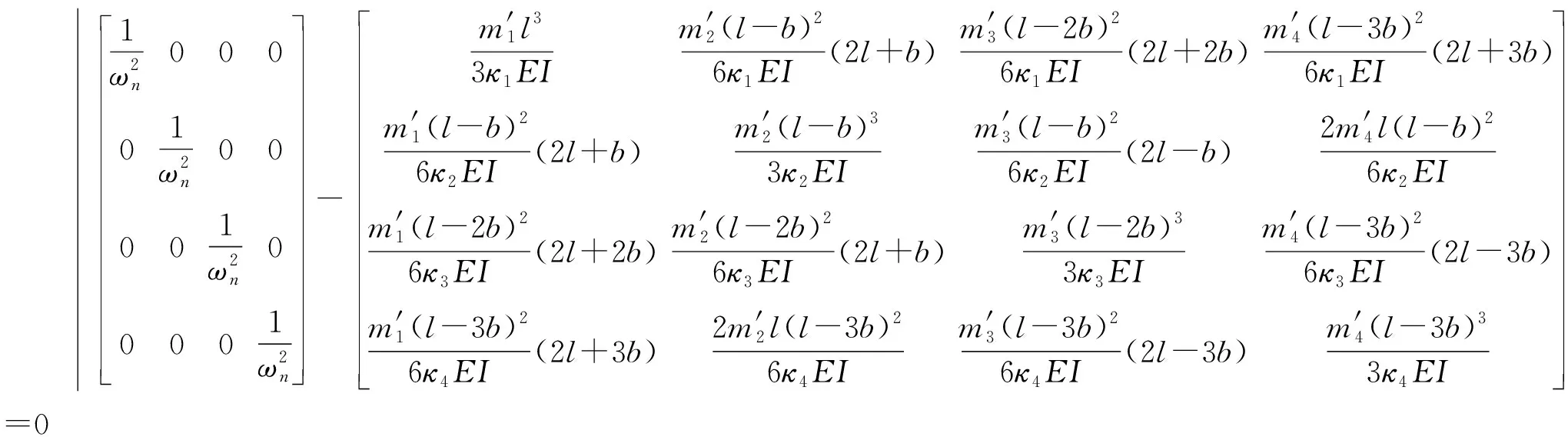
(33)
其中:
将前述相关参数代入式(33)得到各集中质量处模态刚度修正系数κ1=1.052 6、κ2=1.025 6、κ3=1.025 6、κ4=1.008 1和优化后的固有频率解析计算结果,如表3所示,其中误差2表示三维模拟仿真与式(33)求解所得固有频率的误差。由四处的模态刚度修正系数值可以看出,叶轮1对转子系统刚度的影响最大、叶轮4对转子系统刚度的影响最小。由表3可以看出,优化后同样随着阶数的增大,解析计算的误差也增大,但每阶固有频率的误差已经由优化前的1.28%、2.03%、8.64%和11.82%分别下降至0.77%、1.02%、3.41%和4.52%,特别是高阶固有频率的精确性有了非常显著的提高。综上,系统质量减小必然惯性减小,使得反应速度变快即固有频率增大,系统刚度减小必然弹性势能减小,使得反应速度变慢即固有频率减小,由式(23)求得的各阶固有频率均小于三维模拟仿真结果,说明对转子系统叶轮刚度的简化是造成计算结果误差的主要因素,而由本文提出的优化方法可以大大提高解析法的准确性。
4 叶轮质量偏心对模态的影响
采用前述优化的数学模型分析叶轮质量偏心对转子系统模态的影响,并与三维模拟仿真结果进行比较。在图4中若某叶轮后盖板z轴上距离轴心e处出现一半径为r的圆形质量缺损,造成了叶轮质量的偏心,则偏心的质量Δms=ρπr2t,缺失质量在该方向的惯性矩ΔIm为:
(34)
将式(34)代入式(32),得到此时模态刚度修正系数κ的表达式为:
(35)
如同式(33),将式(35)、式(32)、缺失质量的叶轮质量代入式(23)可以得到叶轮质量偏心时悬臂式四级离心泵转子系统优化的特征方程,从而得到各阶固有频率及相应的振型。下面分析该四级离心泵的每个叶轮后盖板e=60 mm处出现r=30 mm的质量偏心时对四级离心泵模态产生的影响。
首先采用三维模拟仿真软件对叶轮1发生质量偏心时该转子系统的模态进行分析,得到其前四阶固有频率分别为39.8 Hz、40.3 Hz、129.9 Hz和252.7 Hz,相应的模态结果如图5所示。
采用上述叶轮质量偏心时的优化数学模型计算出叶轮1发生质量偏心时该转子系统的前四阶固有频率分别为39.4 Hz、39.7 Hz、124.8 Hz和240.4 Hz,将其与三维模拟仿真结果进行比较,如表4所示。

(b) 二阶模态
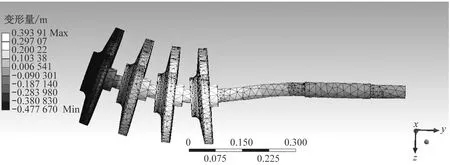
(d) 四阶模态图5 叶轮1质量偏心时ANSYS分析结果Fig.5 Analysis results of mass eccentricity of impeller 1 by ANSYS
由表4可知,由优化后的数学模型求得的叶轮1质量偏心时转子系统的固有频率与三维模拟仿真得到的固有频率的误差随着阶数的增大而增大,但四阶固有频率的误差也小于5%。同时,表4中叶轮1质量偏心时2种结果的4个误差1.01%、1.45%、3.93%、4.87%均大于表3中无质量偏心时2种结果的4个误差0.77%、1.02%、3.41%和4.52%,可见利用本文优化的数学模型求解叶轮1质量偏心时悬臂式四级离心泵转子系统所得模态结果比求解无质量偏心时误差略大、精确性略低。
同上,采用三维模拟仿真分别对叶轮2、叶轮3和叶轮4发生质量偏心时该四级离心泵转子系统的模态进行分析,采用上述叶轮质量偏心时的优化数学模型再分别计算出叶轮2、叶轮3和叶轮4发生质量偏心时该转子系统的前四阶固有频率,将三维模拟仿真和数值计算结果得到的各阶固有频率进行比较,如表4所示。由于本节主要分析叶轮质量偏心对固有频率变化的影响,这三级叶轮质量偏心时的三维仿真云图未给出。
由表4可知,当叶轮1产生质量偏心时各阶固有频率的值最大,叶轮2产生质量偏心时各阶固有频率的值次之,叶轮4产生质量偏心时各阶固有频率的值最小,即随着产生质量偏心的叶轮位置远离悬臂处(即越靠近叶轮1),整个转子系统的固有频率越大;由本文优化的数学模型求得的各级叶轮质量偏心时转子系统的固有频率与三维模拟仿真结果的误差随着阶数的增大而增大,但最高阶固有频率的误差亦小于5%,完全可以满足工程需要,因此本文优化的数学模型具有较高的精度。同时,由表4和表3可知,由本文优化的数学模型求解叶轮质量偏心时比求解叶轮无质量偏心时悬臂式四级离心泵转子系统固有频率的误差大,叶轮发生质量偏心时各阶固有频率的值均略有增大。

表4 叶轮质量偏心时优化数学模型与三维模拟仿真得到的固有频率
5 结 论
(1) 分析了悬臂式四级离心泵转子系统的质量负载、阻尼特性和柔度影响系数的计算方法,建立了简化的集中质量动力学数学模型和融合轴系质量及模态刚度修正系数的优化数学模型,得到2种模型下转子系统固有频率的求解方法。
(2) 集中质量解析法得到的离心泵转子系统的固有频率略小于三维模拟仿真结果。
(3) 由本文优化后的数学模型求得的四阶固有频率的误差由优化前的1.28%、2.03%、8.64%和11.82%分别下降至0.77%、1.02%、3.41%和4.52%,对转子系统中叶轮刚度的简化是造成计算结果误差的主要因素。
(4) 叶轮发生质量偏心时各阶固有频率的值均略有增大,产生质量偏心的叶轮位置越靠近吸入室侧,对转子系统固有频率的影响越大。
(5) 由本文优化的数学模型求解叶轮质量偏心时比求解叶轮无质量偏心时悬臂式四级离心泵转子系统固有频率的误差大,但最大误差在5%内,完全可以满足工程需要。
