基于改进型模糊线性自抗扰控制器的SCR脱硝系统优化控制

2021-09-24牛玉广潘翔峰曹国庆庄志宝

动力工程学报 2021年9期

杜鸣，牛玉广，潘翔峰，曹国庆，马强，庄志宝

(1.华北电力大学新能源电力系统国家重点实验室，北京 102206；2.吉林电力股份有限公司白城发电公司，吉林白城 137000)

选择性催化还原(SCR)技术是我国火力发电厂最常用的烟气脱硝技术之一[1]。由于SCR脱硝系统具有大迟延、大惯性、多干扰、时变性和非线性等特点，采用比例-积分-微分(PID)控制器难以获得理想的控制效果，因此需要针对SCR脱硝系统设计更加精确的控制系统[2]。

国内外学者针对SCR脱硝系统提出了很多优化控制策略，其中预测控制技术是一种重要的优化控制方式。刘吉臻等[3-4]利用多变量预测控制技术进行优化控制研究。俞基安等[5]基于阶梯式广义预测控制算法构建了SCR脱硝系统的优化控制策略。侯鹏飞等[6]提出了一种适用于变工况的多模切换动态矩阵控制(DMC)与PID相结合的串级预测控制方法(DMC-PID方法)。王瑾等[7]利用粒子群算法根据出口NOx质量浓度设定值对喷氨阀门开度设定值进行了优化，进而完成了SCR脱硝系统的优化控制。周洪煜等[8]提出了基于混结构-径向基函数(RBF)神经网络(MS-RBFNN)的喷氨量最优控制方法。牛玉广等[9-10]利用单神经元自适应-人工鱼群滚动寻优控制算法(RSNAAFS)对喷氨量进行了优化控制，并提出了一种SCR脱硝系统分区控制方案。针对SCR脱硝系统的控制问题，上述研究中所提算法均较为复杂，对模型精确性要求较高，且现场扰动源较多，因此难以直接应用在电厂组态中。

自抗扰控制(ADRC)技术将系统未建模动态和未知干扰作为总扰动，通过扩张状态观测器进行估计并在反馈控制中进行消除[11]。ADRC不依赖系统模型，鲁棒性强，适用于复杂的现场控制环境。Gao[12]对非线性ADRC进行了线性化，得到了线性自抗扰控制器(LADRC)，并提出带宽概念整定控制器参数。黄宇等[13]将LADRC应用到SCR脱硝系统的外回路控制中，并给出了控制器参数整定方法。姜家国等[14]利用Smith预估器对ADRC进行了改进。李健等[15]对基于迟延部分补偿的改进型LADRC在SCR脱硝系统中的应用进行了理论研究。Wu等[16-17]提出了一种利用高阶惯性环节代替纯迟延补偿的改进型LADRC，并将该控制器应用到循环流化床锅炉的控制中，证明了该类控制器具有相比于LADRC、比例积分(PI)等控制器的优越性。

笔者在现有研究的基础上，首次提出一种改进型模糊线性自抗扰控制器(Fuzzy-MLADRC)，并将其应用至SCR脱硝系统的优化控制中。

1 SCR脱硝系统

SCR脱硝系统的一般工作原理如下：利用催化剂使加入的还原剂与烟气中的NOx反应，将NOx还原成N2和H2O，还原剂一般采用氨气。SCR脱硝控制系统中涉及的主要化学反应为：

(1)

通常催化剂的工作温度在320 ℃以上，但随着灵活性改造的进行，在机组降负荷过程中烟气温度降低，当催化剂低于正常工作温度时面临失效的困境。因此，有必要通过相应的改造或使用低温催化剂来提升SCR脱硝系统在低负荷下的安全性。在上述反应过程中，如果喷氨量较小，则还原剂无法与NOx充分反应；如果喷氨量过大，则还原剂会与烟气中的SO2反应，产生的硫酸盐会降低催化剂的脱硝效率和使用寿命，同时会增加运行成本，还会堵塞空气预热器，进而降低锅炉效率。因此，SCR脱硝系统在运行过程中有2个重要的控制目标：控制SCR脱硝系统出口NOx质量浓度达到排放要求；控制氨逃逸率，避免过量喷氨。

典型的SCR脱硝系统串级控制系统结构见图1，其中ρr为出口NOx质量浓度设定值，ρy为出口NOx质量浓度的测量值，d为内外扰动量，GNH3(s)为喷氨量的传递函数，GSCR(s)为烟气脱硝系统出口NOx质量浓度的传递函数，GSCR(s)=K2e-τ2s(1+T2s)-2，s为拉普拉斯算子，K2、T2和τ2分别为该传递函数的比例常数、时间常数和迟延时间。内回路的控制器通常采用PID控制器Gc2(s)，而外回路控制器Gc1(s)是本文的研究重点。

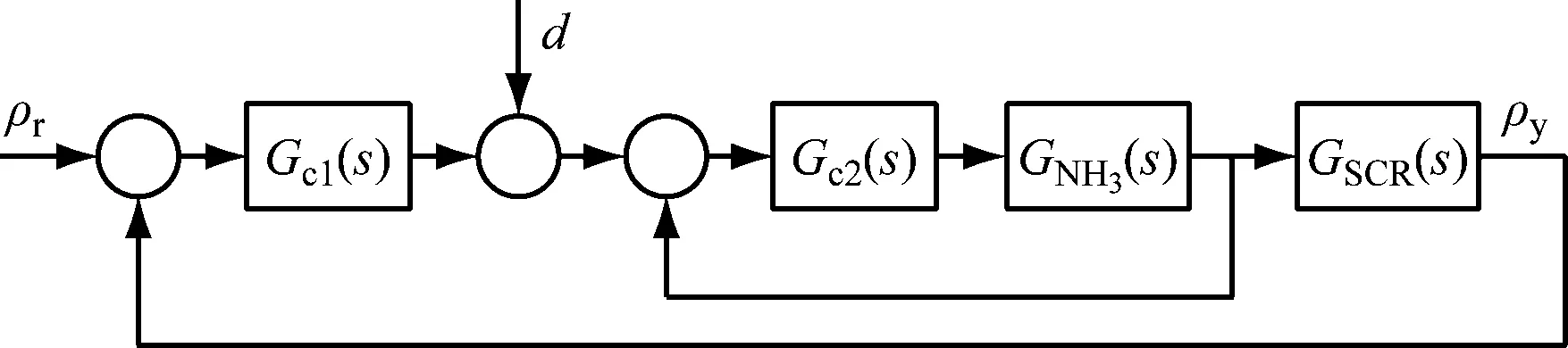
图1 SCR脱硝系统串级控制系统结构Fig.1 Cascade control structure of SCR denitrification system

2 Fuzzy-MLADRC

2.1 2种改进型自抗扰控制器

被控对象通常可以表示为：

(2)

式中：x(t)为状态变量；x(n)(t)为状态变量的n阶导数；u(t)为输入变量；w(t)为扰动变量；y(t)为输出变量；b0为系统增益；g()为系统广义扰动。

将g()扩展为一个新的状态变量，并同时令x1(t)=y(t),x2(t)=y(1)(t),…,xn(t)=y(n-1)(t),xn+1(t)=g(t)。

则系统可进一步表示为：

(3)

其中，

因此，设计的线性扩张状态观测器(LESO)为：

(4)

式中：z(t)为观测器输出估计值矩阵；L0为观测器增益矩阵；uf=u(t)/(Ts+1)n，其中T为补偿环节的惯性时间常数，n为补偿环节的阶次。

基于LESO对系统状态和扰动的估计，系统控制率(即对象的输入变量)可设计为：

(5)

式中：zn+1(t)为广义误差的估计值。

线性状态误差反馈控制率(LSEF)u0(t)为：

u0(t)=k1[r(t)-z1(t)]+k2[r(1)(t)-

z2(t)]+…+kn[r(n-1)(t)-zn(t)]

(6)

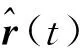
进一步推导可得：

u(t)={k1[r(t)-z1(t)]+k2[r(1)(t)-z2(t)]+…+

kn[r(n-1)(t)-zn(t)]-zn+1(t)}/b0=

(7)

式中：Ko为状态反馈增益矩阵。

针对大迟延对象，Zhao等[18]提出了一种改进型自抗扰控制器DLADRC，改进位置见图2。首先，对被控对象的迟延时间进行估计，然后将改进环节Gc(s)设置成对迟延时间的补偿。

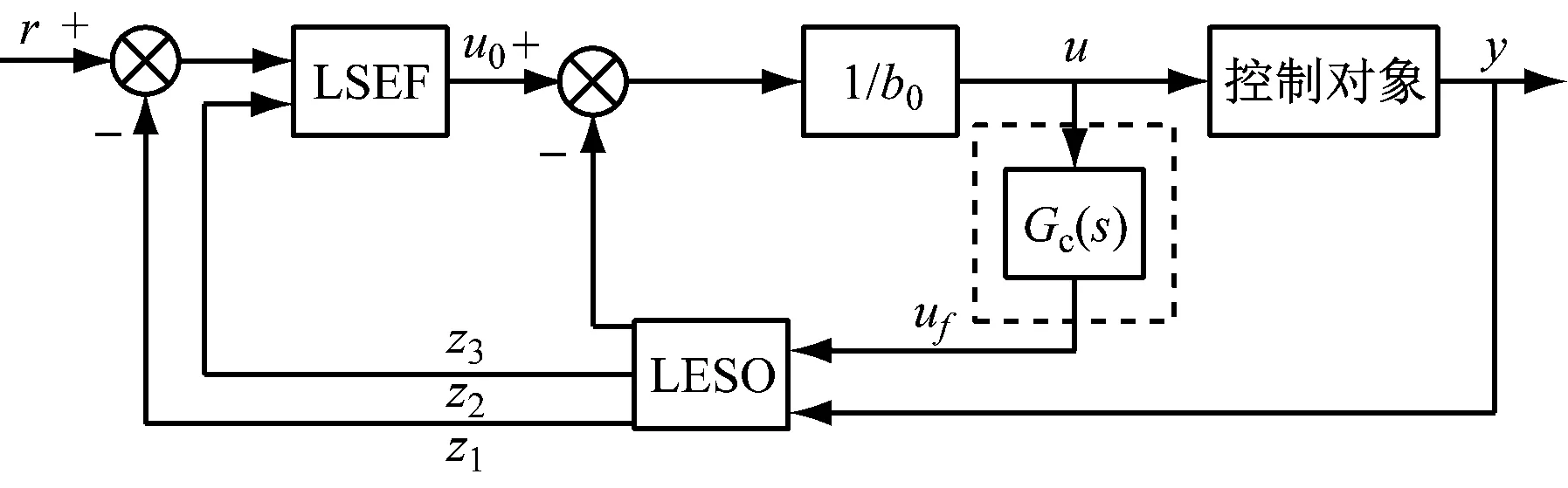
图2 改进型自抗扰控制器的结构示意图Fig.2 Structure diagram of improved ADRC

Gc(s)=e-τs

(8)

式中：τ为迟延时间的估计值。

Wu等[16-17]针对高阶惯性环节提出了另一种改进型的自抗扰控制器MLADRC，该改进之处在于将Gc(s)设置成惯性环节，在扩张状态观测器(ESO)中提前对被控对象的大惯性进行补偿。

(9)

结合带宽概念[17]，以上控制器需要整定的参数包括b0、控制器带宽ωc、观测器带宽ωo、补偿环节的惯性时间常数T和补偿环节的阶次n。

以上2种控制器均是利用被控对象的部分信息，在扩张状态观测器中对被控对象的迟延时间进行补偿，其中DLADRC需要对被控对象的迟延时间进行较精准的估计，而MLADRC对模型的精确度要求相对较低，因此笔者基于MLADRC并引入参数模糊法则，提出Fuzzy-MLADRC。

2.2 Fuzzy-MLADRC

如图3所示，首先引入参数模糊化环节，选取b0、ωc和ωo3个参数的修正量Δb0、Δωc和Δωo作为模糊控制器的输出，基于Fuzzy-MLADRC的SCR脱硝系统示意图见图4，其中Δy=r(t)-y(t)。

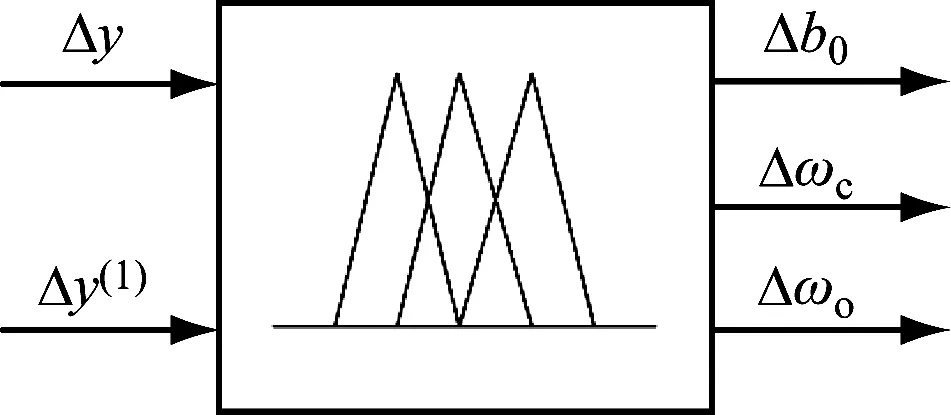
图3 参数模糊化过程Fig.3 Fuzzification process of parameters

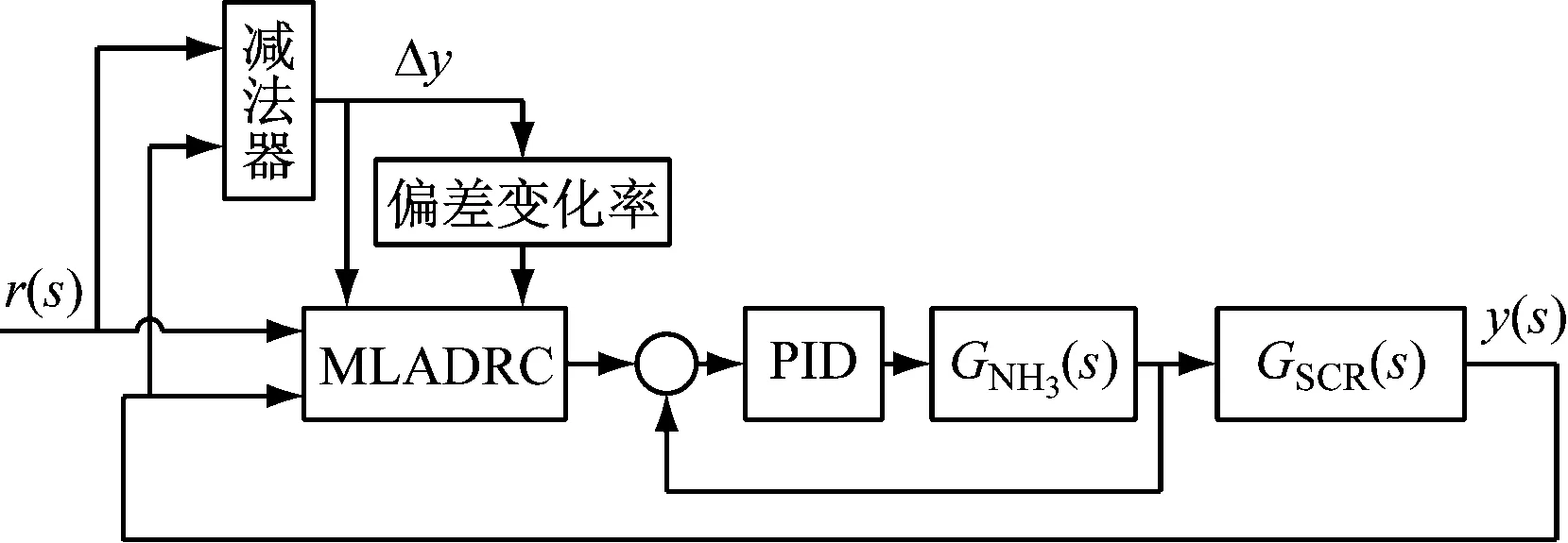
图4 基于Fuzzy-MLADRC的SCR脱硝系统Fig.4 SCR denitrification control system based on Fuzzy-MLADRC

通过式(10)对Fuzzy-MLADRC的参数进行补充。

(10)

式中：b00、ωc0和ωo0均为控制器初始参数。

Fuzzy-MLADRC的输入和输出均采用7个语言变量，相应的语言变量模糊集包括NB、NM、NS、ZO、PS、PM和PB，分别代表负大、负中、负小、零、正小、正中和正大，各语言变量均采用具有较高灵敏度的三角形隶属函数。

b0和ωc决定控制器的控制能力，ωc越大或b0越小，系统响应越快，但会出现超调现象，且振荡加剧。ωo越大，扩张状态观测器对状态误差的控制能力越强，系统的响应能力越强，但对噪声的观测能力也增强，系统输出发生振荡。根据各参数的调节规律，制定各参数模糊整定规则表，见表1～表3。其中，E为输入变量偏差，Ec为偏差变化率。

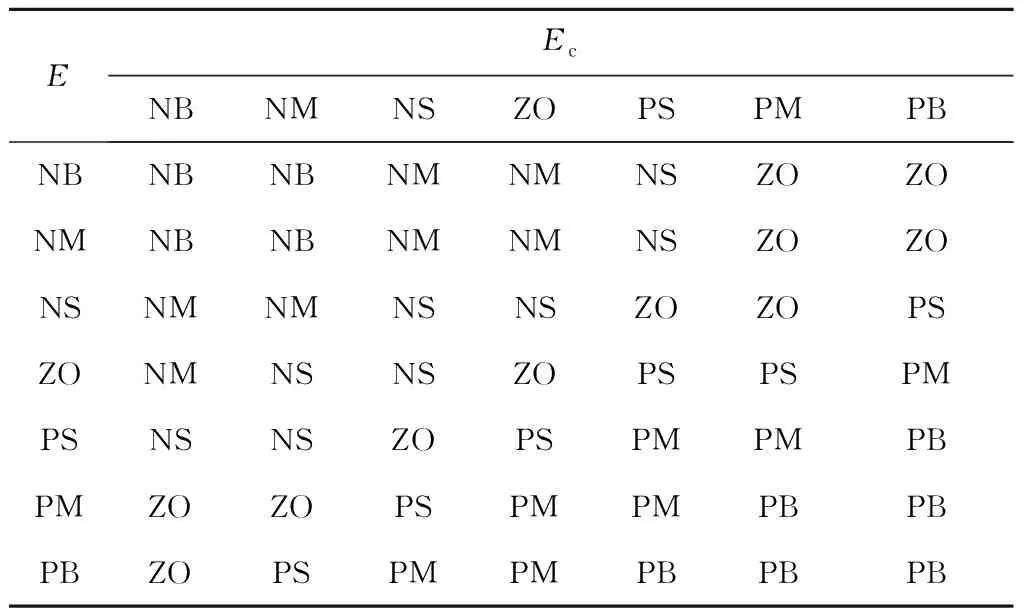
表1 b0的模糊整定规则

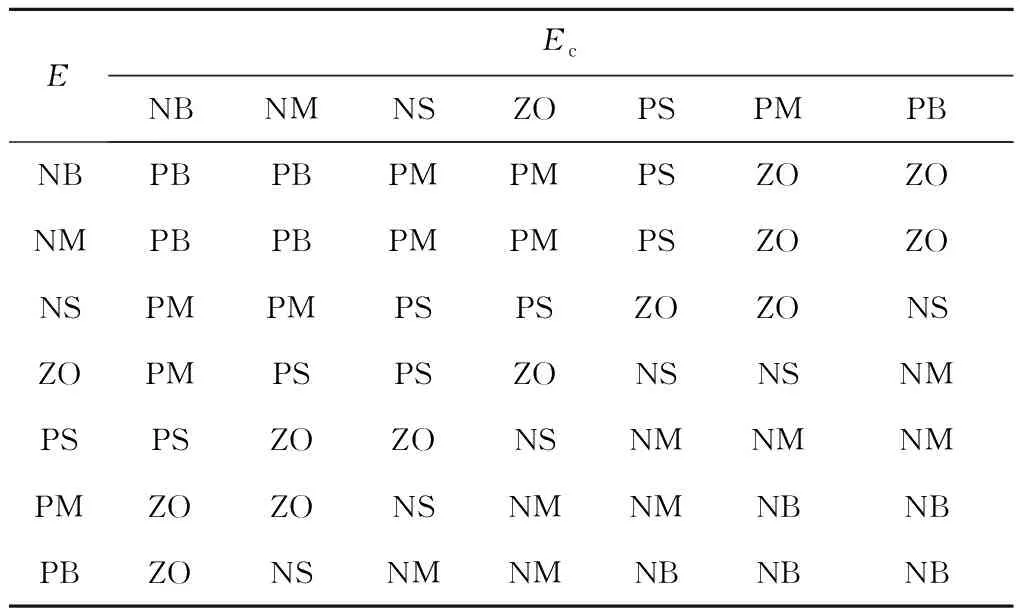
表2 ωc的模糊整定规则

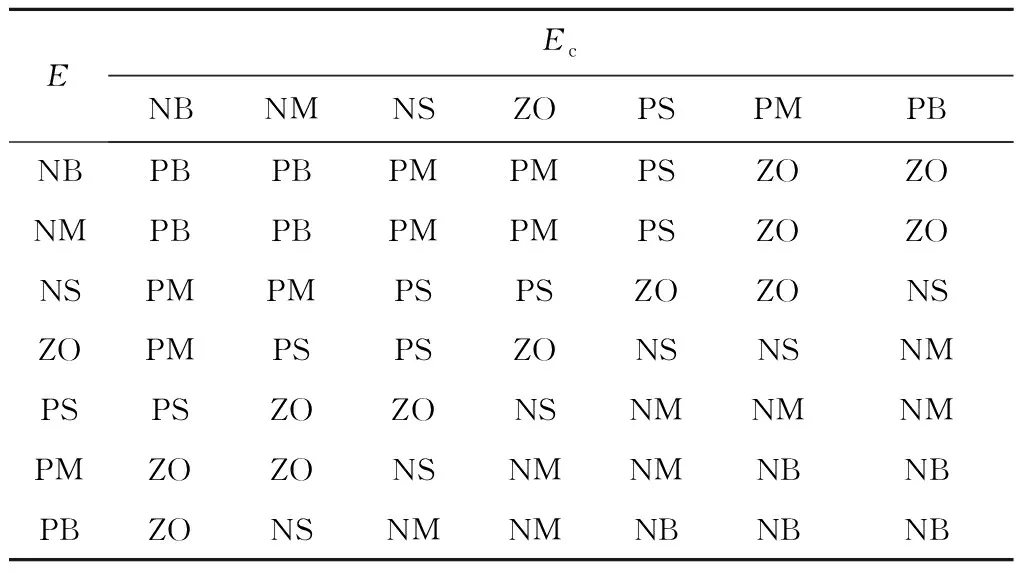
表3 ωo的模糊整定规则

2.3 控制器参数求解方法

由于SCR脱硝系统对象是一个大迟延、大惯性、时变的环节，难以直接确定T和n，因此将其视作待定系数，但从SCR脱硝系统模型中可以对T和n的取值范围进行界定。

采用带有交叉因子的粒子群算法对控制器参数进行寻优，优化目标函数f为：

(11)

3 仿真验证

在80%的机组负荷率下某电厂SCR脱硝系统的控制模型参数见表4。内环采用比例控制方式，比例系数取0.15，外回路分别采用PID、Fuzzy-PI、LADRC、DLADRC、MLADRC和Fuzzy-MLADRC进行仿真研究，自抗扰控制选用二阶LADRC，前4种控制器参数见表5,而Fuzzy-MLADRC的控制器参数在文中已给出，不再赘述。其中，KP为比例系数，Ki为积分系数，Kd为微分系数。

表4 控制模型参数

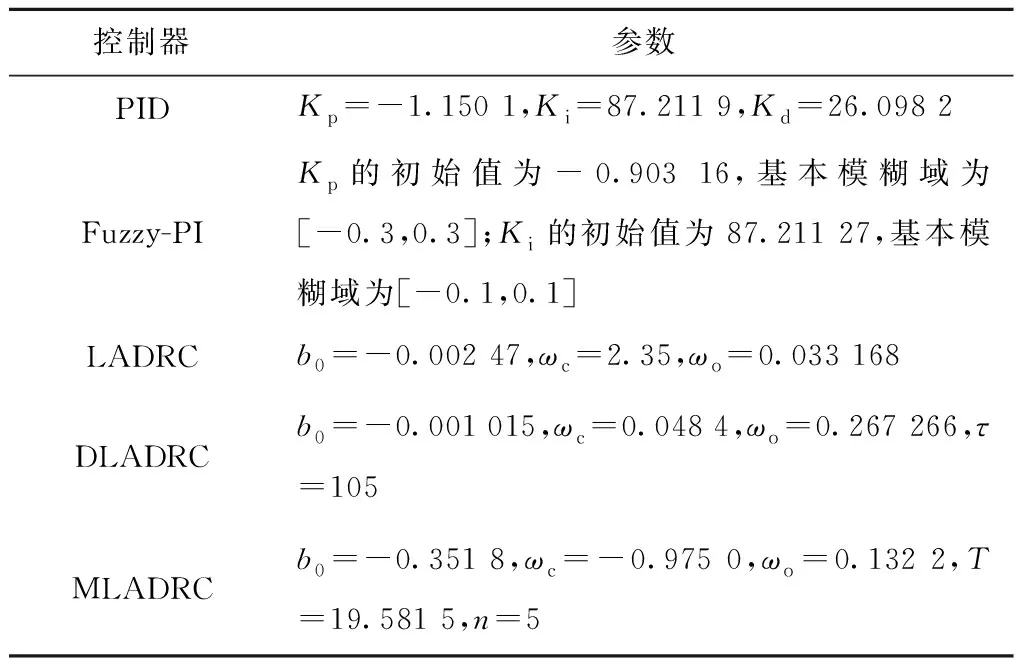
表5 控制器参数

PID控制器结构采用如下形式：Kp×[1+1/(Kis)+sKd]。初始参数b00、ωc0和ωo0采用MLADRC控制参数，选定E的基本模糊论域为[-2,2]，Ec的基本模糊论域为[-3,3]，Δb0的基本模糊论域为[-0.1,0.3]，Δωc的基本模糊论域为[-0.1,0.2]，Δωo的基本模糊论域为[-0.1,0.2]。经粒子群算法寻优，得到Δb0的比例因子为-0.094 2，Δωc的比例因子为1.482 0，Δωo的比例因子为-0.111 1。

3.1 控制效果评估

各控制器的设定值追踪效果和抗扰动能力仿真结果见图5和图6。各控制器的性能评估结果见表6。当采用PID和Fuzzy-PI控制器时，最优指标f分别为165.71和196.62，而LADRC的最优指标为158.29，其他控制器的最优指标更低，因此相较于PID控制器，自抗扰控制器普遍能取得更优的设定值追踪效果。采用Fuzzy-MLADRC控制器时，控制系统的输出能快速跟踪输入指令，并快速稳定到设定值，其上升时间最短(43.28 s)，设定值追踪效果最优。从图6可以看出，DLADRC的抗扰动能力最强，受到扰动后能快速回到设定值附近，其次分别是MLADRC和Fuzzy-MLADRC。

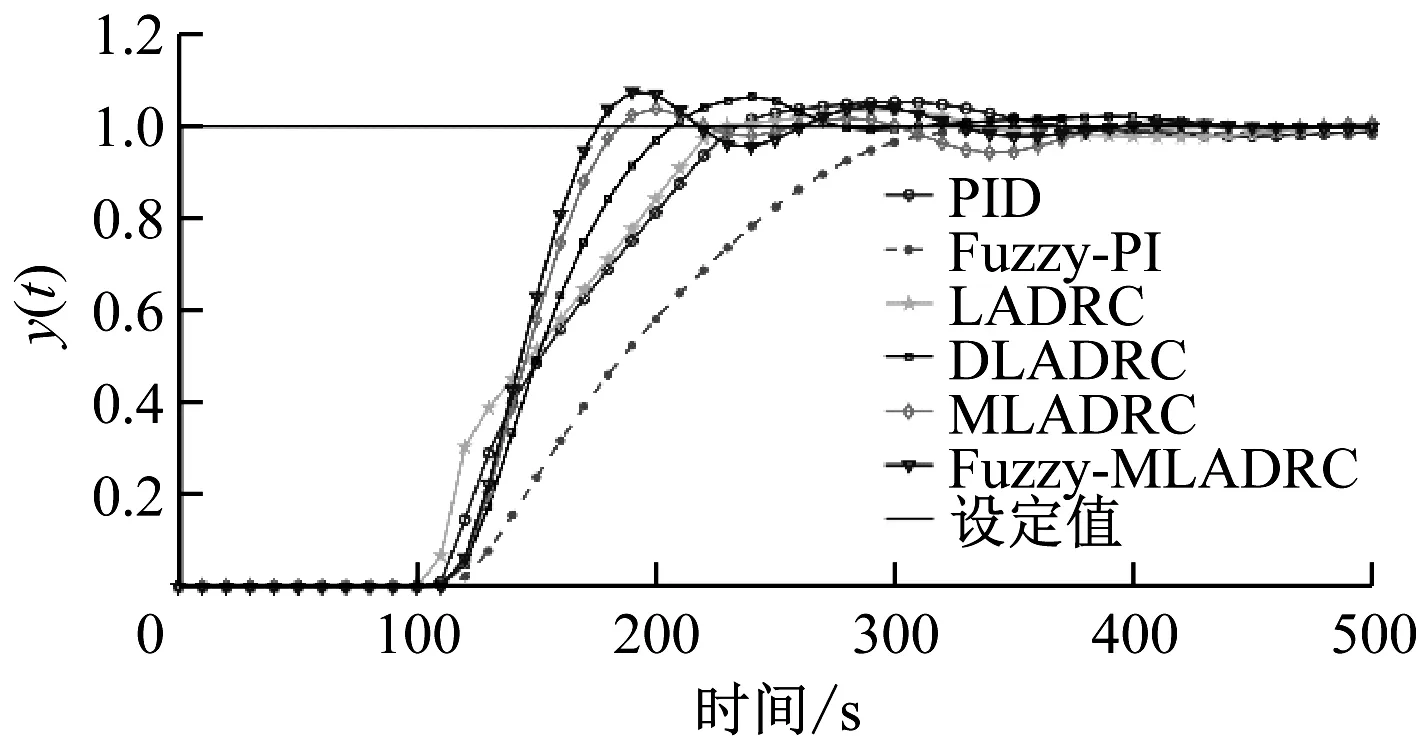
图5 设定值追踪效果Fig.5 Simulation results of set point tracking effect

图6 抗扰动能力仿真结果Fig.6 Simulation results of anti-disturbance ability

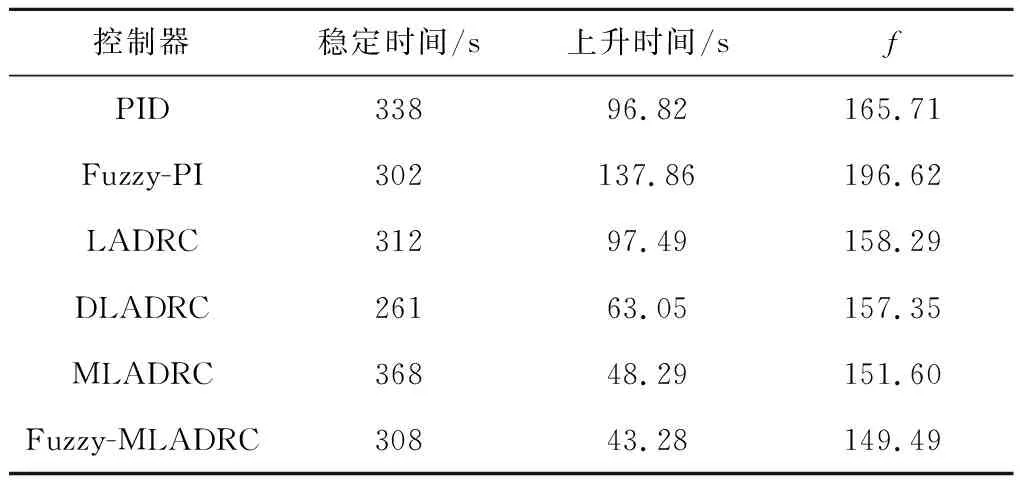
表6 控制器性能评估结果Tab.6 Performance evaluation results of controllers

3.2 控制器的鲁棒性分析

在不同负荷下SCR脱硝系统模型的差异较大，且干扰源复杂，在不同条件下时间常数和迟延时间等变化较大。因此，为检验不同控制器的鲁棒性能，假设扰动引起的SCR脱硝系统模型变化部分全部叠加到外环上。假设模型参数有以下变化：K2=-3.2×(0.8+0.4×ξ1)，T2=25×(0.8+0.4×ξ2)，τ2=105×(0.8+0.4×ξ3)，其中ξ1、ξ2和ξ3∈N(0,1)。在此基础上进行50次蒙特卡洛模拟，结果见图7和表7。

图7 鲁棒性测试结果Fig.7 Results of robustness tests

表7 控制器鲁棒性评估结果Tab.7 Evaluation results of robustness for controllers

从图7和表7可以看出，LADRC和PID均具有相对稳定的控制效果，在每次模拟中最优指标f均保持在相似位置，而DLADRC与MLADRC在模型失配的情况下均出现不同程度控制效果下降的情况，原因在于这2种控制器均对模型精确度有一定要求，特别是对象迟延时间的精确度。当迟延时间失配程度较高时，采用DLADRC时系统会出现发散的情况。随着模型失配的加剧，MLADRC也会出现控制效果变差的情况，但最优指标增幅较小，因此该控制器的鲁棒性比DLADRC更强。与其他控制器相比，Fuzzy-MLADRC的最优指标增幅最小，表明在模型参数失配的情况下该控制器的鲁棒性最好。