杈式折流栅对管壳式换热器壳程性能的影响
2021-09-24刘佳奇王永庆刘遵超
王 珂,刘佳奇,安 博,王永庆,刘遵超
(1.郑州大学 力学与安全工程学院,郑州 450002;2.郑州大学 河南省过程传热与节能重点实验室,郑州 450002)
0 引言
换热器作为能源动力转换的核心设备,广泛存在于核电、化工、制冷等多个行业和国民生活中[1-2]。管壳式换热器是业内最常见的换热设备之一,具有结构简单、适应性强等诸多优点[3-5]。其壳程装配的弓形折流板、格栅支撑板等管束支撑结构[6],一方面可以支撑管束,防止换热管发生振动损坏;另一方面可以引导壳程工质产生不同的流动形式[7],增加流体的扰动程度,提高换热性能。
为了提升管壳式换热器的壳程换热效率,许多研究者对管束支撑结构不断进行创新设计和优化[8]。某公司研发的折流杆换热器具有流阻小、易于清洁,且高雷诺数下传热效率高等诸多优势[9]。可是,在较低流量工况下,壳程介质不易达到充分的湍流状态,传热能力较弱[10]。WANG[11]使用激光多普勒测速仪对螺旋折流板换热器的速度场进行了试验研究,结果表明,螺旋折流板的最佳螺旋角取决于换热器壳程工质的雷诺数。范继珩等[12]针对弓形折流板换热器流动阻力大的问题,对弓形板进行开孔处理,通过数值研究发现,壳程流动死区明显减少,传热性能降低,但综合性能同比增强。MELLAL等[13]数值研究了弓形折流板排布对换热器传热的影响,得出折流板方位角为180°、折流板间距为64 mm是保证混合流动的最佳设计。古新等[14]通过设计正交试验,综合研究了扭转流换热器关键参数的影响,得出相邻两组折流板的间距是影响扭转流换热器壳程综合性能的主要因素。
本文在已有的研究基础上,提出杈式折流栅支撑结构,用来替换杆式折流栅,以进一步强化壳程传热效率,克服低流量下,折流杆换热器换热能力较差的局限。采用试验和数值方法考察杈式折流栅对换热器壳程流场和温度场的影响,得出最佳结构参数,以探究杈式折流栅换热器的适用工况范围。研究结果与结论可为管壳式换热器的优化升级和更高效的能源利用提供参考。
1 计算模型与数值方法
1.1 几何模型的构建
杈式折流栅固定安装在管壳式换热器的壳程中,由一个圆环和两组折流片构成,其换热器的整体模型如图1所示。

图1 杈式折流栅在管壳式换热器中的安装示意Fig.1 Schematic installation diagram of branch baffles in shell-and-tube heat exchanger
换热器筒体内的几何结构具有周期性,建立周期性全截面模型来研究其壳程性能,如图2所示,计算模型的主要结构参数列于表1。

图2 杈式折流栅换热器周期性全截面简化模型Fig.2 Periodic full section simplified model of branch baffle heat exchanger

表1 计算模型的主要结构参数Tab.1 Main structural parameters of the computational model
1.2 网格划分与边界条件设置
计算域选用非结构化四面体网格,对管壁划分边界层网格。网格数约370万,传热系数和压降的相对偏差分别为0.41%和0.28%,表明获得了网格无关解。利用CFD数值模拟软件FLUENT对湍流流动和传热进行数值模拟,湍流模型采用标准k-ε模型。以液态水为壳程介质,模型前后面为周期性边界条件,质量流量入口,流体进口温度设置为20 ℃,出口为压力出口。换热管壁温为70 ℃恒温,筒体内壁表面和折流栅壁面均为绝热,不可渗透及无滑移边界条件。在压力-速度的耦合中应用SIMPLE算法进行求解,二阶迎风格式用于离散动量和能量方程。为了保证壳程流体处于完全湍流的流动状态,所研究的雷诺数Re介于6 700~20 000之间,Re的定义为:
(1)
(2)
式中,Re为壳程雷诺数;ρ为流体密度,kg·m-3;u为壳程流体平均流速,m·s-1;de为当量直径,m;μ为整体温度下流体的动力黏度,Pa·s;Lt为换热管中心距,mm;do为换热管外直径,mm。
1.3 试验系统与试验验证
换热器试验模型示意如图3(a)所示,材料为有机玻璃。考虑到激光器的折射,将换热器壳体制作成长方体,换热管外径为19 mm,管中心距为30 mm,折流片定向角为45°,使激光能够方便地聚焦在测量位置。根据试验模型的大小等比例建立数值模型并进行计算。试验装置和试验系统流程图分别如图4,5所示。
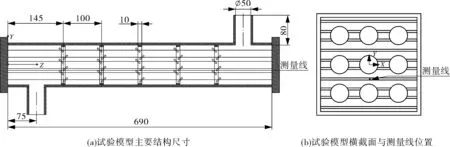
图3 试验模型尺寸与测量线位置Fig.3 Main parameters of the experimental model and location of the measurement line

图4 试验装置Fig.4 Experimental setup diagram
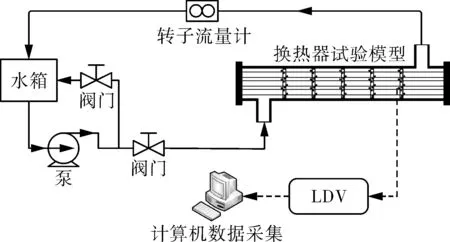
图5 试验系统流程图Fig.5 Experimental system flow chart
水箱中以自来水作为循环工质,其中添加空心玻璃珠作为示踪粒子,在室温下,使用激光多普勒测速仪[15-17](LDV)捕捉跟随流体流动的示踪粒子,利用Flowsizer软件采集试验数据。通过LDV对测量线上的多个特定点位进行测量,得到了每个测量点在z轴的速度分量。测量线位于(0,-15 mm,0)~(0,-15 mm,690 mm),介于第1排换热管与第2排换热管的中间,与换热管平行,如图3(b)所示。
图6示出了进口流量为4.5 m3/h时,试验数据与模拟数据的对比,可以看出,数值模拟结果与试验数据吻合较好,主流速度的平均误差和最大相对误差分别为7.71%和19.07%;数值结果与试验结果都表现出明显的周期性,且趋势一致,可以判断,数值模拟方法是准确的。

图6 数值模拟结果与试验结果的对比Fig.6 Comparison of numerical simulation values with experimental results
2 数据处理与结果分析
2.1 折流片定向角θ的影响
图7示出了5种不同折流片定向角θ的换热器传热系数h随Re的变化情况。当θ一定时,Re越大,h就越大。Re相同时,θ在30°~60°的变化区间内,h随θ的减少,先增大后减少,θ=37.5°时达到最大值。这是由于θ直接影响到流速的y轴速度分量,y轴速度分量增大,有利于削减热管边界层厚度,强化换热性能。可是,当θ过小时,左侧的折流片阻挡了流体的流动,削弱了右侧折流片的导流作用,因此,h不升反降。

图7 折流片定向角对壳程传热系数的影响Fig.7 Influence of orientation angle of the baffles on heat transfer coefficient
折线之间的高度差代表着h的相对增量,由图7可以看出,θ从60°减少到45°这一过程,h显著提高;继续减小到θ=30°,折线之间的间距收窄,在这期间h的变化并不明显。这就意味着,定向角小于45°后,继续减少夹角将不再是提高壳程传热系数的首选强化换热方案。
图8示出了5种不同折流片定向角θ的换热器压降Δp随Re的变化情况。可以看出,在θ一定时,Re越大,Δp也就越大;Re相同时,θ在30°~60°的范围内,Δp随θ的减小而增加。

图8 折流片定向角对壳程压降的影响Fig.8 Influence of orientation angle of the baffles on shell-side pressure drop
使用性能评价标准(performance evaluation criterion,PEC)反映换热器的整体综合性能,表示如下[18]:
(3)
(4)
(5)
式中,Nu为Nusselt数;f为阻力系数;h为壳程对流传热系数,W·m-2·K-1;λ为导热系数,W·m-2·K-1;Δp为壳程压降,Pa·m-1;L为换热管的长度,mm。
不同折流片定向角θ的换热器PEC数随Re的变化曲线,如图9所示。不同θ的换热器PEC数与Re呈正相关。θ=45°一直是最佳的折流片定向角配置参数。也就是说,在文中研究范围内,杈式折流栅的最佳折流片定向角与雷诺数无关。为了进一步提升换热器的壳程性能,以下选择θ=45°时,将折流栅间距设置为40,70,100,130,160 mm,进行分析。

图9 不同折流片定向角的换热器综合性能与Re的关系Fig.9 Relationship between comprehensive heat exchanger performance and Reynolds number at different orientation angles
2.2 折流栅间距Lb的影响
为了更好地解释折流栅间距对整体的影响,引入无量纲间距η,表示折流栅间距与壳内径的比,其定义为:
(6)
式中,Lb为折流栅间距;D为壳内径,D≡204 mm,则折流栅间距160,130,100,70,40 mm无量纲化后,分别为0.784,0.637,0.49,0.343,0.196。
图10示出了5种不同折流栅间距Lb的换热器传热系数h相对于Re的变化情况。当Re在6 700~20 000的范围内,5种换热器的h均呈现出上升趋势。在相同Re时,无量纲间距η越小,h就越大。减小折流栅间距与壳内径的占比,可以增强管壁和壳壁附近的湍流和速度波动,传热系数因此增加。

图10 折流栅间距对壳程传热系数的影响Fig.10 Influence of baffle spacing on shell-side heat transfer coefficient
图11示出5种不同折流栅间距Lb的换热器压降Δp相对于Re的变化情况。

图11 折流栅间距对壳程压降的影响Fig.11 Influence of baffle spacing on shell-side pressure drop
从图11可以看出,Re在6 700~20 000的范围内,5种换热器的Δp也都呈现出相同的上升趋势。在相同Re下,压降随着Lb的缩短而变大。折线之间的高度差代表着相对压降的增量,随着η的缩小,Δp的增幅越来越大。当η小于0.343后,Δp急剧上升,这就意味着,过分缩短的Lb将大幅增加流动阻力,对换热性能的负面影响也将成倍增加,因此,可以推测出杈式折流栅之间的距离如果小于壳内径的34.3%,综合性能可能会下降。
不同折流栅间距的管壳式换热器PEC数随Re的变化曲线,如图12所示。5种换热器的PEC数随Re的增大而增大。在相同Re下,随着Lb从160 mm缩短到40 mm,PEC数先增加后减少。当Lb=40 mm时,η=0.196,此时缩短间距带来的强化换热作用无法抵消显著增长的流动阻力对综合性能产生的负面影响,换热器的综合性能大打折扣,这个结果与之前的猜测相吻合,因此,建议杈式折流栅之间的间距大于壳内径的19.6%。Re大于10 000后,Lb=70 mm的换热器综合性能超过Lb=100 mm的换热器,成为最佳的折流栅间距配置参数,此时η=0.343。这些结果为合理设计及选择折流栅的结构参数提供了依据。

图12 不同折流板间距的换热器综合性能与Re的关系Fig.12 Relationship between comprehensive heat exchanger performance and Reynolds number at different baffle spacings
基于杈式折流栅换热器的数值计算结果,采用最小二乘法,通过多元线性回归[19]处理数据,给出了Re在6 700 ~ 20 000范围内,壳程传热和压降的经验关联式:

(7)
式中,Pr为流体普朗特数;μ,μw为流体特征温度和换热管壁温下的动力黏度,Pa·s。
(8)
以上两个经验关联式的适用范围为:Re=6 700~20 000,θ=30°~60°,Lb=40~160 mm。
2.3 与折流杆换热器的对比
2.3.1 壳程传热系数、压降、综合性能分析
由上述得出,当Lb=70 mm,θ=45°时,杈式折流栅换热器的壳程综合性能整体最优,采用该参数下杈式折流栅换热器与折流杆换热器进行比较。对相同折流栅间距下,折流杆直径为5 mm的折流杆换热器进行数值模拟,对比两者的壳程性能的差异。图13示出两种换热器之间的壳程性能曲线的对比。随着入口质量流量M的增加,两种换热器的壳程传热系数h和压降Δp都随之提升。M相同时,杈式折流栅换热器的h是折流杆换热器的2.7~3.0倍,Δp提高了14.2~18.5倍。
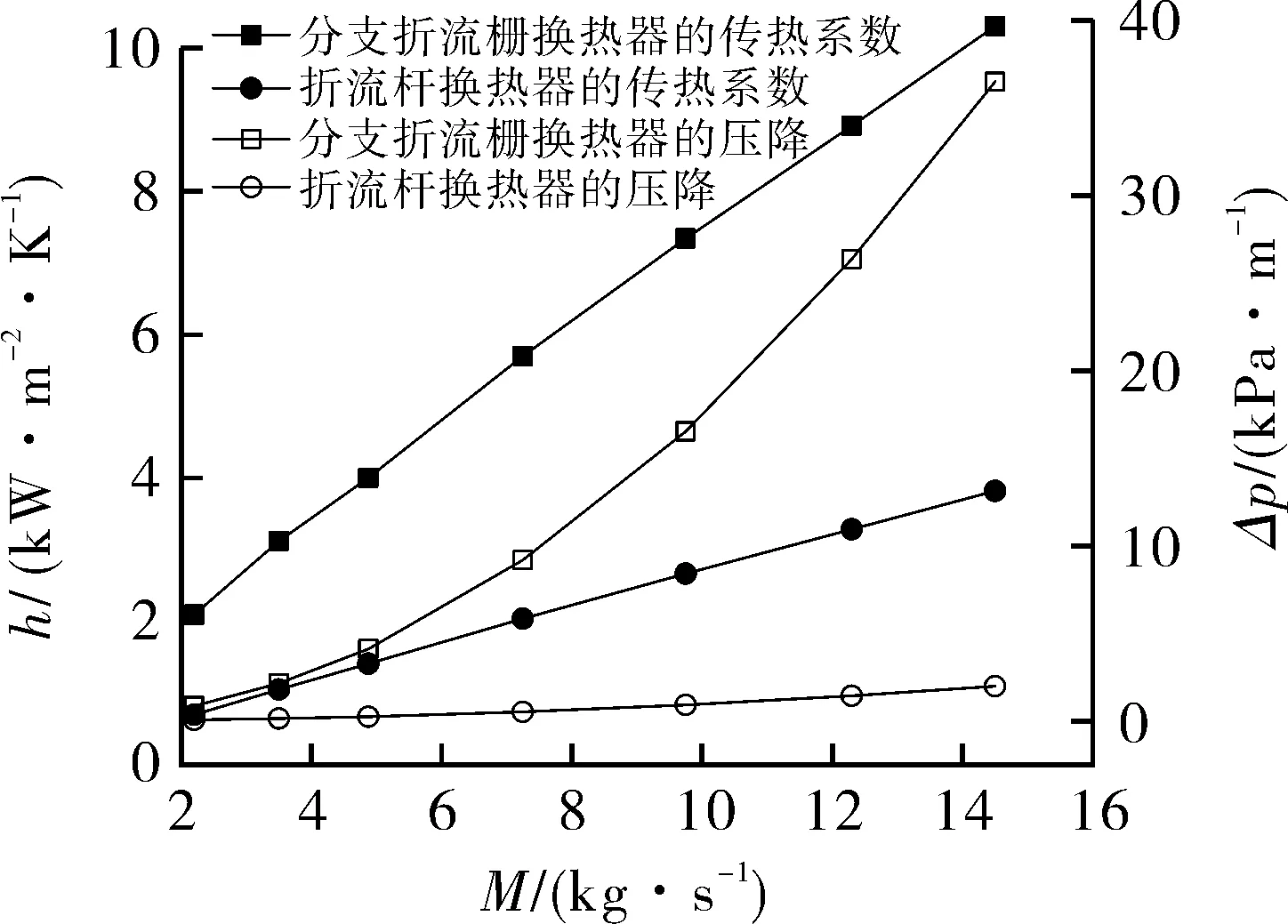
图13 两种换热器壳程性能的对比Fig.13 Comparison of the shell-side performance of two kinds of heat exchanger
以折流杆换热器作为参照对象,选用热性能因子[20](The thermal performance factor,TEF)对换热器进行比较,其定义为:
(9)
式中,Nu,f为杈式折流栅换热器的壳程Nusselt数和阻力系数;Nu0,f0为折流杆换热器的壳程Nusselt数和阻力系数。
图14示出了TEF随入口质量流量M的变化曲线。M介于2.2~14.5 kg·s-1之间,此时的Re介于3 000~20 000之间,TEF最小为1.021,最大值为1.240,意味着考察范围内,杈式折流栅换热器的综合性能比折流杆换热器提高2.1%~24.0%。TEF变化曲线随M的增加呈下降趋势,且斜率逐渐变缓,说明杈式折流栅支撑在较低雷诺数下,换热优势更加突出,可以弥补折流杆换热器低雷诺数下换热效果的不足。

图14 TEF数与入口质量流量的关系Fig.14 Relationship between TEF number and inlet mass flow rate
2.3.2 壳程流动特性对比
图15示出M=9.75 kg·s-1时,杈式折流栅换热器和折流杆换热器的壳程速度流线分布。在折流杆换热器中,壳程介质呈纵向流动,流动方向没有明显变化,具有一定降低流阻和抑制管束振动的优势[21],但折流杆的扰流作用较弱,壳程流速较低,传热能力不足;在杈式折流栅换热器中,壳程流体呈现出斜向和纵向混合流动,由于贴壁射流的作用,介质从折流片之间的间隙射出,流动速度明显增加,并快速发展为紊流,有助于强化对热管表面的冲刷动量,促进介质与热管相互作用后的局部混合,有利于强化换热性能。壳程流速分布与杆式折流栅支撑相比,流动速度明显增加,但是右侧折流片后存在一定的低流速、漩涡区域,将在以后的工作中考虑其影响。

图15 两种换热器的壳程速度流线分布Fig.15 Shell-side velocity streamline distribution of two types of heat exchanger
3 结论
本文建立了杈式折流栅换热器和折流杆换热器的周期性全截面模型,对其壳程流体流动和传热进行数值研究,加工了装配杈式折流栅的管壳式换热器的试验模型,并使用LDV验证了数值模型的准确性。得出以下结论。
(1)随着折流片定向角的减小,传热系数先增大、后减小,压降则不断增大,综合性能先增大、后减小。随着雷诺数的改变,杈式折流栅最佳的折流片定向角均为45°,与雷诺数无关。
(2)随着折流栅间距的减小,传热系数和压降同步增大,但综合性能表现出先增大、后减小的趋势。最佳折流栅间距与雷诺数有关。当无量纲间距小于19.6%后,综合性能显著下降,因此建议折流栅之间的距离大于壳内径的19.6%。
(3)紧凑的杈式折流栅支撑使换热器壳程流体呈斜向流和射流混合流动,增大了壳程介质扰动程度,强化局部卷吸,流体可以很快地进入充分湍流状态,对流换热强度随之提升。与折流杆换热器相比,相同质量流量下,杈式折流栅换热器的具有较高的壳程传热系数与压降,综合性能提高了2.1%~24.0%,尤其是在低流量下,换热效率的提升更为明显。
