角接触球轴承热特性研究
2021-09-24安佳琦张义民李铁军
安佳琦, 张义民, 李铁军
(沈阳化工大学 装备可靠性研究所, 辽宁 沈阳 110142)
滚动轴承与滑动轴承相比,具有结构简单、启动灵活、摩擦阻力小、维护简便、易于互换等特点,因而被广泛应用.在实际工况中,轴承的发热主要来源于各部件工作中的摩擦.摩擦将会导致轴承系统的温升以及热变形,进而对轴承的传动精度方面产生一定的影响,影响工作质量和效率.轴承承受的外载荷、转速的高低以及润滑方式等都会对轴承发热有一定的影响.因此,针对轴承不同工况下的发热情况进行研究具有重要意义[1-2].文献[1]用有限元方法分析了球轴承的稳态温度场.文献[3]运用ANSYS的APDL语言,建立了高温滚动轴承参数化建模与有限元分析系统,通过分析高温场下轴承的热变形和热位移规律,为轴承的加工精度设计提供了参考依据.文献[4]对层流状态下的液体动静压油膜轴承模型进行了数值仿真,并利用有限元软件ANSYS计算了轴承的热变形.文献[5]模拟仿真了静压推力轴承系统的热变形,得出其变形分布规律及油膜润滑性能预测模型,并通过试验得到验证.文献[6]基于轴承分析的拟静力学理论,考虑了轴承内部摩擦功耗生热和轴承零件的热变形,分析了不同工作转速和载荷下各节点温升导致的轴承零件的热变形,得出了轴承动态特性和热特性之间的耦合关系模型,并分析研究了轴承内部的动力学特性.本文利用ANSYS Workbench建立轴承瞬态热结构分析模型,分别在不同转速和轴向力的工况下对轴承进行仿真分析,探索二者对轴承温升和热变形的影响,以期为轴承温升导致的游隙变化提供分析方法.
1 有限元热分析模型
以25TAC62B角接触球轴承为例,利用ANSYS Workbench建立轴承瞬态热模型.轴承模型参数如下:公称外径为62 mm,公称内径为25 mm,外圈内径为51.57 mm,内圈的外径为37.37 mm,滚动体直径为6.9 mm,轴承宽度为15 mm;滚动体数目为18个,名义接触角60°;轴承外表面和空气对流传热系数取h=12 W/(m2·K).角接触球轴承几何模型如图1所示.根据Burton和Staph[7]提出的观点,轴承产生的摩擦热50 %传到滚动体上,50 %传到套圈上,分别在轴向力为500 N的不同转速工况下以及转速为4000 r/min的不同轴向力工况下,根据式(1)计算不同时刻轴承的发热率,然后通过施加发热率到轴承模型进行仿真分析.

图1 角接触球轴承ANSYS Workbench的几何模型
近似发热率
Q=2πMn/60.
(1)
总摩擦力矩M=M0+M1,
黏性摩擦力矩
载荷摩擦力矩M1=f1Pdm.
式中:f0—与轴承类型和润滑方式有关的系数;
v—工作温度下润滑剂的运动粘度mm2/s;
n—轴承的工作转速r/min;
dm—轴承直径 mm;
f1—与轴承结构和载荷有关的系数;
P—轴承所承受载荷N.
2 仿真分析
2.1 温度场分析
对施加热流的轴承构造一条由轴承外圈穿过球到达内圈的路径,10 min时的温度分布云图如图2所示.
图3给出了轴向力为500 N、不同转速下的轴承内外圈及滚动体的温升变化.当未达到热平衡时,随着时间的延长,转速从2000 r/min增加到8000 r/min,轴承内外圈和滚动体的温度逐渐升高,转速越快,温升越快;9 h左右温度逐渐稳定,温升很微小,逐渐达到热平衡,温度不再增加.

图2 轴承温度分布云图
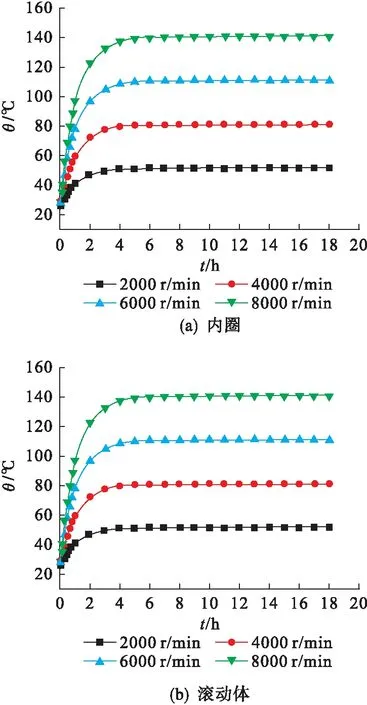
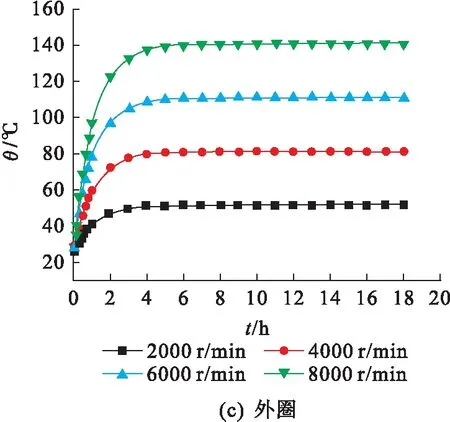
图3 轴向力为500 N时不同转速下轴承内外圈及滚动体温升变化
图4给出了转速为2000 r/min、不同轴向力下的轴承内外圈及滚动体的温升变化.由图4可知:当未达到热平衡时,随着时间的延长,轴向力从500 N增加到2000 N,轴承各部件温度也随之升高,轴向力越大,温升越快;9 h左右温度逐渐稳定,温升很微小,轴承逐渐达到热平衡,温度不再增加.

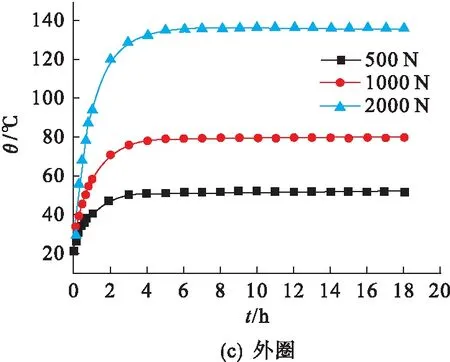
图4 转速为2000 r/min时不同轴向力下轴承内外圈及滚动体温升变化
2.2 热变形分析
图5给出了轴向力为1000 N、不同转速下的轴承内外圈及滚动体的热位移.
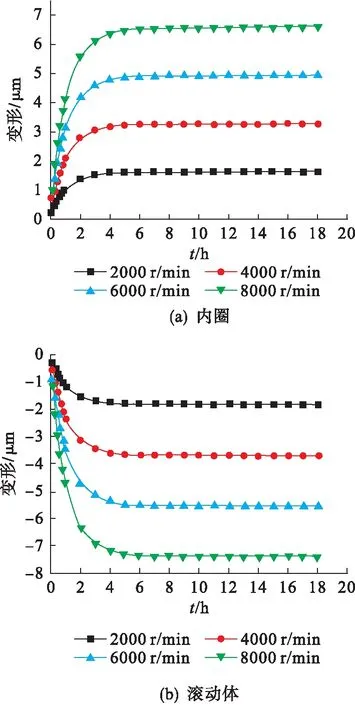

图5 轴向力为1000 N时不同转速下轴承内外圈及滚动体径向热位移
由图5可知:当未达到热平衡时, 随着时间的增加,内外圈以及滚动体的热变形逐渐增大,转速从2000 r/min增加到8000 r/min,轴承各部件热变形也随之增大,转速越快,热变形越大;到8 h左右,轴承逐渐达到热平衡,热变形开始稳定在一定数值;内圈变形量为正,表示内圈受热向外圈方向膨胀;滚动体和外圈变形量为负,表示滚动体和外圈受热向内圈方向膨胀.
图6给出了转速为4000 r/min、不同轴向力下的轴承内外圈及滚动体的径向热位移.
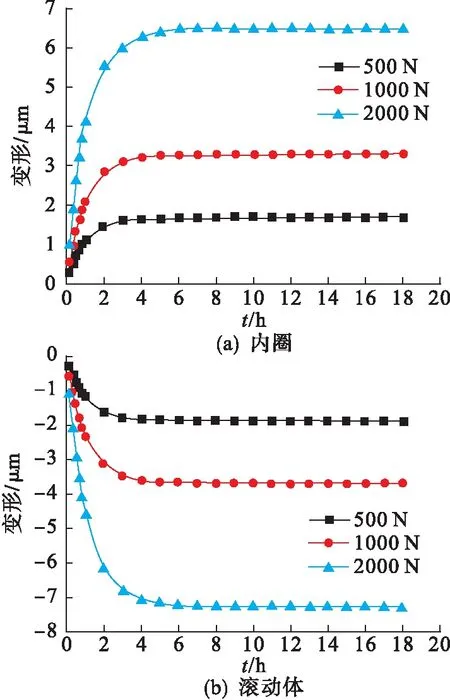

图6 转速为4000 r/min时不同轴向力下轴承内外圈及滚动体径向热位移
由图6可知:未达到热平衡时,随着时间的增加,内外圈以及滚动体的热变形逐渐增大;轴向力从500 N增加到2000 N,轴承各部件热变形也随之增大,轴向力越大,热变形越大;到8 h左右,热变形开始趋于稳定.
在轴向力1000 N、转速1500 r/min条件下,使用文献[8]的热网络法逆向辨识计算了轴承外圈的温度,结果如图7所示.

图7 轴承外圈温度仿真结果与逆向辨识结果对比
通过对比分析发现仿真结果与逆向辨识的结果基本一致.本文基于轴承热结构的瞬态分析模型的有效性得到验证.该模型不仅可以分析不同工况下轴承轴向和径向游隙随温升的变化,而且还可以进一步分析内外圈与滚动体接触区域的变化,为接触刚度变化等特性提供理论依据.
3 结 论
(1) 当未达到热平衡时,随着时间增加,轴承各元件温度逐渐升高.轴承转速一定时,随着轴向力的增加,轴承温度逐渐升高,达到热平衡时,温度稳定不再增加;轴承轴向力一定时,随着转速的增加,轴承温度逐渐升高,当达到热平衡时,温度保持稳定不再增加.
(2) 当未达到热平衡时,随加时间增加,轴承各元件热变形均在增大.轴承转速一定时,随着轴向力的增加,轴承热变形逐渐增大,达到热平衡时变形不再增加;轴承轴向力一定时,随着转速的增加,轴承热变形逐渐增大,达到热平衡时变形不再增加.内圈受热向外圈方向膨胀,滚动体和外圈受热向内圈方向膨胀.
(3) 利用有限元建立了轴承瞬态热结构分析模型,分别在不同转速和轴向力的工况下对轴承进行了仿真分析,探索了二者对轴承温升和热变形的影响,为轴承温升导致的游隙变化提出数值计算方法,为轴承热特性的研究提供了理论依据.
