独立学院大学数学课程混合式教学改革新探索

李璇

【摘要】本文主要探讨独立学院大学数学课程混合式教学改革的思路.首先，探讨课程设计的改革，如在课程教学中采用模块化教学、案例教学;其次，探讨实践教学环节的改革，如增设大学数学实验课程、融入数学建模思想;再次，探讨考核方式的改革，如在考核中加入“小论文”以完善质量评价体系;最后，给出线上教学改革的几点想法.

【关键词】混合式教学改革;模块化教学;案例教学;数学实验

一、引 言

高校向社会输送人才的质量直接取决于高校教育体系的教学效果.传统的高校数学教学模式已经不能满足现代高校对于人才素质教育的需要，高校大学数学课程改革迫在眉睫.专家们研究探索出適用于独立学院大学数学课程教学的实施步骤，并在不断实践中完善方案.只有这样才能真正有助于实现应用型人才培养目标.本文将探讨独立学院大学数学课程混合式教学改革的思路，主要分为四个方面：课程设计的改革、实践教学环节的改革、考核方式的改革、线上教学的改革.

二、混合式教学改革思路

（一）课程设计的改革

教学过程中的课程设计，由传统的教学模式转变为模块化教学，教师在教学中大量引入合适的案例，重视数学理论基础知识与专业课程学习的结合.

1.模块化教学

目前高等院校数学基础课程的教学，有的院校是按照一门课程的整体模式组织教学的，也有一些院校进行了模块化（专题化）设计与教学.在应用型本科院校中，不同的专业对学生数学能力的要求不尽相同，教师应结合学生的就业目标，重视所教课程的应用，进行模块化教学改革.

（1）分专业制定模块化教学的内容.传统的数学教学模式是所有专业共用同一本《高等数学》教材，教师授课是按照课本章节进行的，在这样的教学模式下学生体会不到学习数学的乐趣，他们会认为数学仅是枯燥的公式推导.教师在分专业制定模块化教学内容时，可以适当删除与专业无关但不影响培养学生计算和思维能力的内容，删减的同时还要在教学内容中添加与本专业相关的实际案例，为学生后续的专业课学习打好基础.与此同时，教师要修改旧有的教学大纲，同一门数学课程但面向不同专业将会对应不同的教学大纲.

（2）具体的模块化的教学设计.具体的模块化的教学设计分为三个模块：基础知识模块、应用模块、能力提升模块.学生通过基础知识模块的学习和训练掌握最基础的数学知识、数学思维方法及一些计算工具，为后续学习数学类其他课程及专业课程提供一定的数学储备.应用模块主要是将数学知识与专业课相结合，重视数学实验，引入数学建模.学生通过应用模块的学习能应用所学数学理论知识解决专业课中的一些实际问题，在解决具体问题的过程中体会学习数学的乐趣.能力提升模块主要包括每门数学课程在基础知识模块中没有讲的但数学竞赛或者研究生考试有要求的内容，教学难度有所提高，知识面更广.经过这个模块的学习，基础较好的学生可以加深其对数学知识的进一步理解，那些有升学需求的学生也可以得到帮助.以教授天津财经大学珠江学院《微积分》课程为例，根据课程内容的逻辑关系，基础知识模块可分为：（1）极限与连续，（2）一元函数微分学，（3）一元函数积分学，（4）多元函数微分学，（5）多元函数积分学.应用模块可设计为：（1） 导数在经济中的应用，（2）积分在经济中的应用.能力提升模块因为有一定的针对性，所以院校可以将其作为选修课，教师在授课时可补充微分方程、级数等内容.

2.案例教学

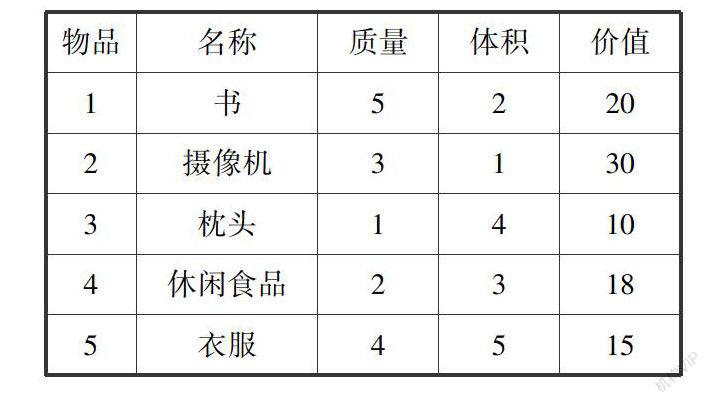
案例教学是将理论知识与实践相结合的一种教学模式，有助于学生更直观地感受到所学课本知识在实际生活中的应用，从而调动学生学习的积极性.以《概率论与数理统计》课程为例，该课程内容相对丰富，理论性强，在生活中应用广泛.教师在授课中可以选取一些经典案例，使学生加深对知识的理解，例如，在讲二项分布这一章节时，教师可以选取日常生活中大家都很熟悉的“相亲大会”的例子：假设你在相亲大会上能够牵手心仪的他（她）的概率只有1%[WTBX]，那么你最终至少成功一次，需要相亲多少次呢？再比如《运筹学》课程，其涉及大量的建模公式，教师在授课中可以采用案例教学使学生理解教学内容，在讲整数规划时，可引用我们日常生活常见的背包问题，通过实际问题的建模加深对整数规划应用的理解.案例如下：

（二）实践教学环节的改革

目前我国一些独立学院开设的数学类课程包括微积分、高等数学、线性代数、概率论与数理统计、离散数学等，并未开设数学实验课程，考虑到应用型本科院校注重理论知识与实践的结合，独立学院应增设大学数学实验课程，使教师在教学中融入数学建模思想，这将有助于提高大学数学教学的有效性.大学数学实验课程的教学主要是通过应用数学实验软件解决实际问题，学生在实验过程中通过自主分析、研究解决问题的方法，提高自己的数学思维能力及应用能力.将数学实验融入其他数学课程中，利用数学软件辅助大学数学的教学，是实践教学改革的进一步深化.如在《线性代数》中，面对复杂行列式的求解、逆矩阵的求解，我们完全可以用Mathematica软件来解决，常用命令Det来求行列式，Inverse来求逆矩阵等.

数学实验课程的开展，首先，有利于提高大学数学课程的课堂教学效率，例如复杂行列式的计算需要消耗学生大量的计算时间，但应用计算机软件问题可能几秒就被解决;其次，学生会从中体会到数学实验的实用性，这将有助于提高他们学习的兴趣，他们开始将“学数学”变为“做数学”，开始将数学思想引入实际问题中;最后，会提高独立学院参与数学建模竞赛的能力，学生熟练掌握数学软件对于解决建模问题大有好处.

（三）考核方式的改革

教学改革的深入需要与其相对应的新的考核方法，传统的大学数学的考核方法通常是以平时成绩和期末成绩构成的总的质量评价标准，但此种考核并没有体现学生的数学应用能力.为此，我们希望在改革中增设小论文，由教师在一学期结束后给出具体的实际应用题目，学生可以根据自己所学数学知识，也可应用数学软件，充分发挥自主性，探究应用题的解决方案，最终形成论文上交.例如，教师在结束了一学期的《运筹学》课程之后，可以让学生写一篇能够体现运筹学知识在管理经济中应用的论文，就某一方面（线性规划、运输问题、整数规划、图与网络）在经济管理中的应用展开论述和研究，题目可自拟.这样的题目可激发学生的学习动力，他们会积极地将所学运筹学知识与经济问题结合在一起，并在解决问题中强化自己的运筹学知识.