极限状态模糊性对地震易损性分析的影响研究:以钢筋混凝土框架结构为例
2021-09-23于晓辉李越然宋鹏彦吕大刚
于晓辉,李越然,宋鹏彦,吕大刚
(1. 哈尔滨工业大学结构工程灾变与控制教育部重点实验室,黑龙江,哈尔滨 150090;2. 哈尔滨工业大学土木工程学院智能防灾减灾工业与信息化部重点实验室,黑龙江,哈尔滨 150090;3. 河北大学建筑工程学院,河北,保定 071002)
近年来,以风险为导向的新一代基于性能地震工程得到了研究人员的广泛关注[1]。根据美国太平洋地震工程研究中心(PEER)提出的全概率风险决策框架[2],地震风险分析被分解为3个基本模块,包括:地震危险性分析、地震易损性分析和地震损失分析。其中,地震易损性分析是连接地震危险性分析与地震损失分析的桥梁,它用来确定工程结构在不同强度地震作用下发生不同极限状态破坏的概率[3 − 4]。近年来,地震易损性被广泛应用于不同类型结构的地震安全评估中[5 − 9],已经成为工程结构地震安全评估的一种有效手段[10]。
地震易损性分析主要包括概率地震需求分析[11]和概率抗震能力分析[12]。其中,概率抗震需求分析用来建立地震动强度与结构响应之间的统计关系;概率抗震能力分析则用来定义不同极限状态对应的结构抗震能力限值的概率分布。结构极限状态的划分与结构损伤水平紧密相关,通常依赖于工程经验判断,无法形成较为统一的标准。仅以倒塌极限状态而言,如何来定义结构倒塌?不同的工程和研究人员对其定义均不同。因此,极限状态的定义具有很强的“模糊性”。鉴于此,如何衡量地震易损性分析中极限状态划分标准的模糊性,定量评价极限状态模糊性对地震易损性的影响是一个值得研究人员关注的问题。
早在1965年,美国著名的控制论专家Zadeh[13]率先提出了模糊集合(fuzzy sets)理论。其中,他提出采用“隶属函数(membership function)”来实现现象差异的中间过渡,这突破了经典集合论中属于或不属于的绝对关系,并由此开创了模糊数学学科。近年来,模糊数学在地震易损性的相关研究中已经得到了一定应用。例如:黄龙生和姜淑珍[14]基于历史地震资料,采用模糊综合评估方法,开展了群体公路桥梁的地震易损性分析,获得了公路桥梁的地震易损性矩阵。张桂欣和孙柏涛[15]提出了一种基于模糊层次分析的建筑物单体震害预测方法,并针对汶川地震中的若干结构震害数据进行了验证。何浩祥等[16]提出了一种基于多元模糊评定的桥梁综合地震易损性分析方法,实现了从桥梁单元易损性到桥梁体系易损性的过渡。Colangelo[17 − 18]通过引入模糊-随机模型,利用可靠度理论中的经典概率干涉方法,推导获得了考虑极限状态模糊性的地震易损性函数。然而,极限状态的模糊性与所采用的隶属函数紧密相关。采用不同类型的隶属函数去描述极限状态中存在的模糊性会导致地震易损性结果的不同。此外,极限状态模糊性对地震易损性函数参数的影响也缺乏定量的评估。
针对上述问题,本文采用10种不同隶属函数来表征极限状态定义中的模糊性,采用模糊-概率模型推导获得不同隶属函数对应的地震易损性解析函数,定量评价不同隶属函数对地震易损性函数的影响,给出考虑极限状态模糊性的地震易损性函数修正方法。为说明上述研究思路,以4栋不同高度和不同设防烈度的RC框架结构为例,进行应用分析。
1 基本概念
1.1 模糊集与隶属度
随机变量X上的一个模糊集A是指:对任何x∈X,均有一个数μA(x)∈[0,1]与之对应。其中,μA(·)被称之为模糊集A的隶属函数,又被称作模糊分布。μA(x)表示x对A的隶属度[19]。根据隶属度的定义,可知:当μA(x)=1时,元素完全属于模糊集A;μA(x)=0时,元素完全不属于模糊集A。图1给出了经典集合论与模糊集中关于隶属度的定义及其差异。由图1可见,在经典集合论中,代表点的隶属度非0即1。然而,在模糊集合论中,代表点对集合的隶属度是在[0,1]。
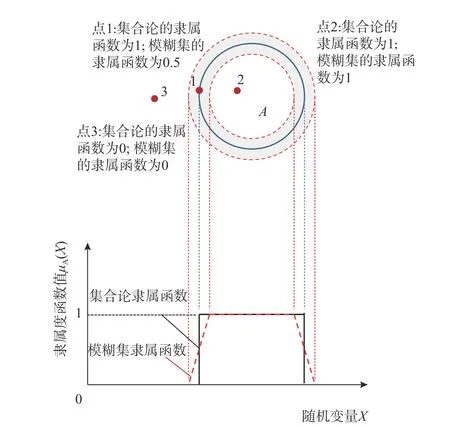
图1 经典集合论与模糊集合论中的隶属度含义差异Fig.1 Difference between memberships defined according to the classic sets and the fuzzy sets
1.2 隶属函数
确定隶属函数μA(·)的方法主要包括:统计实验法、指派法、借用(已有客观尺度)法、二元对比排序法等。本文采用指派法确定极限状态的隶属函数。指派法是一种基于检验并根据问题性质而直接采用典型隶属函数来模拟模糊性的方法。根据问题中所要描述对象的模糊性大小,所指派的隶属函数包括偏小型、中间型和偏大型,分别用来描述偏小、中间状态、偏大的模糊现象。
地震易损性分析中的极限状态定义包含大量工程经验,不同工程和科研人员对同一极限状态的理解也不尽相同,可认为属于模糊性较大的情况。因此,本文采用偏大型隶属函数来描述极限状态定义存在的模糊性。采用模糊-概率积分的方法在地震易损性分析中考虑极限状态模糊性,基本原理详见第2节。本文考虑了10种不同类型的偏大型隶属函数,如式(1)~式(10)所示。式中,α表示x的界限值;λ用来控制模糊区间的宽度。在所考虑的10种隶属函数中,µ2(x)、µ3(x)、µ4(x)为幂函数型,µ5(x)、µ6(x)、µ7(x)为三角函数型,µ8(x)为指数型,µ9(x)和µ10(x)为对数型。µ1(x)较为特殊,其在整个模糊区间上模糊度为0.5,表示其在整个模糊区间上模糊性均达到最大。图2给出了所考虑的10种隶属函数的模糊分布曲线,以[(1−λ)×α,(1+λ)×α]为模糊区间,且在x=α界限值处取得最大模糊值。为说明模糊性的影响,图2中以经典集合论中的非0即1的隶属函数c(x)(见式(11))作为对比。

图2 本文考虑的10种隶属函数Fig.2 Ten membership functions considered in this paper
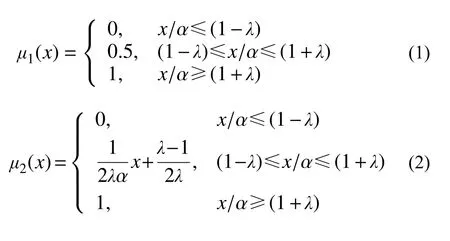


1.3 隶属函数的模糊度参数与形状参数
为了较为定量地衡量隶属函数之间的差别,本节特引入模糊度参数和形状参数分别来描述隶属函数的模糊度大小以及隶属曲线形状特点。模糊性大小与模糊区间大小紧密相关,而模糊区间大小则由参数λ(λ>0)来决定(即:[(1−λ)×α, (1+λ)×α]为模糊区间)。具体而言,λ越大,模糊区间范围越大,隶属函数曲线越平缓,表示x在界限周围的模糊性越大;λ越小,模糊区间范围越小,隶属函数曲线越陡,表示x在界限周围的模糊性越小。当λ=0时,指数型隶属函数µ2(x)、µ3(x)、µ4(x)与c(x)完全重合。这一结果表明:当λ=0时,隶属函数所表征的模糊性消失,隶属函数退化为经典集合论中非0即1的阶跃型隶属函数。综上,λ可视为隶属函数的模糊度参数。
为了更加全面地定量分析不同隶属函数对地震易损性函数的影响时,本文提出了一个反映隶属函数形状特性的变量γ,该变量能够反映隶属函数曲线在模糊区间[(1−λ)×α, (1+λ)×α]上的形状特征,如图3所示。γ的定义如式(12)所示:

式中: |μk(x)−c(x)|表 示隶属函数μk(x)与c(x)的差值;λα表示模糊区间(式(12)积分区间)的1/2,可计算为:[(1+λ) × α−(1−λ)× α]/2。因此,根据式(12)和图3,通过与c(x)对比,γ可以定量化反映隶属曲线形状的“陡峭”和“平缓”程度。γ值越大,说明μk(x)与c(x)相差越大,模糊区间越大,因此,说明隶属曲线形状越“平缓”。反之,隶属曲线形状越“陡峭”。根据γ的定义式,γ=0表示隶属函数与c(x)一致;γ=1表示隶属函数在λ区间上的函数值皆为0.5,此时隶属函数为µ1(x)。

图3 隶属度函数的模糊形状参数的定义Fig.3 Definition of fuzziness shape factor of membership functions
值得说明地是,λ和γ分别用来描述隶属函数的模糊度和形状特征,前者反映模糊程度大小,后者反映隶属函数形状特征。根据式(12),分别计算10种隶属函数µi(x) (i=1,2,···,10)的形状参数γ值,如表1所示。

表1 10种隶属函数的形状参数γTable 1 Calculated shape factors γ of ten membership functions
2 基于模糊-概率积分的易损性函数
2.1 模糊-概率积分的基本原理
根据经典的可靠度概率干涉理论,结构失效概率P可以表示为结构抗力R与结构需求S的卷积,可表示为:
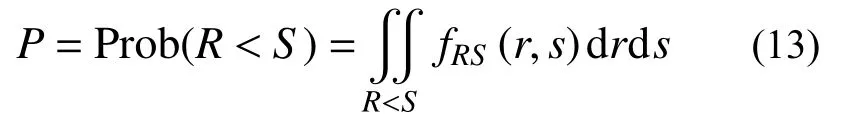
式中:fRS为R与S的联合概率密度函数;r和s分别为R与S的实现。
引入经典集合理论中的隶属函数c(x)(见式(11)),式(13)可表示为:

采用模糊集中的隶属函数μ(r,s)替换式(14)中的c(r,s),获得概率-模糊积分为:

式中,P′表示考虑模糊性的失效概率。
当λ=0时,式(14)和式(15)的解析表达式一致,即:P′=P。令R∗=lnR和S∗=lnS,式(15)改写为:

2.2 考虑模糊性的地震易损性解析函数
地震易损性函数F(x)可分为:基于地震动强度的函数和基于变形的函数[3]。其中,采用基于变形的地震易损性函数,可以将地震易损性分析分解为概率地震需求分析和概率抗震能力分析。式(17)给出了常用的基于变形的地震易损性函数:
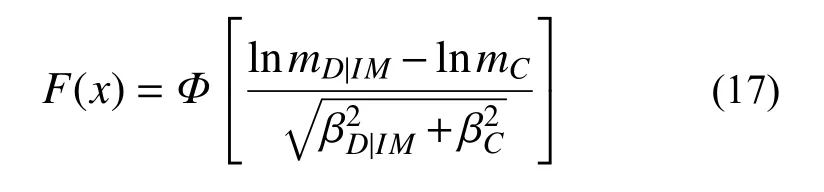
式中:mC和 βC分别表示对应不同极限状态的结构抗震能力C的中位值和对数标准差;mD|IM和βD|IM分别表示在给定地震动强度IM下,结构需求D的中位值和对数标准差,可分别按式(18)和式(19)计算[11]:
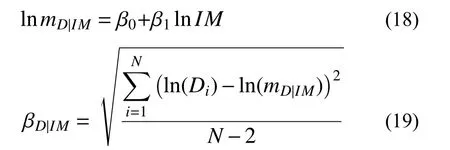
式中:Di(i=1,2,···,N)为第i条地震动作用下的地震需求;N为地震动个数;系数 β0和 β1要通过对数线性回归获得。
基于式(17),分别以C和D替换式(15)中的R和S,则有R∗=C∗和S∗=D∗。令t=C∗−D∗,则有D/C=e−t。将式(16)进行变换,得到:

根据式(20),可以推导获得采用前4类隶属函数μi(x)(i=1,2,3,4)来考虑极限状态模糊性的地震易损性解析函数。基于剩余6类隶属函数,无法利用式(19)直接获得考虑极限状态模糊性的地震易损性函数的解析表达式,需借助数值积分方法求解。
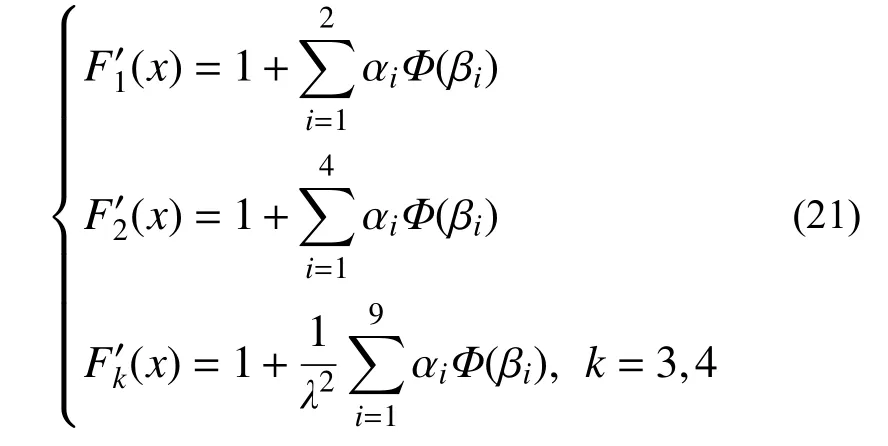
式中,系数αi和βi见表2。

表2 考虑极限状态模糊性的地震易损性函数系数Table 2 Parameters of seismic fragility functions considered limit state fuzziness
2.3 考虑模糊性的地震易损性函数数值积分
若式(20)无法获得解析解,可以采用蒙特卡洛法进行数值积分求解。将式(20)分解为2部分积分,第一部分积分域为 [ −ln(1−λ),0],假设t在区间 [−ln(1−λ),0]上服从均匀分布,概率密度函数为g(t),则有:



式(20)的第二部分积分域为 [0,ln(1−λ)],可表示为:

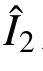
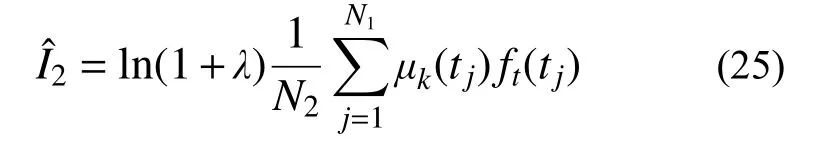
将式(23)和式(25)代入式(20)中,可以获得考虑极限状态模糊性的地震易损性的数值积分解为:
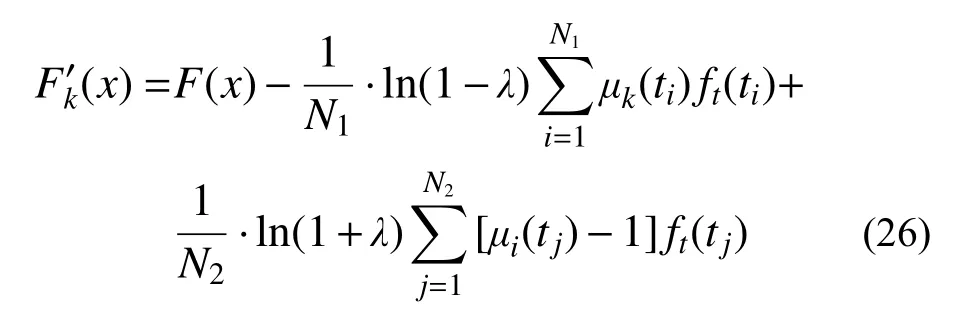
3 考虑极限状态模糊性的RC框架结构地震易损性分析
3.1 RC框架结构
本文选取文献[11]和文献[20]中所采用的4个不同高度且具有不同设防烈度的RC框架结构为例,分析极限状态模糊性对地震易损性的影响。这四个RC框架结构为:1) 结构F-1,3层结构,其设防烈度为VI度,设计基本加速度为0.05g;2) 结构F-2,5层结构,设防烈度为VI度,设计基本加速度为0.05g;3) 结构F-3,8层结构,设防烈度为VI度,设计基本加速度为0.05g;4) 结构F-4,10层结构,设防烈度为VI度,设计基本加速度为0.05g。采用OpenSees对结构在地震作用下的非线性反应进行分析。上述四个算例结构的设计和建模详细信息可参见文献[11]。为保证论文的完整性,给出四个框架结构的平面和立面布置,如图4所示[11]。

图4 算例结构 /mm Fig.4 Case structures
3.2 不考虑极限状态模糊性的地震易损性分析
值得指出地是,考虑极限状态模糊性的地震易损性分析,只需要在已有地震易损性分析结果基础上,利用第2节中基于模糊-概率模型推导获得的考虑极限状态模糊性的地震易损性解析和数值解,即可计算获得。因此,本文所提出的方法可以较为简单有效地利用已有地震易损性分析结果,无须额外进行地震时程分析,即可在传统地震易损性分析结果的基础上考虑极限状态模糊性的影响。
鉴于上述,由于文献[20]中已经较为详细地给出了上述四个RC框架结构的地震易损性分析过程和结果,因此,本节仅给出不考虑极限状态模糊性的地震易损性分析结果。其中,采用100条地震动作为输入,以谱加速度Sa作为地震动强度参数,以结构最大层间位移角θmax为地震需求参数,采用云图法[11]建立概率地震需求模型。结构的极限状态划分为4级:轻微破坏、中等破坏、严重破坏和完全破坏。采用随机Pushover方法[12]建立不同极限状态对应的概率抗震能力模型。表3和表4分别给出了上述四个RC框架对应的概率地震需求模型参数和概率抗震能力模型参数。将表中给出的需求和能力模型参数代入式(16),即可获得地震易损性曲线。

表3 概率地震需求模型参数Table 3 Probabilistic seismic demand model parameters

表4 概率抗震能力模型参数Table 4 Probabilistic seismic capacity model parameters
3.3 考虑极限状态模糊性的易损性分析
基于3.2节中不考虑极限状态模糊性的地震易损性分析结果,根据2.2节和2.3节中方法,获得考虑极限状态模糊性的地震易损性曲线。仅以一种隶属函数µ3(x)为例,给出四个算例结构在考虑和不考虑极限状态模糊性情况下的地震易损性曲线,如图5所示。由图5可见,考虑极限状态模糊性的地震易损性曲线要比不考虑极限状态模糊性的地震易损性曲线更为平缓。极限状态模糊性对完全破坏状态的地震易损性影响要高于其对其他三个状态地震易损性的影响。第4节将定量评价极限状态模糊性对地震易损性的影响,进一步讨论不同隶属函数描述极限状态模糊性对地震易损性的影响。
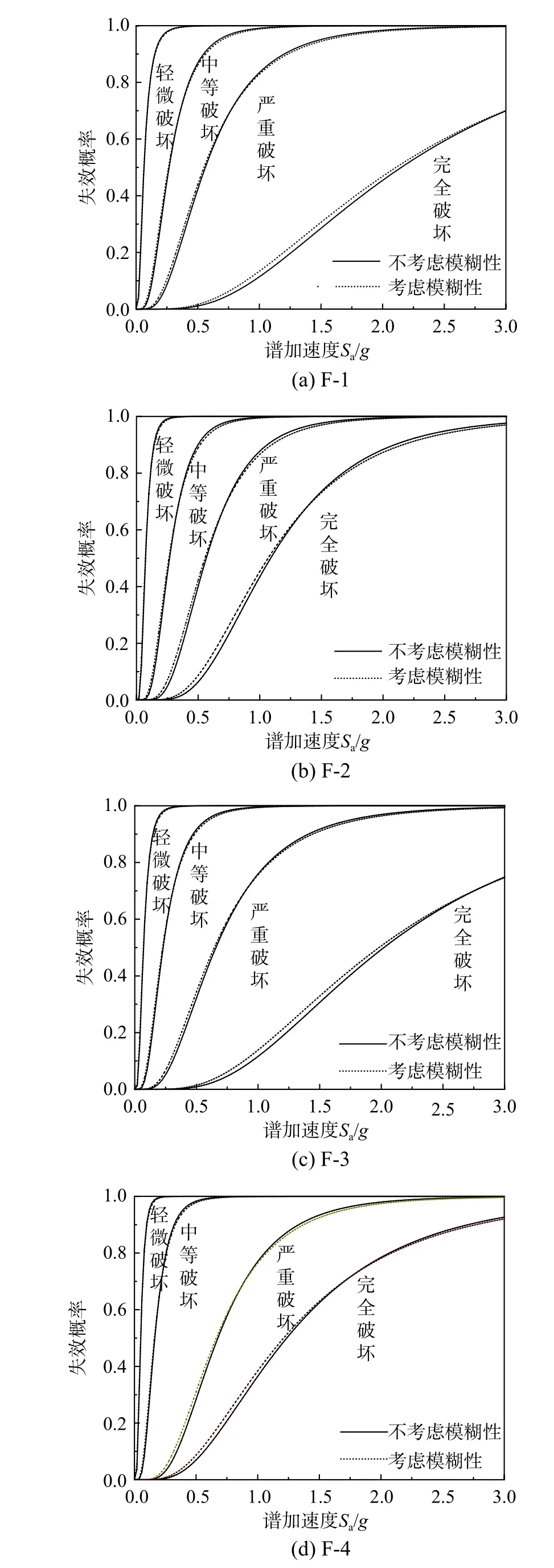
图5 考虑和不考虑极限状态模糊性的地震易损性曲线Fig.5 Seismic fragility curves with and without considering fuzziness in limit states
4 极限状态模糊性对易损性的影响
4.1 极限状态模糊性对易损性的影响系数
本文提出了一个影响系数 ηP来定量评价极限状态模糊性对地震易损性的影响,如式(27)所示:

式中,[0,xup]为积分区间,本文取xup=2.0g。对于谱加速度Sa而言,Sa=2.0g这一强度已足够大能使其对应的失效概率接近为1。因此,式(27)所示的积分可以对极限状态模糊性对地震易损性曲线在较宽区间内的影响给出评估; ΔPmax表示考虑和不考虑极限状态模糊性的地震易损性曲线的最大绝对概率差,可表示为:

4.2 极限状态模糊性大小的影响
仅以3层结构F-1为例,将结构在严重破坏状态对应的考虑和不考虑极限状态模糊性的地震易损性曲线进行对比,如图6所示。其中,采用隶属函数µ4(t)来描述极限状态模糊性,关注不同模糊度参数λ取值对地震易损性的影响。

图6 λ值对考虑极限状态模糊性的地震易损性的影响Fig.6 Effect of λ values on seismic fragility curves considering fuzziness in limit states
由图6可见,λ取值越小,考虑极限状态模糊性的地震易损性曲线与传统地震易损性曲线越接近。当λ增大时,考虑模糊性的易损性曲线趋于平缓,且逐渐偏离传统易损性曲线。当λ→0时,考虑模糊性的易损性曲线与传统易损性曲线基本重合。在实际地震易损性的相关研究中,λ的取值受研究人员主观因素影响较大。若研究人员认为所采用的极限状态定义存在较大的模糊性,可以取较大的λ值。反之,可以取较小的λ值。
4.3 隶属函数的影响
仍以3层结构F-1为例,采用不同隶属函数来描述极限状态模糊性,对比结构在严重破坏状态对应的考虑和不考虑模糊性的地震易损性曲线,如图7所示。仅研究隶属函数对地震易损性的影响,在此取λ定值为0.5。由图7可见,采用不同隶属函数获得的考虑模糊性的地震易损性曲线并不相同。为了定量评估隶属函数选择对考虑模糊性的地震易损性结果影响,采用ηP作为评价指标。图8给出了10种隶属函数对结构F-1、F-2、F-3和F-4在严重破坏极限状态时地震易损性结果的影响。由图8可以看出,随着γ的增大,不同隶属函数对易损性的影响也逐渐显著。综合图7的结果,在本文所考虑的隶属函数中,按照ηP的大小进行排序为:

图7 隶属函数对考虑模糊性的地震易损性的影响Fig.7 Effect of membership on seismic fragility considering fuzziness in limit states
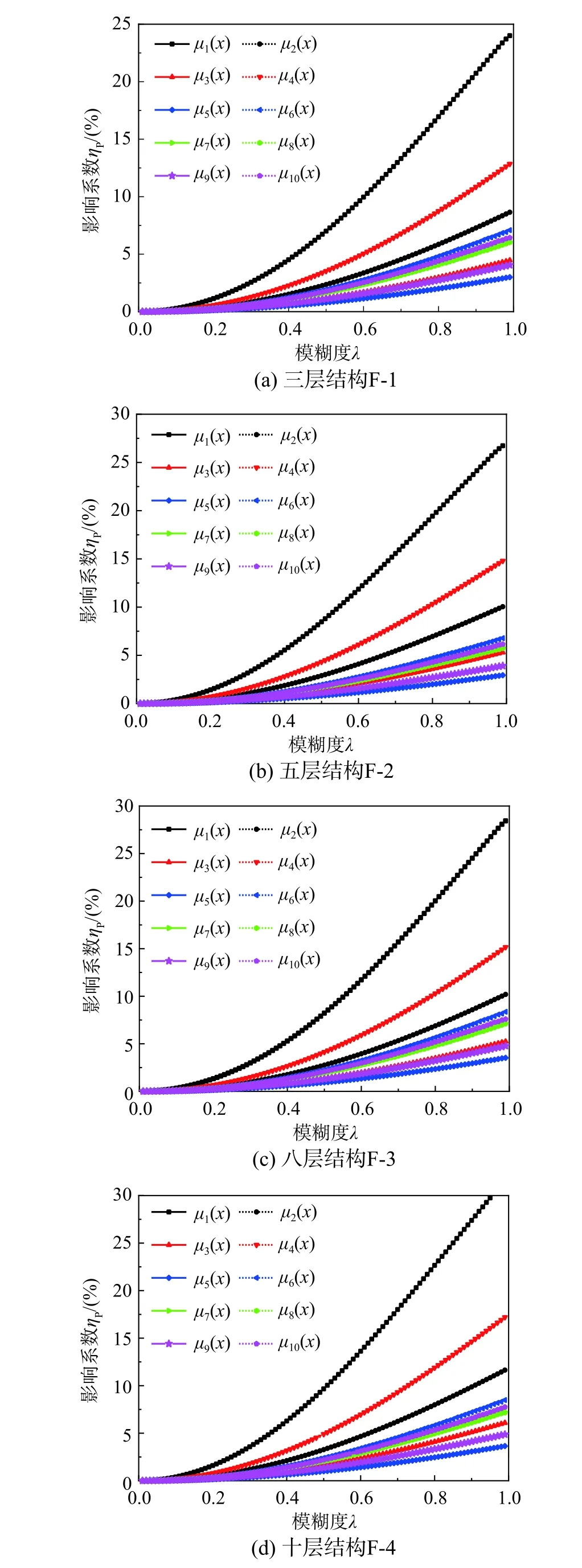
图8 10种隶属函数对应的ηP值及其随λ的变化Fig.8 Values of ηP corresponding to ten membership considered and the corresponding variation with λ
μ1(x)>μ4(x)>μ2(x)>μ6(x)>μ10(x)>μ8(x)≈μ7(x)>μ3(x)>μ9(x)>μ5(x)
将隶属函数形状对地震易损性结果的影响按ηP值大小分成5个等级,如表5所示。针对四个算例结构,计算10种隶属函数对地震易损性的影响等级。结果表明,对地震易损性影响较高的隶属函数为:µ1(x)、µ2(x)、µ4(x)和µ6(x)。随着λ值的增大,极限状态模糊性对易损性的影响等级显著增加,影响程度可以达到V级(ηP>15%)。对于其他隶属函数,当λ>0.7时,其对地震易损性的影响程度也较为明显,影响等级可以达到III级,5%<ηP<10%。综上,要合理考虑极限状态的模糊性,要综合考虑隶属函数和λ值的影响。

表5 基于ηP的隶属函数形状对地震易损性影响等级划分Table 5 Classification of effect of membership functions on seismic fragility curves using ηP
5 考虑极限状态模糊性的易损性修正
根据第2节,通过模糊-概率积分可获得考虑极限状态模糊性的地震易损性函数。但是,这种方法获得的地震易损性解析函数通常较为复杂。为解决这一问题,本文提出了一种较为简化的考虑极限状态模糊性的地震易损性函数修正方法。该方法基于模糊-概率积分法获得的地震易损性结果,假设考虑极限状态模糊性的地震易损性函数仍然服从对数正态分布,通过建立地震易损性函数中位值和对数标准差与模糊度参数λ之间的回归关系,实现极限状态模糊性对地震易损性函数的修正。
将式(18)代入式(17)中进行变换,获得基于地震动强度参数的易损性函数,如式(29)所示[3]:

式中,未考虑极限状态模糊性的地震易损性函数中位值mR和对数标准差 βR,按式(30)和式(31)计算:

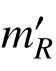

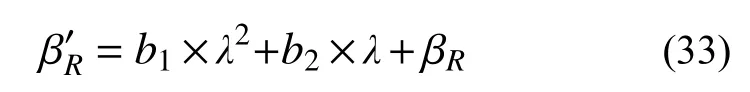
式中,a1、a2、b1、b2为回归参数,受隶属函数形状影响,不同隶属函数对应不同的回归参数。
修正后的地震易损性函数为:
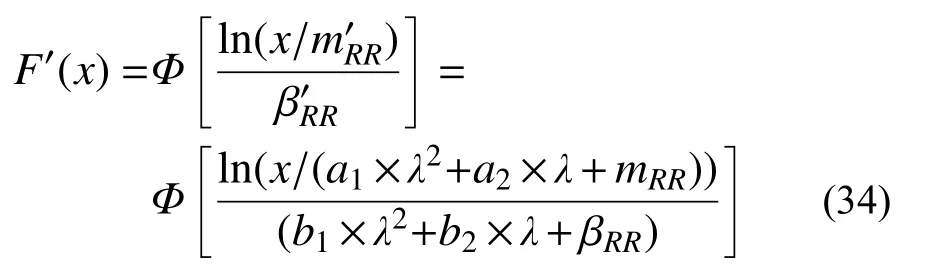


图9 和与λ的关系Fig.9 Relationships between and and λ
6 结论
本文考虑10种隶属函数来描述极限状态模糊性,考虑不同模糊度的影响,采用模糊-概率积分法推导了考虑极限状态模糊性的地震易损性函数。以4个RC框架结构为例,开展了考虑极限状态模糊性的地震易损性分析,研究了在极限状态模糊性中考虑不同隶属函数和不同模糊度对地震易损性结果的影响,给出了考虑极限状态模糊性修正的地震易损性函数。得到如下结论:
(1) 采用不同隶属函数考虑极限状态模糊性对地震易损性结果影响较为显著。随着模糊度的提高,不同隶属函数对应的考虑极限状态模糊性的地震易损性分析结果差异也逐渐增加。
(2) 在本文所考虑的10种隶属函数中,µ1(x)、µ4(x)、µ2(x)和µ6(x)对地震易损性的影响较大,在模糊度较大时(λ>0.7),极限状态模糊性对易损性的影响可以达到15%以上。对于其他隶属函数µ3(x)、µ5(x)、µ7(x)、µ8(x)、µ9(x)和µ10(x),当模糊度较大时(λ>0.7),极限状态模糊性对地震易损性的影响在5%~10%。
(3) 采用本文提出的考虑极限状态模糊性修正的地震易损性函数可以较好地体现极限状态模糊性对地震易损性的影响。
值得指出地是,考虑极限状态模糊性的地震易损性函数选取受研究人员主观意愿控制。若研究人员认为在地震易损性分析中所采用的极限状态模糊性较大,就可以选取较大的λ值,同时根据自己的经验去选取特定的隶属函数,并利用本文推导的相应的考虑极限状态模糊性的地震易损性函数进行分析。反之,研究人员可以选择较小的λ值或者不考虑极限状态的模糊性。但是,本文提供的考虑极限状态模糊性的地震易损性解析函数,为工程人员更加客观地考虑极限状态定义中存在的经验性问题提供了一条解决方案。
