几何与非几何相似试件确定混凝土韧度及强度
2021-09-23管俊峰姚贤华李列列胡圣能
管俊峰,鲁 猛,王 昊,姚贤华,李列列,张 敏,胡圣能
(华北水利水电大学土木与交通学院,河南,郑州 450045)
准确确定混凝土材料的真实参数,合理评估混凝土结构的真实特性,一直是该领域科研和工程人员矢志不渝的奋斗目标。只有首先得到与尺寸无关的混凝土材料参数,才能正确评价混凝土结构真实性能[1 − 5]。然而,大量试验研究结果表明(徐世烺等[6 − 7],Hillerborg[8],Wittmann[9],钱觉时等[10],杨成球等[11],吴智敏等[12],Zhao等[13],Hoover等[14],胡少伟等[15],Çağlar等[16],Ghasemi等[17],Rong等[18],Yu等[19]):实验室条件下小尺寸试件测得的混凝土材料特性(如断裂与强度参数)存在明显尺寸效应,则试验成果不能直接应用于实际结构。因此,发展由处于准脆性断裂条件下的小尺寸试件确定无尺寸效应的材料真实参数的理论、应用模型与试验方法,建立混凝土结构破坏的个性化预测与设计方程等,是混凝土材料与结构研究领域亟待解决而尚未完全解决的关键科学问题。
尺寸效应理论及其模型建立的重要目的,是寻求小尺寸试件试验结果与真实结构间的转化关系,进而基于该关系,由实验室条件下小尺寸试件的试验结果来评价实际结构的真实性能。目前,国内外混凝土领域应用较多的尺寸效应模型为尺寸效应模型(SEM)[20 − 21]和边界效应模型(BEM)[22 − 24]。几何相似试件(试件高度W变化而缝高比α=a0/W不变,a0为初始裂缝长度)与非几何相似试件(试件α变化而W不变)分别为尺寸效应模型和边界效应模型的推荐试验试件型式。
基于SEM和BEM,可由处于准脆性断裂状态下的混凝土试件的试验数据,通过对其拟合回归分析,确定出无尺寸效应的混凝土断裂韧度KIC与拉伸强度ft[25 − 32]。SEM的理论表达式较为复杂且参数较多,并且对于不同缝高比α的试件,其对应不同的理论公式,不便于工程应用。BEM的应用表达式相对简洁,但对于小尺寸的非几何相似试件,其几何形状参数(等效裂缝长度ae)变化相对较小,造成试验数据的回归效果欠佳。因此,若能基于BEM模型表达式,而采用等效裂缝长度ae变化较大的试件(缝高比α较小的几何相似试件),就可得到较为理想的材料参数确定效果。
由此,本文理论上阐述了采用几何相似和非几何相似试件,确定混凝土材料参数KIC和ft的效果。考虑SEM和BEM的各自优势,基于几何相似、非几何相似、几何与非几何相似等试件的断裂试验研究,通过统计归纳,得出了考虑骨料代表尺寸的混凝土试件峰值荷载Pmax时虚拟裂缝扩展量Δafic的计算方法,进而建立了不同试件型式下的确定混凝土KIC和ft等材料参数的方法。基于确定的材料参数KIC和ft,构造了预测混凝土断裂破坏的设计曲线。进一步,分别建立了Pmax与KIC、Pmax与ft之间的简化解析关系式,从而实现了由Pmax确定KIC、ft的目的。基于该解析公式,对大尺寸实际混凝土结构的峰值极限状态进行了预测。
1 混凝土试件断裂的尺寸与边界效应
1.1 试件尺寸与裂缝长度的相互影响
图1展示带裂缝的试件高度W与裂缝长度a0对断裂特性的影响。
如图1所示,当带裂缝试件的试件尺寸W、初始裂缝长度a0、试件韧带高度W−a0等,都小于一定值(
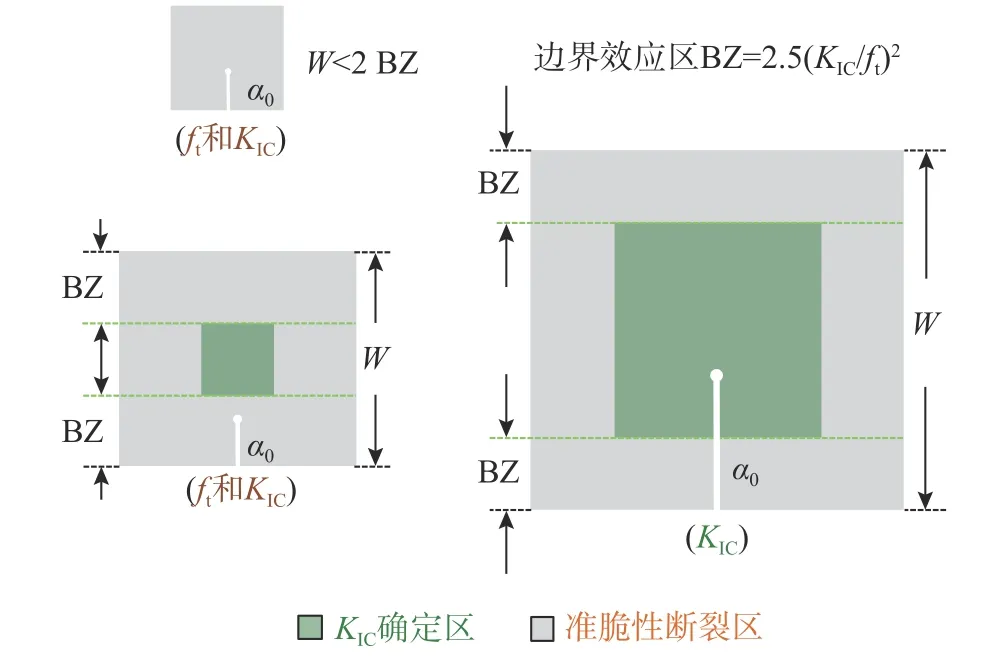
图1 试件尺寸与裂缝长度对断裂特性的影响Fig.1 Effect of specimen size and crack length on fracture characteristics
对于满足线弹性断裂力学条件、可直接应用于实际结构、无尺寸效应的材料参数的获取,其对应的试件尺寸,美国ASTM E399规范[33 − 34]、欧洲BS EN ISO规范[35]等规定,须满足:

式中,B为试件厚度。
基于规范可知,边界效应影响区BZ=2.5(KIC/ft)2。因此,只有尺寸足够大、初始裂缝足够长的试件,才能完全满足线弹性断裂条件,这在普通实验室较难实现。
BEM描述塑性-准脆性-脆性的统一解析表达式为[25 − 32]:



式中:a0为初始裂缝长度;α为试件的缝高比α=a0/W;Y(α)为几何结构参数。对3点弯曲试件,A(α)=(1−α)2;跨高比S/W=8时,
Y(α)=1.106−1.552α+7.71α2−13.53α3+14.23α4,
S/W=4时,

S/W=2.5时,


图2展示试件高度W与裂缝长度a0对几何结构参数ae的影响。对于分析所用试件,ae变化越大,其回归效果越好。
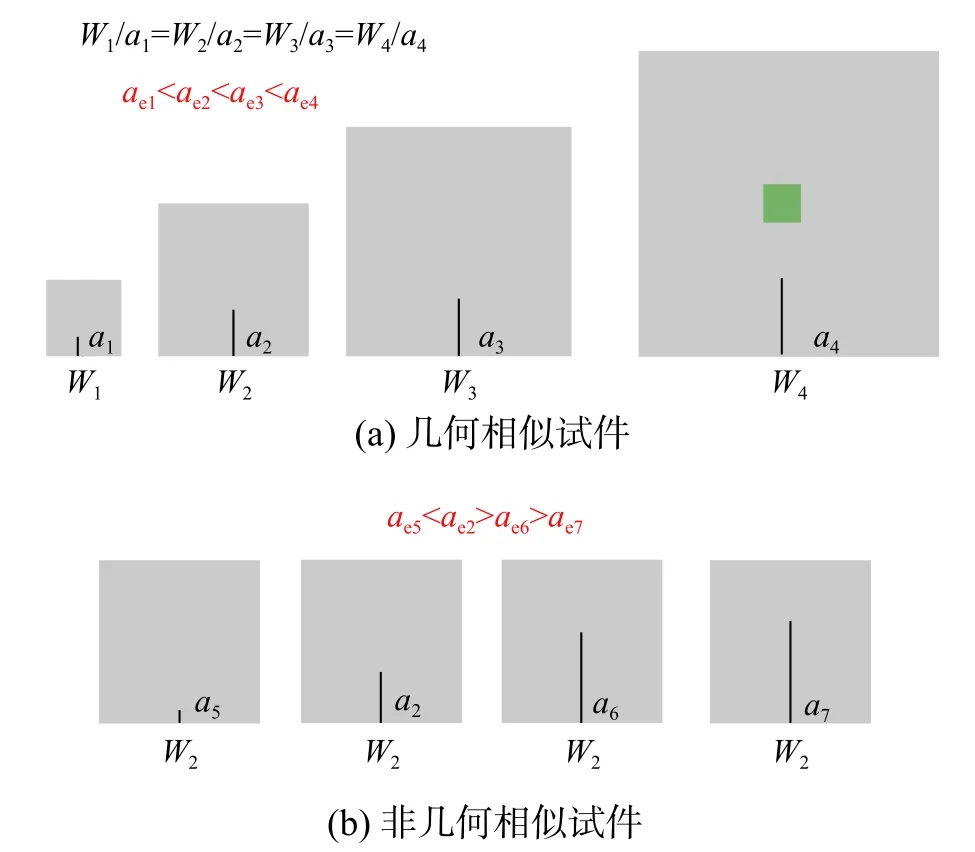
图2 试件高度W与裂缝长度对几何结构参数ae的影响Fig.2 Variation of ae with W and α for geometrically and non-geometrically similar specimens
如图2(a)所示,对于几何相似试件,缝高比α相同而试件尺寸W不同,即a1/W1=a2/W2=a3/W3=a4/W4=α,对应的ae1
图3进一步基于BEM展示了几何相似与非几何相似试件的几何结构参数ae随试件高度W与缝高比α变化而变化的规律。
由图3可见:1)对于几何相似试件:几何结构参数ae的变化范围随着缝高比α=0.2、0.3、0.4、0.1、0.5、0.6、0.7逐渐减小。缝高比α=0.2、0.3对应的ae数值相对较大。2)对于非几何相似试件:当缝高比α=0.2时,几何结构参数ae最大。试件高度W较小时(W1=50 mm和W2=100 mm),ae随着缝高比α变化而变化的范围较小;只有试件高度较大时(W5=300 mm和W6=400 mm),非几何相似试件的ae对应范围变化较大。3)相比较,其他条件相同时,缝高比α=0.2、0.3的几何相似试件所对应的ae变化范围(W1~W4或W2~W6)要大于采用最大试件尺寸(W4或W6)的非几何相似试件时所对应的ae变化范围。

图3 几何相似与非几何相似试件的几何结构参数ae随试件高度W与缝高比α变化的变化规律Fig.3 Variation of ae with W and α for geometrically and non-geometrically similar specimens
当ae变化范围基本一致时,非几何相似试件所需大尺寸试件(W5=300 mm和W6=400 mm;α=0.1、0.2、0.3、0.4、0.5、0.6、0.7)数量要多于几何相似试件(W1~W4或W2~W6)。
由此,确定混凝土断裂与强度参数的最佳试件尺寸设计方案为:采用SEM的几何相似试件型式,试件缝高比α=0.2~0.3。而计算材料参数时,采用BEM相对简洁且考虑了试件尺寸与裂缝长度的相互影响的计算公式。
1.2 试件尺寸、裂缝长度、骨料颗粒的相互影响
BEM表达式在具体应用时,可以变换成回归分析型式:

由试验测试得到各混凝土试件的Pmax,计算出对应的σn(Pmax),由式(3)确定ae,基于式(4),通过数据拟合,即可由外推法同时确定出混凝土的材料参数——断裂韧度KIC和拉伸强度ft。
实验室条件下混凝土试件的W与骨料最大粒径dmax的比值W/dmax为5~20,试件的非均质明显。如图4所示,即使对相同尺寸试件(W和a0不变),其细观层面上的裂缝扩展、试件前后边界、骨料颗粒大小等互相影响,使得有限尺寸试件在宏观上表现出不同的结构特性。
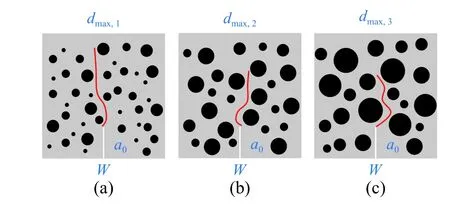
图4 试件尺寸、裂缝长度、骨料颗粒的相互影响Fig.4 Interaction of specimen size, crack length, and aggregate
基于边界效应基本理论,考虑了骨料颗粒、试件前后边界等对断裂破坏的重要影响,课题组提出了离散颗粒断裂模型[30 − 31],基于小尺寸混凝土试件,来确定混凝土的KIC和ft。鉴于骨料颗粒为混凝土材料非均质性的代表体,裂缝扩展时主要围绕骨料颗粒进行(绕骨料或穿越骨料)。因此,改进的离散颗粒断裂模型考虑了峰值荷载Pmax时的虚拟裂缝扩展量Δafic对断裂的影响,并将其与骨料颗粒di相联系,即:

这里,di代表起控制作用的骨料颗粒大小,定义为骨料代表尺寸。基于实际的粗骨料不同粒径分布、筛分曲线、试验筛孔等,可取为di=dmax、dav1、dav2、dmin等。dmax为粗骨料的骨料最大粒径,dmin为粗骨料的骨料最小粒径,dav1和dav2为dmax和dmin间的粒径大小,其具体数值的选取依赖于试验筛分曲线,其可视为不同骨料的平均粒径。
图5为基于改进的离散颗粒断裂模型,来描述实验室条件下有限尺寸混凝土试件裂缝跨越骨料颗粒扩展的物理机理。图5(a)为有限尺寸混凝土试件的骨料分布示意。为便于分析机理,图5(a)可简化为图5(b)的骨料均匀分布形式。

图5 有限尺寸试件的离散颗粒断裂模型Fig.5 Discrete particle fracture model for limited size of concrete specimens
图5展示了有限尺寸混凝土试件的骨料颗粒离散分布的特性:裂缝扩展受控于试件前边界,则Pmax时的Δafic受限。裂缝扩展是跳跃和不连续地,当相对尺寸(W−a0)/di≈10时,仅扩展一个骨料颗粒di,如图5(b)所示。本文通过统计分析,证明了该结论的适用性与可行性。
对于峰值荷载时名义应力的计算,SEM采用σN;BEM采用考虑初始裂缝影响和虚拟裂缝扩展量Δafic影响的σn,两者应力分布的比较见图6。

图6 SEM中σN与BEM中σn的比较Fig.6 Comparison between σN of SEM and σn of BEM
如图6所示,SEM的σN未考虑初始裂缝a0影响,σN不能描述虚拟裂缝扩展和骨料颗粒的影响;而BEM的σn,可考虑Δafic和di两者的影响。对于研究带缝混凝土试件的断裂特性,SEM的σN缺乏明晰的物理意义。基于图6的应力分布,可建立相应的平衡方程,得出σn在Pmax时的解析表达式[25 − 31, 36]:

式中,S为试件有效跨度。
2 基于几何与非几何相似试件确定混凝土的断裂韧度与拉伸强度
分别采用骨料最大粒径dmax=19 mm和dmax=25 mm的两组混凝土断裂试验为分析对象。每组配合比对应设计几何相似与非几何相似两种类型试件。试件为三点弯曲型式,试件尺寸及实测Pmax见表1和表2,其他信息可见文献[37]。

表1 dmax=19 mm混凝土试件尺寸与实测PmaxTable 1 Detailed dimensions of concrete specimens with dmax=19 mm and experimental Pmax

表2 dmax=25 mm混凝土试件尺寸与实测PmaxTable 2 Detailed dimensions of concrete specimens with dmax=25 mm and experimental Pmax
对于dmax=19 mm的混凝土,其粗骨料连续级配为4.75 mm~9.5 mm~12.5 mm~19 mm[37]。则基于离散颗粒断裂模型,可选定dmax=19 mm,dav1=12.5 mm,dav2=9.5 mm,dmin=4.75 mm。相应地,对于dmax=25 mm的混凝土,其粗骨料连续级配为4.75 mm~9.5 mm~12.5 mm~19 mm~25 mm[37]。则可确定dmax=25 mm,dav1=19 mm,dav2=12.5 mm,dav3=9.5 mm,dmin=4.75 mm。

2.1 由几何相似试件确定dmax=19 mm的混凝土的断裂韧度KIC与拉伸强度ft
dmax=19 mm的几何相似试件的高度W=57 mm、114 mm、228 mm、456 mm,缝高比α=a0/W=0.3。通过前文分析可知,α=0.3时几何相似试件的ae变化相对较大,且该组试件的最大与最小试件相似比达到1∶8,其回归效果相对较好。
基于本文所提模型与方法,采用dmax=19 mm的几何相似试件,在不同情况下确定混凝土的断裂韧度KIC与拉伸强度ft如图7所示。
由图7可见,对于小尺寸试件(如W=57 mm),其韧带高度W−a0与dmax的比值相对较小(如W=57 mm, (W−a0)/dmax=2.1),因此,Pmax时的裂缝扩展必定受限,其扩展量由dav1、dav2或dmin控制(如W=57 mm, (W−a0)/dmin=8.4),而不由dmax控制。而对于较大尺寸试件(如W=456 mm),其相对尺寸(W−a0)/dmax相对较大,则裂缝可连续扩展1~2个dmax(如W=456 mm, (W−a0)/(2dmax)=8.4)。
由图7可见,Δafic=0,即忽略峰值荷载时的虚拟裂缝扩展量,造成确定的ft偏大(图7(a))。基于本文模型,除Δafic=dav1、dmax外,其他Δafic≠0情况确定的KIC=1.14 MPa·m1/2~1.63 MPa·m1/2,与SEM确定值KIC=1.39 MPa·m1/2基本吻合;其他Δafic≠0情况确定的ft=5.95 MPa~6.92 MPa,与试验值fts=6.7 MPa基本吻合。
而对于不同高度的试件,Δafic统一取单个骨料大小时(图7(b)~图7(e)),特别是Δafic=dmax时,数据拟合的相关系数R2较小(图7(e),R2=0.3412)。而当Δafic随高度变化个性化取值时,特别是对应的(W−a0)/di≈10时,试验数据回归分析时的相关系数R2达到最大值(图7(i),R2=0.9331)。

图7 由几何相似试件确定dmax=19 mm混凝土的KIC与ftFig.7 Determination of KIC and ft using geometrically similar concrete specimens with dmax=19 mm
2.2 由非几何相似试件确定dmax=19 mm的混凝土的断裂韧度KIC与拉伸强度ft
dmax=19 mm的非几何相似试件的α=0.1、0.2、0.4、0.6。对于大缝高比试件(如α=0.6),其W−a0与dmax的比值相对较小(如α=0.6, (W−a0)/dmax=3),因此,Pmax时Δafic由dav1、dav2或dmin控制(如α=0.6, (W−a0)/dmin=12),而不由dmax控制。
基于本文所提模型与方法,采用dmax=19 mm的非几何相似试件,在不同情况下确定混凝土的KIC与ft如图8所示。
对于不同缝高比的试件,Δafic统一取单个骨料大小时(图8(c)、图8(d)、图8(e),Δafic=dav2、dav1、dmax),数据拟合不能得出相应结果,或相关系数R2较小(图8(b),Δafic=dmin,R2=0.4401)。而个性化Δafic≠0情况下,确定的KIC=0.93 MPa·m1/2~1.05 MPa·m1/2,略小于SEM确定值KIC=1.39 MPa·m1/2(SEM未考虑Δafic);确定的ft=5.43 MPa~5.99 MPa,略小于试验值fts=6.7 MPa(一般情况下fts大于ft)。这与所用非几何相似的ae变化范围相对较小有关。各种情况下,当对应的(W−a0)/di≈10左右时,R2达到最大值(图8(i),R2=0.9235)。
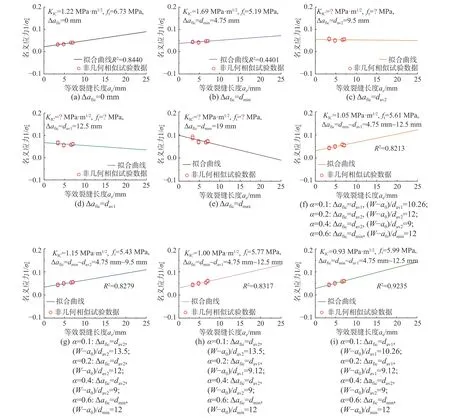
图8 由非几何相似试件确定dmax=19 mm的混凝土的断裂韧度KIC与拉伸强度ftFig.8 Determination of KIC and ft using non-geometrically similar concrete specimens with dmax=19 mm
2.3 由几何与非几何相似试件确定dmax=19 mm的混凝土的断裂韧度KIC与拉伸强度ft
采用dmax=19 mm的几何相似及非几何相似试件,基于本文所提模型与方法,在不同情况下确定的混凝土的KIC与ft如图9所示。
由图9可见,采用几何与非几何相似试件整体分析,个性化Δafic≠0情况确定的KIC=1.24 MPa·m1/2~1.53 MPa·m1/2,ft=5.19 MPa~5.68 MPa,与基于本文模型,分别采用几何相似和非几何相似试件确定的材料参数值基本一致。同样,Δafic统一取单个骨料大小时,数据拟合相关系数R2相对较小。而当Δafic个性化取值,即对应的(W−a0)/di≈10时,R2达到最大值(图9(i),R2=0.8323)。

图9 由几何相似与非几何相似试件确定dmax=19 mm的混凝土的断裂韧度KIC与拉伸强度ftFig.9 Determination of KIC and ft using geometrically similar and non-geometrically similar concrete specimens with dmax=19 mm
2.4 由几何相似试件确定dmax=25 mm的混凝土的断裂韧度KIC与拉伸强度ft
dmax=25 mm的几何相似试件的高度W=75 mm、150 mm、300 mm,缝高比α=a0/W=0.3。
基于本文所提模型与方法,采用dmax=25 mm的几何相似试件,在不同情况下确定的混凝土的KIC与ft如图10所示。
由图10可见,对不同试件高度,Δafic统一取单个骨料大小时,数据拟合不能得出相应结果(Δafic=dav1、dmax),或相关系数R2较小(dmin、dav3、dav2)。基于本文模型,除Δafic=dav3、dav2外,其他Δafic≠0情 况 确 定 的KIC=1.10 MPa·m1/2~1.58 MPa·m1/2,与SEM情况确定值KIC=1.42 MPa·m1/2基本吻合;其他Δafic≠0情况确定的ft=6.17 MPa~7.11 MPa,与试验值fts=6.6 MPa基本吻合。而(W−a0)/di≈10时,R2达到最大值(图10(i),R2=0.9499)。

图10 由几何相似试件确定dmax=25 mm的混凝土的断裂韧度KIC与拉伸强度ftFig.10 Determination of KIC and ft using geometrically similar concrete specimens with dmax=25 mm
2.5 由非几何相似试件确定dmax=25 mm的混凝土的断裂韧度KIC与拉伸强度ft
dmax=25 mm的非几何相似试件的α=0.1、0.2、0.4、0.6。对于大缝高比试件(如α=0.6),其W−a0与骨料最大粒径dmax的比值相对较小(如α=0.6,(W−a0)/dmax=2.28),因此,Pmax时Δafic由dav1、dav2、dav3或dmin控制(如α=0.6,(W−a0)/dmin=12),而不由dmax控制。
基于本文所提模型方法,采用dmax=25 mm的非几何相似试件,在不同情况下确定的混凝土的断裂韧度KIC与拉伸强度ft如图11所示。
由图11可见,对缝高比不同的非几何相似试件,Δafic统一取单个骨料大小,即Δafic=dav3、dav2、dav1、dmax时,回归方法失效(图11(c)、图11(d)、图11(e)、图11(f)),或相关系数R2较小(Δafic=dmin,图11(b))。而个性化Δafic≠0情况确定的KIC=0.91 MPa·m1/2~1.22 MPa·m1/2,略小于SEM确定值KIC=1.42 MPa·m1/2;个 性 化Δafic≠0情 况 确 定 的ft=5.50 MPa~6.31 MPa,略小于实验值fts=6.6 MPa。其与所用试件数量相对较少,ae变化范围相对较小有关。而当对应的(W−a0)/di≈10时,R2达到最大值(图11(i),R2=0.7609)。

图11 由非几何相似试件确定dmax=25 mm的混凝土的断裂韧度KIC与拉伸强度ftFig.11 Determination of KIC and ft using non-geometrically similar concrete specimens with dmax=25 mm
2.6 由几何与非几何相似试件确定dmax=25 mm的混凝土的断裂韧度KIC与拉伸强度ft
基于本文所提模型与方法,采用dmax=25 mm的几何相似及非几何相似试件,在不同情况下确定的混凝土的KIC与ft如图12所示。
由图12可见,Δafic=dmax,回归方法失效(图12(e)、图12(f))或R2相对较小(图12(c)、图12(d))。而个性化Δafic≠0情况下,基于本文模型确定的KIC=1.22 MPa·m1/2~1.38 MPa·m1/2,与SEM确定值KIC=1.42 MPa·m1/2基 本 一 致;确 定 的ft=5.43 MPa~5.70 MPa,略小于试验值fts=6.6 MPa。而(W−a0)/di≈10时,R2达到最大值(图12(j),R2=0.7636)。

图12 由几何相似与非几何相似试件确定dmax=25 mm的混凝土的断裂韧度KIC与拉伸强度ftFig.12 Determination of KIC and ft using geometrically similar and non-geometrically similar concrete specimens with dmax=25 mm
3 基于几何与非几何相似试件确定混凝土断裂全曲线
由图13和图14可见,本文所用的试件都处于准脆性断裂状态,即使最大尺寸试件也未达到线弹性状态。基于全曲线确定的满足线弹性状态的混凝土试件的理论最小尺寸W超过1200 mm。

图13 构建dmax=19 mm混凝土的断裂破坏曲线Fig.13 Fracture curves of concrete with dmax=19 mm
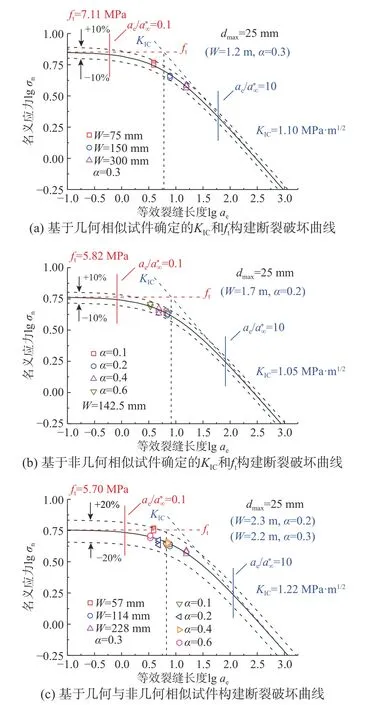
图14 构建dmax=25 mm混凝土的断裂破坏曲线Fig.14 Fracture curves of concrete with dmax=25 mm
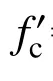

图15 构建dmax=19 mm和dmax=25 mm混凝土的断裂破坏曲线Fig.15 Fracture curves of concrete with dmax=19 mm and dmax=25 mm
4 基于简化解析公式预测混凝土峰值荷载和断裂韧度及拉伸强度
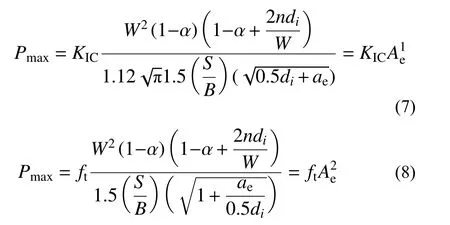
式中,根据本文方法,当(W−a0)/di≈10,n=1;(W−a0)/di≈20,n=2。
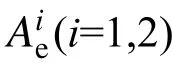
基于简化解析表达式(7)和式(8),确定的KIC或ft,与本文模型式(2)~式(6)确定的KIC与ft理论值的比较结果可见图16~图18。
由图16~图18可见,简化解析公式确定的KIC与ft,与理论确定值基本一致。除dmax=25 mm的几何相似试件外(试验数据偏少),其他情况下的预测直线的相关系数R2≥0.96。基于简化解析公式确定的预测值的±15%可涵盖所有试验数据。


图16 基于几何与非几何相似试件对dmax=19 mm混凝土的Pmax、KIC、ft进行预测Fig.16 Predicting Pmax, KIC and ft of concrete with dmax=19 mm using geometrically and non-geometrically similar specimens


图17 基于几何与非几何相似试件对dmax=25 mm混凝土的Pmax、KIC、ft进行预测Fig.17 Predicting Pmax, KIC and ft of concrete with dmax=25 mm using geometrically and non-geometrically similar specimens

图18 基于dmax=19 mm和dmax=25 mm的几何与非几何相似试件对混凝土的Pmax、KIC、ft进行预测Fig.18 Predicting Pmax, KIC and ft of concrete with dmax=19 mm and 25 mm using geometrically and non-geometrically similar specimens
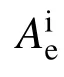
5 结论
本文结合BEM和SEM模型的优点,推荐了确定混凝土断裂与强度参数的最佳试件尺寸设计方案;研究了由几何相似与非几何相似试件确定混凝土断裂韧度与拉伸强度的模型及其应用方法。通过不同骨料颗粒大小的几何相似、非几何相似、几何相似与非几何相似等不同类型的混凝土断裂试验的详细分析,验证了所提模型与方法的合理性与适用性。研究得到如下结论:
(1) 对于几何相似试件,其他条件相同时,缝高比α=0.2、0.3对应的几何结构参数ae的数值相对较大。对于非几何相似试件,当缝高比α=0.2时,几何结构参数ae最大;试件高度W较小时,ae随着缝高比α变化的范围较小。其他条件相同时,缝高比α=0.2、0.3的几何相似试件对应的ae的变化范围大于非几何相似试件。则确定混凝土断裂与强度参数的试验设计,推荐采用SEM的几何相似试件型式,α=0.2~0.3;计算材料参数时,选用BEM的计算公式。
(2) 发展了离散颗粒断裂模型。考虑混凝土粗骨料级配的影响,给出了有限尺寸试件峰值荷载Pmax时的虚拟裂缝扩展量Δafic简化计算方法。通过本文详细分析,有限尺寸混凝土试件Pmax时的Δafic受限,当(W−a0)/di≈10时,Δafic可取di。本文模型确定的材料参数值与试验测试强度值,以及尺寸效应模型确定的断裂韧度值吻合良好。当(W−a0)/di≈10,取Δafic=di,对应的试验数据回归的相关系数最佳。而Δafic统一取单个骨料大小时,特别是Δafic=dmax时,数据拟合的相关系数较小或回归方法失效。
(3) 基于几何相似、非几何相似、几何相似与非几何相似试件确定的断裂韧度与拉伸强度,可分别建立起描述混凝土材料的强度—准脆性断裂—断裂韧度控制的断裂破坏全曲线。建立曲线的±20%可涵盖全部试验数据。本文实验室层面的试验数据基本在准脆性断裂控制区域。
(4) 建立了峰值荷载与断裂韧度、峰值荷载与拉伸强度之间的简化解析表达式。等效面积与实测峰值荷载展现出良好相关性;由两点直线法直接确定出的断裂韧度与拉伸强度值,与理论模型确定值基本一致。预测值的±15%可涵盖所有试验数据。基于简化解析公式,预测了满足线弹性断裂力学对应的大尺寸试件的峰值荷载。
