基于EM算法和模态形式的状态空间模型自降阶工作模态分析
2021-09-23施袁锋朱正言戴靠山
施袁锋,朱正言,陈 鹏,戴靠山
(1. 四川大学建筑与环境学院深地科学与工程教育部重点实验室,四川,成都 610065;2. 四川大学破坏力学与工程防灾减灾四川省重点实验室,四川,成都 610065;3. 浙江大学建筑工程学院,浙江,杭州 310058)
模态分析是近年结构健康监测领域的热点之一[1 − 2],其获取的结构模态参数在既有结构的动力特性评价、结构损伤诊断、结构振动控制等领域具有重要应用。工作模态分析只需测量结构在环境激励下的响应信号便可进行模态参数识别,具有操作简单可行、试验经济等特点,因而在工程领域中得到了广泛应用[3 − 5]。近年来,很多学者分别在时域内和频域内提出了各种工作模态分析方法[3 − 7]。
对于时域内的模态分析方法如自回归移动平均时序法(ARMA)、随机子空间识别法(SSI)、特征系统实现算法(ERA),模型阶次的选择或确定直接影响着模态参数识别的维度、准确性和稳定性[8]。环境激励下的结构实测振动响应,因环境非平稳激励、结构非线性行为、测量噪声和建模误差的影响,给模态分析中模型阶次的确定带来了实际困难。目前,基于状态空间模型的模型阶次的确定通常利用Hankel矩阵的奇异值分解并结合稳定图的方法[9]。由于稳定图法不能完全排除非平稳激励、噪声等干扰的影响,学者们提出了一些解决这一影响的改进方法。常军等[10]提出了两阶段稳定图的随机子空间结构模态参数识别方法。易伟建和刘翔[11]提出了以奇异值分解后的残差期望为依据的模型定阶方法。王树青等[12]从奇异值相对变化率、崔伟成等[13]从拟合误差最小化原则、朱锐等[14]从奇异值百分比变化增量、廖聿宸等[15]从基于奇异值的函数拟合分别提出了相应的模型定阶方法。由于建立Hankel矩阵本身的影响,上述基于奇异值分解和稳定图的模型定阶方法还是存在较大主观性。Cara等[16]于是从一个新的角度出发,首先建立了一种模态形式的状态空间模型,并提出以模态贡献为指标的状态空间模型阶次选择方法,以仿真和实际结构进行了验证。由于该方法直接以对角化系统状态矩阵出发,整个模态形式的状态方程的模型参数和状态变量为复数型,在一定程度上给后续计算带来不便。
随机子空间识别法在工作模态分析中已有广泛应用[3],但在受系统初值影响的振动响应以及环境激励与测量噪声相关的情况下存在一定的缺陷。针对此,有学者提出了考虑初值影响和考虑环境激励和测量噪声相关的建模,并采用期望最大(EM)迭代算法实现极大似然估计的方法[17 − 19]。EM算法[20]原理简单,不必对目标函数进行复杂微分计算,可直接通过迭代渐近得到极大似然值,因而在基于状态空间模型的系统识别中也得到了实际应用。Cara等[17]、Matarazzo和Pakzad[18]使用随机状态空间建模并以EM算法进行模态参数的估计,但都忽略了实际环境激励与测量噪声的相关性影响。利用Gibson和Ninness[21]建立的系统噪声和观测噪声间相关的状态空间模型EM解法,张康和施袁锋[19]考虑了完整的状态空间参数化建模,获得了更准确的识别结果。张静等[22]应用EM算法实现对状态空间模型的辨识,并利用AIC准则确定状态空间阶次,通过数值分析验证了该方法的有效性。对于维度高的动力系统,EM算法也存在着如收敛速度较慢的问题,因此合理的模型降阶将有助于EM的计算效率。
本文从上述基于状态空间模型的工作模态分析中的不足出发,通过建立一种特殊的模态形式状态空间模型,提出了一种结合EM算法和模态贡献的自降阶工作模态分析方法。该特殊的模态形式状态空间模型的特点是所有的模型参数和状态变量都为实数。通过将EM迭代过程中估计的模型参数转换成模态形式后,引入表征各模态对于总响应的重要性的模态贡献指标,并设定模态贡献阈值来实现对状态空间模型的自动降阶。同时结合频谱分析和阻尼比阈值剔除识别结果的虚假模态。最后通过数值模拟和实测数据分析以验证方法的适用性和有效性。
1 动力系统建模
1.1 状态空间模型
记结构在环境激励下的动力响应观测数据为Y,具体可表示成:

式中:yk∈Rp×1表示系统p个测量通道在k离散时刻的响应向量;Yl∈R1×N为第l个通道的数据总时长为N的响应向量。观测响应数据yk可通过随机状态空间模型来模拟:
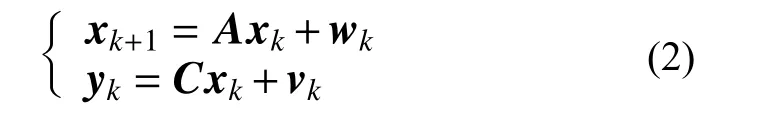
式中:xk∈Rn×1为系统状态向量;n为状态向量的维度,也即模型阶次;A∈Rn×n为系统的状态转换矩阵;C∈Rp×n为系统的输出矩阵,描述内部状态如何转换成输出yk;wk∈Rn×1为系统噪声;vk∈Rp×1为观测噪声。假设系统噪声和观测噪声是具有相关性的高斯白噪声,其联合概率分布为:
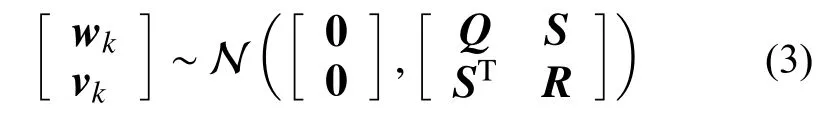
式中:~表示概率分布服从; N(α,β)为高斯概率分布函数, α 为均值,β 为协方差;矩阵Q为系统噪声wk自身的协方差;矩阵R为观测噪声vk自身的协方差;矩阵S为系统噪声和观测噪声两者的协方差。假定系统初始状态x1也满足高斯分布:
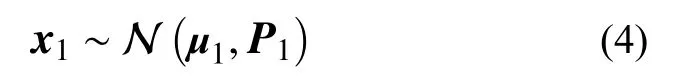
式 中:μ1∈Rn×1为 系 统 初 始 状 态x1的 均 值;P1∈Rn×n为x1的协方差。状态空间模型式(2)的参数化形式可表示成:

式中:θ表示模型所有自由参数组成的向量; ≜为定义符号,表示由右侧各项矩阵中自由参数组成。
式(2)为一般形式的随机状态空间模型,其固有模态频率和阻尼比与矩阵A的复数特征值有关,即:

直接基于式(2)的工作模态分析为通过实测响应Y,采用合理参数估计方法确定模型阶次n和θ的值,进而求解系统相应的模态参数。从实测数据建立动力系统模型的关键步骤之一是确定合理的模型阶次,这对模型估计的准确性和可靠性,以 及计算效率都具有重要意义。
1.2 模态形式状态空间模型
一般形式的状态空间模型,通过相似变换,系统仍具有相同的模态信息和输出性质。先介绍通过相似变换得到一种特殊的模态形式状态空间模型,这种模态形式将用于模型降阶的过程中。
引入一可逆模态形式变换矩阵T,将状态向量xk变成:

代入式(2),可得一特殊模态形式的状态空间方程:
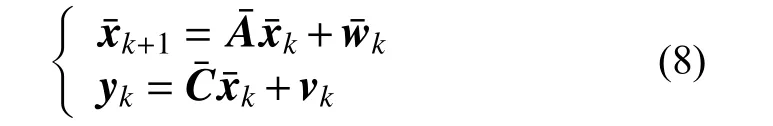


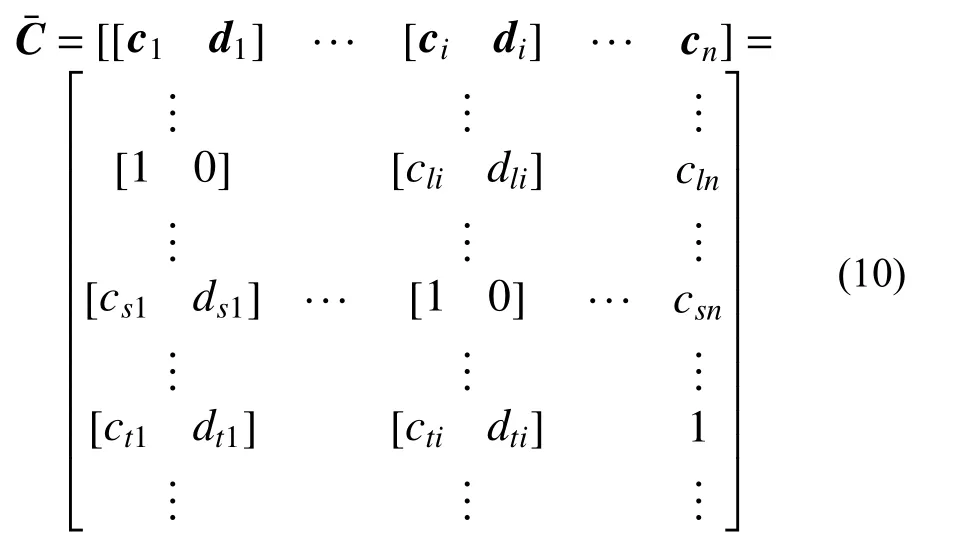

此时,模态形式的状态空间模型(8)的参数化形式可写成:
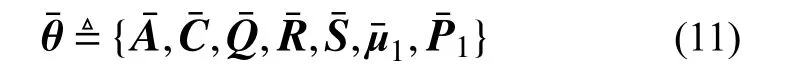
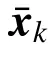
1.3 模态贡献
假设模型参数已知,利用观测数据Y,用卡尔曼滤波可以估计系统状态和输出。当使用模态形式的状态空间模型式(8)时,其卡尔曼滤波为:


因此,利用卡尔曼滤波后,观测数据Y可表示为:

式中:
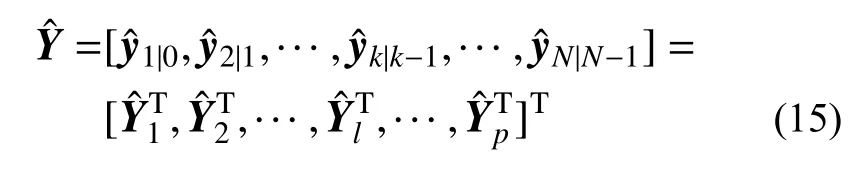




模态贡献指标的大小反映了相应系统特征值的重要性。如果ci越小,说明该模态越有可能是虚假模态,故由此可判断系统模型阶次可能过高。相关学者在研究模态贡献时,将各阶模态在所有输出通道上的贡献进行平均处理,以此定义模态的全局贡献[16]。但在分析中发现,经过平均处理会削弱真实模态的贡献,本文为了避免某些贡献较小的真实模态因平均处理被剔除,定义模态贡献为每个模态在各输出通道中的最大贡献值,用以代替平均值表征模态重要性,从而提高对真实模态的识别能力。
2 基于EM算法和模态形式的状态空间模型自降阶方法
由于极大似然估计方法具有渐近无偏估计、渐近一致性和渐近有效性等优异特性,本文采用极大似然法来实现随机状态空间模型参数 θ的估计,进而获取结构的工作模态参数。然而模型参数的极大似然值的求解是一复杂的非线性优化问题,直接求解往往具有较大困难,特别是对于高维参数估计问题。EM迭代算法的提出,提高了一些问题的极大似然估计的实际应用性,其中包括状态空间模型的参数估计问题[22]。前文已指出模型阶次确定的重要性,结合模态形式状态空间模型,在这里描述本文基于EM算法的模型降阶识别的方法。
2.1 EM算法


式中:似然函数L(θ|Y)=lnp(Y|θ) ,其中p(Y|θ)是测量数据Y在模型 θ下的概率密度函数。引入X为未观测值,令系统完整数据Z=(X,Y)。由贝叶斯公式可得:

式(20)两边同时取对数,有:
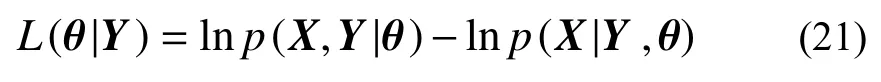



2.2 模型阶次确定
由1.3节得到,模态响应直接反映了系统的固有特性和激励对系统输出的影响,而模态贡献反映了各个模态的重要性。因此提出在EM迭代过程中在满足数据拟合条件下,剔除模态贡献小的模型参数进行模型的降阶。显然,更高阶数的状态空间模型包含更多的模态信息,可以更好地拟合响应数据,但也带来了过于拟合的情况,由此获得的模态信息中必然包括结构的真实模态和相当数量的可忽略的虚假模态,同时会增加计算时间。为筛选出真实可靠的模态信息,需要把其中模态贡献指标较小的模态剔除,引入一个贡献阈值 [c]用于删除那部分贡献很小的模态,实现模型的降阶。
关于EM何时执行降阶和收敛,以似然函数值相对变化率建立相关的判别式 ρ作为判据指标,并确定参数 ρ0作为降阶的判断阈值和 ρg作为全局收敛的阈值:

由于式(25)~式(33)为全参数模态形式EM迭代结果,因此在EM迭代过程中满足降阶条件时,需将模型参数转换到模态形式后计算各模态贡献,当模态贡献中的最小值小于设定的阈值[c]并且拟合残差满足白噪声要求时,便删除与之对应的模态信息,实现降阶。当最小贡献对应的模态为复模态,需要去除参数矩阵中对应的2次模型阶次;当最小贡献的模态对应为实模态,则去 除参数矩阵中对应的1次模型阶次。
2.3 模型估计和自降阶过程
基于EM算法和模态形式的状态空间模型自降阶工作模态分析的过程见图1,具体执行步骤为:
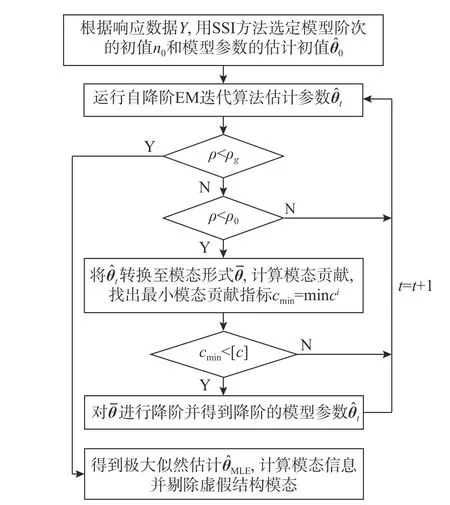
图1 自降阶工作模态分析流程图Fig.1 Flowchart of operational modal analysis with auto model order reduction
1) 根据观测响应数据Y,使用随机子空间方法(SSI)确定一个相对较大的模型阶次初值n0和模型参数的估计初值 θ0。
4) 当最小模态贡献指标超过贡献阈值 [c]时,此时得到算法建议的最终模型阶数n,EM算法迭代继续至满足EM全局收敛条件 ρg时停止。
此外,执行降阶EM算法需要设定几个参数,这里介绍相关参数的设置原则:
1) 状态空间模型阶次初值n0:为了使更多的真实模态信息被包含,同时状态空间阶次又不过分大,检验用SSI方法确定模型阶次和估计参数初值后得到响应估计残差ε ,当残差 ε的频谱图中无明显孤立峰值时可认为识别系统在整体上符合白噪声假设条件。此时可认为选取的模型阶次初值n0大小是合适的,否则,增大模型阶次初值。
2) 模态贡献阈值 [c]:使用SSI方法试算得到模态信息,然后计算出模态响应和各模态的模态贡献;结合频谱图初步确定结构模态,特别是具有独立峰值但峰值低而窄的可能结构模态,在结构模态贡献中找到最小的模态贡献;确定比最小结构模态贡献稍小的值作为模态贡献阈值,建议以1‰为基数。
3) 降阶条件 ρ0:通常EM算法收敛阈值 ρ0小于 10−5即可,所以每次降阶前确保EM达到一定程度收敛,这可根据模型阶次的大小进行相应调整,状态空间阶数较小时 ρ0可以更小一点,状态空间阶数较大时 ρ0可适当放宽。
4) 全局收敛标准 ρg: ρg为不能降阶时EM算法的最终迭代收敛标准,其可在 ρ0的基础上进行适当降低,一般降低一个数量级即可。
5) 虚假结构模态剔除:除了在模型降阶过程中模态贡献小的虚假模态之外,最终模型的模态信息中还会存在一些非结构模态的虚假模态。为了对这些非结构的虚假模态加以判别,还需结合输出响应的频谱分析,相互佐证以提高识别结果的可信度。同时将模态的阻尼比信息考虑进来,一般而言,环境激励下的建筑结构的阻尼比通常小于5%,并且考虑到以往的研究提到阻尼比的识别没有特别可靠的方法,所以针对结构阻尼比判定可以适当放宽[23]。基于此,设定结构阻尼比阈值为 ζc=10%,当识别模型某个模态的阻尼比超过该阈值便视为虚假模态并予以剔除。也可以通过分析模态参数的不确定性水平[5],把不确定性水平大的模态认定为虚假模态予以剔除。
3 应用举例
下面以数值模拟和现场实测的结构振动响应分析来对本文提出的方法进行验证说明。
3.1 6自由度结构数值模拟分析
一个6层剪切型结构简图如图2所示,各质点质量为mi=1t ,i=1,2,···,6;层间刚度分别为k1=1300 ,k2=1200 ,k3=1100 ,k4=1000,k5=900 ,k6=800,单位kN/m。结构的阻尼形式假设为Rayleigh阻尼,其第1阶和第6阶模态对应阻尼比均为5%。所有自由度上施加相同强度的白噪声作为模拟结构的环境激励。采集所有自由度上的加速度响应,采样频率fs=50Hz,时长为100 s。此外在结构的输出响应中加入相同强度的白噪声以模拟传感器采集数据时的观测噪声。

图2 6自由度结构模型简图Fig.2 Schematic diagram of 6-DOF structural model
图3给出了采集加速度响应的奇异值频谱图,通过其峰值基本可以看出结构的前5阶模态位置,但第6阶模态并不明显。基于采集的6层加速度振动响应信号,下面利用本文方法进行工作模态分析。

图3 6自由度加速度响应奇异值频谱图Fig.3 Singular value spectrum of measured accelerations of 6-DOF structure
此6自由度结构对应于状态空间模型的理论阶次为12。因为一般情况下模型阶次事先未知,首先假定一个较高模型阶次初值n0=24,此模型阶次得到的估计残差一定能满足白噪声条件。EM降 阶 算 法 中 设 定 为 ρ0=1×10−6,ρg=1×10−7,[c]=0.05。图4显示了EM降阶识别的过程,图中给出了每一次降阶对应的似然函数值的变化以及根据收敛标准得到的最终模型阶数和总迭代次数。最终的模型阶次确定为n=12,与真实的模型阶次相同。

图4 6自由度结构EM自降阶迭代过程Fig.4 EM iteration process with auto order reduction of 6-DOF structure
最终识别的模态参数识别结果见表1。对于此数值模拟结构,通过本文识别方法确定了最小的模型阶次后,识别出来的模态全部为结构真实模态,无虚假模态的存在。尽管图3中后几阶频率峰值不明显,由表1的结果可以看出本文方法依然获得了非常准确的模态参数识别结果。表1中同时给出了每个模态所对应的模态贡献值,可以看出一阶频率对应的通道最大贡献是所有模态中最小的,只有0.063,表明一阶模态对结构的总响应的贡献不大,为非优势模态,但实际上该模态实际上是结构的真实模态,不应该被剔除,说明合理设置模态贡献阈值是非常关键的一步。通常,我们需要在一定程度上借助频谱图的重要模态确定可行的模态贡献阈值。图5给出了模态振型的识别结果,可见所有振型都吻合得很好。综合表1和图5,带有降阶EM算法对结构响应进行了有效处理,并获得了非常好的结构模态信息。

表1 6自由度模态分析结果Table 1 Modal analysis results of 6-DOF structure

图5 6自由度振型识别结果Fig.5 Identified mode shapes of 6-DOF structure
为演示模态贡献的概念,以下以质点2的振动响应数据为例进行说明。首先,图6(a)展示了质点2处10 s~20 s时间段内的真实和采集的加速度响应的时程曲线。由于模拟测量噪声较大,可见图6(a)中真实加速度序列和测量加速度序列相差较大。使用模态形式状态空间模型求得各阶模态在质点2处的模态响应和模态贡献,通过振型叠加得到质点2的拟合加速度响应。各阶模态响应及贡献如图7所示,可以看出模态1和模态4的振幅都非常小,模态贡献都小于1%,比表1中对应模态的通道最大贡献还小很多;模态2、模态3、模态6的响应幅值较大,对应的模态贡献也比较大,意味着这3个模态于质点2而言是优势模态。

图6 6自由度结构质点2处(10 s~20 s)加速度响应分析Fig.6 Analysis of acceleration response at mass No.2 of 6-DOF structure (10 s-20 s)

图7 6自由度结构质点2处(10 s~20 s)各阶模态响应及贡献Fig.7 Modal response and contribution ratio at mass No.2 of 6-DOF structure (10 s-20 s)
将质点2处各阶模态响应叠加可得到其最终拟合加速度曲线,如图6(b)所示。从图6(b)中看出,得到的拟合加速度曲线在幅值较高的地方与真实加速度有一定误差,这是由于原始信号中包含了很高的噪声成分,从而影响了对结构响应的估计,但与图6(a)相比,拟合的加速度响应与真实响应较接近。
3.2 广州塔实测振动分析
为了验证本文方法对实际结构的模态分析能力,选择广州新电视塔(以下简称“广州塔”)为应用对象。国内外已有许多学者[23 − 26]对广州塔在环境激励下进行了模态分析研究。本节通过对广州塔的环境振动数据进行模态分析,尝试在0 Hz~5 Hz间确定一个合适的状态空间阶次并估计可靠的模态信息。
广州塔传感器布置如图8所示,在8个不同高度总共安装有20个水平加速度传感器,分别沿截面的长轴和短轴方向布置。2010年1月19日—20日,基准测试工作组采集了广州塔在环境激励下24 h的加速度响应数据。这里随机选用1月20日18:00~19:00间的测量数据进行分析(数据来源:http://www.zn903.com/ceyxia/benchmark/index.htm)。原始测量数据的采样频率为50 Hz,因此每个通道的采样点数量N=180000。考虑到主要考虑结构低阶范围内的模态信息,我们对原始信号进行滤波重采样处理,以减少数据量并提高计算效率。对原始测量数据使用巴特沃斯低通滤波,截断频率为5 Hz,然后以10 Hz进行重采样,采样点降为N=36000。

图8 广州塔水平加速度传感器布置简图Fig.8 Layout diagram of horizontal acceleration sensor placement for Canton Tower
图9给出了部分传感器(传感器6、12和16)在18:00~19:00的加速度响应曲线,所有传感器获得的加速度响应的奇异值频谱图如图10所示。可以发现3 Hz~5 Hz结构的模态信息成分非常复杂,不易辨认。

图9 广州塔传感器(6、12和16)加速度响应曲线Fig.9 Acceleration responses from sensors(6, 12 and 16) on Canton Tower
针对重采样的所有数据,应用本文方法展开模态识别。首先,设置初始状态空间阶数n0=160 ,EM算法降阶条件设为ρ0=5×10−6,全局收敛率 ρg=1×10−6,设置模态贡献阈值 [c]=0.005,带有模型降阶识别过程如图11所示,图中每次似然函数值突降点为进行了模型降阶,最后确定的模型阶数为n=119,相比于模型阶次初值有较大减少。由于广州塔结构复杂,存在较多的模态,所以需要较大模型阶次得到合理的识别模型,这一点也可以从图10中预见到。图12展示了最终确定模型阶次后的估计残差奇异值频谱图。尽管图12中也存在一些小峰值,但因为这些峰值对应的模态贡献都非常小,可认为其为噪声,残差频谱图在整体上看可认为符合高斯白噪声分布。综合图11和图12,可以认为模型阶次得到了合理的确定。
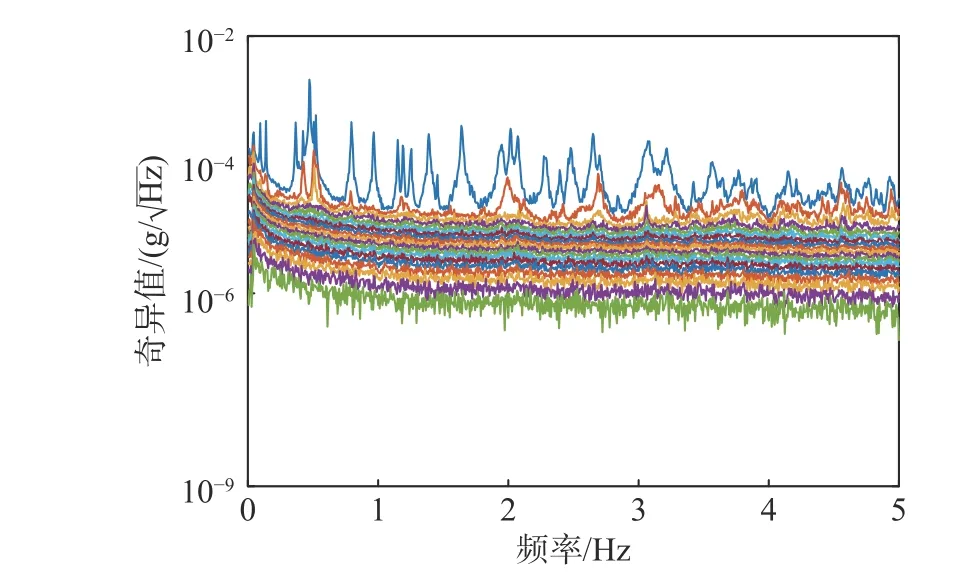
图10 广州塔加速度响应奇异值频谱图Fig.10 Singular value spectrum of acceleration responses of Canton Tower

图11 广州塔EM自降阶迭代过程Fig.11 EM iteration process with auto order reduction of Canton Tower

图12 广州塔识别模型的响应估计残差奇异值频谱图Fig.12 Singular value spectrum of residuals of the identified model for Canton Tower
最终得到的模型所有模态信息包含13个实模态和53个复模态,但由于激励假设误差、建模误差、噪声等影响,这些模态信息既包含结构的真实模态,又包含虚假模态。因此,需要结合结构模态的特征来对识别结果进行筛选处理。利用加速度响应奇异值频谱图及一般结构阻尼判据ζc=10%,对虚假模态进行剔除。将剔除虚假模态后的最终前12阶模态信息与Ye等[23]使用NExTERA方法得到的结果列于表2,可以看出本文方法与NExT-ERA方法对于频率的识别具有很好的一致性,两者得到的模态信息极为接近。此外本算例中使用的数据信息频宽为0 Hz~5 Hz,在这个范围内可以获得更多对结构响应贡献较大的模态,这对广州塔的模型更新具有更多应用价值。
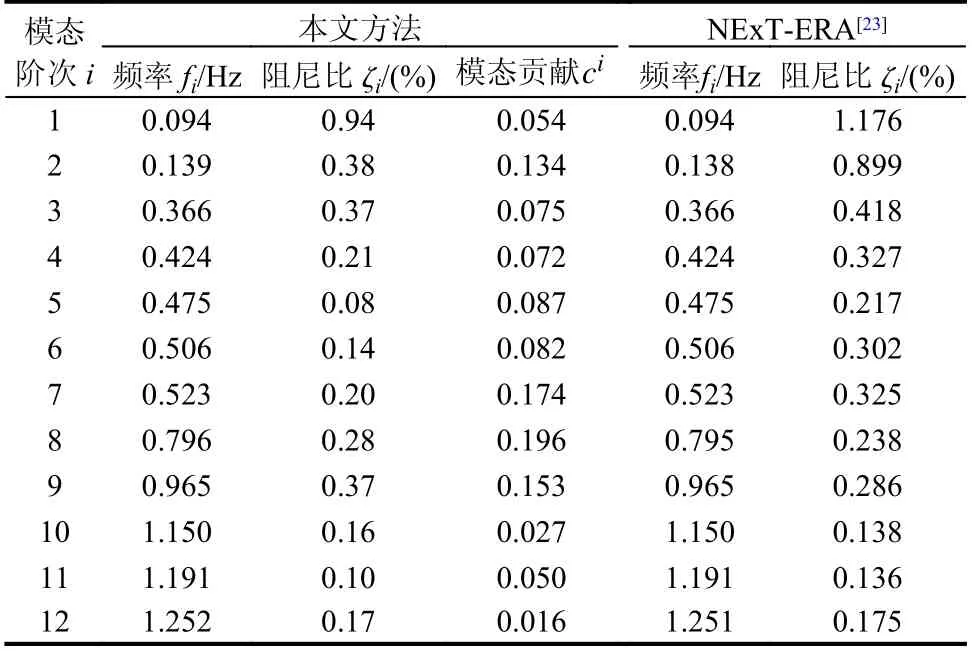
表2 广州塔本文方法与NExT-ERA[23]识别结果比较Table 2 Comparison of the identified results of the proposed method and NExT-ERA[23] for Canton Tower
图13和图14画出了广州塔前12阶模态振型分别在x方向和y方向的分量,可以通过比较判断出模态振型在2个方向上的耦合情况,比如模态1和模态2都在一个特定方向呈现出弯曲型特征,而在另外一个方向的振幅很小,说明模态1和模态2在相互正交的方向上耦合效应不明显,符合结构的一阶振型特征。
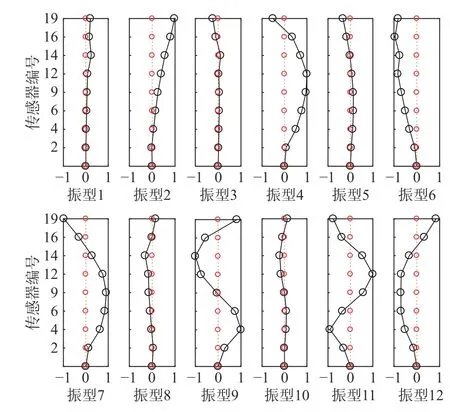
图13 广州塔前12阶振型在x方向的分量(横截面长轴)Fig.13 The x-component of the first 12 identified modes of Canton Tower (the longitudinal axis of the cross section)
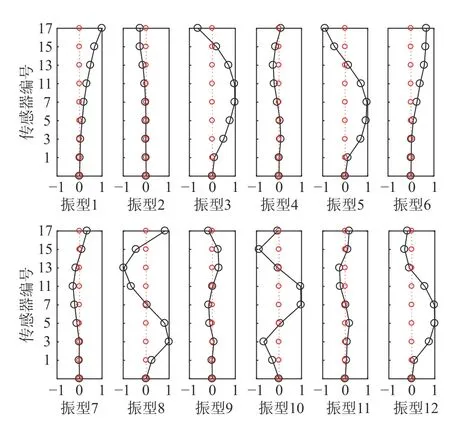
图14 广州塔前12阶振型在y方向的分量(横截面短轴)Fig.14 The y-component of the first 12 identified modes of Canton Tower (the transverse axis of the cross section)
4 结论
本文提出了利用一种特殊的模态形式状态空间模型,在EM迭代算法求解模型参数的极大似然估计中实现模型降阶和模态参数估计的方法。重点可以概况如下:
(1) 基于模态形式状态空间模型,可利用卡尔曼滤波获得各阶模态的模态响应量。
(2) 提出了表征各阶模态对总响应的重要性的模态贡献指标,以此作为模型降阶标准较之振型参与系数等指标更具有物理意义和有效性。
(3) 提出的方法中一些阈值的选择,仍带有一定的经验性,需结合数据和结构特征进行调整。
(4) 该模型降阶方法的结果虽不容易遗漏真实模态,但结构虚假模态不能全部剔除。因此最后仍需要结合结构模态信息的特征对系统模型全部模态结果进一步筛选。
(5) 通过模拟结构数据和广州塔实测数据的分析,表明本文的方法具有良好的准确率和稳健性。
