ZA型蜗杆副建模及动力学传动误差仿真分析
2021-09-23杨宏斌李官运徐爱军
杨宏斌,李官运,李 静,徐爱军
(河南科技大学机电工程学院,河南 洛阳471003)
1 引言
蜗杆副具有传动平稳、振动和噪声小等优点广泛应用于诸多行业。在蜗轮蜗杆的加工制造、仿真分析等方面,采用精准的蜗杆副三维模型显得十分重要。在齿轮传动的设计中,传动误差是重要的设计参考资料,通过动力学仿真软件,可以分析在不同转速、负载情况下的啮合传动误差[1]。
对于蜗杆副的精确建模可以采用多种方法,文献[2]采用绘制齿廓线进行扫描切除,建立蜗杆副的三维模型,通过VB编程实现蜗杆副的参数化建模。文献[3-5]同样采用参数化建模的方法建立蜗杆副模型,在动力学仿真分析方面,分别对输出角速度和啮合力的变化进行分析。文献[6]建立蜗杆副的虚拟样机模型,对存在安装误差条件下的蜗杆副进行传动误差分析。文献[7]探究一种评估齿轮啮合振动和噪声的数值方法,采用齿轮传动误差来进行评价,通过实验验证动力学仿真软件对传动误差分析的正确性。
文中根据成形加工原理和齿轮啮合原理,对蜗杆副的数学模型进行推导,完成对蜗杆副三维模型的建立。在动力学仿真软件RecurDyn中搭建蜗杆副的动力学模型,对蜗杆副在不同工况下的传动误差进行分析研究,为蜗轮蜗杆的设计和性能分析提供参考。
2 建立ZA型蜗杆副的数学模型
2.1 ZA蜗杆的数学模型
蜗杆的数学模型是根据加工原理,利用加工车刀的直线刃方程,绕着蜗杆轴线做螺旋线运动推导而来[8]。车刀加工蜗杆的螺旋运动情况如图1所示,S1为蜗杆刚性固接的坐标系,Su为车刀固接的动态坐标系,θ为车刀螺旋运动的回转角。

图1 蜗杆加工的坐标系Fig.1 Coordinate System for Worm Machining
右旋蜗杆的数学方程为:
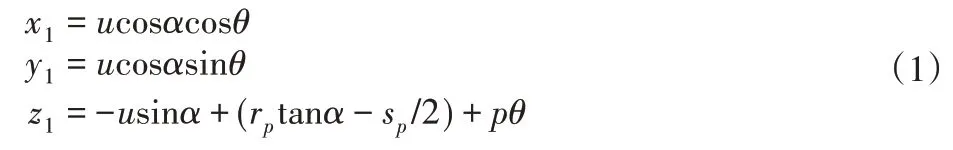
式中:α—车刀的齿形角,即蜗杆的齿形角;u—车刀刃口上点的位置参数;sp—设计参数,等于蜗杆齿槽在轴截面内的轴向宽度;rp—蜗杆的节圆半径,p—螺旋参数,p=H/2π,H—导程。
2.2 ZA蜗轮的数学模型
根据齿轮啮合原理,建立蜗杆副啮合过程的坐标系如图2所示。

图2 蜗轮蜗杆啮合坐标系Fig.2 Worm Gear Meshing Coordinate System
其中S为固定坐标系,SP为辅助的固定坐标系,S1、S2分别为蜗杆、蜗轮固接的动坐标系,蜗杆以定角速度绕z1轴回转,蜗轮以定角速度绕z2轴回转。
蜗杆副为共轭齿面,通过推导得到蜗杆副的啮合方程,与蜗杆齿面方程联立并进行坐标系转换,可以得到ZA蜗轮的齿面方程为:

式中:x1、y1、z1—接触点P在坐标系S中的坐标;x2、y2、z2—接触点P在坐标系Sp中的坐标;φ1—蜗杆在坐标系S中的转角;φ2—蜗轮在坐标系Sp中的转角;A0—中心距;i12为传动比。
3 建立ZA型蜗杆副的三维模型
通过上述对蜗杆副齿面数学方程的推导,在Matlab中对蜗杆副的齿面点进行编程求解,文中采用ZA型蜗杆副的基本参数,如表1所示。

表1 ZA蜗杆副的基本几何参数Tab.1 Basic Geometric Parameters of ZA Worm Gear
将Matlab中得到的齿面点导入UG,在UG中实现齿面的构建,并对齿面进行缝合、剪切、布尔等操作,完成对蜗杆副实体模型的建立,如图3所示。
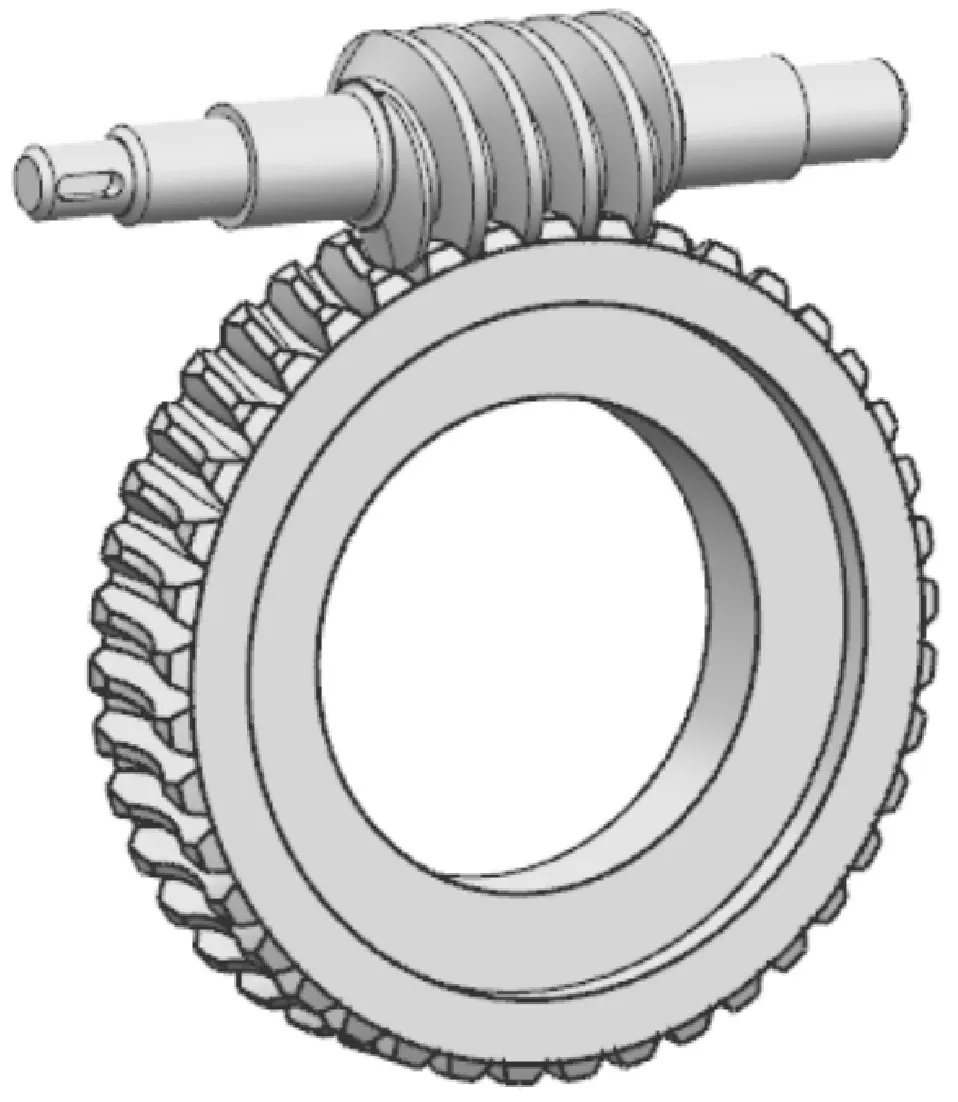
图3 ZA型蜗杆副的三维模型Fig.3 Three Dimensional Model of ZA Worm Pair
4 蜗杆副的动力学仿真分析
4.1 蜗杆副的动力学模型建立
文中采用的RecurDyn是韩国FunctionBay公司利用最新的多体动力学理论,基于相对坐标系建模和递归求解算法开发的动力学软件,可以实现快速稳定求解机构碰撞问题。
将UG中蜗杆副的装配模型以parasolid格式导入RecurDyn中,分别添加蜗杆和蜗轮与大地的旋转副,建立蜗杆齿面与蜗轮齿面的扩展面接触(Extended Surface to Surface Contact)。蜗杆上添加旋转驱动,蜗轮上添加负载转矩,完成对蜗杆副的动力学模型建立,如图4所示。

图4 ZA蜗杆副的动力学模型Fig.4 Dynamic Model of ZA Worm Pair
4.2 动力学仿真分析
根据RecurDyn的接触算法[9],对接触参数进行设置,蜗杆采用碳钢材料,弹性模量为2.06x105MPa,泊松比为0.3;蜗轮采用铸造锡青铜材料,弹性模量为8.83x104MPa,泊松比为0.3。经计算的接触刚度系数为3.63x105N/mm3/2,阻尼系数为50N·s/mm,非线性指数为1.5,最大穿透深度为0.1mm;动态摩擦系数为0.05,静态摩擦系数为0.08。蜗杆采用step阶跃函数进行驱动,在0到0.5s内加速到45rad/s,即step(time,0,0,0.5,45),蜗轮上施加一个为50N·m的转矩负载,即step(time,0,0,0.5,50000),仿真时间为3s,仿真采样步数为300步。
经上述参数设置,进行动力学仿真,蜗杆的驱动转速为45rad/s,蜗杆副的传动比为20.5,图5可以看出0到0.5s是个加速过程,0.5s后蜗轮的角速度稳定在2.20rad/s上下,与理论值2.195rad/s非常接近,验证模型建立的正确性。

图5 蜗轮输出角速度Fig.5 Worm Gear Output Angular Velocity
5 蜗杆副的传动误差分析
根据齿轮传动误差定义,当主动轮转过一定角度时,从动轮的实际转动角度与理论转动角度的差值,表达式为:

式中:φ1、φ2—主动轮和从动轮的实际转角主动轮和从动轮的初始位置;N1、N2—主动轮和从动轮的齿数。
在不同负载、转速下,对蜗杆副传动模型进行动力学仿真分析,将RecurDyn中的仿真数据导入到Matlab中,根据传动误差的公式,完成对蜗杆副的传动误差分析。
5.1 负载对传动误差的影响
将蜗杆的转速恒定为45rad/s,分别对蜗轮施加50N·m、150N·m、250N·m三种情况进行仿真分析,得到定转速变转矩的动态传动误差曲线图,分别如图6(a)、(b)、(c)所示。

图6 转速为45rad/s不同负载传动误差图Fig.6 Transmission Error Diagram for Different Loads at 45 rad/s
通过对上述三种情况进行对比分析可知,在0到0.5s初始加速阶段,蜗杆副的传动误差依次增大,0.5s后蜗杆的转速稳定,齿面传动误差呈周期性,在一定范围内上下波动。蜗杆转速稳定后,传动误差的均值随着负载的增大而增大,且负载越大传动误差的波动范围越大。根据传动误差的啮合信息可以反映出,转速恒定时,随着负载的不断增大,蜗杆副的啮合振动和噪声也在增大。
5.2 转速对传动误差的影响
将蜗轮的转矩恒定为150N·m,分别对蜗杆的驱动转速为45rad/s、65rad/s、85rad/s三种情况进行仿真分析,得到定转矩变转速的动态传动误差曲线图,分别如图7(a)、(b)、(c)所示。
通过分析定转矩变转速的传动误差图可知,在蜗轮施加恒定负载的情况下,随着蜗杆转速的增大,蜗杆副传动误差的均值和波动幅值基本一致。可以反映出蜗杆副啮合传动产生的振动和噪声,受蜗杆转速的增大影响较小。
6 结论
基于齿轮啮合原理,对ZA型蜗杆副的齿面方程进行数学模型的推导,得到ZA型蜗杆副的数学表达式。
完成对ZA型蜗杆副三维模型的建立。根据蜗杆副的数学模型,在Matlab中进行编程得到齿面点,将点云数据导入到UG中,完成蜗轮蜗杆的模型建立。
在RecurDyn中建立蜗杆副的动力学模型,验证了三维模型和动力学模型建立的正确性。通过对蜗杆副传动误差的分析,发现恒定转速情况下,负载增大对传动误差的影响明显增大;在恒定负载情况下,转速增大对传动误差影响基本一致。通过对蜗杆副传动误差的仿真对比分析,为蜗杆副的设计提供评价依据,为齿轮啮合的振动和噪声研究提供参考。
