一种用于机器人抓取的单目实时三维重建系统

吉白冰，曹其新

（上海交通大学机械与动力工程学院，上海200240）

1 引言

三维重建系统在机器人、生物医学工程、建筑测绘等领域均有广泛的应用。在机器人领域当中，三维重建主要有两类应用，一类是移动机器人的定位导航地图构建，另一类是机器人的抓取任务中，待抓取物体的三维模型构建。在机器人抓取任务中，无论是传统的PPF方法［2］还是基于深度学习的物体姿态估计方法［3］都将待抓取物体的三维模型作为已知信息。目前基于结构光原理［4-5］的三维扫描仪虽然可以重建较高精度的物体模型，但此类三维扫描仪价格昂贵且操作繁琐，在家庭环境中难以被普通用户接受和使用。视觉传感器成本低且通用性强的传感器。目前已有应用单目传感器解决工业机器人识别问题的研究［9］，基于视觉的三维重建系统，对家用服务机器人抓取任务也有很大意义。

针对基于视觉传感器的三维重建问题，文献［10］提出了一种基于运动恢复的双目视觉三维重建系统，将原有抛物线拟合的方法加入到三维重建系统，提高了三维重建系统精度。但并未考虑到双目图像错误立体匹配产生的三维结构，重建结果中噪点较多，因此上述方法仅在形状规则的物体中取得较好的效果。面向家庭环境的机器人视觉抓取的三维重建系统具有以下几个特点：一是涉及到的场景较小，一般为桌面上玩偶、书本等物体，太大或太小的物体都难于使用抓手抓取；二是重建使用的硬件和三维重建软件系统需简单易用，方便家庭用户的使用；三是对精度与实时性有一定要求。

针对上述特点，提出了一种应用于家庭环境中机器人抓取任务的单目三维重建系统，可以基于目前消费电子产品中主流的单目视觉传感器实时运行，降低了传统三维重建系统对传感器的要求。同时，在传统单目三维重建系统上增加了基于连通区域滤波器等后处理模块，用于消除立体匹配中错误恢复的三维结构，保证重建效果和精度。此外，算法基于GPU并行处理技术［11］设计和实现，加速立体匹配过程，确保三维重建系统实时性。

2 单目三维重建系统算法框架

双目三维重建系统建立在的理想双目相机成像模型下，即左右两个相机位于同一平面（光轴平行），且相机固有参数（如内参矩阵K）一致。可推出如下公式，如图1所示。

图1 理想双目模型Fig.1 Ideal Stereo Model

式中：x2-x1—视差，b—相机左右目的光心O1和O2间的距离，p1—空间点P在左相机成像的像素，p2—空间点P在左相机成像的像素。空间点P的深度Z与视差成反比，即深度图的计算与视差图的计算具有反比对应关系。

对于围绕物体运动并采集图像的单目相机而言，虽然缺少物理意义上的双目结构，但可以组合当前相机所拍摄图像与历史某时刻相机所拍摄的图像组成从运动中构造双目（motion stereo）。如图2所示，公式（1）在从运动中构成双目的相机配置下不再成立，且从运动中构造双目的相机相对位置关系未知且并不固定。因此不能简单应用双目三维重建方法解决单目三维重建问题。

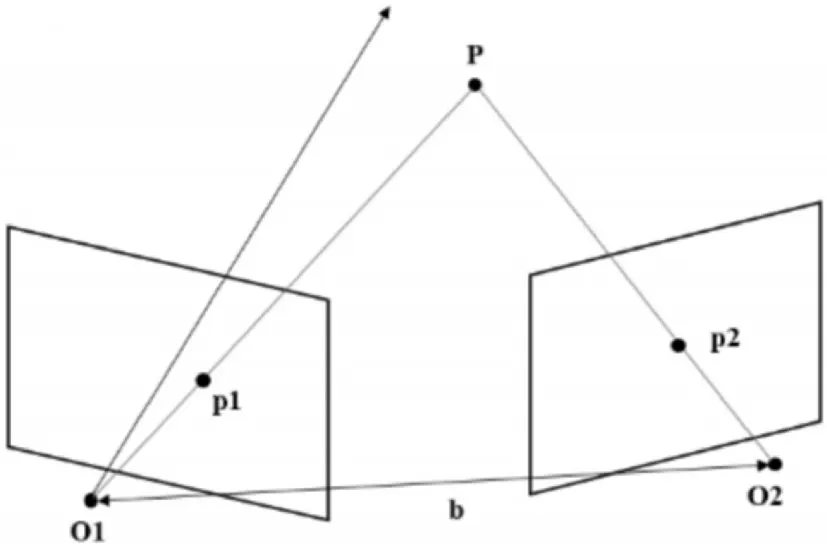
图2 从运动中构造双目的双目相机位置关系Fig.2 Motion from Stereo

针对单目三维重建问题的上述特点，提出了的三维重建系统算法框架。在单目三维重建系统中，首先根据SFM算法［7-8］恢复不同时刻相机间的相对运动关系，根据几何关系选择相机当前帧和过去某一帧组成虚拟双目。根据虚拟双目间的几何关系和图像像素相似性，计算当前帧视场内的场景点云。经过坐标系变换将不同时刻相机帧重建点云拼接为完整的物体模型。系统基于SFM算法恢复相机运动，后应用TSDF方法［6］完成坐标系对齐功能。上述方法已有成熟的研究结果，因此不再赘述相应原理。下文中将详细说明基于虚拟双目构造、立体匹配及后处理过程，如图3所示。

图3 算法流程图Fig.3 Flow Chart of Proposed Algorithm

3 单目三维重建系统的三维结构恢复

在单目三维重建系统中，三维结构恢复指根据从运动中构造的双目计算相机视场内的场景三维结构。下面将从虚拟双目构造，虚拟双目立体匹配，后处理三个部分介绍基于单目相机的三维结构恢复方法。

3.1 虚拟双目构造

基于SFM方法恢复的相机相对位置关系存在一定误差，因此要保证最终场景三维结构的准确性，需要合理选择历史相机帧与当前帧配对，使得误差对深度图质量的影响较小。在配对选择的过程中，历史相机帧与当前相机帧间要保持较大的重叠和相似的朝向，这样深度图可以覆盖图像的大部分范围，同时两个相机状态间要有合理的基线，较长的基线会降低图像的重叠度，减少深度图的有效区域，较短的基线会导致深度图易受到噪声的干扰，降低深度估计的准确性。基于上述分析，提出了如下评价函数：

3.2 虚拟双目的立体匹配

由章2所述，从运动中恢复双目得到双目图像对基本不满足理想双目模型，因此其立体匹配过程分为如下几步：

像素匹配和匹配代价计算：首先基于先验信息确定待计算深度图的图像所对应场景的深度分布区间，在得到的分布区间内确定N个深度假设，每个深度假设对应于一个代表深度值d的平面。为增强深度估计结果对于场景光照变化和图像噪声的鲁棒性，在以像素p为中心的方形领域内采样计算代价函数C（p，d）。应用ZNCC算子构造像素对应代价函数C（p，d）。

式中：q—右图像中与像素p对应的像素，K—内参矩阵，R—相机旋转矩阵，t—相机平移向量，n—平面法向量。q代表像素p在由图像上的投影，如图4所示。

图4 像素点投影示意图Fig.4 Illustration of Pixel Reprojection

代价聚合与深度值求精：计算得到每个深度假设d所对应的代价函数C(p,d)后，按WTA规则估计每个像素p所对应的深度：

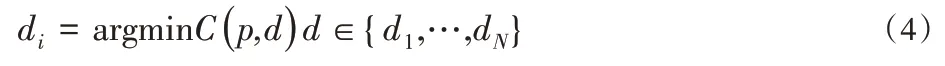
为补偿深度假设离散化造成的精度损失，采用抛物线拟合的方式获取亚像素级深度估计精度。则抛物线函数极小值点对应的深度值dmin满足公式（5）：

式中：di—最小C(p,d)所对应的深度假设，di-1di+1—与di相邻的深度假设，Δd—深度假设间距。由于间中每个像素的深度估计过程具有独立性，因此每个像素的深度估计过程可以并行进行，得到初始深度图。

3.3 后处理

立体匹配计算的深度图中存在大量错误深度估计，使最终的三维模型产生大量噪点，降低三维模型质量。为解决这一问题，提出了如下的后处理过程。

左右一致性检查：由于立体匹配过程具有计算对称性，因此估计正确的深度应满足如下所示的重投影误差公式：

式中：Dc—当前帧深度图，Dk—历史帧深度图，δ—阈值，其余符号同公式（3）。

独特性比率滤波器：在被图像噪声干扰或相对运动关系的误差而产生错误深度估计的区域，其最小代价函数与次小代价函数会比较接近。根据上述观察，定义如下独特性比率过滤噪声。当像素p的独特性比率小于阈值时过滤对应深度：

式中：runiq(p)—p像素的独特性比率，dsec—次小代价函数对应的深度假设，dmin—最小代价函数对应的深度假设。rthres—独特性比率的阈值。

连通区域滤波器：真实场景中大部分区域在空间是连续的，因此体现在深度图上相邻区域的深度值也具有一定的连续性。错误匹配的深度值一般与其周边区域的深度值相比具有较大的不连续性，且在深度图中零散的分布与各个区域。根据如下公式判断深度图上某像素与相邻区域在深度图上的连续性关系。

式中：d—某像素对应深度，dr某像素领域的对应深度，Δd—深度假设间距。应用上述公式将深度图的深度连续区域的划分问题转化为一个二值图像连通区域标记问题，使用两步法将所有的深度图连通区域分类并标记。根据标记的连通区域中像素的数量，将像素数量小于一定值的连通区域从原始深度图中去除。经过上述后处理后得到的深度图经过坐标系对齐后得到最终的物体模型。

4 实验

在家庭环境中常用且易于机器人抓取的三种物体上进行了实验。实验图像分辨率为640×480，程序运行于配备i7-4710MQ处理器和GTX880M显卡的笔记本电脑上。以Realsense SR300传感器测量的结果作为真值。

对比了应用后处理和不应用后处理方法的重建结果。在实际环境中由于采集的图像中图像噪声及场景光照变化，一些在理想条件下正确匹配的像素在噪声干扰下匹配错误，进而物体模型表面不完整且中存在大量噪点。通过节3.3介绍的后处理流程可以过滤单帧深度图中的错误匹配结果。在基于运动的单目三维重建系统中，不同帧图像恢复的三维结构存在一定冗余，某一帧中被过滤的错误三维结构会被其他帧中正确估计的三维结构代替，因此后处理模块不会对完整性造成影响，如图5所示。

图5 实验结果对比Fig.5 Comparison of Experiment Result

基于结构光传感器的测量结果作为真值计算三维重建结果物体模型的精度。根据计算结果绘制了误差色温图，误差表示范围从0%到100%，且色温越冷代表误差越小。上述三个实验物体的模型与结构光传感器测量真值的中位数相对误差（MAE）均在1.0%左右，从相对误差色温图中也可以看出重建物体模型的大部分区域误差非常小。对于长宽高在20cm范围内的家庭中常见物体而言，生成的模型可以满足服务机器人构建抓取物体数据库的模型精度要求，如图6所示。

图6 三种不同物体重建模型（上）与误差色温图（下）Fig.6 Models of Three different objects 3D Reconstruction（Up）and Corresponding Error Color Map（Down）

为验证三维重建系统实时性，记录了图6中玩偶熊模型建模过程中每一帧的处理时间并绘制了的处理时间随拍摄时间变化的曲线。帧平均处理时间为33.95ms，即29.45帧/秒的处理速度，满足实时运行的要求，如图7所示。

图7 三维重建系统单帧处理时间曲线图Fig.7 Graph of Running Time of 3D Reconstruction

5 结论

介绍了一种基于运动恢复深度的单目实时三维重建系统，针对运动中单目相机采集的图像序列，提出了一种虚拟双目相机的构造准则。并推导了虚拟双目相机的立体匹配公式。针对实际场景中图像噪声对三维重建结果产生较大影响的问题，在传统算法框架基础上增加了后处理模块。实验结果表明应用后处理模块，取得了质量更好的物体模型。针对三种不同物体的重建实验说明了应用三维重建系统的精度。系统并行处理图像数据并生成三维模型。平均处理速度为29.45帧每秒，满足服务机器人抓取任务对建模系统速度的要求。未来将在本文实验得到的模型基础上，设计基于物体模型服务机器人抓取系统，进一步验证本文模型对于服务机器人抓取任务的适用性。