谐波减速器传动机构的动态仿真研究

王 祥，肖曙红

（广东工业大学机电工程学院，广东 广州510006）

1 引言

谐波传动是依靠波发生器运动迫使柔性轮发生变形，然后与刚性轮进行啮合并传递力矩，从而达到传动目的。由于谐波减速器的体积小、重量轻、传动比大和传动精度高等诸多优点，目前已经被普遍的应用在不同的机械领域当中［1］。美国的Boeing、通用汽车等多个公司针对谐波传动技术都设置了专门的研究机构，同时还有MIT和空间技术实验室等科研机构和研究中心对此技术进行相关的研究。日本建立了哈默纳科公司，并到目前为止一直都是谐波减速器领域的领导者。谐波传动技术传入国内以后就得到了国家的大力支持，学者沈允文较早的开始进行研究并发表诸多著作，近年来哈尔滨工业大学、重庆大学等高校也都进行了大量的研究工作，他们所取得的成果极大的推动了国内谐波传动技术的发展。另有以中技克美为代表的众多公司能够自主研究开发谐波减速器，他们所生产的产品也都被国内外所采用。

在谐波减速器的动力传输过程中，柔轮是核心部件。由于其是弹性薄壁零件，并且在运转过程中受到波发生器带来的交变载荷的作用下，容易对柔轮造成疲劳损坏，其中最常见的现象就是齿根的疲劳断裂。因此，柔轮的强度分析对于谐波传动来说是十分必要的，通过对柔轮进行有限元分析来为强度分析提供依据。

柔轮在谐波传动的过程中会发生弹性变形，然后与刚轮轮齿啮合，接触情况比较复杂，并且谐波减速器的模型属于刚柔混合模型，所以可以考虑在Adams中建立刚柔耦合的虚拟样机，然后对虚拟样机进行动态仿真，通过仿真分析来模拟实际运动过程中柔轮的变形以及和刚轮的啮合状态，分析在这种情况下柔轮的变形情况。

2 谐波减速器齿轮齿形设计

谐波减速器的刚轮和柔轮的齿形均采用双圆弧齿廓，采用双圆弧齿廓的齿轮在啮合的时候可以增加啮合的轮齿对数，并改善普通齿轮啮合时易产生尖点和干涉的情况，也有利于提高谐波减速器在传动过程中的啮合性能。根据双圆弧齿形的啮合原理以及传动特性，可以确定柔轮的齿廓参数如下［2］：

表1 柔轮齿廓参数表Tab.1 Tooth Profile Parameter

对所设计的柔轮齿廓建立方程组，然后进行坐标变换，并利用包络法得到对应的刚轮的齿廓方程，由于刚轮齿廓方程组中的变量参数之间是隐函数的关系，只能通过数值法进行求解［3］，所以利用Matlab对刚轮的齿廓方程进行编程，然后将相应的参数代入，拟合得到刚轮齿廓的曲线如图1所示，通过曲线可以确定刚轮齿廓曲线的半径和圆心，进一步可以求解齿廓参数，如表2所示。

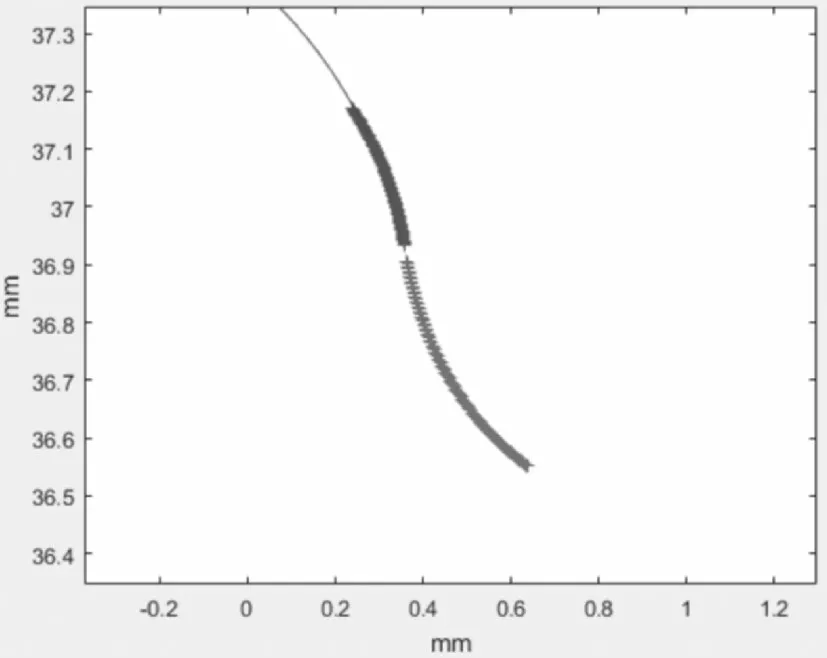
图1 刚轮齿廓曲线拟合图Fig.1 Tooth Profile Curve Fitting of Rigid Wheel

表2 刚轮齿廓参数表Tab.2 Rigid Wheel Profile Parameter

利用柔轮和刚轮的齿廓参数建立实体模型，而波发生器则采用椭圆凸轮结构，它的优点是能够平稳运转而且精度较高，柔轮和刚轮在啮合的过程中能够达到较为理想的啮合状态。

3 柔轮的接触应力分析

空载时，由于凸轮波发生器的长轴略大于柔轮的直径，因此将波发生器装入柔轮后会使得柔轮的前端面形状变为椭圆形，如图所示为按w=w0cos2φ规律变形以后柔轮的端面形状。

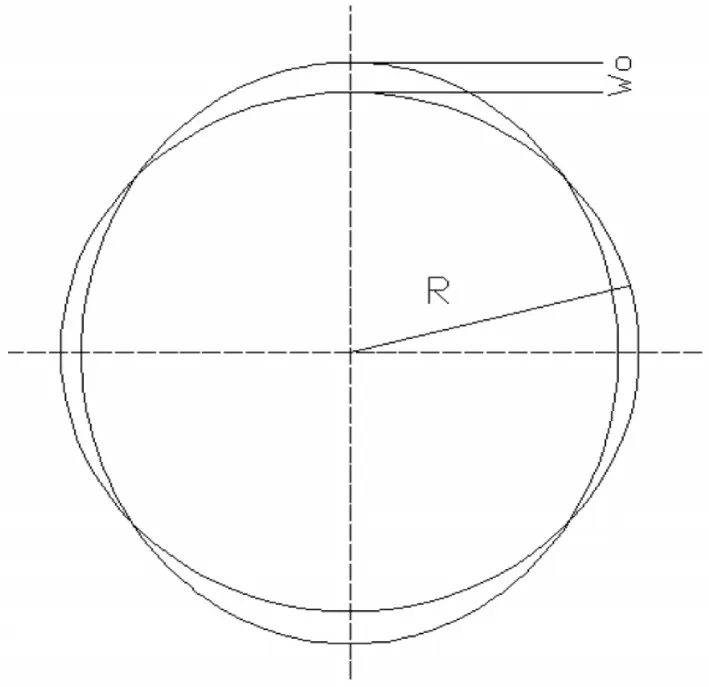
图2 柔轮按w=w0cos2φ规律变形Fig.2 Flexspline Strain of w=w0cos2φ

根据它的变形规律可以得出位移方程（

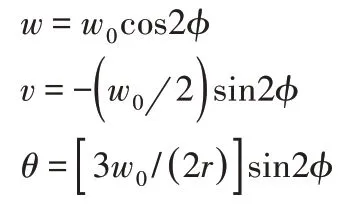
式中：w0-径向变形量系数，φ-转动角，θ-法向转角，r-柔轮半径；

由于柔轮在波发生器的作用下要发生变形，而且在和刚轮啮合的时候，接触的轮齿对数以及接触区域都不确定，因此难以准确求解柔轮的应力情况。考虑将柔轮进行简化，把它看作成一个光滑的圆柱壳体，然后利用圆柱壳体理论对柔轮进行应力分析［4］。

弯曲应力和剪切应力为：

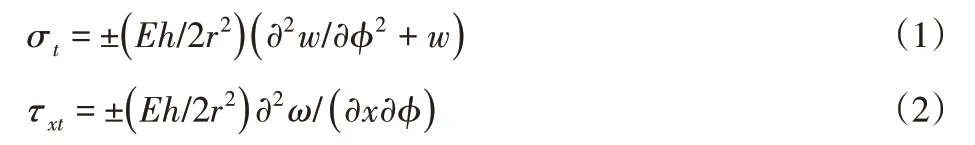
式中：E—弹性模量，h—柔轮齿圈厚度；

将柔轮的变形规律方程w=w0cos2φ分别代入式（1）和式（2），可以得到：

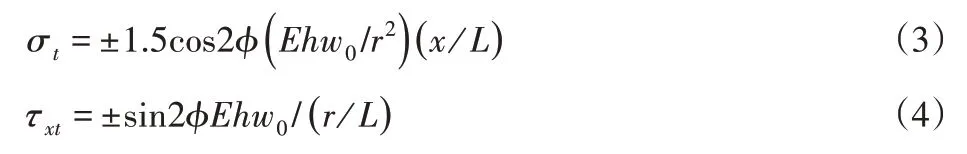
通过上述的计算公式可以看出，当柔轮的结构确定之后就可以求出柔轮的应力大小，其中柔轮齿圈的厚度h，柔轮筒长L以及柔轮的半径r对于柔轮的应力影响较大。

4 柔轮有限元接触分析

4.1 边界条件的设置

对于谐波减速器的有限元分析应该采用非线性大变形分析方法，利用Ansys Workbench对柔轮进行接触分析来模拟波发生器对柔轮的强制位移效果，分析柔轮应力应变的分布状况。

首先忽略柔轮的螺纹孔并且将波发生器和柔性轴承简化为一个外径与柔性轴承工作状态下相当外径的椭圆体，然后对柔轮模型进行适当的分割。将柔轮的齿圈和柔轮筒体进行切割分离，这样做的好处是能够保证在齿圈上能够得到相对密集的网格，而在筒体上可以得到相对稀疏的网格［5］。

对模型进行接触条件的设置，将柔轮内表面设置为目标面，波发生器外表面为接触面，接触系数0.08，添加偏移量，数值为0，接触计算方法为加强的拉格朗日法，接触刚度定义为手动控制，刚度值为0.01，柔轮和刚轮之间的接触设置同上，将摩擦系数设置为0.12，由于柔轮会发生较大变形，因此开启大变形选项。

由实际情况考虑，约束波发生器的轴向位移，采用（Remote displacement）限制Y轴方向的位移；因为刚轮是固定在机构的壳体上，所以约束刚轮外表面的所有自由度（Fixed support）。

4.2 分析结果

从图3（a）中可以看出，应力沿着Z轴方向从齿圈处向筒底方向逐渐减小，在波发生器的作用下，柔轮前端面由圆形变为椭圆形，并在柔轮的内壁、波发生器的长轴和短轴位置处产生拉应力和压应力。应力最大的地方发生在柔轮齿圈和筒体过渡的齿根处，应力大小为409.6MPa，这是因为柔轮发生变形使这个位置产生了应力集中现象。大长径比使得柔轮筒体较长，因而柔轮在受力的过程中筒底处受力较为均匀，所以在筒底几乎没有应力的存在。

图3 柔轮分析结果Fig.3 Analysis Result of Flexible Wheel

由（b）可以看得出，柔轮的变形量也是沿着Z轴向筒体方向逐渐减小，在筒底的位置变形量为0，而变形量最大的地方发生在齿圈前沿与波发生器的长短轴的位置，变形量为0.68558mm，这是由于波发生器的初始载荷使得柔轮前端面在波发生器的长短轴位置处发生变形，并影响柔轮筒体，之后沿着筒体的方向影响在逐渐减小。柔轮的变形对于谐波减速器的使用寿命以及传动的稳定性来说都有很大的影响，因此应尽量保证柔轮在工作的过程中不发生较大的变形。

5 柔轮工作过程的动态仿真

在谐波减速器的实际运动过程中，波发生器的转动会导致柔轮转动并且产生变形，而在与刚轮的啮合过程中，由于受到刚轮轮齿的约束且啮合区域不断变化的情况，会导致柔轮的运动状态和啮合状态变得比较复杂［6］。因此考虑在Adams中建立谐波减速器的刚柔耦合虚拟样机，之后对虚拟样机进行动态仿真，求解柔轮在负载情况下的运动状态，同时验证模型是否合理。

5.1 虚拟样机的建立

利用Abaqus建立柔性体模型，首先将装配体模型导入到Abaqus里，定义材料和属性并划分网格，然后创建模态分析步和设置所需要输出的模态特征值。之后在柔轮的前端口和后端口的中心点的位置建立RP点并添加RP点与模型之间的MPC Constrain，对所建立的RP点进行自由度约束。建立Job并修改模型的关键语句后提交分析会得到模型的模态分析结果，之后打开Abaqus的命令流进行相关修改后即可得到生成的mnf文件。在Adams中打开装配体模型，用mnf文件替换刚性体柔轮，即得到谐波减速器的刚柔耦合模型［7］，如图4所示，此时的柔轮已经变为柔性体。对模型赋予零件密度、泊松比以及杨氏模量等参数值，同时Adams将会自动计算出各个零件的质量和转动惯量等参数［8］。

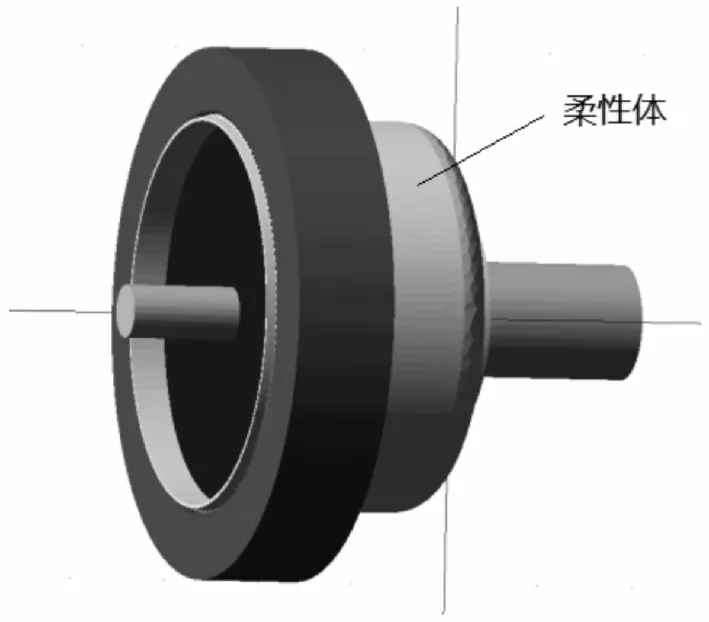
图4 谐波传动虚拟样机模型Fig.4 Harmonic Drive Virtual Prototype Model

5.2 施加载荷和约束

在谐波传动的过程中，刚轮是固定不动的，所以在刚轮和大地之间施加固定副，同时对输入轴和波发生器以及柔轮和输出轴之间添加固定副；而在输入轴和大地以及柔轮和大地之间建立旋转副；对输入轴添加驱动，输入轴的转速为600r/min( )3600°/s，为了能够保证平稳的启动运转，利用STEP函数来调节驱动的转速［9］（Step(time,0,0d,0.03,3600d)。

对模型进行仿真参数的设置，为了能够得到收敛以及正确的仿真结果，设置仿真的时间为0.5s，仿真的步数为300进行仿真。

5.3 仿真结果

5.3.1 谐波传动装置的运动

后处理查看仿真结果可得波发生器和柔轮的转速，如图5～图6所示。

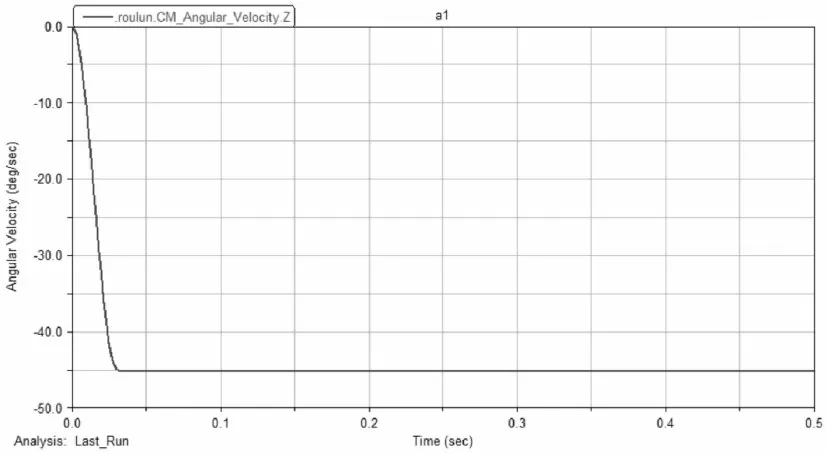
图6 柔轮转速Fig.6 Speed of Flexible Wheel

由图5和6中可以看出，波发生器和柔轮的转动方向是相反的，这与实际的谐波减速器的工作情况相吻合。通过分析曲线可知，在0-0.03s中，电机的转速在逐渐增加，因而波发生器和柔轮等各部件的转速也开始相应的增加。之后柔轮开始逐渐趋于稳定的啮合状态，在0.03s之后转速值稳定在45°/s，此后的谐波建减速器处于负载匀速的运动过程。由波发生器和柔轮的转速可知，谐波传动装置满足传动比80的设计要求，谐波传动装置的各部件设计也合理。

图5 波发生器转速Fig.5 Speed of Wave Generator

下图分别为波发生器和柔轮的角加速度变化曲线，通过曲线可以看出波发生器和柔轮的加速度方向相反，在0-0.03s之间是处于加速过程，大约在0.015s的时候加速度达到最大值，而在0.03s之后加速度为0，说明此时的柔轮和波发生器均处于匀速运动的阶段，这也与开始设定的驱动转速相吻合，如图7～图8所示。

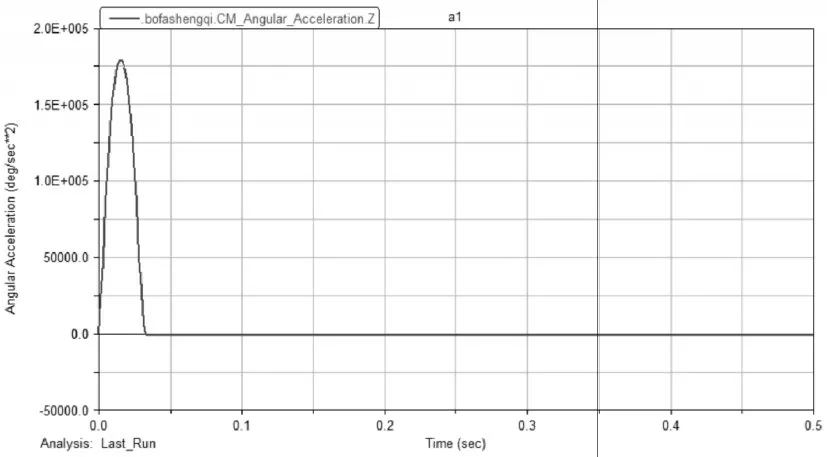
图7 波发生器角加速度Fig.7 Angular Acceleration of Wave Generator

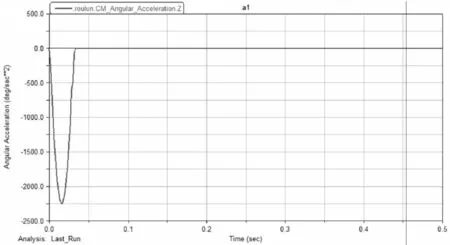
图8 柔轮角加速度Fig.8 Angular Acceleration of Flexible Wheel

5.3.2 谐波传动装置的啮合状态

从仿真结果图9可以看到，波发生器使柔轮产生了变形，同时在刚轮的作用下，柔轮向着波发生器的反方向转动。柔轮和刚轮的啮合点发生在波发生器的长轴两端，该位置处的柔轮轮齿和刚轮轮齿完全啮合。轮齿沿着椭圆两侧向短轴方向逐渐脱离啮合，在短轴处则处于完全脱离啮合的状态。在工作状态下，柔轮的轮齿依次顺时针的经过波发生的长轴，并且每经过四分之一周之后，位于长轴方向上的轮齿将会到达柔轮波发生器的短轴方向。波发生器每顺时针转过一周，柔轮将会逆时针的转过刚轮的两个齿，并且和刚轮产生啮合，从而实现了从高速到低速的二齿差减速效果。

图9 柔轮刚轮啮合模拟Fig.9 Meshing Simulation of Flexible Wheel Rigid Wheel

6 结论

通过对柔轮进行有限元接触分析可以得到柔轮的应力分布均匀，对所建立的刚柔耦合模型进行动态仿真可以得到运动过程中柔轮的变形情况以及柔轮和刚轮轮齿间的动态啮合过程，由曲线可知谐波减速器的输出转速满足传动比的设计要求，同时柔轮和刚轮轮齿之间的啮合传动过程平稳，所以可以说明虚拟样机的模型建立正确，为后续的疲劳分析提供基础。